Φ114.3 mm×8.56 mm 140V 套管抗外挤能力研究

许雷明，高连新，戴涵洋，张 恒

（1.江苏常宝普莱森钢管有限公司，江苏 常州 213200；2.华东理工大学机械与动力工程学院，上海 200237；3.江苏常宝股份钢管有限公司，江苏 常州 213000）

抗挤强度是套管使用性能的一项重要指标，早在20 世纪30 年代，美国石油协会（API）便开始组织研究套管的抗挤强度问题。根据研究结果，API于1968 年9 月给出了计算套管抗挤毁强度的4 个公式。这4 个公式依据套管外径与壁厚之比D/t的范围，分别对应于屈服挤毁、塑性挤毁、过渡挤毁及弹性挤毁4 种失效形式［1］。计算套管抗挤强度时，先依据其D/t值确定失效形式，再对应不同的计算公式。4 个公式，有的是经过简化处理的理论公式，有的是试验统计得到的经验公式，它们都没有考虑套管残余应力、几何缺陷（如不圆度、壁厚不均度）等的影响［2-3］，自发布以来也没做过任何修正，导致利用这些公式计算的套管抗挤强度与实际值相比有较大误差，特别是高抗挤套管的误差更大［4-5］。因此，如何计算套管特别是高抗挤套管真实的抗挤强度是目前仍未解决的技术难题［6-8］。

以Φ114.3 mm×8.56 mm 140V 套管为对象，通过试验和数值模拟的方法，研究了该类型套管的抗挤强度及在挤毁失效过程中的变形情况，分析了材料强度、壁厚不均度和椭圆度等对抗挤性能的影响。全面系统地分析Φ114.3 mm×8.56 mm 140V 套管抗挤强度的大小及影响因素，有助于认识套管挤毁失效的机理，为开发高抗挤套管提供参考。

1 试验方案

选用Φ114.3 mm×8.56 mm 140V 套管10 支，将10 支样管按立式套管复合挤毁试验系统要求的长度取样，样管长度950～955 mm，编号1～10，端面斜度/平面度≤±1.5 mm，要求端面无毛刺、油脂，内壁打磨清理无异物。

试验前进行样管壁厚、外径等几何尺寸的检测。将每支样管沿轴向每间隔8 cm 设置一个测量截面，每个截面分为4 个象限。划线后，使用手持测厚仪和外径千分尺测量每个截面上4 个点的外径和壁厚，由于测量数据较多，为方便起见，仅测量对抗挤强度计算及有限元建模有影响的最小、最大、平均壁厚，以及最小、最大、平均外径。

2 挤毁试验结果

10 支试样的外径、壁厚检测划线情况如图1所示。利用无附加载荷的套管复合挤毁试验系统［9］进行外压挤毁试验，加压介质为清水。与传统的封堵管端加压的方式相比，该试验系统不会产生附加轴向载荷，也不会受焊接堵头增强作用的影响，因而更能有效地模拟实际工况，数据更加准确。10支管子的尺寸测量结果及试验结果见表1。

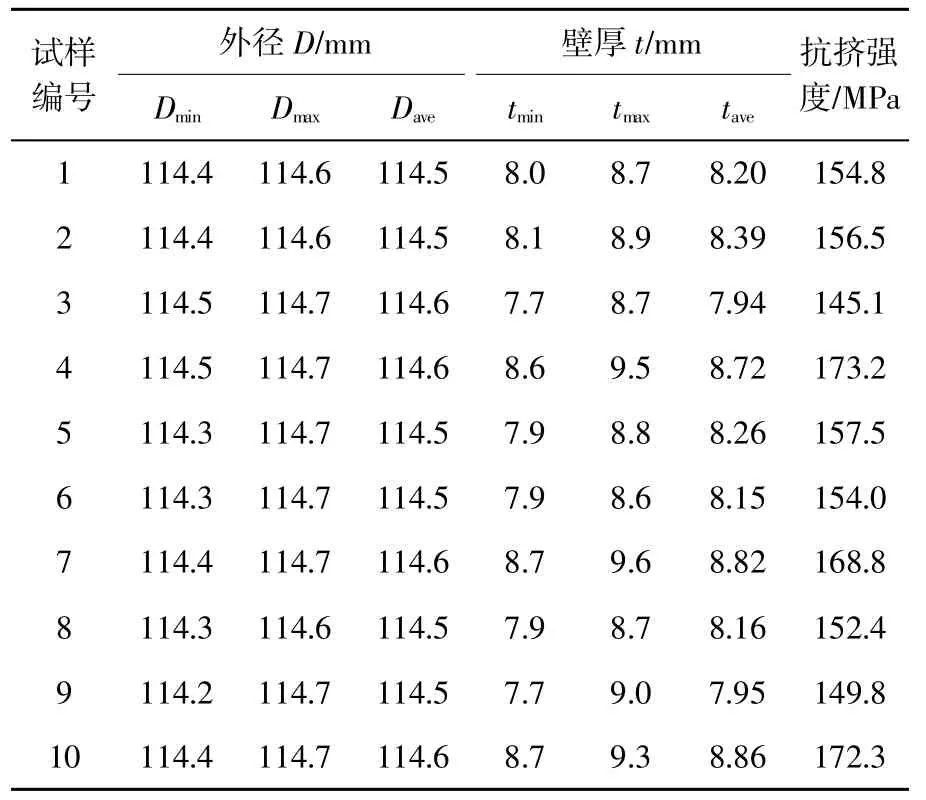
表1 140V 样管几何参数及挤毁试验结果

图1 140V 套管挤毁试验样品

从表1 及图1 可知，尽管这10 支套管属于同一厂家生产的同材质、同钢级、同规格、同批次的产品，但抗挤强度却有较大差别，抗挤强度最高的4 号试样比最低的3 号试样高了19.4%。这说明在材料性能相同的情况下，轧制工艺造成的几何缺陷对套管的抗挤性能有重大影响，故目前利用API 计算公式代入名义外径和名义壁厚来预测套管抗挤强度的办法并不可靠。

进一步结合套管的实测壁厚和外径可见，这批套管外径较均匀，最大外径只比最小外径大了0.5 mm，但壁厚不均度较大，最大壁厚比最小壁厚大了1.9 mm。在其他条件相同的情况下，可以初步断定，这批套管抗挤强度不同的原因主要是由壁厚不均和外径椭圆引起的。进一步观察试样失效后的形貌，可知变形最大的位置与最小壁厚所在位置是对应的，但与椭圆度没有明显对应关系。

3 抗外挤能力的理论计算

3.1 名义参数下的抗挤强度

根据ASTM A 370—2018《钢制品力学性能试验的标准试验方法和定义》，试验前在管体上截取板状拉伸试样，测量钢管材料的机械性能，结果为：屈服强度Yp=1 081 MPa，抗拉强度Yb=1 122 MPa，伸长率δ=21%。因为这10 支管子均来自同一个热处理批次，机械性能基本相同，因此只取其中一支进行了机械性能试验。

对于Φ114.3 mm×8.56 mm 140V 套管，在名义尺寸下，D/t为13.35，根据API TR 5C3—2018《套管、管道和用作套管或管道的线管的等式和计算技术报告》，在140V 钢级情况下，套管的挤毁模式属于塑性挤毁，其塑性抗挤强度Pp为：

式中A，B，C——系数。

API 公式均适用于英制单位，将名义屈服强度Yp=140 000 psi 代入A、B、C表达式，可得A=3.297，B=0.097 1，C=375 1，再进一步代入挤毁强度计算公式，可得Pp=17 223 psi，换算成公制单位，Pp=118.8 MPa。

3.2 实测参数下的抗挤强度

根据API TR 5C3，当D/t≤（D/t）YP，套管的挤毁失效模式是屈服挤毁；当，套管的挤毁失效模式是塑性挤毁；当（D/t）TE，套管的挤毁失效模式是过渡挤毁；当，套管的挤毁失效模式是弹性挤毁。其中：

式中（D/t）YP——界定屈服挤毁模式或塑性挤毁模式的D/t临界值；

（D/t）PT——界定塑性挤毁模式或过渡挤毁模式的D/t临界值；

（D/t）TE——界定过渡挤毁模式或弹性挤毁的D/t临界值；

F，G——系数。

将10 支样管的实测屈服强度Yp=1 081 MPa，换算成英制单位后代入公式（2）～（4）和（8）～（9），计算出系数A、B、C、F和G，并代入公式（5）～（7），求得径壁比的临界值（D/t）YP、（D/t）PT分别为11.567 和18.306。利用10 支样管的实测平均壁厚t、实测平均外径D（表1），进一步得到D/t后，与径壁比的临界值比较，判断套管的挤毁失效模式。对比发现，10 个样品的D/t在11.567～18.306，因此属于塑性挤毁。利用公式（1）即可得到10 支样管的抗挤强度值，计算结果见表2，名义参数（名义壁厚、名义外径）下的抗挤强度为118.8 MPa。

表2 140V 样管实测参数下的抗挤强度结果

4 抗外挤能力的有限元模拟

上述理论计算公式只涉及套管材料的屈服强度而未涉及抗拉强度，其计算依据是套管内壁屈服强度。有限元法则不仅考虑了材料的屈服强度，而且考虑了屈服后的硬化，因而与实际更接近。实际上，内壁屈服时套管并未破坏，如果按照上述公式预测抗挤强度，往往会造成套管材料浪费或套管选择困难［10-11］，利用有限元法可以有效避免这一问题。

4.1 模型及网格划分

采用有限元法计算套管的抗挤强度，结果的准确性取决于所建的模型以及边界条件。根据套管在复合挤毁试验系统中的受力特点（无附加轴向载荷、无弯曲载荷、受均匀外压），并假设套管各截面的不圆度和壁厚不均度相同，分析模型可按平面应变问题处理，即只需对套管的一个截面进行有限元建模。同时，考虑到套管挤毁失效变形很大，材料超出了弹性范围，因此建模时还要考虑材料、几何尺寸等非线性问题。

采用表1 中的数据建立模型。以1 号试样为例，外壁长轴114.6 mm，设在X轴上；短轴114.4 mm，设在Y轴上；长轴处的壁厚8.7 mm，短轴处的壁厚8.0 mm。同时以实测屈服强度、抗拉强度为模型材料参数。在套管外壁施加均匀外压，为消除刚体位移引起的刚度矩阵奇异性，在模型上施加位移约束，但这种约束会提高模型刚度，对失效模式产生影响。在X轴上的a点约束Y方向位移，在Y轴上的b点约束X方向位移，这样设置可减小附加约束的影响。设置单元类型为CPE4R（四节点四边形双线性减缩积分平面应变单元），利用Abaqus 有限元软件建立如图2 所示的模型。

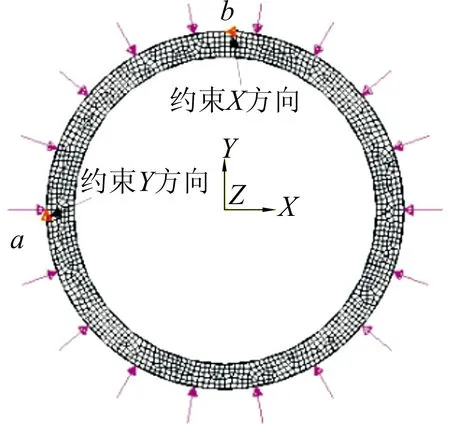
图2 140V 样管有限元模型及网格划分

4.2 计算结果

研究套管在外压作用下的挤毁失效过程，随着外压的增大，图2 中a点沿X方向、b点沿Y方向的位移以及a点和b点的环向应变如图3 所示。

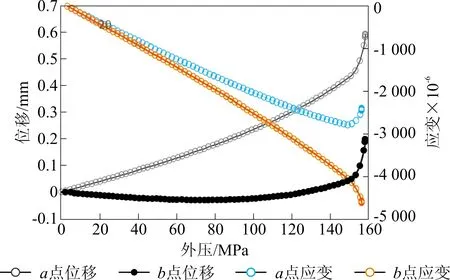
图3 140V 样管挤毁过程中外壁的变形和应变

从图3 可见，壁厚最厚的a点，在整个加压过程中一直沿X轴向右移动；而壁厚最薄的b点，随着外压增大先是沿Y轴向下移动，表现出收缩的趋势，当外压增大到80 MPa 后，又沿Y轴向上移动，直至突然失稳失效，失效时外压156 MPa。最后失效的有限元模型形貌和实际失效样管形貌如图4 所示，二者完全吻合。

图4 140V 样管失效试验模型示意

从图3 可见，在外压至失效过程中，a、b两点的环向应变均为负值，说明处于受压缩状态；在外压达到150 MPa 以前，应变和外压呈明显的线性关系，说明套管处于弹性变形范围；当外压超过150 MPa 后，应变随外压增大而急剧变化，直至到156 MPa 失效。可见，不论是失效模式，还是失效外压值，有限元结果与试验结果都吻合，说明建立的有限元模型是合理的。利用同样的建模方法，建立其余9 支样管的有限元模型，计算挤毁失效载荷结果见表3，有限元值、理论计算值和试验值对比曲线如图5 所示。

表3 140V 样管有限元模拟挤毁失效载荷结果及对比

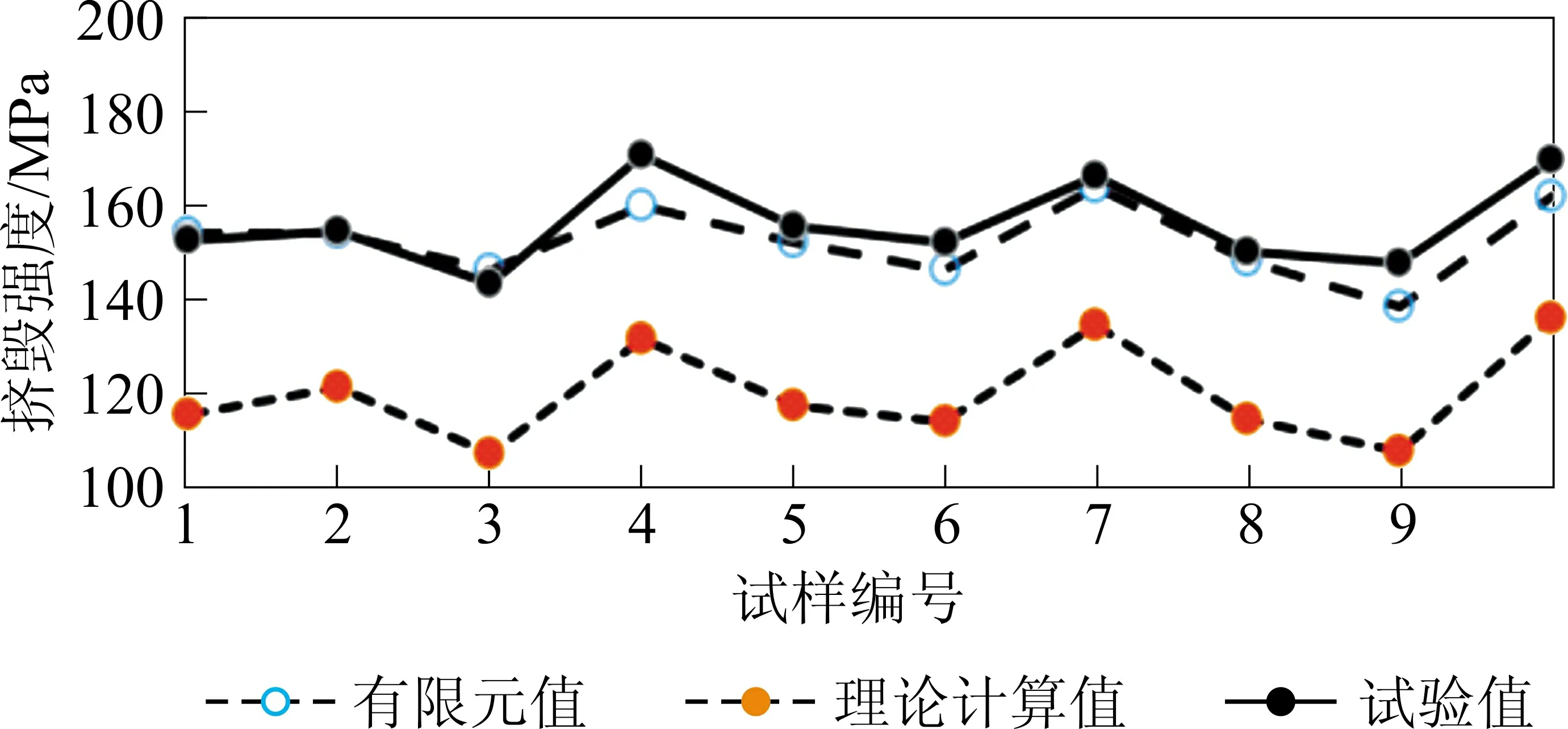
图5 140V 样管有限元模拟挤毁失效载荷数据对比

从表3 和图5 可见，有限元模拟值与试验值非常接近，偏差在-0.77%～+7.00%；理论计算值与试验值偏差较大，偏差在23.84%～37.56%。这说明用建立的有限元模型计算套管的抗挤强度，比API公式具有更高的精度，建模方法切实可行。

5 壁厚不均度和椭圆度对套管抗挤性能影响

（1）壁厚不均度。壁厚不均一般是由于轧管时偏心造成的，这种情况下平均壁厚相等。建模时以1 号试样的最大、最小外径为基准，最大壁厚设置在长轴，最小壁厚设置在短轴。分析不同情况时的抗挤强度，计算结果见表4 和图6。

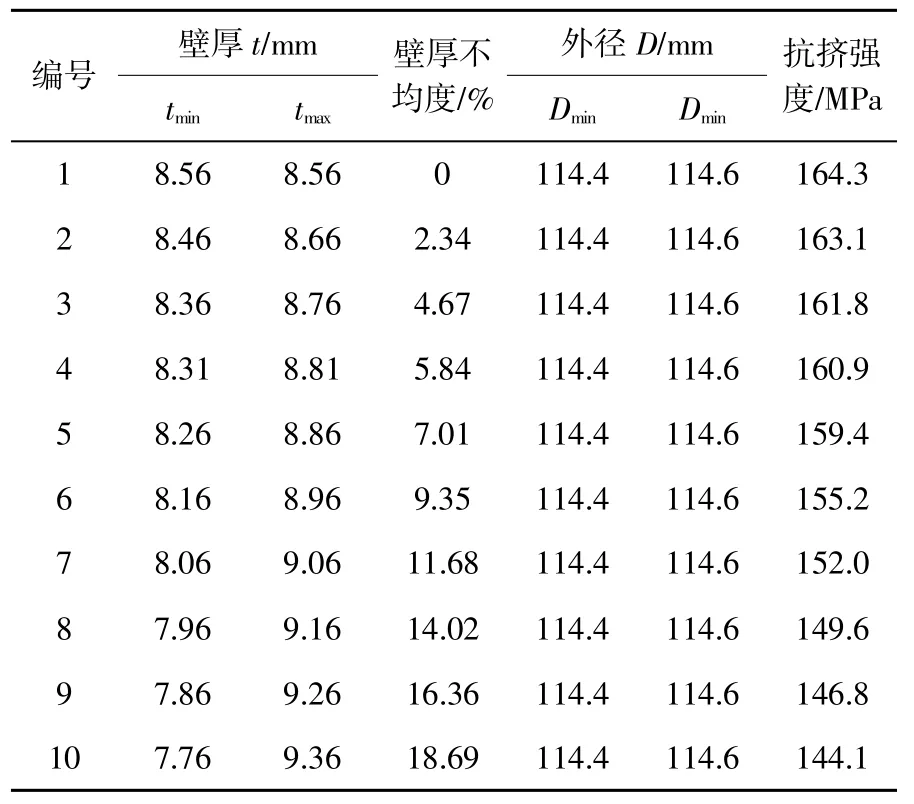
表4 140V 套管壁厚不均度和抗挤强度有限元结果

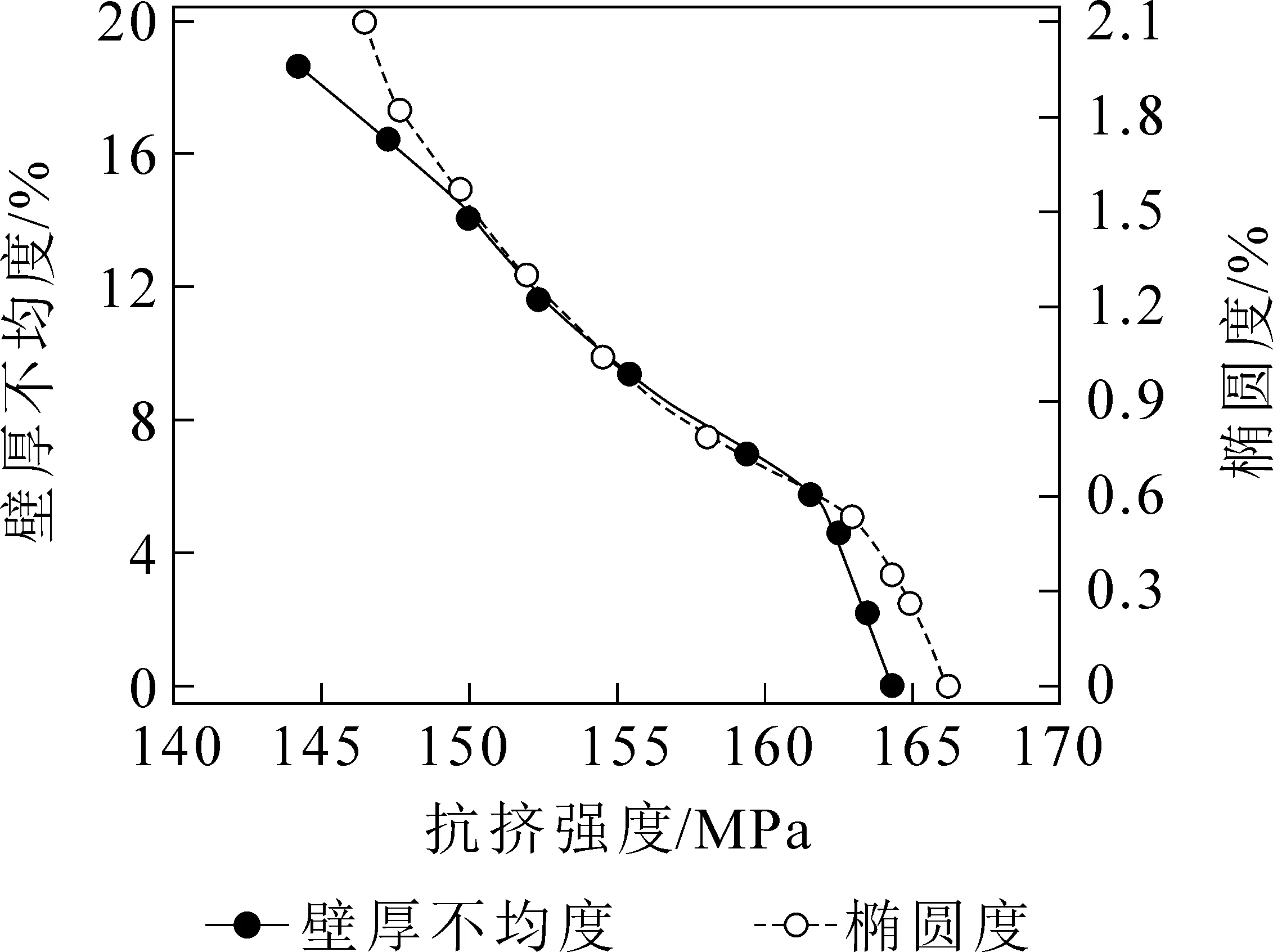
图6 140V 样管壁厚不均度和椭圆度与抗挤强度的关系

（2）椭圆度。保持壁厚不变，模拟不同椭圆度情况下套管的抗挤强度，结果见表5 和图6。

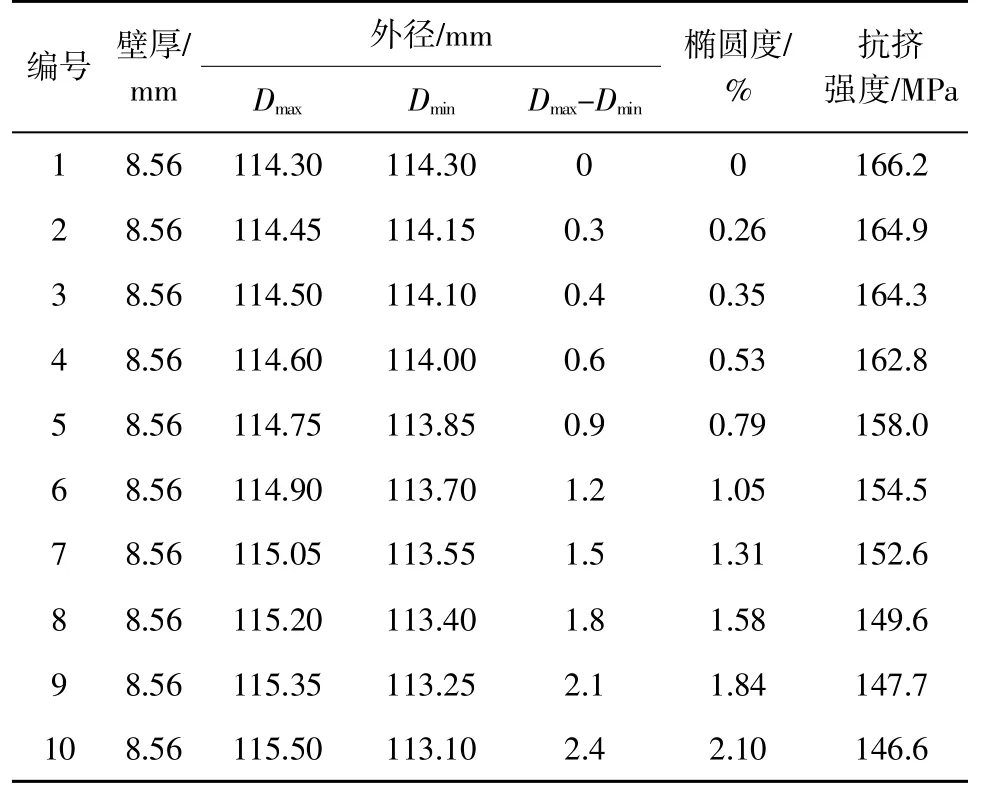
表5 140V 样管椭圆度和抗挤强度有限元结果

可见，壁厚不均度和椭圆度对套管的抗挤强度均有明显影响，但影响程度又有所不同。对壁厚不均度来说，当壁厚不均度大于5%以后，套管抗挤强度随壁厚不均度增加有加速下降的趋势。对于椭圆度来说，当其值在0～0.53%，以及大于1.05%以后，抗挤强度随椭圆度增加下降速度较慢；在0.53%～1.05%时，下降速度最快。生产高抗挤套管时需要制订相应的控制标准。

6 结语

（1）利用建立的套管外压挤毁的平面应变有限元模型可以较准确地预测Φ114.3 mm×8.56 mm V140 套管的抗挤强度，利用该模型能否预测其他规格，尚需试验验证。

（2）该规格套管属塑性挤毁，挤毁失效的机理是首先在几何缺陷较大的某些区域发生塑性屈曲，然后结构发生失稳而失效。

（3）套管壁厚不均度、椭圆度对套管抗挤毁能力有显著影响，当壁厚不均度大于5%以后，套管抗挤强度随壁厚不均度增加有加速下降的趋势，椭圆度0.5%～1.5%时，套管抗挤强度下降速度最快。