在一道有“问题”的高中数学试题中追根源、释全景

⦿ 山东省桓台第一中学 苏同安

在一些名校或地区的2021届高三数学试卷中出现了一道有“问题”的试题,不仅答案错误,而且所给的选项中也没有正确答案.

然而,试题题干本身不仅没有问题,而且还与“初中”的一类典型问题密切相关、本质相同,是值得探究和推广的.以下针对此题,运用“一题释全景”的方法,全面分析问题出现的原因,并围绕此问题进行追根求源、拓展推广,提炼出其本质内涵,生成从“二维”到“三维”相关知识方法的“全景图”.

1 试题及分析

试题如图1,在棱长为2的正方体ABCD-A1B1C1D1中,点P是该正方体棱上一点,若满足|PB|+|PC1|=m(m>0)的点P的个数为4,则m的取值范围是( ).

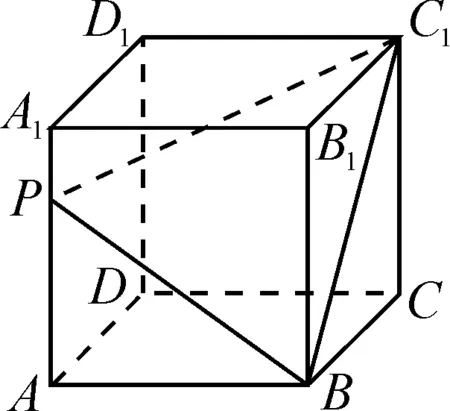
图1

命题者给出的参考答案为B,其理由是:

由椭圆(如图2)的性质,知:

图2

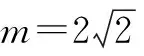
当m=4时,点P的个数为2.

实际上,点P从点A到点A1,m的值并不是单调递增,是先“递减”再“递增”——这里涉及到一个大家早已熟知且非常典型的初中的最短路径问题,把此问题进行推广(二维到三维),便能诠释当前问题的“本质内涵”,并自然生成相关知识方法的“全景图”.

2 问题探源

首先追根求源,给出初中的最短路径问题.

求源问题:在平面内,一条直线l和该直线外的两点A与B,P是直线l上一点,求PA+PB的最小值,并确定点P的位置.

解决此问题分两种情况:

一是点A与点B在直线l的异侧(如图3).只要连接AB,其与直线l的交点便是所求的点P,此时PA+PB的最小值为AB的长度;

图3

二是点A与B在直线l的同侧(如图4).作出A关于直线l的对称点A′,连接A′B,其与直线l的交点便是所求的点P,此时PA+PB的最小值为A′B的长度.

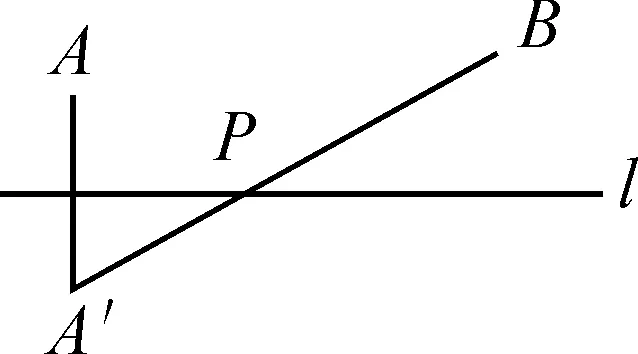
图4

3 问题推广

在空间中,一条直线l和该直线外的两点A与B,点P是直线l上一点,求PA+PB的最小值,并确定点P的位置.

解决此问题,分为如下两种情形.

(1)当两点AB与直线l共面时,属于上面的求源问题.

(2)当直线AB与直线l异面时,就是本文所分析的试题中易出问题的情形:点P在平面ADD1A1内的棱上(其中的四条棱所在直线均与直线BC1异面).

情形(2)通过图形变换可转化成为情形(1),并得到“统一性的结论”.

如图5,设点B与直线l所确定的平面为α.

图5

将点A与直线l所确定的平面以l为轴“旋转”(或折叠)到与平面α“重合”,点A的对应点为A′(让点A′与点B在l异侧).

连接A′B,则A′P=AP(也可看作是以AP为母线,l为轴旋转形成圆锥侧面的两条母线).

所以,PA+PB=PA′+PB≥A′B,当且仅当A′,P,B三点共线时,等号成立.

这样已转化为情形(1)(A′B与直线l共面),由此可总结出具有“共性”的一般结论.

一般结论:点P将直线l分为两条射线,分别与AP,BP所成角为θ和φ(如图5),当且仅当θ=φ时,PA+PB取最小值.(共面或异面的共性特征.)

此结论不仅诠释了各种情形的本质联系和共性特征,也可进一步思悟联想光线反射中的“入射角”与“反射角”相等的自然本质.

4 方法总结

根据上面的分析可知,PA+PB最小值的求法及相应点P的确定,主要有如下三种方法.

(1)图形变换法:利用相关图形的折叠或旋转,把“异面”转化为“共面”.

(2)等角计算法:利用θ=φ,确定点P的位置.(比如利用tanθ=tanφ进行计算.)

(3)设参求解法:围绕点P,设出恰当参数x,表示出PA+PB=f(x),然后求f(x)的最值.

5 回到原题

此时再回看原题,不但一清二楚,而且还能悟出此题的本质.

下面用上述三种方法简略解析本试题.重点分析当点P在棱A1A上时的情况.

方法一:如图6,将正方形ABB1A1以AA1为轴旋转到与矩形ACC1A1共面,点B的对应点为B′.

图6

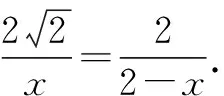
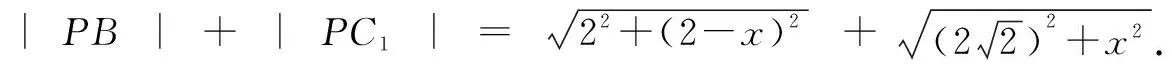
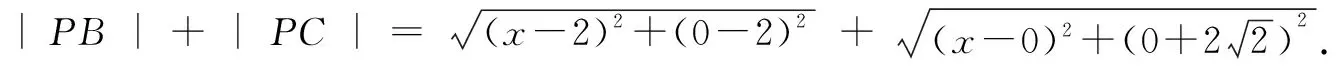
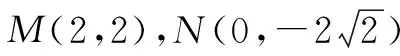
6 原题拓展

有了以上的全景分析和方法总结,自然会产生更全面深入的思考,再将原题进行拓展.

(1)正方体棱长一般化

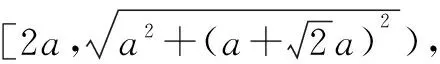
(2)正方体变为长方体

进而想到的是,把正方体变为长方体.

把试题中的正方体改为长方体,并设AB=a,BC=b,AA1=c.

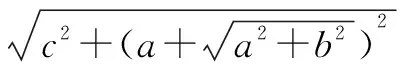
讨论b+c与其最小者的大小即可:

这样,在更为一般的情境下,更能体会到此问题的本质和价值,也会激发进一步的探究兴趣(比如围绕点P的个数进行拓展),这也是本文更广泛的意义.

以上,通过对“问题”试题进行的探究分析、追根求源、拓展推广所形成的“全景图”以及追根求源、纵横拓展的研学方法,充分体现出“一题释全景”思想理念的价值,为学习数学知识方法的“本真”带来一些启迪.