多工况下侧偏角自适应联级滑模观测
王云超,周书荣,杨雯颖
(集美大学 海洋装备与机械工程学院,福建厦门 361021)
车辆稳定性控制是车辆底盘动力学控制的核心技术,也是车辆在复杂工况下制动、驱动、转向稳定性控制的关键技术。车辆轮胎侧偏角是用来表征车辆侧向状态稳定性的重要变量[1]。在早期研究中,轮胎侧偏角通常是由试验性的模型公式推导出来[2]。随着传感器技术的不断发展,部分研究者通过直接或间接方式测量轮胎侧偏角,但是所需的成本昂贵、实现起来比较复杂,很难普及推广应用。此外,汽车复合工况一般伴随整车载荷向前后或外侧车轮转移,导致单个轮胎的侧偏特性工作区域发生转移,弱化了车轴侧偏特性,从而改变了整车的转向特性[3]。所以准确观测汽车复合工况下的轮胎侧偏角是一个难题。
目前,基于整车动力学模型的车辆轮胎侧偏角观测方法在实际动力学稳定性控制中广泛采用,具体包括神经网络观测法[4]、Kalman 滤波方法[5]、综合方法[6]等。这些方法主要对质心侧偏角进行观测,而对轮胎侧偏角观测精度不高,特别是复合工况下,观测精度和实时性取决于观测模型的复杂程度。荷兰TNO 汽车研究所对此进行了研究,通过设计卡尔曼滤波器对侧偏角进行观测,获得了比较满意的结果[3]。张小龙等根据汽车稳定性控制系统通过配置传感器信息建立神经网络模型来观测车轮轮胎侧偏角[7],将车辆侧偏角看作横摆角速度和侧向加速度时间序列的映射,而其所需权重值如需移植到其他车型时则要重新测试以获取网络学习样本[8-10]。李伟等提出了一种基于径向基神经网络的汽车侧偏角估计方法[4]。李亮等为了提高车辆轮胎侧偏角观测精度利用自适应滑模观测算法有效地减少了侧偏角的误差、同时适用性也比较广[11-15]。
上述研究方法中Kalman 滤波方法需强烈依赖于路面附着力,且需假设路面输入噪声为白噪声;神经网络模型很难对映射关系进行机理性解释,而且映射关系对试验数据具有很强的依赖性,不具有普遍性;神经网络模型在计算车辆纵向速度权重值时较为复杂,应用性不高;当滑模控制切换函数为饱和函数,并不能很好适用于连续求导的环境中,容易造成观测误差的累积。因此本文为了提高轮胎侧偏角的观测精度以及适用性,针对车辆多种工况,提出一种新型的基于自适应双曲正切滑模观测器理论的联级观测算法,并选取了双移线和紧急避障两种典型工况进行了观测验证,试验表明该方法成本较低,精度满足应用需求,为不同工况下轮胎侧偏角观测模型研究提供理论支持。
1 车辆动力学模型
1.1 车辆整车动力学模型
汽车模型简化成二自由度模型如图1 所示。

图1 二自由度汽车模型Fig.1 The Two-degree-of-freedom vehicle model
根据牛顿第二定律,忽略风阻,车辆垂直方向以及车辆俯仰和侧倾运动,车辆运动方程为:
式中:I为车辆绕z轴转动惯量;γ为车辆横摆角速度;Fx,Fy为轮胎纵向力和侧向力;vx,vy为车辆纵向和侧向速度;a,b分别为前轴、后轴到车辆质心间的距离;β为质心侧偏角;α 为侧偏角;δ为车辆轮胎转角。
当轮胎侧偏角较小时,轮胎的侧偏角可以近似为:
2 观测器设计
2.1 滑模观测器设计
滑模控制是自动控制系统的一种设计方法,具有对系统参数不确定性和外部扰动较强的鲁棒性,故滑模一阶系统设计观测器可表示为:
式中:x为 系统的状态;u为 系统的输入;d为未知并且有界的输入;y为测量输出;ψ为其它干扰项;B、P分别为实常数。
以滑模面为系统误差 ε=x-,设计李亚普诺夫函数为
式中:L为反馈增益;ρ为滑模增益。
由式(3)和式(5)可得系统误差导数为
2.2 侧偏角自适应联级滑模设计
2.2.1 双曲正切滑模设计
使用符号函数或饱和函数作为滑模控制的切换函数时,由于其属于不连续函数,不适合对切换函数求导的场合,而车辆行驶时多为复合工况,这将会加剧滑模的抖振,为此,本文采用双曲正切函数tanh(ε)代替符号函数sign(ε),其中,tanh(ε)=,且ε>0。
因此,前轮侧偏角观测器的形式可表述为
式中:ρf为前轮侧偏角滑模观测器的滑模增益;L1为前轮侧偏角滑模观测器的反馈增益。
同理,后轮侧偏角自适应双曲正切滑模观测器为
式中:ρr为后轮侧偏角滑模观测器的滑模增益;L2为后轮侧偏角滑模观测器的反馈增益。
2.2.2 轮胎侧向力滑模观测器设计
根据式(1)可求得侧向力,并由式(7)可得前轮轮胎侧向力滑模观测器为
式中:ρy1为车轮的纵向轮胎力滑模观测器的滑模增益;Ly1为车轮的纵向轮胎力滑模观测器的反馈增益。同理,后轮侧向轮胎力滑模观测器为
2.2.3 自适应联级滑模观测器设计
为提高系统鲁棒性,引入误差自适应鲁棒控制[16],则根据式(3)和式(8)可得
由式(10)和式(11)可得轮胎侧向力滑膜观测值与离心力的自适应观测误差为
联立式(8)、式(12)和式(13),可得前轮轮胎侧偏角观测值为
同理,后轮轮胎侧偏角观测值为
3 仿真对比分析
为了验证本文提出观测算法的有效性,基于CarSim 与Simulink 软件建立车辆联合仿真型,真实值为CarSim 车辆仿真模型侧偏角的输出值。车辆基本参数如表1 所示。

表1 车辆基本参数Tab.1 Basic vehicle parameters
3.1 双移线工况
为验证自适应联级滑模观测算法的准确性,首先针对双移线工况,开展了15 m/s、30 m/s 速度的道路仿真试验,道路附着系数为0.5,仿真结果如图2~图5 所示。
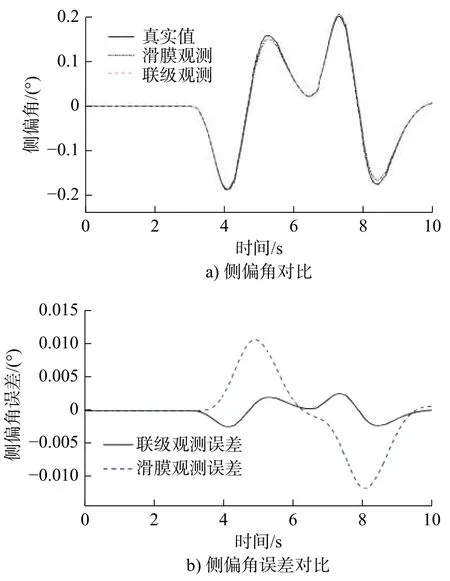
图2 前轮侧偏角与误差对比图Fig.2 Comparison of front wheel slip angle and error
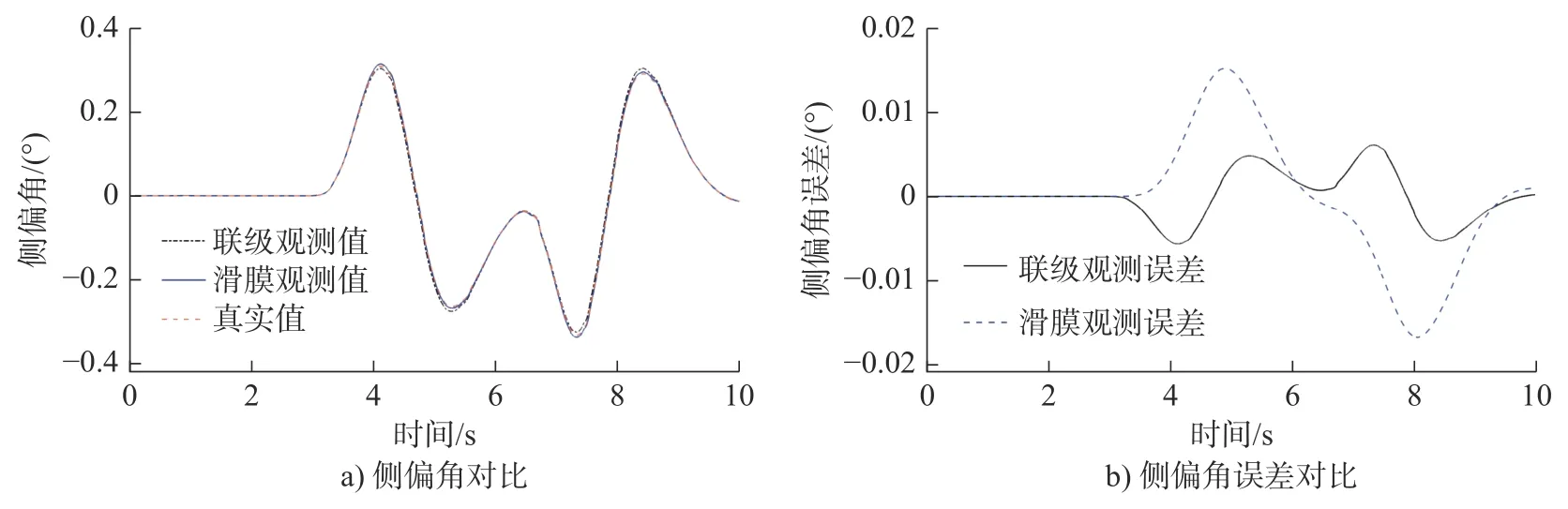
图3 后轮侧偏角与误差对比图Fig.3 Comparison of rear wheel slip angle and error
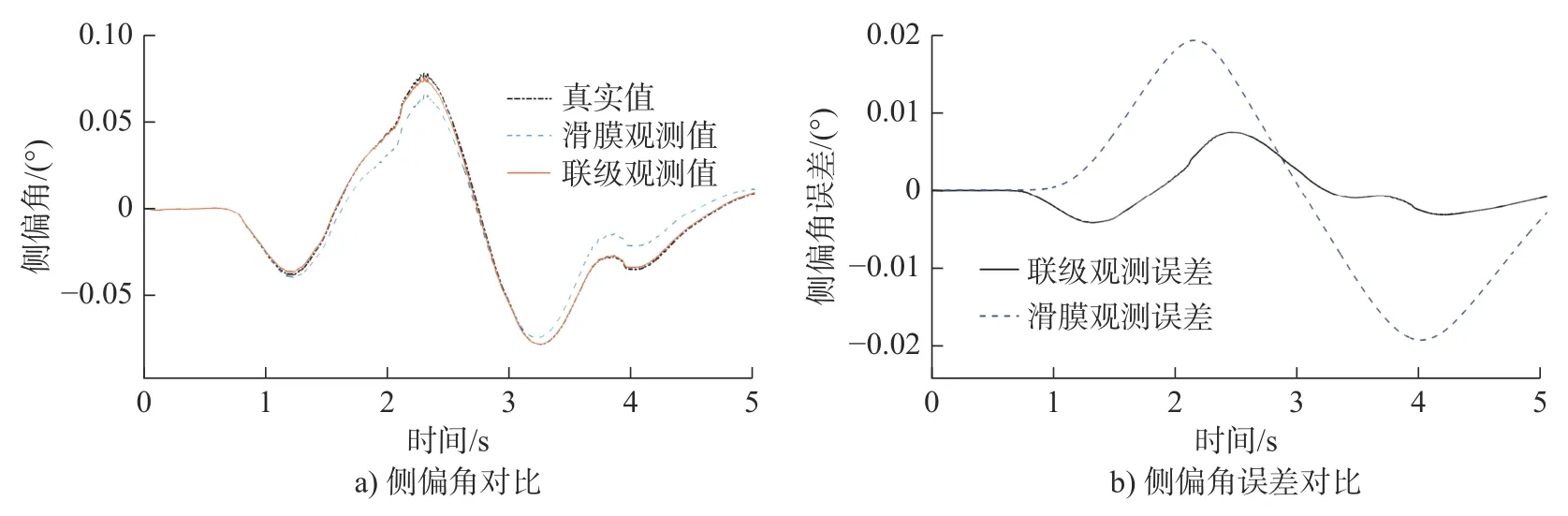
图4 前轮侧偏角与误差对比图Fig.4 Comparison of front wheel slip angle and error
从图2~图5 可知:速度越大,导致滑模观测的侧偏角效果变差。相较于滑模观测算法,自适应联级滑模观测算法的精度更高、尖峰波动较缓且能够很快趋于稳定,有效地提高观测系统的精度。
双移线工况误差占比如表2 所示,结果表明:当速度提高至30 m/s 后,误差也会随着增大,但自适应联级滑模观测算法的鲁棒性强,能有效的控制误差的增幅,具有更好的优越性。
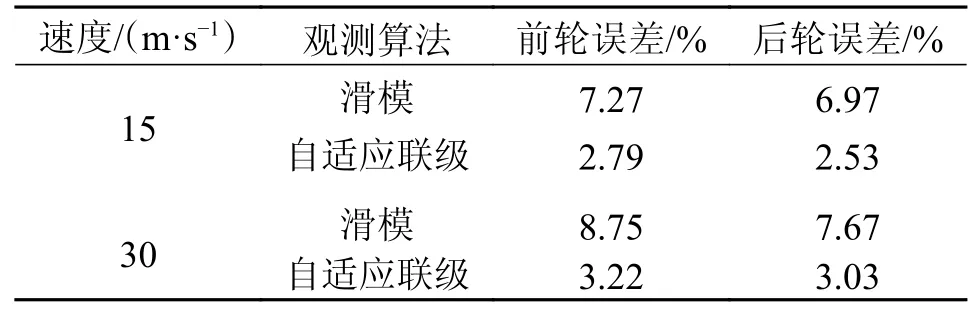
表2 双移线工况误差占比Tab.2 Error percentage for the double-shift-line working condition
3.2 紧急避障工况
为进一步验证算法的鲁棒性,进行了紧急避障道路仿真试验,紧急避障时车辆的行驶速度如图6所示。
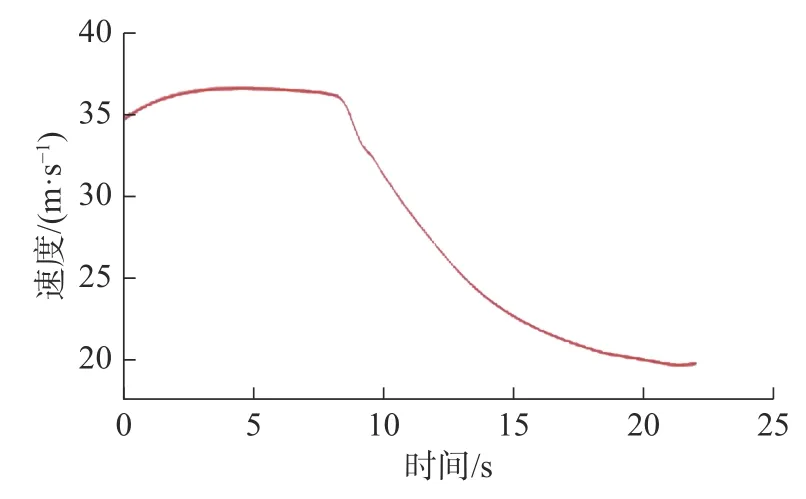
图6 车辆行驶速度Fig.6 Vehicle speed
仿真的观测效果与误差对比见图7 和图8。从图7 和8 可知:相对滑模观测算法,自适应联级滑模观测算法的避障侧偏角误差波动幅度相对较大,其主要原因是侧向力观测误差导致,但是其鲁棒性很好,而滑模观测算法出现误差累积的现象。

图7 前轮侧偏角与误差对比图Fig.7 Comparison of front wheel slip angle and error

图8 后轮侧偏角与误差对比图Fig.8 Comparison of rear wheel slip angle and error
紧急避障误差占比如表3 所示,结果表明:在紧急避障下,自适应联级滑模观测算法能将误差有效控制在5%以内,相对滑膜观测算法,观测精度提高了61.4%,观测精度和鲁棒性明显提高。
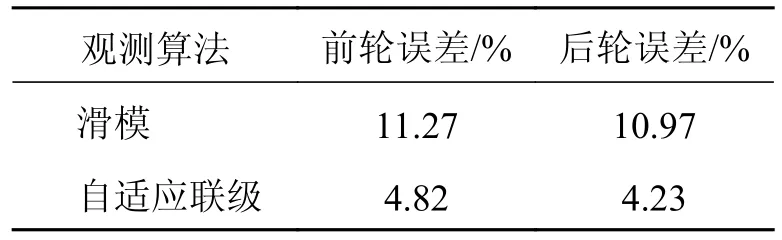
表3 紧急避障误差占比Tab.3 Error percentage for emergency obstacle avoidance
4 结论
1)提出了一种侧偏角自适应滑模联级观测算法,基于CarSim 与Simulink 软件建立了车辆联合仿真。
2)通过增加侧向力联级观测以及误差自适应鲁棒性控制,能有效地减小误差累积,增强算法的鲁棒性、进而提高算法的观测精度,更能满足实时性的要求。
3)通过多种不同工况验证了当在道路条件较为恶劣且转向变化剧烈的工况下,自适应联级滑模观测算法的抗干扰能力与适应能力优于滑模观测算法。体现算法的有效性和可行性,为实车的轮胎侧偏角研究提供了理论基础。

