Underlying mechanisms of variation in yield asymmetry and strain hardening behavior of extruded pure Mg with Gd addition

Gyo Myeong Lee,Sung Hyuk Park

School of Materials Science and Engineering,Kyungpook National University,Daegu 41566,Republic of Korea

Abstract Effects of Gd addition on the strain hardening behavior and yield asymmetry of pure Mg are investigated by subjecting extruded pure Mg,Mg–5Gd,and Mg–15Gd (all in wt%) to tension and compression tests along the extrusion direction (ED).As the amount of Gd added to pure Mg increases,the basal texture tilts toward the ED and the distribution of c-axes of grains becomes randomized.Under tension,the strain hardening rates of all the materials decrease until fracture.However,under compression,the strain hardening rate increases in the early stage of deformation in pure Mg and Mg–5Gd,whereas it continuously decreases in Mg–15Gd.Pure Mg exhibits considerably high tension-compression yield asymmetry,with a compressive yield strength (CYS) to tensile yield strength (TYS) ratio of 0.4.In contrast,Mg–5Gd exhibits excellent yield symmetry with CYS/TYS of 0.9 and Mg–15Gd exhibits reversed yield asymmetry with CYS/TYS of 1.2.Underlying mechanisms of these drastically different Gd-addition-induced deformation behaviors of the materials are discussed in terms of the crystallographic distribution of grains and the relative activation stresses of basal slip,prismatic slip,pyramidal slip,and {10–12}twinning under tension and compression.

Keywords: Pure Mg;Gd addition;Texture;Yield asymmetry;Activation stress.

1.Introduction

Demands for the application of lightweight materials in the automotive industry have increased owing to the recent tightening of international environmental regulations aimed at reducing the carbon dioxide emissions of vehicles.In this regard,Mg alloys have recently attracted significant attention because of their lower density and higher specific strength than steels and Al alloys.Long products with various crosssectional shapes can be easily fabricated via the extrusion process,and the mechanical properties of extruded products made of Mg alloys are enhanced than those of their cast counterparts [1,2].However,there is generally a large difference between the compressive yield strength (CYS) and the tensile yield strength (TYS) of extruded Mg alloys,and these alloys have low forming performance at room temperature (RT);both these characteristics are attributed mainly to their strong basal texture [3] and limit their widespread industrial application.In recent decades,numerous studies have attempted to overcome these shortcomings of extruded Mg alloys by improving their formability and reducing their yield asymmetry.

The addition of rare-earth (RE) elements to pure Mg can induce the generation of a weak and tilted basal texture (i.e.,RE texture) in the extruded material rather than the typical basal texture of extruded pure Mg,in which most basal planes are aligned parallel to the extrusion direction (ED) [4–7].The RE texture facilitates the activation of basal slip under tensile deformation along the ED at RT;consequently,extruded Mg–RE alloys with an RE texture exhibit better RT ductility and formability than extruded RE-free Mg alloys with a typical basal texture [8–10].Among the various available RE elements,Gd has an extremely high solubility limit in Mg(23.3 wt%) [11],which enables design of Gd-containing Mg alloys with a wide composition range and induction of significant solid-solution strengthening and precipitation strengthening effects through heat treatment [12].In addition,Gd addition to pure Mg and Mg alloys reduces the tension–compression yield asymmetry(i.e.,the CYS/TYS ratio)of the final wrought materials.For example,Kula et al.[8] reported that when 2.9 wt% Gd is added to pure Mg,the CYS/TYS ratio of the rolled material increases significantly,from 0.21 to 0.83,owing to the balanced activation of dislocation slip and deformation twinning under tension and compression.Chi et al.[13] demonstrated that an extruded Mg–8.4Gd–2.3Y–0.2Zr (wt%) alloy exhibits excellent yield symmetry because of the initial yielding via the same deformation modes (basal slip and prismatic slip) under both tension and compression.Furthermore,Gd addition can improve the strength of wrought Mg materials through the twin boundary pinning effect [14],particle strengthening effect of fine Mg–Gd precipitates [15],and grain-refining effect induced by the grain-boundary segregation of Gd [15,16].

The effects of Gd addition on the deformation behavior of Mg alloys have been analyzed using various methods,such as the viscoplastic self-consistent model [17,18],insituelectron backscatter diffraction (EBSD) analysis [10,19],lattice strain measurement [13,20],slip trace analysis [19,21],and modified lattice rotation analysis [22].However,no in-depth studies have yet been conducted to investigate the deformation behavior of extruded Mg–Gd alloys via the quantitative analysis of the critical resolved shear stresses (CRSSs) of active deformation modes under tension and compression.This analysis approach is expected to broaden our understanding of the deformation mechanisms and yield asymmetry behaviors of extruded Mg–Gd alloys and wrought Mg alloys with a tilted basal texture [23–27].Moreover,a previous study demonstrated that as the amount of Gd added to pure Mg increases from 1 to 15 wt%,the orientation with a maximum texture intensity in ED inverse pole figure (IPF) of the extruded material gradually varies from the <2–1–11>to <0001>direction [15].That is,an extruded Mg–1Gd alloy has a <2–1–11>texture,which is a typical RE texture,whereas an extruded Mg–15Gd alloy has a <0001>texture,which is an extraordinary RE texture with basal poles parallel to the ED [15].Extensive studies have been conducted on the tensile and compressive deformation behaviors of wrought Mg alloys with a typical <2–1–11>RE texture,such as the extruded Mg–1Gd alloy.In contrast,few studies have been conducted on the deformation behavior and active slip/twinning systems of wrought Mg alloys with unusual RE textures,such as the extruded Mg–15Gd alloy.Therefore,in this study,variations in the mechanical properties—especially the yield asymmetry and strain hardening rate—of extruded pure Mg with large amounts of Gd addition are investigated through tension and compression tests of extruded pure Mg,Mg–5Gd,and Mg–15Gd (all in wt%) at RT.Additionally,the underlying mechanisms of these variations are analyzed by considering the relative activation stresses of basal slip,prismatic slip,pyramidal slip,and {10–12} twinning under tension and compression.

2.Experimental procedure

Billets of pure Mg,Mg–5Gd,and Mg–15Gd (all in wt%)were used in this study.Pure Mg ingots were melted with or without Gd granules (purity: 99.9%) in an electric resistance furnace and subsequently cast into a cylindrical steel mold preheated to 200 °C.Considering the solidus temperatures of Mg–5Gd and Mg–15Gd (approximately 610 °C and 560 °C,respectively [11]),cast billets of pure Mg,Mg–5Gd,and Mg–15Gd were homogenized at 500 °C for 24 h and then water-quenched.During homogenization,a mixture of SF6and CO2gases was injected into an electric furnace to prevent excessive oxidation and local melting at the surface.Cylindrical samples (diameter: 80 mm,height: 200 mm) were cut from the homogenized billets for the hot extrusion process.The cylindrical samples were then preheated with an extrusion die in an electric furnace at the target extrusion temperature (450 °C).Indirect extrusion was performed at a temperature of 450 °C,extrusion ratio of 25,and ram speed of 1 mm/s using a horizontal type-hydraulic extrusion machine.The fabricated extruded bars (diameter: 16 mm) were cut to obtain specimens for tension and compression tests.Dogbone-shaped specimens (gage length: 25 mm,gage diameter:6 mm)were machined for tension testing,and cylindrical specimens(height:9 mm,diameter:6 mm)were machined for compression testing;the longitudinal direction of all the specimens corresponded to the ED.All the tension and compression tests were performed using a Shimadzu AGS-100kNX universal testing machine at RT (23 °C) with a strain rate of 10-3s-1.

To analyze the microstructural and textural characteristics of the extruded materials and the fractured tensile and compressive specimens,the cross-sectional planes parallel to the ED were polished first with progressively finer grades of emery paper (#120–#2000 grit),then with 3 and 1 μm diamond pastes,and finally with colloidal silica.Sample characterization was performed using optical microscopy (OM),field-emission scanning electron microscopy (FE-SEM),and EBSD anlaysis.EBSD measurements were performed using an EBSD detector (Symmetry S2,Oxford Instruments)mounted on a field-emission scanning electron microscope with an accelerating voltage of 20 kV and a working distance of 17.0 mm.EBSD scanning was performed using a different step size for each extruded material and fractured specimen;specifically,the step size used for a given sample was smaller than 1/20th of its average grain size.EBSD analysis was performed using AZtecCrystal 2.0 software (Oxford Instruments),and only those data with a mean angular deviation smaller than 1.0 were used to ensure the accuracy of the analysis results.

Both the deviation angle between thec-axes of grains and the loading axis (hereafter referred to as angleθ) and the deviation angle between thea-axes of grains and the loading axis (hereafter referred to as angleα) were considered in the calculation of the activation stresses of the deformation modes (basal slip,prismatic slip,pyramidal slip,and {10–12}twinning).Because thea-axes of grains did not have specific crystallographic orientations in all the extruded materials,the average Schmid factor (SF) values for slip systems were obtained by averaging their SF values atα=0° and 30°.The average SF values for {10–12} twinning were obtained by averaging the maximum SF values of the six equivalent twin variants atα=0° and 30° in individual grains.

3.Results

3.1. Microstructural characteristics of extruded materials

Fig.1 shows the microstructures of the homogenized billets and extruded materials.The average grain sizes of the pure Mg,Mg–5Gd,and Mg–15Gd billets are 469,608,and 4412 μm,respectively,which indicates that the Gd addition leads to the grain coarsening of the cast pure Mg.These grain sizes of the billets significantly decrease to 116.8,48.7,and 47.3 μm,respectively,after extrusion.The grain size of a billet before extrusion can affect the microstructure of the extruded material because grain boundaries of the billet are the main nucleation site for recrystallized grains during extrusion.Barnett et al.[28] reported that as the grain size of an AZ31 billet decreases,the area fraction of recrystallized grains of the extruded material increases owing to the increased number of nucleation sites for dynamic recrystallization (DRX).However,the size of recrystallized grains of the extruded material does not change with the billet grain size [28].Park et al.[29] investigated the effect of billet grain size on the microstructure and mechanical properties of an extruded AZ91 material.They also demonstrated that the size and area fraction of unrecrystallized grains decrease with decreasing billet grain size,but the size of recrystallized grains remains the same regardless of the billet grain size[29].When an extruded Mg material has a partially recrystallized grain structure consisting of unrecrystallized grains and recrystallized grains,the billet grain size can affect the average grain size of the extruded material due to the variations in the size and fraction of unrecrystallized grains.However,in the present study,because of the high extrusion temperature(450 °C) and high extrusion ratio (25),the heat and strain energies applied to the materials during extrusion are sufficient to cause complete DRX;consequently,all the extruded materials have a completely recrystallized grain structure devoid of unrecrystallized grains.Therefore,the effect of different grain sizes of the pure Mg,Mg–5Gd,and Mg–15Gd billets on the average grain size of the extruded materials is negligible.

Fig.1.(a-c) Optical images of homogenized billets and (d-f) optical and (g-i) SEM images of extruded materials: (a,d,g) pure Mg,(b,e,h) Mg–5Gd,and(c,f,i) Mg–15Gd.davg,fppt,and dppt denote the average grain size,area fraction of Mg5Gd particles,and average size of Mg5Gd particles,respectively.

As the Gd content increases from 0 to 5 wt%,the average grain size of the extruded material decreases significantly from 116.8 to 48.7 μm.It has been reported that Gd solute atoms and Mg–Gd precipitates inhibit grain-boundary movement during the extrusion process.For example,Hadorn et al.[16] demonstrated that the addition of even a small amount of Gd (0.06 at%) can refine the grain size of extruded pure Mg through the grain-boundary segregation of Gd solute atoms during extrusion.As can be seen in Fig.1h,the extruded Mg–5Gd material,hereafter denoted as Mg–5Gd,contains a small amount of fine Mg5Gd precipitates (area fraction:0.2%);therefore,most Gd atoms dissolve in the Mg matrix to form a solid solution.The refined grains in Mg–5Gd are mainly attributed to the suppressed migration of grain boundaries by the solute drag effect and to the grain-boundary segregation of Gd solute atoms.However,despite the considerably higher Gd content,the average grain size of the extruded Mg–15Gd material,hereafter denoted as Mg–15Gd,is comparable (47.3 μm) to that of Mg–5Gd (48.7 μm);this result is contrary to previously reported results for extruded Mg–Gd materials [15].Kim et al.[15] reported that the average grain size of an extruded Mg–15Gd material (4.3 μm) is significantly smaller than that of an extruded Mg–5Gd material(16.7 μm),because during extrusion,fine Mg5Gd precipitates uniformly distributed in the former inhibit grain coarsening through their grain-boundary pinning effect.In their study[15],extrusion is performed at a relatively low temperature of 350 °C;therefore,a large amount of Mg5Gd precipitates are formed throughout the extruded Mg–15Gd material because the added amount of Gd (15 wt%) exceeds the Gd solubility limit at the temperature of the deformation zone during extrusion (9.7 wt%).However,in the present study,as the Gd content significantly increases from 5 to 15 wt%,the area fraction of Mg5Gd precipitates in the extruded material slightly increases from 0.2% to 0.8%.Moreover,the average size of Mg5Gd precipitates increases from 0.4 μm for Mg–5Gd to 0.9 μm for Mg–15Gd;consequently,the difference in the number density of Mg5Gd precipitates in Mg–5Gd and Mg–15Gd is small.The Gd solubility limit at the extrusion temperature adopted in the present study (450 °C) is as high as 15.7 wt% [11],and therefore,only a small amount of Mg5Gd precipitates is locally formed along the ED in Mg–15Gd.Consequently,the precipitate-induced grain refinement effect is insignificant in both Mg–5Gd and Mg–15Gd.It is notable that although the concentration of Gd solute atoms is considerably higher in Mg–15Gd than in Mg–5Gd,the two extruded materials have almost the same average grain size.This result suggests that grain refinement through the grain-boundary segregation and solute drag effect of Gd solute atoms occurs to the maximum possible extent in Mg–5Gd.

3.2. Tensile and compressive properties of extruded materials

Fig.2a and b shows the true tensile and compressive stressstrain curves of the extruded materials,respectively,and Table 1 lists their corresponding properties.The addition of 5 wt% Gd significantly increases both the tensile elongation(TE) and compressive elongation (CE) of pure Mg from 5.8%to 22.3% and from 15.5% to 33.2%,respectively.Previous studies have also reported that the addition of less than 6 wt% Gd to pure Mg increases the TE of the extruded material through grain refinement and promotes the activation of basal and nonbasal slips [10,22].However,in the present study,as the amount of Gd added to pure Mg increases from 5 to 15 wt%,the TE and CE of the extruded material decrease from 22.3% to 7.5% and from 33.2% to 16.7%,respectively.Fig.3 shows the optical microstructures of the longitudinal cross sections of the fractured tensile specimens.In the fractured specimens of all the extruded materials,cracks are formed along the twins,not at the grain boundaries,precipitates,and interface between the precipitate and the matrix.In extruded Mg alloys,{10–11} contraction twinning and {10–11}–{10–12} double twinning generally occur under tension along the ED,and these contraction and double twinning cause lattice reorientations of approximately 56°and 38°,respectively.Hence,dislocation accumulation and lattice distortion are concentrated inside the contraction and double twins during further deformation;consequently,microcracks are initiated at the twins [30].Xu et al.[12] reported that the solid solution strengthening effect of Gd in Mg is consid erably stronger than that of widely used alloying elements,such as Al,Zn,and Sn.Because of the large atomic radius of Gd (0.363 nm),a considerable volumetric strain field is formed around substitutional Gd solute atoms,which hinders the movement of dislocations and increases the resolved shear stress required for plastic deformation.Accordingly,an increase in Gd content added to pure Mg results in a gradual improvement in the strength of the material;however,its ductility deteriorates at the expense of the improved strength.Although the degrees of the grain boundary hardening and precipitate hardening effects in Mg–5Gd and Mg–15Gd are similar,the solid solution hardening effect and corresponding ductility loss are higher in the latter owing to its higher Gd content.As the amount of Gd atoms dissolved in the Mg matrix increases,the activation of basal slip under tension and compression at RT is suppressed,which eventually reduces the ability to accommodate deformation via dislocation slip.As a result,{10–11} contraction twins and {10–11}–{10–12}double twins,which act as crack initiation sites,can be generated earlier during deformation in a Mg alloy with a higher Gd content.Therefore,Mg–15Gd with a higher concentration of Gd solute atoms exhibits lower tensile and compressive ductility than Mg–5Gd.

Table 1Tensile and compressive properties of extruded materials.TYS,UTS,TE,CYS,UCS,and CE denote the tensile yield strength,ultimate tensile strength,tensile elongation,compressive yield strength,ultimate compressive strength,and compressive elongation,respectively.

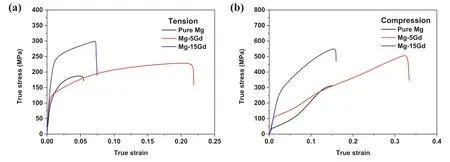
Fig.2.(a) Tensile and (b) compressive true stress–strain curves of extruded materials.

Fig.3.Optical images of fractured tensile specimens of (a) pure Mg,(b) Mg–5Gd,and (c) Mg–15Gd.

The TYS and CYS,along with the ultimate tensile strength(UTS) and ultimate compressive strength (UCS),of the extruded material gradually increase with increasing Gd content.Fig.4 shows the variations in the TYS,CYS,and yield asymmetry (=CYS/TYS) with the Gd content.The TYS and CYS of pure Mg are 112.4 and 39.5 MPa,respectively;this outstanding difference of 72.9 MPa leads to high yield asymmetry (CYS/TYS=0.4).When 5 wt% Gd is added to pure Mg,the TYS of the extruded material increases by 12.1 MPa,whereas its CYS increases by 69.4 MPa.Consequently,the difference between the TYS and the CYS decreases considerably,from 72.9 to 15.6 MPa,and Mg–5Gd exhibits low yield asymmetry(CYS/TYS=0.9).When the Gd content increases from 5 to 15 wt%,the TYS and CYS of the extruded material increase by 110.9 and 165.0 MPa,respectively.As a result,Mg–15Gd exhibits reversed yield asymmetry,with its CYS being greater than its TYS (CYS/TYS=1.2).When the amount of Gd added to pure Mg increases to 15 wt%,the increment in the CYS of the extruded material (from 39.5 to 273.9 MPa) is ∼1.9 times that in its TYS (from 112.4 to 235.4 MPa),which,in turn,results in a drastic increase in the CYS/TYS ratio,from 0.4 to 1.2.

Fig.4.(a) Variations in tensile yield strength (TYS) and compressive yield strength (CYS) of extruded materials with Gd content and (b) tension–compression yield asymmetry data (i.e.,CYS/TYS ratios) of extruded materials.

3.3. Textural characteristics of extruded materials

The IPF and kernel average misorientation(KAM)maps of the extruded materials are shown in Fig.5.The KAM value is directly related to the density of geometrically necessary dislocations in a material [31].All the extruded materials have low average KAM values (0.22,0.26,and 0.27 for pure Mg,Mg–5Gd,and Mg–15Gd,respectively),which indicates that the dislocations generated by the stress imposed during extrusion are mostly annihilated through DRX and recovery processes.Unlike the colors of the KAM maps,those of the IPF maps differ among the three materials.The area fraction of red-colored grains,whosec-axis is almost parallel to the ED,increases with increasing Gd content.The (0001) and (10–10) pole figures (PFs) and the distributions of the deviation angle of thec-axis from the ED (i.e.,angleθ) of the extruded materials are shown in Fig.6.In pure Mg,the (0001)poles of the grains are mostly aligned perpendicular to the ED,with a high maximum texture intensity of 11.6 (Fig.6a),and grains withθlower than 55° are absent (Fig.6d).In addition,asθincreases from 55° to 90°,the area fraction of corresponding grains gradually increases,which results in a high average deviation angle of 78.7°.In Mg–5Gd,the(0001)poles are tilted slightly toward the ED compared to those of pure Mg,and their maximum texture intensity (5.9) is significantly lower than that of pure Mg (11.6) (Fig.6b).The area fraction of grains withθhigher than 70° in Mg–5Gd(45.6%) is considerably lower than that in pure Mg (79.0%),whereas grains withθranging from 30° to 55° are present in Mg–5Gd (with an area fraction of 16.8%),unlike in pure Mg.Consequently,thec-axes of the grains are more widely distributed in Mg–5Gd than in pure Mg,and Mg–5Gd has a lower average deviation angle (68.6°) than pure Mg (78.7°).In Mg–15Gd,the maximum-intensity direction of the (0001)poles is almost parallel to the ED (Fig.6c);this ED-oriented(0001) PF is consistent with the previously reported result for a Mg–15Gd material extruded at 350°C [15].Unlike the area fractions of grains in pure Mg and Mg–5Gd,which increase with increasingθ,the area fraction of grains in Mg–15Gd is distributed relatively evenly over the entire range ofθ(Fig.6d).As a result,in Mg–15Gd,the area fraction of grains withθof 0°–45° (47.1%) is almost the same as that of grains withθof 45°–90° (52.9%),and the average deviation angle of Mg–15Gd (49.2°) is considerably lower than those of pure Mg and Mg–5Gd (78.7° and 68.6°,respectively).Furthermore,as the Gd content increases from 0 to 5 to 15 wt%,the maximum texture intensity of the (10–10) PF decreases from 4.6 to 3.2 to 2.6.These drastic variations in the basal texture of the extruded material with Gd addition are consistent with previous results on the texture of wrought Mg–Gd materials[15,22,32,33].Many studies have been conducted on the mechanisms underlying the weakening and tilting of the basal texture of wrought Mg alloys induced by Gd addition.The formation of a weak and tilted texture during hot metal forming processes in Gd-containing Mg alloys is attributed to the combined effects of several phenomena,including the enhanced activation of nonbasal slips [34],promoted formation of shear bands and occurrence of DRX in them [34,35],changes in the stacking fault energy [36],and variation in grain-boundary characteristics with the segregation of RE solute atoms [16].Kim et al.[15] analyzed textural changes in extruded Mg–Gd binary alloys with the Gd content in a wide alloying range of 1–15 wt% Gd.They found that the texturetilting effect is gradually enhanced with increasing Gd content and the addition of more than 10 wt%Gd to pure Mg can lead to the development of an unusual ED//<0001>basal texture.Their results are consistent with the textures of Mg–5Gd and Mg–15Gd observed in the present study.

Fig.5.IPF maps and kernel average misorientation (KAM) maps of (a) pure Mg,(b) Mg–5Gd,and (c) Mg–15Gd.KAMavg denotes the average KAM value.

Fig.6.EBSD results showing crystallographic orientations of extruded materials: (0001) and (10–10) pole figures of (a) pure Mg,(b) Mg–5Gd,and (c)Mg–15Gd,and (d) area fractions of grains as a function of deviation angle of c-axis of grains from ED.

4.Discussion

4.1. Variation in strain hardening behavior with Gd addition

Fig.7a and b shows the strain hardening rate curves of the extruded materials under tension and compression,respectively.It is known that during the deformation of Mg alloys,an increase in the strain hardening rate after yielding indicates the occurrence of {10–12}-twinning-induced hardening via twin boundary hardening [37],the Basinski effect[38],and texture hardening [39] whereas a gradual decrease in the strain hardening rate indicates the prevalence of dislocation slip activation [40].During tensile deformation,the strain hardening rates of all the extruded materials decrease after yielding;this result implies that in all the materials,dislocation slip is the main deformation mode under tension(Fig.7a).During compressive deformation,the strain hardening rate of pure Mg rapidly decreases until the yield point and subsequently increases to 3000 MPa at a strain of ∼0.1(Fig.7b).The compressive strain hardening rate of Mg–5Gd also increases after yielding,but the amount of increase in this strain hardening rate is smaller (i.e.,up to 1900 MPa)than that of pure Mg and the strain value up to which the strain hardening rate increases is also smaller (up to a strain of 0.09) than that in the case of pure Mg.In contrast,the compressive strain hardening rate of Mg–15Gd gradually decreases until fracture,without any intervening increase.These variations in the strain hardening rates indicate that in pure Mg and Mg–5Gd,dislocation slip predominantly occurs under tension and {10–12} twinning predominantly occurs in the early stage of deformation (up to a strain of ∼0.1) under compression,whereas in Mg–15Gd,dislocation slip is the dominant deformation mode under both tension and compression.

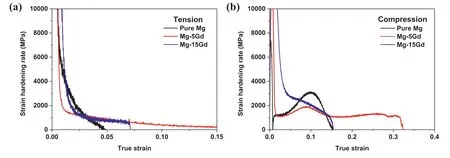
Fig.7.(a) Tensile and (b) compressive strain hardening rate curves of extruded materials.

The variation in the twinning behavior with the Gd content is analyzed by examining those grains in the extruded materials in which {10–12} twinning can occur (i.e.,grains with positive SF values for {10–12} twinning) under tension and compression along the ED,as shown in Fig.8a–f.The average SF values for {10–12} twinning of these twinning-possible grains are shown in Fig.8g.Pure Mg does not have any twinning-possible grains under tension;however,under compression,twinning is possible in all the grains,with an average SF value of 0.41.The high area fraction of the twinningpossible grains and their high average SF value under compression facilitate an increase in the strain hardening rate during compressive deformation,which is not observed during tensile deformation.Similarly,Mg–5Gd has a small area fraction of twinning-possible grains under tension (5.9%),whose average SF value is 0.31;consequently,slip-dominated deformation occurs under tension.Because the area fraction of the twinning-possible grains under compression is substantially large (94.1%) in Mg–5Gd,{10–12} twinning can occur throughout the material under compression.However,the average SF value of the twinning-possible grains under compression in Mg–5Gd (0.34) is lower than that in pure Mg(0.41).It has been previously reported that the SF value for{10–12} twinning under compression along the ED decreases with decreasingθ[41].The area fractions of grains withθof>70°andθof 30°–70°in Mg–5Gd are smaller and larger,respectively,than the corresponding area fractions in pure Mg(Fig.6d),because of which the averageθof Mg–5Gd is lower.Therefore,the average SF value for {10–12} twinning of Mg–5Gd is lower than that of pure Mg.Furthermore,because grains withθof 30°–70° are favorable for basal slip,basal slip can be activated under compression in Mg–5Gd.Therefore,during compressive deformation,the activation of basal slip is more pronounced and the activation of {10–12}twinning is less pronounced in Mg–5Gd than in pure Mg.Consequently,the degree of increase in the strain hardening rate under compression is smaller in Mg–5Gd than in pure Mg (Fig.7b).It has been reported that when a Mg alloy is subjected to plastic deformation,the strain range in which the strain hardening rate increases becomes narrower with decreases in the area fraction and SF value of twinning-possible grains [39,42].The area fraction and average SF value of twinning-possible grains under compression are smaller and lower,respectively,in Mg–5Gd than in pure Mg;therefore,the strain range in which the strain hardening rate increases is narrower in the former.In addition,{10–12} twinning is the major deformation mode under compression in both pure Mg and Mg–5Gd.However,because the activation of {10–12} twinning under compression is much less pronounced in Mg–5Gd than in pure Mg,the CYS of Mg–5Gd is substantially higher than that of pure Mg,and consequently,the yield asymmetry of Mg–5Gd is lower.

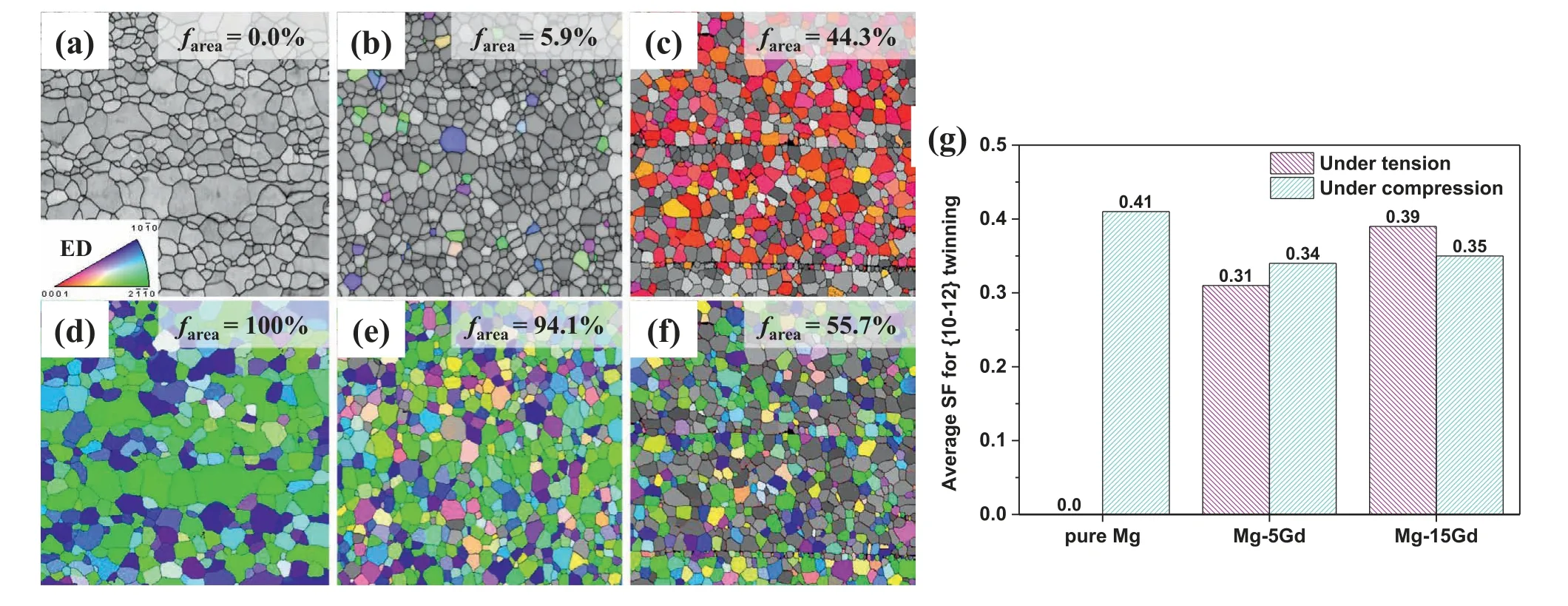
Fig.8.EBSD results showing grains in which {10–12} twinning can occur (colored grains) under (a–c) tension and (d–f) compression along ED for (a,d)pure Mg,(b,e) Mg–5Gd,and (c,f) Mg–15Gd.(g) Average Schmid factor (SF) values for {10–12} twinning of twinning-possible grains under tension and compression.farea denotes the area fraction of twinning-possible grains.

In Mg–15Gd,the area fraction and average SF value of twinning-possible grains under compression are 55.7% and 0.35,respectively.Although the average SF value of the twinning-possible grains in Mg–15Gd is comparable to that in Mg–5Gd (0.34),their area fraction in Mg–15Gd is significantly smaller than those in the other two materials (100%and 94.1% in pure Mg and Mg–5Gd,respectively).Because of the small area fraction and relatively low SF value of twinning-possible grains in Mg–15Gd,dislocation slip is the main deformation mode under compression;hence,the strain hardening rate of this material continuously decreases during compressive deformation,unlike those of the other two materials.Under tension,the area fraction and average SF value of twinning-possible grains in Mg–15Gd are 44.3% and 0.39,respectively.The difference between the area fractions of twinning-possible grains under tension and compression is extremely high in pure Mg and Mg–5Gd (100% and 88.2%,respectively);however,this difference is relatively insignificant in Mg–15Gd (11.4%).Xu et al.[20] reported that an increase in the concentration of Gd solute atoms in the Mg matrix induces the activation of prismatic slip even at low stress,which,in turn,suppresses the activation of{10–12}twinning.Their results are consistent with the suppressed{10–12}twinning and promoted nonbasal slip observed in Mg–Y and Mg–Gd alloys by Kula et al.[8].Basu and Al-Samman [43] also reported that the significant diameter difference between Gd and Mg atoms causes an increase in the activation energy for the atomic shuffling of {10–12} twinning,which eventually suppresses the activation of{10–12}twinning.Therefore,in Mg–15Gd,the similar area fractions of twinning-possible grains under tension and compression and the enhanced slip and suppressed twinning caused by the abundant Gd solute atoms lead to a gradual decrease in the strain hardening rates in both the tension and compression tests.

4.2. Variations in slip and twinning behaviors and yield asymmetry with Gd addition

As mentioned in Section 4.1,Gd addition to pure Mg considerably affects the slip and twinning behaviors of the extruded material.Moreover,as the amount of Gd added to pure Mg increases from 0 to 15 wt%,the yield asymmetry of the extruded material decreases drastically,as evidenced by the increase in CYS/TYS from 0.4 to 1.2.Variations in the activities of the various deformation modes with Gd addition are quantitatively analyzed to elucidate the influence of Gd addition on the deformation behaviors and yield asymmetry of the extruded material.The addition of RE elements to Mg alloys is known to change the CRSSs of basal slip,prismatic slip,pyramidal slip,and {10–12} twinning (hereafter denoted as CRSSbasal,CRSSprismatic,CRSSpyramidal,and CRSStwinning,respectively) via the dislocation binding effect of solute atoms [44] and a decrease in thec/aratio [20].According to previous studies,the CRSSpyramidal/CRSSbasal,CRSSprismatic/CRSSbasal,and CRSStwinning/CRSSbasalratios of pure Mg are approximately 35,7.8 and 2.1,respectively[45,46],whereas the corresponding ratios of Mg–15Gd are lower,2.2,2.1 and 1.2,respectively [18].

The plastic deformation of a metallic material at RT occurs by dislocation slip and/or deformation twinning,and the stress required for the activation of these deformation modes is calculated by dividing the CRSS by the SF (i.e.,activation stress=CRSS/SF).In particular,at the yield point,i.e.,the point at which the plastic deformation begins,the deformation mode with the lowest activation stress is activated first.Therefore,it is important to compare the activation stresses of all possible deformation modes of extruded materials to determine the variation in the TYS and CYS with Gd addition.Figs.9–11 show the grain distributions (bar graph) and calculated relative activation stresses of basal slip,prismatic slip,pyramidal slip,and {10–12} twinning (line graph) as functions ofθunder tension and compression for pure Mg,Mg–5Gd,and Mg–15Gd,respectively.The prismatic poles of the extruded materials are broadly distributed in their (10–10)PFs (Fig.6a–c),which suggests that the angle between theaaxes of grains and the loading axis(denoted asα)is randomly distributed in the range of 0°–30°[41].Hence,the relative activation stresses in Figs.9–11 are calculated by averaging the maximum and minimum relative activation stresses over anαrange of 0°–30°.On the basis of results of previous studies,the CRSSbasal/CRSSpyramidal/CRSSprismatic/CRSStwinningratio is taken as 1:35:7.8:2.1 for pure Mg [45,46] and 1:2.2:2.1:1.2 for Mg–15Gd [18] to calculate the relative activation stresses.To the best of our knowledge,no study has yet reported on the CRSS ratio of the deformation modes in Mg–5Gd.Hence,under the assumption that the CRSS of each deformation mode varies linearly with the Gd content,the CRSS ratio of the deformation modes in Mg–5Gd is arithmetically obtained from those in pure Mg and Mg–15Gd.The CRSS ratio of the deformation modes in Mg–5Gd is obtained as 1:6.8:2.9:1.3,and this ratio can be considered effective in the analysis of the relative activation stresses of slip and twinning because the mechanical properties of Mg alloys vary almost linearly with the content of the added RE element [8,15,22].Tables 2–4 present theθranges of regions with the lowest activation stresses of the various deformation modes,their area fractions,and their average SF values—all obtained from Figs.9–11—for pure Mg,Mg–5Gd,and Mg–15Gd,respectively.

When pure Mg is subjected to tensile loading along the ED(Fig.9a and Table 2),grains withθlower than 14° constitute a twinning-favorable region (red shaded area in Fig.9a),in which the activation stress of {10–12} twinning is the lowest among the four activation stresses.Note that because the relative activation stress of pyramidal slip is substantially higher than those of the other deformation modes,its relative activation stress curve is not presented in Fig.9a and b.Because thec-axes of most grains in pure Mg are aligned perpendicular to the loading direction (ED),no twinning-favorable grains are present in pure Mg under tension.Grains with a large area fraction of 77.4% constitute a basal-slip-favorable region withθin the range of 14°–86.5° (black shaded area in Fig.9a),and grains with an area fraction of 22.6% constitute a prismatic-slip-favorable region withθhigher than 86.5°(blue shaded area in Fig.9a).Contrarily,when pure Mg is subjected to compressive loading along the ED (Fig.9b and Table 2),grains with a large area fraction of 53.7% constitute a twinning-favorable region (θ>77.5°),whereas the remaining grains (i.e.,with an area fraction of 46.3%) constitute a basal-slip-favorable region (0° <θ<77.5°).Therefore,in pure Mg,grains withθof >86.5° accommodate plastic deformation via prismatic slip under tension and those withθof>77.5°accomodate plastic deformation via{10–12}twinning under compression.Because the CRSS of prismatic slip is approximately four times that of {10–12} twinning,the minimum activation stress of the former is significantly higher than that of the latter (atθ=90°,the relative activation stress of prismatic slip under tension is 16.8,whereas that of {10–12} twinning under compression is 4.9;Fig.9).Consequently,the TYS of pure Mg is significantly higher than its CYS despite the similar average SF values for prismatic slip and {10–12} twinning (0.47 and 0.44,respectively;Table 2).Asθincreases or decreases from 45°,the activation stress of basal slip increases (black lines in Fig.9a and b)owing to a decrease in its SF value.The maximumθof the basal-slip-favorable region under compression(77.5°;Fig.9b)is lower than that under tension (86.5°;Fig.9a).Therefore,under compression,the basal-slip-favorable region has a relatively high average SF value(0.28),and the relative activation stress of the active deformation mode for all grains is lower than 5.5,which consequently results in a low average relative activation stress of pure Mg under compression (3.7).In contrast,under tension,because only grains withθhigher than 86.5° (area fraction: 22.6%) can accommodate deformation via prismatic slip,some grains withθclose to 86.5° have a low SF value for basal slip and the relative activation stress of basal slip for these grains is required to be as high as 17.0.Consequently,the entire basal-slip-favorable region under tension has a lower average SF value (0.22) than that under compression (0.28) and the average relative activation stress of pure Mg under tension is as high as 9.0,which is 2.4 times that under compression(3.7).These results indicate that the stress required for yielding under tension is considerably higher than that under compression.The minimum relative activation stress of pyramidal slip is as high as 70.0 atθof 15° and the relative activation stress of pyramidal slip is higher than that of basal slip,prismatic slip,or {10–12} twinning over the entireθrange.This suggests that pyramidal slip is not activated under both tension and compression in pure Mg.Therefore,in pure Mg,the significantly higher CRSS of prismatic slip than of {10–12} twinning—which are activated under tension and compression,respectively—and the higher average activation stress of basal slip of grains under tension result in a considerable difference between the CYS and the TYS (39.5 and 112.4 MPa,respectively) and consequently high yield asymmetry (CYS/TYS=0.4).

Table 2Characteristics of regions with lowest activation stress of each deformation mode under tension and compression along ED for pure Mg.

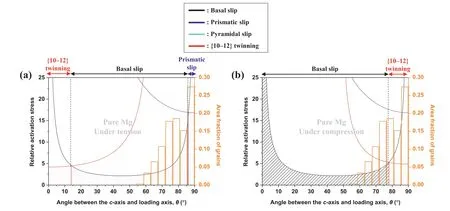
Fig.9.Relative activation stresses (=CRSS/SF) of basal slip,prismatic slip,pyramidal slip,and {10–12} twinning under (a) tension and (b) compression along ED and area fraction of grains as a function of angle θ between c-axis and loading axis for pure Mg.The relative activation stress is calculated by dividing the CRSS by the SF.In the calculation of all the relative activation stresses,the ratio of the CRSSs of basal slip,prismatic slip,pyramidal slip,and{10–12} twinning is considered to be 1:7.8:35:2.1.Since the relative activation stress of pyramidal slip is substantially high (>70) as compared to those of basal slip,prismatic slip,and {10–12} twinning,the relative activation stress curve of pyramidal slip is not presented in (a) and (b).

Fig.10a and b shows the variations in the relative activation stresses of Mg–5Gd withθunder tension and compression,respectively.The minimum relative activation stress of pyramidal slip in Mg–5Gd is considerably lower as 13.6 atθof 15°than that in pure Mg(70.0 atθof 15°).However,pyramidal slip is not activated under tension because its relative activation stress is higher than those of the other slip systems and {10–12} twinning over the entireθrange (Fig.10a).Under compression,the relative activation stress of pyramidal slip is the lowest among the four deformation mechanisms in the grains withθlower than 4.6° (Fig.10b).However,these pyramidal-slip-favorable grains whoseθranges from 0° to 4.6° are absent in Mg–5Gd;therefore,pyramidal slip is not activated under compression as well as under tension.As mentioned earlier,the Gd solute atoms decrease the CRSSprismatic/CRSSbasalratio;therefore,theθrange of the prismatic-slip-favorable region in Mg–5Gd under tension (80.5°–90.0°) is wider than that in pure Mg under tension (86.5°–90.0°).However,because the Gd present in Mg–5Gd reduces the maximum intensity of the (0001) poles and slightly tilts them toward the ED (Fig.6b),the area fraction of grains within the prismatic-slip-favorable region (25.0%) is not greatly different from that in pure Mg (22.6%),and the SF value for prismatic slip of these grains is the same as that in pure Mg (0.47) (Fig.10a and Table 3).In Mg–5Gd,grains withθof >80.5° accommodate deformation via prismatic slip under tension and those withθof >73.0° accomodate deformation via {10–12} twinning under compression.However,a decrease in the CRSSprismatic/CRSStwinningratio causes a decrease in the difference between the relative activation stresses of prismatic slip and {10–12} twinning.Therefore,such grains with highθrequire similar activation stresses under both tension and compression,which contributes to a decrease in the yield asymmetry of Mg–5Gd.Additionally,because of the widerθrange of the prismatic-slip-favorable region under tension in Mg–5Gd,theθrange of the basalslip-favorable region in this material(22.5°–80.5°)is narrower than that in pure Mg (14.0°–86.5°).This widerθrange of the prismatic-slip-favorable region also reduces the area fraction of grains with low SF values for basal slip under tension (especially grains withθof >80.0°) and increases the average SF value of the basal-slip-favorable region to 0.35,which is considerably higher than that of pure Mg (0.22).Because of the higher SF value of the basal-slip-favorable region under tension,the average relative activation stress of basal slip under tension (3.3) is similar to that under compression (2.6),which consequently results in the low yield asymmetry of Mg–5Gd.Therefore,as a result of the combined effect of the decrease in the relative activation stress of prismatic slip and the comparable average activation stresses of the basalslip-favorable region under tension and compression,Mg–5Gd exhibits superior yield symmetry (CYS/TYS=0.9) to pure Mg (CYS/TYS=0.4).

Table 3Characteristics of regions with lowest activation stress of each deformation mode under tension and compression along ED for Mg–5Gd.

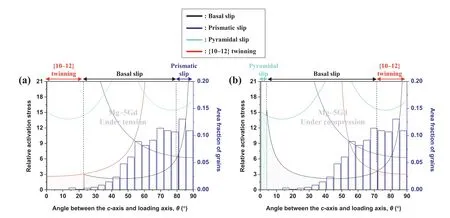
Fig.10.Relative activation stresses of basal slip,prismatic slip,pyramidal slip,and {10–12} twinning under (a) tension and (b) compression along ED and area fraction of grains as a function of θ for Mg–5Gd.In the calculation of all the relative activation stresses,the ratio of the CRSSs of basal slip,prismatic slip,pyramidal slip,and {10–12} twinning is considered to be 1:2.9:6.8:1.3.

The main deformation modes in grains with highθin Mg–15Gd (Fig.11 and Table 4) are identical to those in the other two materials: prismatic slip in grains withθof >76.5° under tension and {10–12} twinning in grains withθof >70.5° under compression.Their average SF values are also as high as 0.47 and 0.42,respectively (Table 4).However,because the CRSSprismatic/CRSSbasalratio (2.1) and CRSStwinning/CRSSbasalratio (1.2) of Mg–15Gd are lower than those of Mg–5Gd(2.9 and 1.3,respectively),the difference between the lowest relative activation stresses of prismatic slip under tension and {10–12} twinning under compression is smaller in Mg–15Gd (atθ=90°,the relative activation stress of prismatic slip under tension is 4.5 and that of {10–12} twinning under compression is 2.7;Fig.11) than in Mg–5Gd (atθ=90°,the relative activation stress of prismatic slip under tension is 6.2 and that of {10–12} twinning under compression is 3.0;Fig.10),thereby reducing the yield asymmetry of Mg–15Gd.Although the decrease in the CRSSprismatic/CRSSbasalratio causes an increase in the CYS/TYS ratio of Mg–15Gd,prismatic slip still has a higher activation stress than {10–12} twinning.Therefore,additional factors contribute to the higher CYS of Mg–15Gd than its TYS.Park et al.[47] reported that even a cast AZ31 alloy with a random texture exhibits tension–compression yield asymmetry,which originates from the different characteristics of the SF value for twinning under tension and compression.Under tension,the maximum average SF value for {10–12} twinning is 0.499(atθ=0°) and it decreases gradually with increasingθ;in contrast,under compression,the maximum average SF value for {10–12} twinning is 0.437 (atθ=90°) and it decreases sharply with decreasingθ[47].In the present study,Mg–15Gd has similar area fractions of twinning-favorable grains under tension and compression (22.1% and 29.9%,respectively;Table 4).However,the SF value of twinning-favorable grains under compression (0.42) is lower than that under tension (0.46) (Table 4),which is consistent with previously reported results [47].Because of this lower SF value for twinning under compression,the relative activation stress of twinning under compression is higher than that under tension;this behavior consequently contributes to the occurrence of reversed yield asymmetry of Mg–15Gd (CYS/TYS=1.2).Additionally,in all the extruded materials,whenθdecreases from 45° to 0°,the SF value for basal slip decreases substantially,and accordingly,the relative activation stress of basal slip increases rapidly.Although the CRSSpyramidal/CRSSbasalratio considerably decreases to 2.2 in Mg–15Gd,the relative activation stress of pyramidal slip under tension is still higher than those of the other deformation modes at allθvalues (Fig.11a),which suggests that pyramidal slip is not activated under tension in Mg–15Gd,as with pure Mg and Mg–5Gd.In contrast,under compression,the relative activation stress of pyramidal slip in Mg–15Gd is the lowest among the four deformation mechanisms in grains withθof <14.5° (Fig.11b),and theθrange of the pyramidal-slipfavorable region in Mg–15Gd (0°–14.5°) is wider than that in Mg–5Gd (0°–4.6°).Furthermore,because of the evenly distributed crystallographic orientations of grains in Mg–15Gd,the pyramidal-slip-favorable grains whoseθranges from 0°to 14.5° under compression are present in Mg–15Gd (with an area fraction of 9.4%) and they have a high average SF value for pyramidal slip of 0.49 (Table 4),which suggests that pyramidal slip occurs under compression in Mg–15Gd,unlike the other two materials.The area fraction of the basalslip-favorable grains under tension (56.3%) is similar to that under compression (60.7%),and these grains have the same average SF value (0.40) for basal slip under both tension and compression (Table 4).However,because of the difference in theθrange of the basal-slip-favorable region under tension and compression(Fig.11),the average relative activation stress of the basal-slip-favorable grains under compression(2.82) is higher than that under tension (2.69).In addition,the area fraction of the {10–12} twinning-favorable grains under compression (29.9%) is higher than that under tension(22.1%),and their average SF value for {10–12} twinning is lower under compression (0.42) than under tension (0.46)(Table 4);consequently,the average relative activation stress of the {10–12} twinning-favorable grains under compression(2.86) is higher than that under tension (2.61).These higher average activation stresses of basal slip and {10–12} twinning under compression lead to the higher CYS of Mg–15Gd than its TYS.Therefore,Mg–15Gd exhibits reversed yield asymmetry (CYS/TYS=1.2),unlike pure Mg and Mg–5Gd.

Table 4Characteristics of regions with lowest activation stress of each deformation mode under tension and compression along ED for Mg–15Gd.

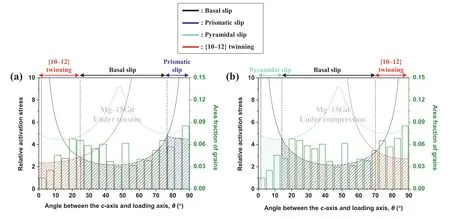
Fig.11.Relative activation stresses of basal slip,prismatic slip,pyramidal slip,and {10–12} twinning under (a) tension and (b) compression along ED and area fraction of grains as a function of θ for Mg–15Gd.In the calculation of all the relative activation stresses,the ratio of the CRSSs of basal slip,prismatic slip,pyramidal slip,and {10–12} twinning is considered to be 1:2.1:2.2:1.2.

4.3. Microstructural and textural variations during tensile and compressive deformation

Fig.12 shows IPF maps of the fractured tensile and compressive specimens of the extruded materials.In the IPF maps of the fractured tensile pure Mg and Mg–5Gd specimens,most grains are blue or green (Fig.12a and b),which is similar to the colors in the IPF maps of pure Mg and Mg–5Gd before tension (Fig.5).The insignificant change in color on the IPF maps after tension suggests that the dislocation slip predominantly occurs under tension because {10–12} twinning causes a drastic color change in the IPF map as a result of the lattice reorientation.Moreover,in the blue and green grains,sharp twins are observed in the fractured tensile pure Mg and Mg–5Gd specimens,and their morphology corresponds to the crack-initiated twins observed in their optical images (Fig.3a and b).These twins are {10–11} contraction twins or {10–11}-{10–12} double twins because they are formed in the blue and green grains,which are subjected toc-axis contraction stress under tension.As these contraction and double twins are formed in the late stage of tensile deformation owing to their high CRSSs [30],their formation does not affect the TYSs of pure Mg and Mg–5Gd.In the fractured tensile Mg–15Gd specimen,red grains are present on the IPF map along with blue and green grains (Fig.12c).Moreover,relatively thick twins with blue or green color are formed in almost all the red grains,whereas no twins are formed in the blue and green grains.The red grains with basal poles aligned nearly parallel to the ED are subjected toc-axis extension stress under tension;therefore,{10–12}twins are formed in the red grains in the early stage of tensile deformation.Therefore,in Mg–15Gd,dislocation slip occurs in the blue and green grains and {10–12} twinning occurs in the red grains under tension.Consequently,dislocation slip predominantly occurs in pure Mg and Mg–5Gd and both dislocation slip and {10–12} twinning occur in Mg–15Gd during tensile deformation;this result is consistent with the analysis results of relative activation stresses under tension(Figs.9a–11a).

Fig.12.IPF maps of fractured tensile and compressive specimens of (a) pure Mg,(b) Mg–5Gd,and (c) Mg–15Gd.

After the compressive test,the color on the IPF map of pure Mg and Mg–5Gd changes from blue and green to red,which indicates that {10–12} twins are formed throughout the materials under compression.Under compression along the ED,the blue and green grains with basal poles aligned nearly perpendicular to the ED are favorable for {10–12}twinning because they are subjected to thec-axis extension stress.{10–12} twins are formed in a blue or green grain in the early stage of compressive deformation and they grow during further deformation;consequently,the twins occupy the entire grain area and the fully twinned grain is red color.In Mg–15Gd,when compared its IPF maps before and after compression(Figs.5c and 12c),the area fraction of red grains also increases after compression because of the formation of{10–12} twins in the blue and green grains.However,unlike in pure Mg,some green or yellow grains are still present after compression in Mg–15Gd,and in these non-twinned grains,dislocation slip occurs under compression.The area fraction of grains that are not red (i.e.,green or yellow grains) in the fractured compressive specimens is in the order of Mg–15Gd>Mg–5Gd >pure Mg (Fig.12).This order indicates that the degree of activation of dislocation slip during compressive deformation of the extruded material increases with increasing Gd content,which is consistent with the analysis results of relative activation stresses under compression (Figs.9b–11b).

Fig.13 shows the (0001) PFs and orientation distributions of grains as a function ofθfor the fractured tensile and compressive specimens of the extruded materials.In pure Mg and Mg–5Gd,{10–12} twinning rarely occurs under tension because the area fractions of twinning-possible grains under tension are significantly low (0.0% and 5.9%,respectively;Fig.8a and b).Therefore,the (0001) PFs after tension of pure Mg and Mg–5Gd are comparable to those before tension (Fig.6a and b),and the orientation distributions of grains after tension also have similar tendencies to those before tension;namely,the area fraction of grains increases with increasingθin both specimens before and after tension(Fig.13a and b).It is predicted from the analysis of relative activation stresses (Figs.9a and 10a) that in pure Mg and Mg–5Gd,most of the tensile strain is accommodated via basal slip.If dislocation slip occurs in a grain,the slip plane of the grain gradually rotates to align parallel to the tensile axis owing to the lattice constraint between the grains [48].Accordingly,when basal slip occurs under tension along the ED in the extruded materials,thec-axes of the grains rotate to align perpendicular to the ED,resulting in an increase in the area fraction of grains with highθ.In both pure Mg and Mg–5Gd,the area fraction of grains with highθincreases after tension;consequently,the averageθof pure Mg and Mg–5Gd increases from 78.7° to 79.9° and from 68.6° to 75.8°,respectively.This result implies that basal slip predominantly occurs under tension in pure Mg and Mg–5Gd,and the degree of activation of basal slip is much more pronounced in Mg–5Gd.This is consistent with the activation stress analysis result that the average relative activation stress of basal slip under tension is considerably lower in Mg–5Gd (3.3) than in pure Mg (9.0).Unlike pure Mg and Mg–5Gd,the (0001) PF of Mg–15Gd significantly changes after tension (Fig.13c),which is mainly attributed to the lattice reorientation by {10–12} twinning in the ED-oriented grains (i.e.,red grains on the IPF map) under tension.As a result,the area fraction of grains withθlower than 45°decreases,whereas that of grains withθhigher than 45° increases after tension in Mg–15Gd(Fig.13c),resulting in an increase in the averageθfrom 49.2°to 63.2°.The fractured compressive specimens of all the extruded materials exhibit similar (0001) PFs with ED-oriented basal poles regardless of their initial texture,and all the specimens have a high area fraction of grains withθof <45° and a low area fraction of grains withθof >45°.These crystallographic orientations of the fractured compressive specimens mainly result from the occurrence of {10–12} twinning in the non-ED-oriented grains(i.e.,blue and green grains on the IPF map) under compression.Under tension and compression,the{10–12} twinning behaviors in the three extruded materials are consistent with their area fractions of twinning-possible grains (Fig.8) and theθranges of regions with low activation stress for {10–12} twinning (Figs.9–11).

When dislocation slip is activated,dislocation gliding induces lattice incompatibility,which generates lattice rotation and in-grain misorientation [49].The rotation axes (disorientation axes) of in-grain misorientation vary with the active dislocation slip system: the disorientation axes of basal slip,prismatic slip,and pyramidal slip are,<0001>,anddirections,respectively [49].Fig.14 shows the distributions of the disorientation axes of low-angle grain boundaries with misorientations ranging from 0.5° to 2.0° of the fractured tensile and compressive specimens of the extruded materials.In pure Mg,disorientation axes are strongly distributed in direction in both tensile and compressive specimens (Fig.14a),which indicates the activation of basal slip and/or pyramidal slip under tension and compression.Because the CRSS of pyramidal slip is substantially higher than that of basal slip in pure Mg (CRSSPyramidal/CRSSBasal=35),the occurence of pyramidal slip in this material is difficult.Wei et al.[50] observed dislocation behavior under RT tension in pure Mg using transmission electron microscopy,and reported that only basal slip is activated in coarse grains because of the low flow stress imposed on the grains.Therefore,it is considered that basal slip predominantly occurs under tension and compression in pure Mg when only dislocation slip systems are taken in to account,except twinning.As described in Section 4.2,the relative activation stress of basal slip is the lowest among the slip systems in most grains under both tension and compression(Fig.9),which is consistent with the strong disorientation axes in pure Mg.Although {10–12} twinning vigorously occurs under compression in pure Mg,the influence of twinning on the disorientation axis distribution is negligible because only low-angle grain boundaries (0.5°–2.0°) are considered in the disorientation axis analysis and the misorientation of {10–12} twin boundaries is as high as 86.3°.

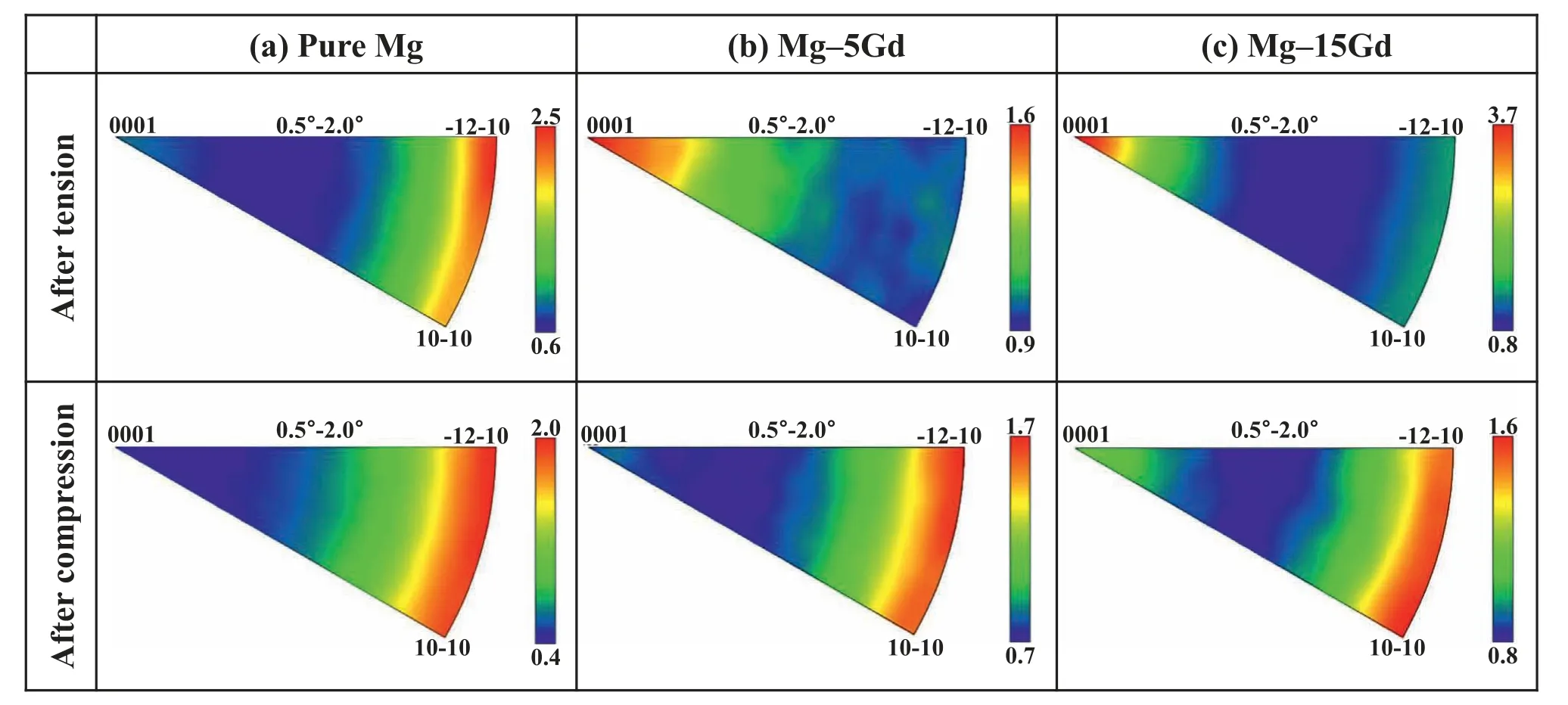
Fig.14.Disorientation axis distributions of fractured tensile and compressive specimens of (a) pure Mg,(b) Mg–5Gd,and (c) Mg–15Gd.

In Mg–5Gd,the disorientation axis distributions of the tensile and compressive specimens are significantly different(Fig.14b).According to the relative activation stress analysis results of Mg–5Gd (Fig.10a and Table 3),basal slip can be activated in a large amount (area fraction: 74.5%) of grains and prismatic slip can also be activated in some grains (area fraction: 25.0%) under tension.The tensile Mg–5Gd specimen has a strong <0001>disorientation axis,which implies activation of prismatic slip under tension.Although the intensity of disorientation axis distributions is the highest in<0001>direction,the disorientation axes are also present in large amounts,as evidenced by the highest minimum scale level of 0.9 among the three tensile specimens.This implies that basal slip also actively occurs under tension in Mg–5Gd.Moreover,as shown in Fig.13b,as the tensile deformation progresses,thec-axes of grains are rotated toward the direction perpendicular to the ED owing to basal slip activation,which subsequently results in gradual increases in the SF for prismatic slip of the grains and the area fraction of prismatic-slip-favorable grains.Consequently,the intensity of the <0001>disorientation axis corresponding to prismatic slip is relatively strong in the fractured tensile specimen.Under compression,{10–12} twinning and basal slip are the main deformation mechanisms of Mg–5Gd (Fig.10b);therefore,only strong disorientation axes appear in the compressive Mg–5Gd specimen (Fig.14b).In Mg–15Gd,the disorientation axes are distributed in <0001>and directions in the tensile specimen,which implies the activation of both basal slip and prismatic slip under tension.Unlike the other compressive specimens,the compressive Mg–15Gd specimen has not only strong disorientation axes but also a weak <0001>disorientation axis;this result suggests that prismatic slip occurs to a certain degree under compression in Mg–15Gd,as well as basal slip and pyramidal slip.This activation of prismatic slip under compression in Mg–15Gd can be attributed to the smaller difference in the minimum relative activation stresses of prismatic slip and{10–12} twinning in Mg–15Gd (1.8) compared to the differences in pure Mg (11.9) and Mg–5Gd (3.2).The overall active deformation mechanisms under tension and compression of the extruded materials discussed in this section based on the EBSD results of the fractured specimens agree well with the analysis results of the relative activation stresses of deformation modes in Section 4.2.

5.Conclusions

This study investigates the Gd-addition-induced evolutions of the strain hardening behavior and tension–compression yield asymmetry of extruded pure Mg.Pure Mg,Mg–5Gd,and Mg–15Gd all have fully recrystallized grain structures.However,the average grain sizes of Mg–5Gd and Mg–15Gd are significantly smaller than that of pure Mg because of the solute drag effect of Gd solute atoms.As the Gd content increases from 0 to 15 wt%,the basal texture of the extruded material tilts toward the ED,and the average deviation angle of the (0001) poles from the ED decreases from 78.7° to 49.2°.Because most grains in pure Mg and Mg–5Gd have crystallographic orientations conducive to the activation of{10–12} twinning under compression,both the materials exhibit twinning-and slip-dominant deformation behaviors in compression and tension tests,respectively.In contrast,Mg–15Gd exhibits slip-dominant deformation behavior under both tension and compression because of the uniformly distributed orientations of grains and the promoted prismatic slip and suppressed {10–12} twinning during deformation.Pure Mg,having a strong basal texture,exhibits substantially high yield asymmetry (CYS/TYS=0.4) because of the large difference between the activation stresses of prismatic slip and twinning and the difference between the activation stresses of basal slip under tension and compression.Mg–5Gd,having a tilted basal texture,exhibits excellent yield symmetry (CYS/TYS=0.9)owing to the Gd solute atom–induced decrease in the difference between the CRSSs of prismatic slip and twinning and the comparable average SF values of basal-slip-favorable grains under compression and tension.Mg–15Gd,having an ED-oriented basal texture,exhibits reversed yield asymmetry(CYS/TYS=1.2),which is attributed to the combined effects of the further decrease in the CRSS difference between prismatic slip and twinning and the higher average activation stresses of basal slip and twinning under compression than under tension.The EBSD results of the fractured tensile and compressive specimens of the extruded materials confirm the different active deformation mechanisms under tension and compression in pure Mg,Mg–5Gd,and Mg–15Gd,which are consistent with the analysis results of the relative activation stresses of deformation modes.

Declaration of competing interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This research was supported by the National Research Foundation of Korea (NRF) grant (No.2019R1A2C1085272)funded by the Ministry of Science,ICT and Future Planning(MSIP,South Korea).