烟盒围条折弯过程的显示动力学仿真分析

肖帅

（武汉轻工大学 机械工程学院，武汉 430023）

0 引言

随着我国科学技术的发展，以及人们对健康越来越重视，国家对各烟企提出了提质减量的要求，使得天地盖烟盒新型包装快速发展。天地盖烟盒由上盖、下盖、围条、面纸4部分构成，如图1所示[1]。

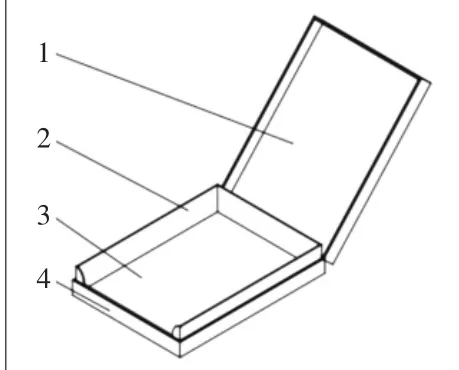
图1 天地盖烟盒

生产中，围条折弯时，折痕处易出现应力集中超过耐破强度，从而导致围条撕裂，围条纸厚、折弯转速、折弯位置等要素对围条的折弯成型质量有着重要影响。

1 纸张变形过程仿真应用

虚拟仿真技术在纸张变形领域应用非常广泛，周廷美等[2]基于ANSYS APDL对瓦楞纸箱成型过程进行非线性有限元分析，得到瓦楞纸板折弯时的应力变化图及折叠力矩，为瓦楞纸板成型工艺提供了参考；王越等[3]基于内聚区模型，对纸张的剪切过程进行仿真分析，给出了确定纸张剪切内聚区模型关键参数的方法。

纸张变形的仿真算法分为：显式算法和隐式算法。显式算法基于动力学方程，采用一些差分格式（如中心差分法、线性加速度法等），不需要平衡迭代，一般不存在收敛性的问题。隐式算法在每一个增量步内都需要对静态平衡方程进行迭代求解，运用到高度非线性问题时无法保证收敛性[4]。从力学角度分析，本次围条折弯过程属于一个大位移、大变形的过程，涉及几何非线性、材料非线性问题，故本次采用ANSYS Workbench/ Explicit Dynamics显示动力模块进行仿真分析。

该模块采用中心差分时间积分方案，在网格节点处计算出力之后，加速度计算公式为

式中：xi″为节点加速度组成部分；Fi为节点力；bi为节点加速度；m为节点质量分布。

当加速度在n时刻确定，n+1/2时刻的加速度积分可以表示为

故n+1时刻的加速度积分表示为

2 围条折弯过程仿真分析

2.1 围条材料

围条的材料是定量400 g/m2、厚度0.56～0.58 mm的白卡纸，密度为714.28 kg/m3，耐破强度为0.48 MPa，呈长方体形态，表面有4条压痕线，如图2所示。

图2 围条结构

此类白卡纸，属于一种各向异性的材料，其各种性能指标如表1所示。由于围条厚度过小，有些参数较难测量，故在实验中只需测出Ex、νxy、νxz、νyz，根据以下公式近似得出其余的物理量[5]：

表1 围条性能参数

2.2 围条折弯过程仿真前处理

围条实际生产过程中折弯步骤如图3所示，围条经两次折弯形成围合，围条在一次折弯时折痕处易出现撕裂现象。

图3 围条折弯步骤

本文对围条进行一次折弯仿真，具体模型如图4所示。

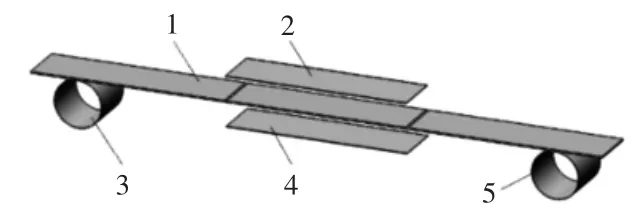
图4 折弯模型

将上述三维模型导入，定义围条材料，将围条定义为柔性；其余结构采用结构钢，定义为刚性。

围条折弯过程的接触行为主要是面与面的接触，将刚性面设置为“目标面”，柔性面设置为“接触面”，接触行为设置为非对称接触[6]。接触类型为摩擦接触，摩擦因数设置为0.3。

网格划分对于有限元仿真分析至关重要，直接影响仿真结果的精确度[7]。折弯模型网格类型采用六面体网格，将折痕附近网格进行细划：折痕处网格尺寸为0.2 mm，其余部分网格尺寸为2 mm，如图5所示。

边界条件的设置，主要包括对各个结构的移动限制，具体动作为：1）压板一沿Z轴正向移动5 mm，压板二沿Z轴负向移动5 mm，实现对围条中部的固定；2）折弯立柱以一定的折弯转速绕折弯中心点Z轴逆时针做1/4圆周运动，对围条进行折弯，如图6所示。

图6 折弯转动副

2.3 仿真结果分析

实际生产情况表明，折弯位置的D直接影响围条折弯效果，具体位置如图7所示。

图7 折弯位置

保持折弯转速一致，改变折弯位置对纸厚0.56、0.57、0.58 mm的围条进行折弯仿真，探究折弯位置对围条折弯过程中最大应力的影响。仿真结果如图8所示，从图中可以得出：在同一折弯转速、位置的情况下，随着围条纸厚的增加，围条折弯过程中最大应力逐渐减小；在同一折弯转速、围条纸厚情况下，改变D值，最大应力变化并无规律。通过观察围条折弯变形效果：折弯位置0～2 mm时，围条不能顺利折弯变形，如图9（a）所示；4～8 mm时，围条顺利折弯，变形效果较好，如图9（b）所示；10 ～20 mm时，围条折弯变形翘曲严重，如图9（c）所示。

图8 折弯位置-最大应力

图9 围条折弯变形图

围条折弯转速的合理选取对折弯质量及折弯效率至关重要，为了探究折弯转速对围条折弯过程中最大应力的影响，保持折弯位置一致，改变折弯转速，对纸厚0.56、0.57、0.58 mm的围条进行折弯仿真，结果如图10所示。从图中可以得出：在同一折弯转速、位置的情况下，随着围条纸厚增加，折弯过程中最大应力逐渐减小；在同一围条纸厚、折弯位置的情况下，随着折弯转速的增加，最大应力逐渐增大。

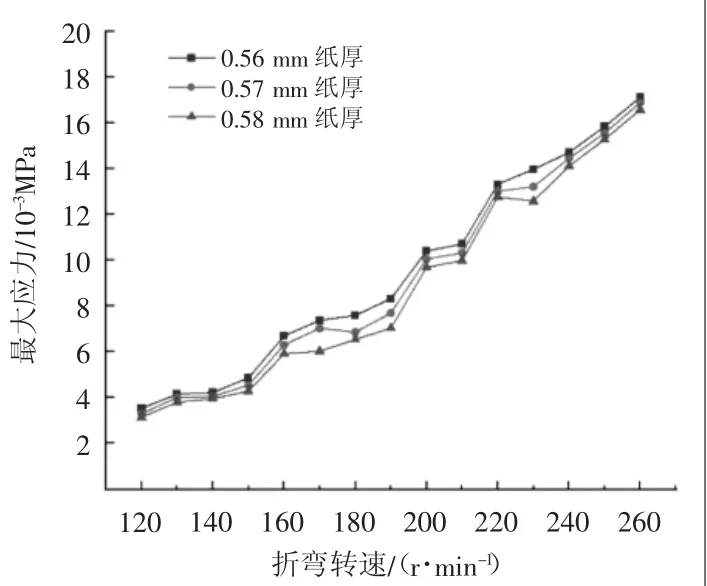
图10 折弯转速-最大应力

3 围条折弯过程参数优化

综合上述仿真结果，利用SPSS数据分析软件进行正交实验设计并进行多因素极差、方差分析[8-9]，影响因素分别为围条纸厚T、折弯转速V、折弯位置D，每个因素3个水平。正交实验因素水平表如表2所示。

表2 因素水平表

按照正交表安排实验方案，对每次实验进行显示动力学仿真，得到围条折弯时的最大应力，将其作为优化指标，最大应力越小越好，正交实验方案及结果如表3所示。

表3 正交实验设计结果

采用SPSS软件进行极差分析，极差分析结果如表4所示。由极差分析结果可以得出，上述3种因素对围条折弯最大应力的影响主次为：折弯转速V>围条纸厚T>折弯位置D；最优方案组合为：T3V1D2。该方案未在正交实验中出现，故导入模型，设置相关参数，进行折弯仿真实验，得到折弯过程中的变形图及应力变化图如图11所示，折弯过程最大应力出现在折痕处，为0.002 12 MPa，强度符合要求。说明：K 值为某因素某水平时试验数据求和；Kavg值为对应的平均值。

图11 最优方案变形应力图

4 结语

本文对天地盖烟盒围条折弯动作进行显示动力学仿真，分析围条纸厚、折弯转速、折弯位置的变化对围条折弯过程中最大应力的影响，主要结论如下：

1）围条折弯过程中，最大应力随围条纸厚的增大而减小，随折弯转速的增大而增大；折弯位置对折弯成型效果影响显著，折弯位置在4～8 mm时，折弯变形效果较好。

2）对围条折弯过程中最大应力影响程度依次为：折弯转速>围条纸厚>折弯位置；最优参数为：围条纸厚0.58 mm、折弯转速120 r/min、折弯位置6 mm，此时围条最大应力为0.002 12 MPa，小于围条耐破强度，满足要求。