基于BA-VMD-LSSVM的超短期电力负荷预测
李吉献,宋启广,刘光宇,陈柏文
(山东电力工程咨询院有限公司,济南 250013)
0 引言
光伏、风电的大规模使用给能源系统带来一定的问题。由于它们具有很强的波动性和随机性,这将会影响发用电端平衡,进而破坏能源系统。因此,高精度的电力负荷预测是至关重要的[1-3]。
目前的电力负荷预测主要分为传统预测和机器学习预测[4]。由于传统预测的数学模型简单,所以其预测精度较低。然而,人工神经网络和支持向量机(SVM)等机器学习预测则具有处理非线性问题的优势,得到了国内外学者的广泛关注。例如,邹超等[5]使用SVM实现对短期负荷的预测。胡乙丹等[6]使用网格算法对SVM的超参数进行优化,完成对短期电力负荷的预测工作。但是,对波动性较大的原始负荷直接进行预测,会严重影响SVM的预测性能。丁宏等[7]首先使用重复小波变换将负荷数据分解为若干子序列,然后应用SVM进行处理,达到了不错的预测精度。小波变换需要根据经验选择小波基函数,会影响模型的自适应性。此外,与SVM相比,最小二乘支持向量机(LSSVM)可快速进行优化参数和预测等操作。胡文波等[8]使用变分模态分解(VMD)降低负荷波动性的影响,随之应用混沌鲸鱼优化的LSSVM进行预测,取得了不错的预测结果。赵凤展等[9]使用VMD分解负荷数据,随后使用蝙蝠算法(BA)优化的LSSVM进行负荷预测,有效提高了预测精度。但是,它们未考虑到VMD的参数设置,在一定程度上将影响最终预测结果。
针对上述研究背景,本文提出一种基于BA-VMDLSSVM的超短期负荷预测模型。该模型使用VMD将负荷数据分解,以降低波动性的影响,为LSSVM的下一步预测工作提供良好的数据基础。而且,还使用BA算法对VMD和LSSVM的参数进行全局优化,以进一步改善预测结果。将提出的模型应用于2016年电工数学建模竞赛数据A题地区1的部分真实负荷数据,证实了提出模型预测超短期负荷的高性能。
1 算法介绍
1.1 VMD分解算法
VMD在2014年被提出,随后便被广泛应用于信号处理领域[9-11]。VMD能够克制模态混叠和端点效应,具体步骤如下。
1)假设分解得到的各本征模态函数中心频率不同,即将原问题转化为变分问题。约束条件为:
式中:K为模态分量总数;{uk}为k个模态分量;{ωk}为相应中心频率;δ(t)为狄拉克分布;f(t)为时间序列;t为采样点。
2)引入增广Lagrange函数,转化为非约束变分问题,公式为
式中:λ为拉格朗日乘子;α为惩罚因子。
3)通过交替乘子法求解上述问题,迭代更新公式为:
式中:∧代表傅里叶变换;n为迭代次数;τ为保真系数。
通过上述转换,完成对变分问题的求解。
1.2 LSSVM预测算法
LSSVM不仅具有结构风险最小化和小样本等优点,还具有较低的计算复杂度[12]。LSSVM的回归函数为
式中:ω为权重;b为偏差;x为输入数据。
他们对此类产品的需求特征主要体现为以下几点:①在产品的定位上,要做符合大学生心理的产品,不同大学生对于手机的定位也是不同的,有的将其视为身份的象征,有的视为娱乐工具,有的则仅视为通讯工具。②在手机推广宣传上,可通过多种渠道进行轰炸式宣传,利用明星效应,请知名影星做产品的形象代言,增强产品的吸引力。③在产品外形设计上,着重开发新的款式和外观;在功能上,要注重实用性,优化学生用户使用手机的体验感。
式(7)对应的优化问题可用式(8)和式(9)表示:
式中:γ为正则化参数;ei为误差变量。
对上式进行求解,构造拉格朗日函数如下:
式中,αi为拉格朗日乘子。
对式(10)进行偏微分处理,求解α和b,得到的最终回归函数为
式中,K(x,xi)为核函数。
LSSVM核函数为径向基函数,公式为
1.3 BA优化算法
蝙蝠优化算法是新兴的群智能优化算法,其通过模仿蝙蝠的超声波回声定位捕食过程来寻找全局最优解[13]。
假设蝙蝠i在d维空间飞行,其在t+1时刻的速度和位置按照式(13)~式(15)更新:
为提高优化性能,BA算法为最优解添加扰动,如式(16)所示:
式中:ε为区间[0,1]的随机数;At为平均响度。
当寻得最优解后,蝙蝠将降低脉冲响度,提升脉冲频率,迭代更新公式如下:
2 BA-VMD-LSSVM预测模型
负荷数据波动性强,直接对其进行处理将导致预测结果精度较低。本文中使用VMD将负荷数据分解为多个平稳性较强的IMF分量,然后分别使用LSSVM进行处理,并随之执行叠加操作。VMD需设置IMF分量数目k和惩罚因子α,LSSVM需设置惩罚系数γ和核函数宽度σ。而且,负荷预测也需设置时间点数tau。由于上述设置参数会直接影响最终结果,于是本文使用BA算法对上述参数进行全局优化,进而充分发挥VMD的分解能力和LSSVM的预测能力,以保证预测结果达到预期。此外,本文还使用式(19)来全面评价模型优劣:
式中:MAPE为平均绝对百分比误差;RMSE为均方根误差;MAE为平均绝对误差;yi为真实值;y^i为预测值。基于BA-VMD-LSSVM的预测模型流程如图1所示。

图1 BA-VMD-LSSVM预测模型流程图
3 实例分析
实验数据选取2016年电工数学建模竞 赛A 题 中 地 区1 的2014年11月1日至2014年12月30日的真实负荷数据[14],其中,数据间隔为15 min,共计5760个数据点(前4608个数据为训练集,后1152个数据为测试集)。
通过分析处理训练集数据,寻优得到VMD和LSSVM的最优参数。BA算法的参数设置如下:寻优参数数目设置为5,迭代次数设置为10,种群大小设置为30。VMD的k范围设置为[2,10],α范围设置为[500,3000]。LSSVM的参数γ范围设置为[0.01,100],参数σ范围设置为[0.01,100]。负荷预测的时间点数tau范围设置为[2,15]。最优预测参数如表1所示。

表1 最优预测参数表
将VMD参数设置为寻优所得参数,对负荷数据进行分解,以直观地观察其分解能力。部分负荷数据及相应模态分量如图2所示。由图可知,VMD分解得到的IMF分量存在于一定频率范围内,这降低了数据的波动性,有利于进行后续处理。

图2 部分负荷数据及相应模态分量
使用BA优化后的LSSVM对各IMF分量分别进行处理,并执行相加操作得到最终的负荷预测结果。 BA -VMD -LSSVM预测结果如图3所示。由图3可知,BA-VMD-LSSVM 可以较为精准地预测超短期负荷变化情况,证明了提出模型的有效性。
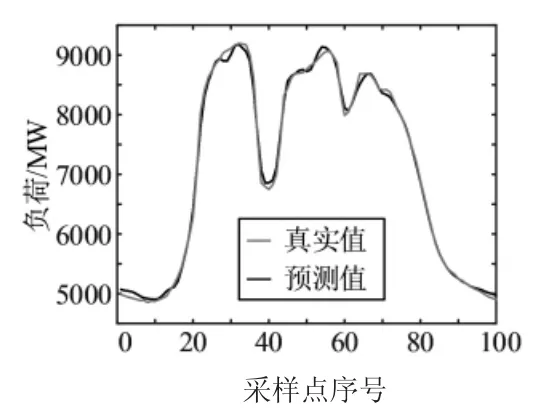
图3 BA-VMD-LSSVM预测结果
进一步计算MAE、RMSE及MAPE等指标,以更加准确地评价预测结果。计算所得评价结果如下:MAE为49.36,RMSE为1.397 5,MAPE为0.73。通过上述指标,可以得知BA-VMD-LSSVM预测模型的精度较高,可以满足工程需要。
4 结语
本文提出一种基于BA-VMD-LSSVM的超短期负荷预测模型。使用VMD分解电力负荷,有效降低了波动性和随机性,增加了负荷的可预测性。与SVM相比,应用LSSVM进行后续预测,可有效减少预测时间,并提高预测精度。通过BA对VMD和LSSVM的参数进行全局优化,以发挥其最佳性能,实现了负荷数据的高精度预测。

