基于模式匹配与深度学习的国际油价预测研究

余乐安,雷凯宇

(1.四川大学 商学院,四川 成都 610065; 2.北京化工大学 经济管理学院,北京 100029)

一、引言

原油在工业社会发展中起着不可替代的作用,故其价格预测一直是学术界研究的热点问题。对于企业和国家做长期规划而言,可靠的多期预测比单期预测更具有实际意义,故本文拟构建模型以重点提升油价的多期预测精度。既往文献曾使用计量经济、人工智能(AI)、混合模型和相似模式匹配模型对油价预测进行探索。对于计量模型,Baumeister等[1]使用向量自回归模型(VAR)预测了原油价格,结果表明VAR模型比AR与ARMA模型具有更高的方向精度;Zhao等[2]使用自回归移动平均(ARIMA)模型来预测国际原油价格,发现这一模型在短期预测上具有显著优势。对于AI模型,Xie等[3]提出了一种基于支持向量机(SVM)的原油价格预测新方法,取得了较好的预测精度;Tang等[4]使用随机向量函数链路(RVFL)预测WTI油价,结果表明没有迭代过程的RVFL计算时间短且能达到较高的预测精度;Yu等[5]利用极限学习机(ELM)和扩展极限学习机(EELM)对WTI原油价格进行了预测,也得到了较高的预测精度。不同于单个模型,混合模型可以克服单个模型的缺点,Wang等[6]将人工神经网络(ANN)和基于规则的专家系统(RES)以及文本挖掘(WTM)技术相互集成,开发了一种新颖的混合模型用于油价预测;Zhang等[7]提出了一种EEMD-PSO-LSSVM-GARCH的混合方法用于原油价格预测,并证明了该方法对原油价格具有很强的预测能力。相似模式匹配模型是一类能够一次输出未来多个预测结果的模型,在多期预测任务上表现良好,Singh等[8]第一次在金融序列长记忆性的基础上提出了PMR方法,并可以一次输出多期预测结果;Fan等[9]也在此基础上构建了GPM模型,使用遗传算法对相似模式匹配过程进行寻优,取得了多期预测精度的提升。综上,受到模式匹配思想与深度学习训练过程可以互相嵌入的启发,本文拟将二者结合进行模型构建,且通过多种相似性度量方法的综合增强模型鲁棒性,提升国际油价多期预测精度。

二、模型方法

(一)总体框架

为了充分挖掘隐藏在油价历史数据中的有用信息,同时能够利用AI方法强大的非线性拟合能力[10],本文提出了一种基于模式匹配与深度学习的原油价格预测模型。该模型由2个主要步骤组成:第一步为形状相似性判断,这一步拟基于相似模式搜寻的思想进行建模;第二步为相似模式驱动的参数训练,按照第一步选出的相似模式进行模型参数训练,采用对特定时间段加权的方式来使模型更加关注特定形状的学习。所提方法的整体框架如图1所示。

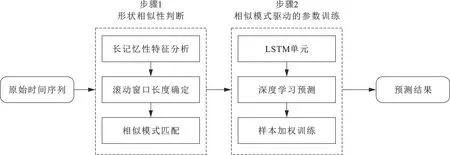
图1 基于相似模式与深度学习的算法流程

从图1中可以看出,模型中的2个步骤总共包含4个核心环节,下面分别对这4个环节进行详细介绍。

1.滚动窗口长度确定

原油价格的记忆性特征是指当前油价走势与历史上某些时间段具有很强的相关性[11],需要依据记忆性特征来确定滚动窗口的长度。英国水文学家Hurst[12]提出的R/S分析法常被用来对序列的记忆性进行度量,由于改变R/S分析法的窗口长度可以影响生成R/S序列的标准差、极差、子间隔个数等因素,从而对最终的Hurst指数产生影响,这也说明在不同窗口长度下序列会表现出不同的记忆性强度。故本环节先使用R/S分析法对原油价格的长记忆性特征进行检验,并通过改变R/S分析的参数值判定原油价格的最优记忆性尺度,然后基于记忆性强弱确定最优滚动窗口长度(即相似模式长度)。

2.相似模式匹配

首先将实验数据划分为训练集与测试集,并以训练集的最后一个窗口作为油价变动的当前模式,然后,按照与当前油价波动状态的“相似性”进行模式匹配与寻找。[13]为了增强整体模型的鲁棒性,采用长度标准化的欧氏距离[14]、相关系数[13]、均方误差[13]3种不同的相似性度量方式,并为每一种方法设定一个阈值,历史序列中相似性指标大于/小于此阈值的即被选为当前模式的相似模式。最后,本文还将3种方法所选出的相似模式区段取交集,以获得更为鲁棒的相似模式,方便后续产生更为鲁棒的预测结果。

3.样本加权训练

根据找出的当前模式的历史相似模式对训练样本进行加权,这一步骤的基本原则为根据历史中所有模式与当前模式的相似性进行加权:当历史模式与当前模式之间的相似性高时,它在训练过程中就被赋予更高的权重,以体现训练过程对于相似模式的关注。最终训练出带有权重因素的深度学习模型,然后对测试集进行预测。

4.深度学习预测

在预测环节,本文选用长短期记忆网络(LSTM)这一深度学习模型进行向前预测,这一网络结构包含一系列循环连接的子网络,每个记忆模块包含一个或多个自连接的细胞以及控制信息流动的输入门、输出门和遗忘门三个门限单元系统,故其能够很好地处理时间序列数据前后之间的依赖关系。[15]

(二)滚动窗口长度确定——R/S分析

将实证数据划分为训练集和测试集之后,需要选定训练集的最后一段作为当前油价模式,而当前模式的长度确定是一个十分重要的问题,这一长度的选取将直接影响最终相似模式寻找的质量。时间序列的长记忆性现象表明序列会在当前与历史上的某些窗口具有一定相似性[16-17],故在进行模式匹配之前,应该基于时间序列的长记忆性特征进行滚动窗口长度的选择。使用R/S分析法对油价序列的记忆性进行度量,其基本原理是通过更改时序数据的时间尺度分析其统计特性的变化,其具体步骤如下。

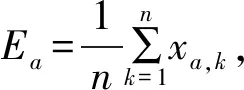
(2)计算每个子间隔的累积离散度。

(1)

(3)基于式(2)计算每个子集合的极差。

Ra=max (Xa,k)-min (Xa,k)

(2)

(4)使用标准偏差和极差来计算每个子间隔的重标度极差,即Ra/Sa。m个子集合的平均重标度极差可以表示为

(3)

(5)改变时间窗口n后,重复上述步骤计算以得到长度为n的所有子集合的(R/S)n。当n为无穷大时,存在E(R/S)n=cnH,对数处理后有lnE(R/S)n=lnc+Hlnn,其中,Hurst指数(H)是该式的斜率,c为常数。

Hurst指数是衡量时间序列记忆性强弱的重要指标,最优的Hurst指数可以保证这个窗口是容易被“记忆”的,即以这个窗口为一个记忆周期的可能性较大。故本文通过修改起始窗口长度这一参数以获取不同的Hurst指数,最终选取最大的Hurst指数所对应的窗口长度作为模式长度,以这一窗口长度进行窗口划分可以获得最强的记忆性强度,故以这一窗口长度作为记忆周期较为合理。

(三)相似模式匹配

相似模式匹配即根据模式之间的相似性对模式进行分类的过程[9],在不同文献中,相似性度量的方法各不相同。根据当前模式和滚动窗口操作得到的多个历史模式,按照历史模式与当前模式之间的相似性程度进行相似模式匹配,并采用对特定时间段加权的方式来使模型更加关注特定形状的学习。这里选择长度标准化的欧式距离、皮尔逊相关系数以及均方误差作为模式之间的相似性度量方法,这3类方法都是时间序列相似性度量的常用方法。而为了保证找出相似模式的鲁棒性,本文将3种方法找出的相似区段取交集处理,因为这些区段通过这3种度量方式都可以取到,故认为它们是带有鲁棒性的相似区段。

欧式距离是最常用的距离度量方式,在这里使用长度标准化的欧氏距离来进行距离度量,消除序列长度对相似性度量的影响,从而更关注形状对于相似性的影响,其公式为

(4)

式中:TX,TY为两条时间序列;n为它们的长度;i为序列的第i个点。

皮尔逊相关系数通常用于衡量两个序列之间的相关程度,在本文中指的是两个序列之间的相似性,其值介于-1与1之间,其绝对值越大表明两条序列之间的相似性越大[13],其公式为

Pearson(TX,TY)=

(5)

均方误差(MSE)也常用来度量两个序列之间的差异性大小[13],是衡量“平均误差”的一种较方便的方法,均方误差越小,说明两个序列之间的差异越小、越相似,其公式为

(6)

为了找出历史中与当前模式形状相似的模式,需要为每一种度量方法设定一个阈值,当历史模式的度量值大于/小于这一阈值时即被认定为相似模式。对于距离指标(欧式距离与均方误差),本文参考Zakaria等人的方法来确定阈值[14]。而对于相关系数指标,现有文献没有统一的标准,故最后对这一参数的取值敏感性进行分析。

(四)样本加权训练

利用上一步选择出的相似模式,本步骤对训练样本进行加权。加权的方法为:与当前模式相似性高的窗口(相似模式)被赋予高权重,与当前模式相似性低的窗口被赋予低权重,而对样本进行加权则通过影响机器学习模型训练中的误差传播与损失下降过程实现。为了增强模式匹配过程的鲁棒性,分别对皮尔逊相关系数、欧式距离与均方误差3个指标进行赋权方法的定义。

对于相关系数的指标,历史模式与当前模式之间的相关系数越高,它在训练中的样本权重就越高,其公式为

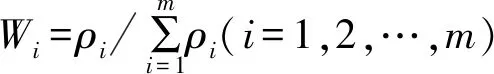
(7)

式中:ρi为第i个模式与当前模式之间的相关系数;m代表所有历史模式的个数。

对于距离指标(欧氏距离与均方误差),历史模式与当前模式之间的距离越近,其被赋予的权重应该越高,反之应该越低。以欧氏距离为例,这里采用常用的反函数加权法进行赋权,为了避免分母为零,一般在赋权时需要在分母上加上均值,具体公式为

Wi=1/[dist(pi,cs)+mean(dist(pi,cs))]

(8)

式中:pi为第i个模式;cs为当前模式;dist可以为欧式距离,也可以为MSE距离。

(五)深度学习预测

由于本文是时间序列预测场景,故采用长短期记忆网络(LSTM)模型[15]作为油价预测的主体模型,并通过修改模型内部结构,完成回归预测和方向预测两种任务。对于水平预测,模型接受带有相似模式加权的价格序列样本作为输入,并通过误差反向传播训练出带有相似模式权重因素的网络,完成向前预测。而对于方向预测,本文拟搭建二分类网络,预测向前2、4、8期的油价比今天是涨(1)还是跌(0),故模型接受带有权重因素的历史涨跌(0/1)序列作为输入,并将涨跌信息(0/1)作为预测结果,最后用精度(Accuracy)指标代替方向精度。

样本权重对模型训练的影响会通过损失的下降过程来实现,算法在进行反向传播时会把每个样本的训练损失乘以其对应权重,故之前被赋予特定权重的相似区段样本则会在训练中带来更大的损失下降,最终影响整体模型的训练效果,使模型更关注相似区段样本所包含的信息。在之后的实证中也会对相似模式加权影响训练损失这一现象进行验证。

在网络结构方面,为了使实验具有可比性,回归预测和方向预测模型主体部分都是使用LSTM单元,但在回归网络中,使用重复向量(Repeat Vector)层和时间分布(Time Distribution)层联合产生序列多期预测的结果,而在分类网络中则分别将它们替换为随机失活(Dropout)层和普通的全连接层(Dense),并且在最终的输出层中将线性激活函数替换为S型激活函数(Sigmoid)。

三、实证分析

自2005年以来,国际原油价格受多方面因素影响而呈现出剧烈波动,故为了验证所提方法的有效性,选择Brent原油期货价格2005年1月1日到2022年2月26日共896个周度数据进行实证分析。

(一)实验设计

按照8∶2的比例,将实验数据划分为训练集与测试集,并选择训练集的最后一个窗口作为当前模式。使用训练集训练模型,并在测试集上验证效果。为了将基于模式相似性的方法和深度学习方法融合起来,预测模型的主体使用LSTM模型,并利用找出相似模式对训练数据进行加权训练,最终用带有样本权重的LSTM模型对Brent油价进行向前预测。

在进行模式匹配之前,首先需要确定模式长度。本文使用R/S分析法,通过改变最短时间间隔这一参数得出不同起始时间间隔下的Hurst指数,然后选择Hurst指数最大的时间间隔作为窗口长度。在确定窗口长度之后,对训练集数据进行滚动窗口操作,得到多个长度相等的滚动窗口(子序列),选择最后一个滚动窗口作为当前模式。

接下来分别使用相关系数法、长度归一化的欧式距离与均方误差距离来寻找相似模式,为了解决不同时间段油价尺度不一样的问题,统一将训练集所有滚动窗口进行归一化,这样便可得到尺度在(0, 1)之内、消除尺度影响而只体现具体形状差异的多个模式。

在找出相似模式之后,根据各个模式与当前模式之间的相似性对训练数据进行加权并输入模型,训练出带有权重因素的预测器,然后对测试集分别进行向前2周、4周和8周的多期预测。将所提模型(3种不同的加权方式)与常见的深度学习模型LSTM、多层感知机(MLP)以及机器学习模型支持向量回归(SVR)、决策树(DT)、岭回归(Ridge)和计量模型自回归移动平均(ARIMA)、指数平滑(ES)作对比,以验证相似模式加权的有效性以及基于模式的预测方法的有效性。

为了比较不同模型的性能,选择水平精度和方向精度作为评价标准。具体而言,平均绝对百分比误差(MAPE)和均方根误差(RMSE)被用来衡量预测结果的水平精度[18-19],其指标的具体计算方法如式(9)和(10)所示。

(9)

(10)

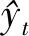
而对于方向精度,将油价所在时间区间内的油价涨跌情况进行统计,发现在实验期内油价的涨(1)跌(0)情况接近1:1的比例,所以在分类实验中不需要考虑类别标签不均衡[20]的问题,这也进一步说明了使用分类精度(Accuracy)指标直接衡量方向精度的合理性。

最后,为了在统计学意义上证明所提方法的优越性,本文分别对不同模型的预测结果进行DM检验(Diebold-Mariano Test)[21-22]。

(二)实验结果分析

1.长记忆性特征分析

使用经典的R/S分析法对Brent原油价格序列的长记忆性特征进行检验,并通过改变R/S检验中的时间间隔参数来得到不同的Hurst指数。通过调节最小窗口长度计算出不同的Hurst指数来确定油价的记忆周期[23]。根据图2结果可知,窗口的长度确定为19(周)较好,因为这时的Hurst指数最大,即以这个窗口为一个周期的记忆性较强。同时,当Hurst指数大于0.5时,时间序列数据具有长期记忆性特征[24],且Hrust指数的值越大表明数据的记忆性越强[25],油价序列的Hurst指数最大约为0.72,故这一时间序列具有正向的长期记忆性特征,即历史序列波动会与当前序列波动形状相似,适合于使用基于模式相似性的方法和尺度变换进行预测分析。

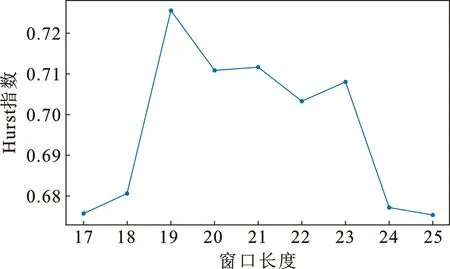
图2 不同窗口长度下Brent油价序列的R/S分析结果

在确定窗口长度为19之后,对长度为717(896×0.8)的训练集数据进行滚动窗口操作,共获得717-19+1=699个滚动窗口,每一个滚动窗口都是一个模式。选择训练集最后一个滚动窗口为当前模式,其他训练集数据为历史模式,并从中寻找当前模式的历史相似模式。

2.相似模式匹配

接下来,根据历史模式与当前模式之间的相似性进行相似模式匹配。为了增强鲁棒性,本文选择长度标准化欧氏距离、相关系数、均方误差总共3种相似性度量方式进行匹配,将每一种方式的匹配结果用于测试集的预测,并进行精度效果对比。

将序列尺度归一化后,首先使用相关系数法寻找相似模式,相关系数大于阈值的历史模式即被选为相似模式,不同阈值下的结果如表1所示。最终选择相似模式的阈值为0.6,所找出的相似模式如图3所示,虚线型为当前模式,十字花型为找出的所有历史相似模式。然后根据每个历史模式与当前模式之间的相似性对训练样本进行加权,当作之后预测模型的输入。在后面的模型参数讨论部分将对相关系数加权法阈值选择问题进行更具体的实证分析,以验证0.6这一阈值选择的合理性。

表1 不同相关系数阈值下找出的相似模式个数

使用长度标准化的欧式距离和均方误差两个距离指标寻找当前油价模式的历史相似模式,并按照设定的相似性阈值判定方法[14]进行相似模式的搜寻匹配。其匹配结果如图4和图5所示,距离小于既定阈值的时间窗口模式即被判定为当前油价模式的历史相似模式。图4和图5分别展示了利用长度标准化的欧氏距离和均方误差距离找出的相似模式结果(最后的虚线为当前模式),可以看出前者找出了14段相似模式,而后者找出了10段。这也同时说明使用不同的距离度量方式进行相似模式匹配确实会得到不同的结果。

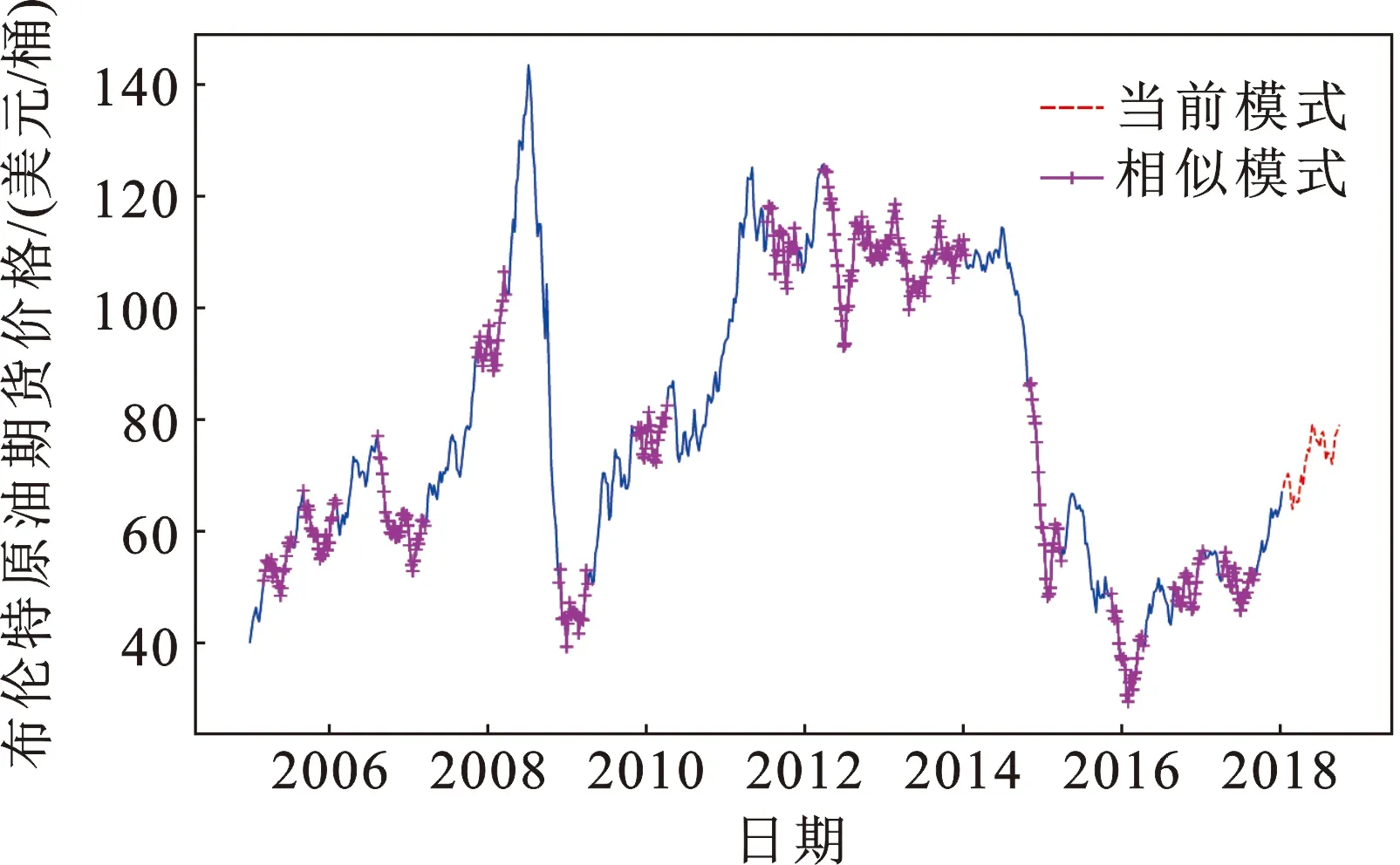
图4 欧式距离选出的相似模式

图5 均方误差距离选出的相似模式

为了增强模式匹配过程的鲁棒性,接下来对3种方法下找出的相似模式取交集,以找出在任何相似性度量方式下都能够找出的相似模式,取交集后发现得出的相似模式同样如图3所示,即与相关系数法找出的相似模式相同,故在后面预测实验中也会重点关注相关系数法找出的相似模型区段加权后(作为鲁棒相似模式)的预测性能,并分别与欧式距离、MSE距离加权的预测结果以及其他基准模型相对比,以验证相关系数法寻找出的鲁棒相似模式在预测性能上的优越性。

接下来利用找出的相似模式对训练样本进行加权,训练出带有样本权重因素的预测器用于后续的预测工作。

3.预测精度分析

将通过3种不同加权方式训练出的模型与上文中提到的多种基准模型相对比,并统一做向前2周、4周和8周的多期预测,各个模型的预测在水平精度上的表现如表2所示。发现在向前2周、4周和8周的预测中,相关系数加权模型的所有水平指标都表现最好。但随着预测步长的增长,在向前8周的预测中,相关系数指标的预测精度与欧式距离、均方误差距离的整体水平精度相近。同时,所提出的3种相似模式加权LSTM模型的表现不仅比未加权的LSTM模型要好,而且比其他基准模型都要好,这不仅说明了本文所提出的“基于相似模式加权”这一技巧的有效性,而且还说明了基于模式相似性这一类预测模型较其他模型的有效性。另外,所提模型中不同相似性度量方式之间的对比说明基于相关系数搜寻的相似模式比其他度量方式所找到的相似模式质量要高,具有更高的预测性能。

表2 预测水平精度对比

进一步地,使用LSTM分类网络来预测油价的涨跌情况,并利用精度(Accuracy)指标评估方向预测的准确性。为了使实验效果易于对比,本步骤中仅选用相关系数加权的模型作为主推模型与其他基准模型进行比较。同时,在对比模型中,剔除岭回归这一回归模型。实验结果如表3所示。

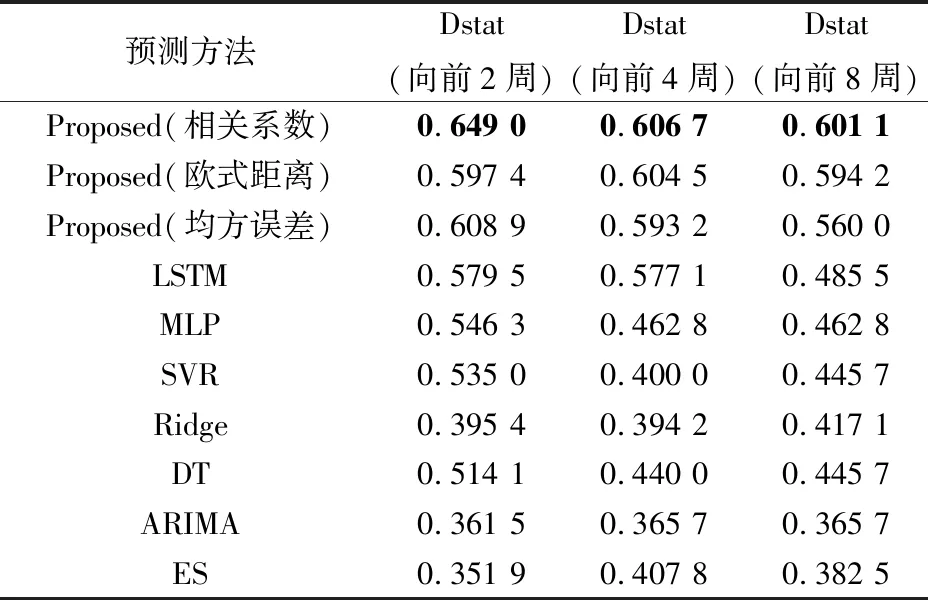
表3 预测方向精度对比

从表3中可以看出,在所有基准模型中,LSTM模型的预测方向精度最高,这是因为其本身适合于时序信息记忆问题。而所提模型在多期预测方向精度上比大部分模型要好,这是由于所提模型的主体也是LSTM模型,只是加了相似模式的样本加权训练的机制,且可以看出所提出的3种模型在向前2、4、和8步预测的方向精度上可以超过基准LSTM模型,这也证明了所提相似模式加权的技巧可以适用于油价方向预测的分类任务。另外,单独对比所提模型发现,基于相关系数加权的方法在方向精度上也优于其他两种度量方法,且与水平精度不同,随着预测步长的增长,相关系数方法在水平精度上的优势越来越明显。这可能是因为相关系数本身在度量相似性的时候会关注到序列之间形状上的相似性,故在进行加权训练时使模型学习到了形状走向的变化规律。而距离度量方式只是单纯地将与当前模式距离较小的模式找了出来,并没有考虑形状因素,故其在方向精度,尤其是多步多期方向精度上的表现不如相关系数法。

最后,为了验证所提模型相较其他模型在统计学意义上的优越性,对预测结果进行DM检验。由于之前的实验证明了基于相关系数加权模型的优越性,故为了凸显模型性能,此处只选择相关系数加权的所提模型进行检验。DM检验的结果如表4所示。

通过表4可以看出,在向前2周的预测中,除了ARIMA模型,其他所提出模型的预测效果在统计学意义上比所有基准模型都要好,第一行DM值都为负,且p值都小于0.1,在90%的置信度下可以相信模型效果比大部分基准模型要好;在向前4周的预测中,所提模型的预测效果在统计学意义上显著优于其他所有模型;在向前8周的预测中,所提出模型的预测效果在统计学上意义上优于所有模型。由DM检验的结果可知,所提模型在各个步长任务上的预测结果均具有一定优势,且这种优势随着预测步长的增加而变得更明显。

(三)模型参数讨论

虽然相关系数加权的模型在各项性能上表现优越,但其阈值的选择也是一个主要问题,因此,应对相关系数加权法确定相似模式的阈值进行讨论。与“距离”方式的加权不同文献给出的阈值的公式有所不同,相关系数加权需要对特定的阈值所找出的相似模式以及每一种阈值取值情况下的模型预测效果进行具体的灵敏度分析。相关系数阈值在不同时的模型预测效果对比如表5所示。

表5 不同相关系数阈值的预测效果

结合表1不同阈值下找出的不同相似模式段数可以看出,在向前2、4、8周预测的任务中,相关系数阈值为0.6时均取得了最好的效果,而在训练过程中,虽然相关系数为0.5时选出的相似模式较多(15段),但其在预测实验中的表现却不如阈值为0.6时的结果。这说明加权训练的模式越多不一定训练过程越彻底,最后的精度也不一定越高,还要看模型在加权训练中是否学习到信息,也就是说,虽然阈值为0.5时找出的相似模式较多,但并不是每一个模式的加权训练都带来了训练损失的大幅度下降。因此相关系数方法确定相似模式的阈值为0.6是合理的。

四、结语

(1)不同的滚动窗口长度会影响油价序列的记忆性强度,通过记忆性检验发现,当窗口长度设定为19周时,Brent油价序列的Hurst指数可以达到最大,故以19周作为一个记忆周期可以获得较强的记忆性效果。

(2)所提出的加权模型不仅比一般机器学习(深度学习)的模型要好,而且比未加权的模型要好,且进一步用DM检验验证了这一点。这说明所提出的基于相似模式加权训练的技巧确实可以提升模型在预测中的性能。而使用所提模型分类方法对油价变化的方向做出预测取得了较好的方向精度,这说明相似模式加权的技巧对油价方向预测(分类任务)同样也有较好效果。

(3)对不同相似性度量方式找出的相似模式取交集,发现基于相关系数找出的相似模式更为鲁棒,且其预测能力比欧式距离和MSE距离找出的更强。

(4)通过对相关系数阈值设定的讨论可以看出,所找出的相似模式的个数确实能影响训练过程与最终的模型效果,但并不是加权相似模式越多精度越高,具体还要看每一段模式中加权是否能带来信息。