基于DMD降噪的滚动轴承故障诊断方法
涂福泉,杨家瑜,陈 超,罗迎九,吴维崧
(武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081)
滚动轴承是机械传动中的重要组成部件,广泛应用于各种机械设备,如风电机组、高速列车、航空发动机等。由于工作环境的复杂性,滚动轴承容易出现点蚀、断裂、磨损等故障,从而影响设备运行的稳定性和可靠性,因此对滚动轴承进行故障诊断具有重要意义。
在设备故障诊断时,通常是利用传感器收集的振动信号进行分析。这些振动信号中有大量的噪声,导致其故障特征不明显,难以直接应用,需要将原始信号进行降噪处理,再进行下一步的分析[1]。经典的信号降噪和特征提取方法包括小波变换(WT)、经验模态分解(EMD)、变分模态分解(VMD)、奇异值分解(SVD)等,然而这些方法都有一些不足之处。例如,WT需要选择合适的母小波及分解层数;EMD公式缺乏严格的理论推导,并且存在模态混叠和端点效应等问题;VMD的参数选择对其分解效果影响较大;SVD对强噪声背景下的信号特征提取效果欠佳。因此,研究人员以上述方法为基础提出了一系列的改进措施。Yang等[2]针对传统的采用单一准则优化的小波参数无法完全描述故障特征的问题,设计了一种多目标优化小波滤波器用于提取轴承故障特征,在强噪声背景下的应用效果较好。滚动轴承早期故障信号存在大量噪声使得故障特征提取十分困难,为此曹玲玲等[3]提出一种将互补集合经验模态分解(CEEMD)和改进小波阈值算法相结合的方法,可以提高故障信号的信噪比,降噪效果明显。Yin等[4]提出一种滚动轴承弱故障特征提取方法,能选择出具有故障特征的内模函数,并且通过新构造的自适应阈值进行信号去噪。赵玮[5]采用基于VMD和奇异值差分谱的故障特征提取方法,可以有效降低噪声的影响。鉴于传统VMD方法对高速列车轮对轴承故障特征提取不够准确,李翠省等[6]设计一种结合集成经验模态分解(EEMD)和改进参数自适应VMD的方法,其在强噪声干扰下仍具有优良的故障特征提取效果。李华等[7]为了提升SVD方法的降噪性能,提出一种基于相关奇异值比的SVD方法并成功应用于轴承故障诊断。Cheng等[8]提出自适应周期模态分解方法,以解决现有滚动轴承故障诊断方法对周期性冲击故障识别能力差的问题。
动力学模态分解(dynamic mode decomposition,DMD)是基于Koopman算子的无方程数据驱动分析方法,它不仅有SVD算法的优点,还考虑了机械系统演化过程中的时空特性,具有时空耦合建模的独特优势,在信号降噪和特征提取方面已得到有效应用[9]。DMD本质上是一种融合奇异值分解和模态分解理论的空间降维方法,因此它也不可避免地继承了两者的缺点,例如在截断秩的选取和含调制成分信号的处理方面存在困难。针对上述问题,本文提出一种Hilbert变换和DMD相结合并通过奇异值差分谱确定截断秩的信号降噪和特征提取方法,用于滚动轴承故障诊断。首先使用Hilbert变换对原始信号进行包络解调,消除原信号中调制成分对后续分析的影响,然后进行动力学模态分解,通过奇异值差分谱选择合适的截断秩进行信号重构,从而减少噪声的干扰,以达到较好的特征提取效果。本文最后利用仿真信号和美国凯斯西储大学公开的轴承故障数据集进行方法验证。
1 基本理论
1.1 Hilbert变换
对一个连续信号x(t)进行Hilbert变换可表示为[10]
(1)
式中:H[x(t)]表示时域中的Hilbert变换,⊗为卷积算子。
原信号的解析信号为
(2)
从解析信号中可以得到原信号x(t)的包络信号为
(3)
1.2 DMD算法
假设两个连续序列X、X′(用矩阵形式表示)满足与最优线性算子的映射关系,即X′=AX,DMD算法利用矩阵A的低秩表达式来捕捉连续序列潜在的动态特性[11-12]。
由于DMD最初是应用于流体力学领域,所收集的信号通常是二维矩阵形式,而轴承振动信号是一维的,因此需要将一维振动信号转换为矩阵形式,这里构造Hankel矩阵以满足上述要求[13]。对于振动信号X(t)=[x(1),x(2),x(3),…,x(N)],其Hankel矩阵形式为
(4)
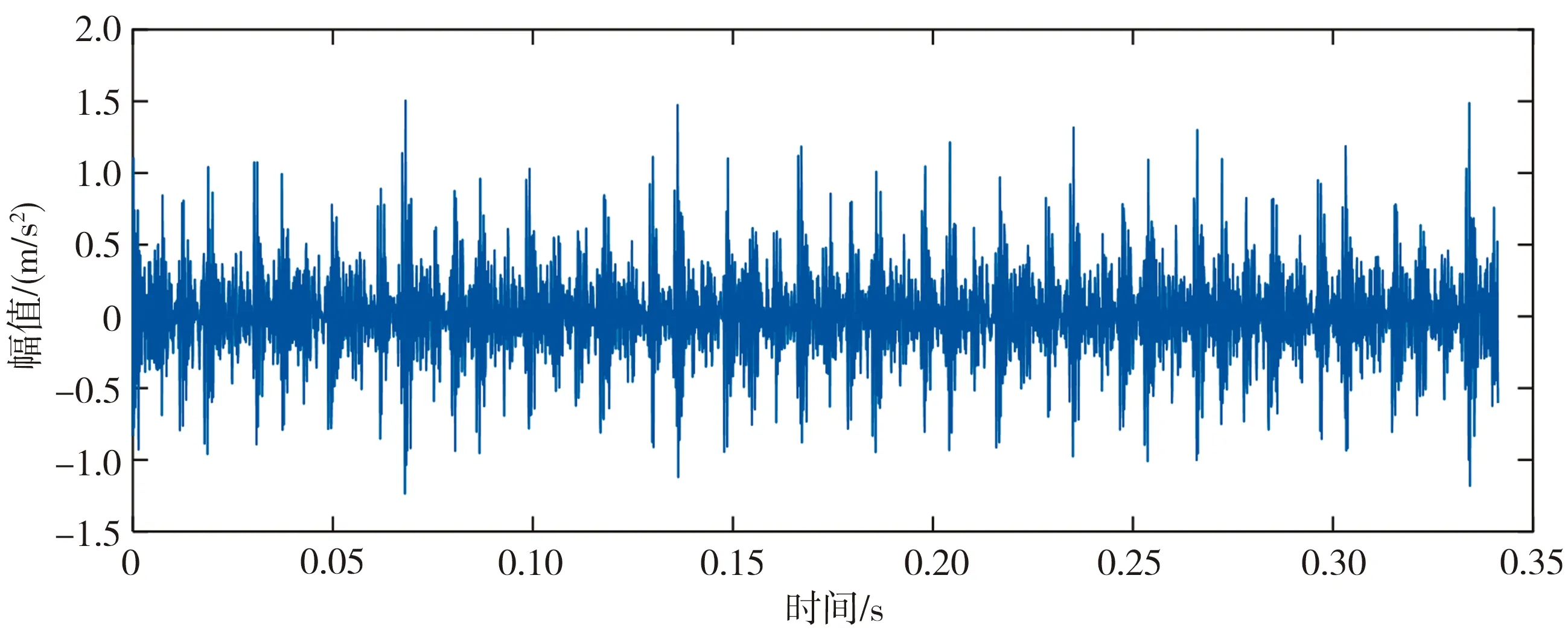
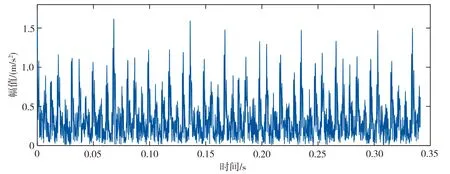
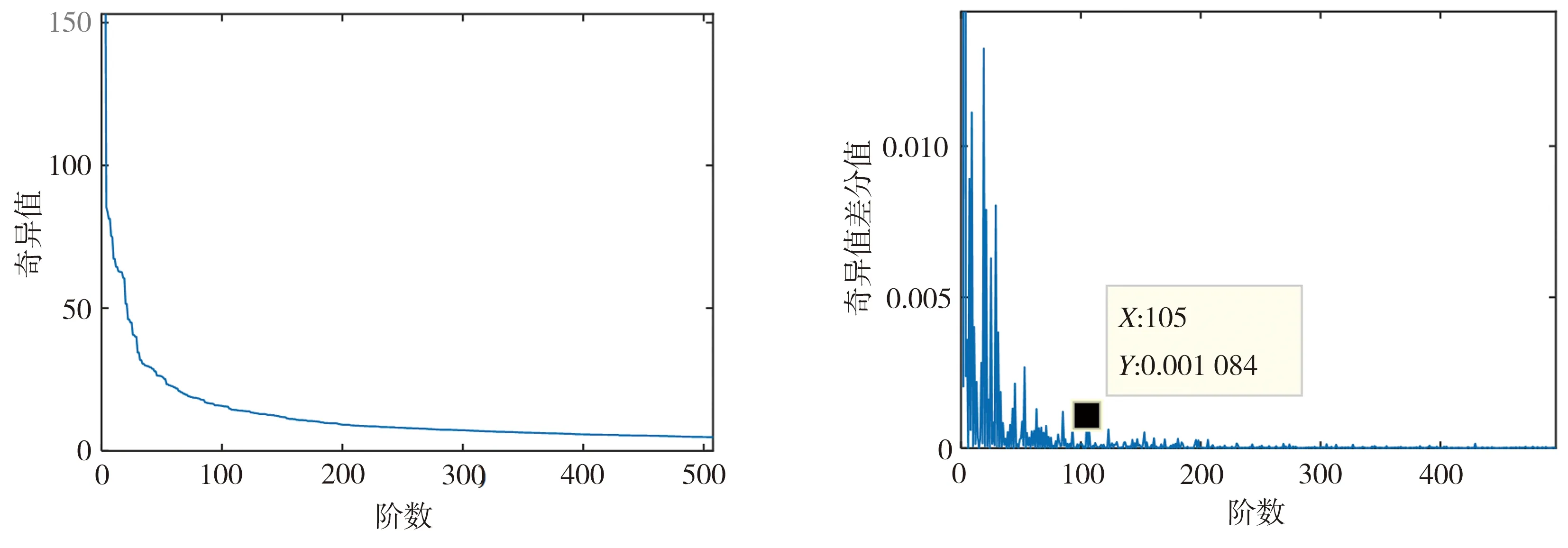
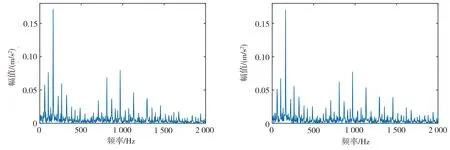
式中:m=N/2,1 DMD算法步骤为: 1)对X进行奇异值分解 X=UΣV* (5) 式中:U、V为酉矩阵,Σ为奇异值对角矩阵。U的每个列向量相互正交,是X的本征正交分解(POD)模态。取U的前r阶来截断数据,通过保留主要模态来降维。 2)利用X的伪逆来求A A=X′XT=X′VΣ-1U* (6) (7) (8) 4)计算重构矩阵 (9) (10) 式中:wi=ln(λi)/Δt,bi是每个模态的幅值。 奇异值差分谱可以表征奇异值序列的变化,差分谱计算公式如下[14]: (11) 式中:σi为奇异值。所有的di构成奇异值差分谱,差分谱的峰值与信号特征相关,峰值越大,特征越明显,当峰值降低到一定程度便可截断。 本文方法的基本流程如图1所示。首先将原始信号进行Hilbert变换得到包络信号,再根据包络信号构造Hankel矩阵进行动力学模态分解,然后通过奇异值差分谱确定DMD的截断秩,使用该截断秩进行重构得到重构矩阵,其第一行为重构信号,根据重构信号进行频谱分析,提取出准确的信号特征,从而实现滚动轴承故障的精确诊断。 图1 本文方法的基本流程 下面采用滚动轴承内圈故障仿真信号来验证本文方法的有效性。仿真信号表达式如下[15]: (12) 式中:fr为转频,fn为轴承的共振频率,T为故障周期,C为衰减系数,A0为幅值,n(t)为高斯白噪声。 设定采样点数N=4 096,高斯白噪声的信噪比为-5 dB,仿真信号其余参数的具体取值如表1所示,其中fs为系统的采样频率。 表1 滚动轴承内圈故障仿真信号的参数 图2为仿真信号的时域波形图。由图2(b)可见,时域信号的故障特征已经被噪声淹没,从中无法获得轴承故障频率。为了分析信号的故障特征,对加噪声后的仿真信号进行包络谱分析,结果如图3所示。在图3中可以找到信号的特征频率和部分多倍频,但是包含大量的噪声信息。 (a)未加噪声的仿真信号 图3 加噪声仿真信号的包络谱 为了更加有效地提取轴承的故障特征,使用本文方法进行信号分析。首先将原始信号通过Hilbert变换构造解析信号,对解析信号取模得到包络信号,如图4所示。 图4 本文方法得到的包络信号 根据包络信号构造Hankel矩阵,进行动力学模态分解,通过奇异值差分谱确定截断秩的阶数,如图5所示。需要在奇异值分布曲线上选取一个合适的截断秩阶数,但是仅根据图5(a)难以确定最优点,因此可以根据奇异值差分谱进行分析。在理想状态下,差分谱峰值的大小与信号特征相关,峰值越大,特征越明显,当差分谱峰值降低到一定程度而难以区分特征信息时便可截断。如图5(b)所示,通过奇异值差分谱分析,设定奇异值差分阈值为0.001,取最后一个峰值大于阈值的差分阶数作为截断秩阶数,最终确定的截断秩阶数为31。 (a)奇异值分布曲线 (b)奇异值差分谱 根据设定的截断秩阶数,可以得到31个精确DMD模态,然后构造DMD重构矩阵,选取其中第一行为重构信号。通过DMD重构后的信号如图6(a)所示,从中可以观察到故障特征。利用快速傅里叶变换(FFT)对重构信号进行频谱分析,结果如图6(b)所示,可以观察到特征频率及其多倍频,谱线突出,特征频率附近存在一对边频,4倍频附近存在一个上边频。上述结果表明,本文方法能有效降低轴承振动信号中的噪声干扰,可提取出轴承故障特征频率。 图7所示为对比方法(包括SVD、自适应DMD、VMD、EEMD)对仿真信号的分析结果。SVD重构信号的包络谱中特征频率和部分多倍频谱线明显,但是存在部分噪声;自适应DMD重构信号的包络谱中特征频率和部分多倍频谱线突出,但高于5倍频的特征不明显,部分特征信息丢失;选取VMD重构信号中合适的模态分量(IMF3)进行分析,其包络谱中故障频率、2倍频和3倍频的谱线较明显,但伴随有部分噪声;选取EEMD重构信号中合适的模态分量(IMF1)进行分析,其包络谱中故障频率、部分多倍频的谱线较明显,但噪声较多。 (a)SVD重构信号的包络谱 (b)自适应DMD重构信号的包络谱 为了进一步验证本文方法在实际应用中的有效性,以美国凯斯西储大学公开的轴承故障数据集中的内圈故障数据为案例进行分析。轴承故障直径为0.007英寸(0.01778 cm),转速为1797 r/min,采样频率为12 kHz。通过理论计算,轴承内圈故障特征频率为162.19 Hz。 由轴承内圈故障信号的时域波形(图8)可知,故障特征被噪声淹没,无法提取出有效的特征信息。该信号的包络谱分析结果见图9,从包络谱中可以提取轴承故障特征,但是还存在噪声干扰。 图8 轴承内圈故障信号的时域波形图 图9 轴承内圈故障信号的包络谱 为了更好地提取故障特征信息,使用本文方法对原始信号进行降噪处理。首先将原始信号通过Hilbert变换得到包络信号,如图10所示。根据包络信号构造Hankel矩阵后进行动力学模态分解,并通过奇异值差分谱确定截断秩的阶数。轴承内圈故障信号的奇异值分布及奇异值差分谱如图11所示,据此选取合适的截断秩阶数。从图11(a)来看,应选取曲线变化趋于稳定的一个点。设定奇异值差分阈值为0.001,结合图11(b),确定截断秩阶数为105。 图10 轴承内圈故障包络信号的时域波形图 (a)奇异值分布曲线 (b)奇异值差分谱 截断秩为105时的DMD重构信号如图12(a)所示,通过FFT得到的频率谱如图12(b)所示。将图12与图8~图9对比可知,尽管从原始信号的包络谱中可以找到特征频率和部分多倍频,但其中伴随着大量的噪声,而经过Hilbert变换和DMD处理后,重构信号的频率谱中噪声明显减少,比较容易找到特征频率和多倍频。由此可见,采用本文提出的将Hilbert变换与DMD相结合、再通过奇异值差分谱确定截断秩的方法可有效降低振动信号噪声,便于提取轴承故障特征。 另外,在采用i5-8300H处理器、16 GB内存、GTX 1050 Ti显卡的实验配置下,本文方法对上述轴承内圈故障信号的计算时间为9.66312 s,计算时间较短。因此,当设备性能较好、采样点数量较少时可通过该方法进行轴承故障信号实时分析。 图13所示为对比方法对轴承内圈故障信号的分析结果。从SVD重构信号的包络谱中可以分辨出故障频率和部分多倍频,但是包络谱中噪声较多;从自适应DMD重构信号的包络谱中可以看出部分多倍频的谱线较为突出,但是噪声干扰较大,部分倍频被噪声淹没;选取VMD重构信号合适的模态分量(IMF3)进行分析,从包络谱中只能观察到特征频率和2倍频,并伴随有噪声影响;对EEMD重构信号的IMF1分量进行分析,其包络谱中故障频率比较明显,可以观察到部分多倍频,但是噪声也较多。相对而言,VMD和EEMD重构信号中特征丢失和噪声剔除不理想的情况更严重。 (a)SVD重构信号的包络谱 (b)自适应DMD重构信号的包络谱 从计算效率角度分析,在实验配置不变的条件下,SVD方法的计算时间为28.53648 s,计算时间较长;自适应DMD方法的计算时间为11.63338 s,计算时间稍长。与SVD和自适应DMD相比,本文方法计算速度更快、降噪性能更优秀。 针对轴承故障诊断中提取故障特征时难以剔除信号噪声的问题,本文提出了一种将Hilbert变换、DMD和奇异值差分谱相结合的方法。首先对原始信号进行Hilbert变换求得包络信号,以分离出原信号中的调幅和载波信息,去除原信号中高频调制部分对后续分析的影响。根据包络信号构造Hankel矩阵,再对该矩阵进行DMD处理。鉴于DMD算法的截断秩选取较为困难,本文通过奇异值差分谱来确定截断秩,当差分值降低到一定程度难以区分特征信息时便可以截断。取DMD重构矩阵的第一行为重构信号,通过FFT得到重构信号的频域谱,从而提取出轴承故障特征。本文方法在对仿真信号和实际的滚动轴承故障信号的分析中均取得了较好的降噪效果,为滚动轴承故障诊断提供了一个有效手段。

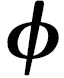
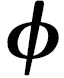
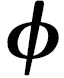

1.3 奇异值差分谱
2 本文方法

3 仿真信号分析






4 实验验证

5 结语

