多孔介质的胞元结构对燃烧温度分布的影响

吴 宏,陈元元,许学成,李本文,胡惊雷

(1.武汉科技大学省部共建耐火材料与冶金国家重点实验室,湖北 武汉,430081;2.武汉钢铁有限公司硅钢部,湖北 武汉,430080)

在众多新型燃烧技术中,多孔介质燃烧技术因具有低排放、高效率、结构紧凑、可燃用低热值燃气等明显优势而备受关注[1],其关键核心在于燃烧器内芯材料的选择。开孔泡沫陶瓷的孔隙率高、比表面积大、换热性能强、流阻低、机械稳定性与耐高温、抗侵蚀性能俱佳,是一种应用较为广泛的多孔介质燃烧器内芯材料[2]。和其它多胞材料类似,胞元是泡沫型多孔介质结构和功能的基本单位[3],众多胞元的交联组合形成了多孔介质的宏观结构,与燃烧有关的多孔介质物性参数如有效导热系数、容积换热系数、辐射衰减系数等均与多孔介质结构有着密切关联。其中,多孔介质孔径对辐射特性影响较大,当孔径增大时,辐射衰减系数减小,辐射穿透距离较远;当孔径减小时,多孔介质光学厚度相应增加,辐射会局限在一个较小的区域内[4-6]。同时,多孔介质的孔隙率和孔径对体系的对流换热系数也有一定程度的影响,孔隙率和平均孔径越大,体系的对流换热系数就越小[7]。此外,孔隙直径与有效导热率还存在反比例关系[8]。

在研究多孔介质的胞元结构对其燃烧性能的影响之前,需进行多孔介质的结构建模。最早见于报道的胞元模型是Gibson等[9]所构建的G-A模型,该模型简化模拟了开孔各向同性的多孔材料结构,并根据初等梁理论计算公式推导出开孔多孔材料的相对密度、骨架厚度及形状等参数与其弹性模量、屈服应力等力学性能参数之间的关系式,相关研究成果至今仍被广泛引用。不过,也有一些研究者认为G-A模型不能真正反映开孔泡沫材料的胞元结构,并提出了八面体模型[10]、十二面体模型[11]等用于相关研究。在不断探索、构建新模型的过程中,Kelvin模型[12]和Weaire-Phelan模型(W-P模型)[13]脱颖而出,被认为是最接近真实泡沫材料结构的胞元模型[14-16]。故而,本文使用Siemens NX软件构建多孔介质胞元结构的Kelvin模型和W-P模型来研究泡沫多孔介质胞元结构参数对温度分布的影响。利用所构建的胞元模型结合拓扑阵列方法,获得有序排列的多孔介质结构。之后,进一步建立两段式多孔介质燃烧模型,并将模型中的关键热物性参数与骨架参数进行关联,在此基础上,借助FLUENT软件对燃烧现象进行模拟,着重分析泡沫陶瓷胞元结构参数对燃烧温度分布的影响。

1 胞元结构建模

利用三维软件Siemens NX构建胞元的Kelvin和W-P几何模型如图1所示。将两种胞元体分别在三维空间中阵列,得到相应有序排列的泡沫多孔介质结构,结果见图2。

(a)Kelvin模型 (b)W-P模型

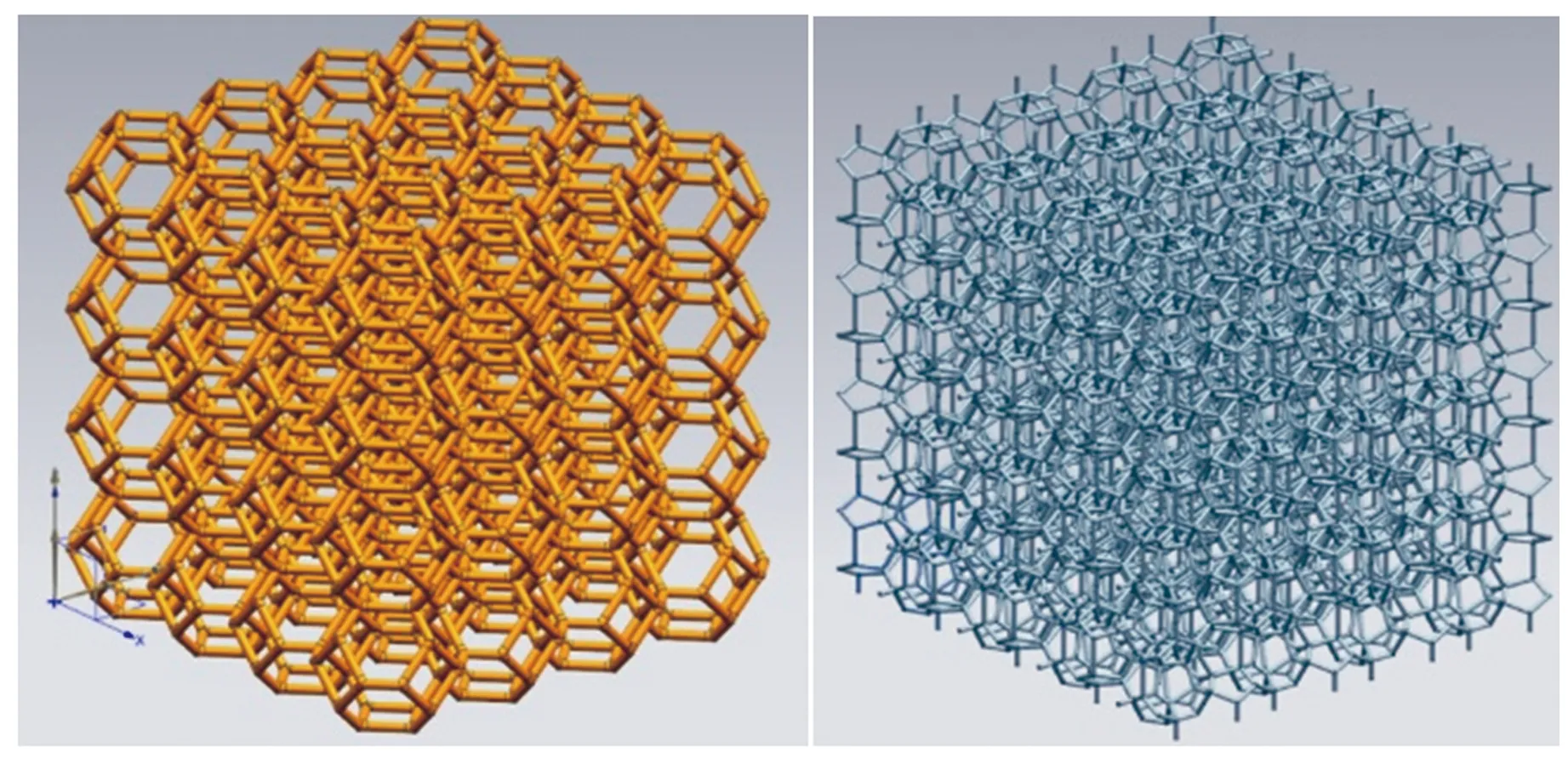
(a)基于Kelvin模型 (b)基于W-P模型

通过改变骨架直径可得到不同的多孔介质结构,利用回归法建立多孔介质孔隙率ε与骨架直径d之间的关系。其中,基于Kelvin模型的关系式为

ε=-0.0151d2-0.001d+1.0002

(1)

基于W-P模型的关系式为

ε=-0.0071d2-0.0007d+1.0001

(2)

2 多孔介质燃烧模型

2.1 物理模型

本文以一种轴对称的圆柱形双层泡沫多孔陶瓷燃烧器为研究对象,其物理模型见图3。该燃烧器全长为6.05 cm,圆柱体直径为7 cm。其中预热区和燃烧区的长度分别为3.5、2.55 cm。预热区材质为部分稳定氧化锆(PSZ),其孔密度即每英寸(25.4 mm)的孔数PPI为65(pores per inch),孔隙率为0.84。燃烧区材质为SiC,其孔密度为10 PPI,孔隙率则根据所用胞元模型以及骨架的直径来确定。

图3 多孔介质燃烧器物理模型

2.2 数学模型

基于图3所示的多孔介质燃烧器物理模型,建立描述其燃烧过程的数学控制方程。根据文献[17]提出假设条件如下:①预混气体为不可压缩理想气体,流动为瞬态层流流动;②多孔介质为灰体均质,各向同性,多孔介质内部固体辐射采用有效导热进行近似,忽略气体辐射;③壁面为无滑移绝热壁面。则有

(1)连续性方程:

(3)

式中,ρg为混合气体的平均密度;u为气相速度矢量。

(2)动量守恒方程:

(4)

式中,p为压力;τ为黏性应力张量;Si为多孔介质渗流阻力项。

(3)组分守恒方程:

(5)

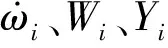
(4)气相能量方程:

·(ελg,effTg)+

(6)

(5)固相能量方程:

Hv(Tg-Ts)

(7)

(6)理想气体状态方程:

(8)

气相进口:ug=ug,in,v=0;YCH4=YCH4,in,YO2=YO2,in;Tg=300 K;

2.3 计算方法

采用商业软件FLUENT对控制方程进行离散求解。通过加载自定义标量(UDS)和自定义函数(UDF)对气/固能量方程、多孔介质物性参数和边界条件进行修正,将单温模型修改为双温模型进行数值模拟,动量方程的求解采用压力-速度耦合的SIMPLE算法,甲烷/空气化学反应则选择一步总包反应机理。在处理化学反应的刚性问题时,为了保证计算的收敛和稳定,采用了亚松弛迭代。在模拟多孔介质点火过程中,将气体温度设置为1800 K。在进行相关计算时,除能量方程的收敛标准为10-6外,其余方程的收敛标准均为10-3。

2.4 网格无关性验证

为了保证计算的可靠性和准确性,需对数值计算的网格无关性进行验证。验证所采用的物性参数表如表1所示,其中的C和m是根据孔径选择的经验参数。验证采用的网格数分别为1344、2100、4116,表2列出了不同网格数下的出口处气、固体温度。由表2可见,当网格数由2100增至4116时,相应出口处气相温度的相对误差仅为0.10%,固相温度的相对误差为0.26%。考虑到计算的准确性并兼顾计算效率,在后续的数值分析中,设定网格数为2100。

表2 不同网格数下的出口处气、固相温度

2.5 有效性验证

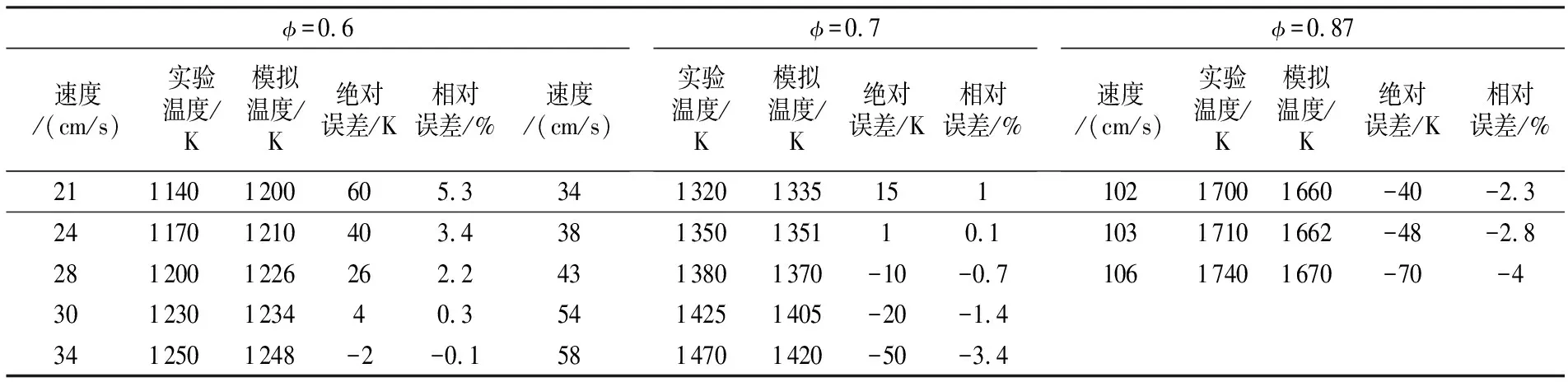
表3 实验对照

3 结果与分析

3.1 入口速度对温度分布的影响

3.2 当量比对温度分布的影响

(a)Kelvin模型

3.3 骨架直径对温度分布的影响

(a)Kelvin模型

由图6(a)可见,对于Kelvin模型,气相的峰值温度在骨架直径d为0.25 mm时最高,但出口气体的最高温度是在骨架直径d为0.35 mm时出现的;当骨架直径d为0.35 mm时,大孔区气体沿轴向的温度梯度最小,气体温度分布最均匀,这得益于固体骨架对温度的弥散作用。同时,出口处固体相的温度也最高。骨架直径越小,气体沿轴向的温度变化量就越大,而固体沿轴向的温度变化量趋势则相反,这表明骨架越细,越有利于提高多孔介质面板的服役寿命。因此,综合考虑多孔介质的辐射效率以及服役寿命,需对骨架直径进行合理设计。由图6(b)可见,对于W-P模型,气、固相温度均随着固体骨架直径的增加而升高,骨架直径越大,气体温度沿轴向的变化梯度就越小,而固体温度沿轴向的变化梯度就越大,出口处气体温度和固体温度的最高值均出现在骨架直径d为0.35 mm时,这表明骨架直径越粗,越有利于提高多孔介质面板的辐射效率。对比两种模型可以看出,在同样工况下,W-P模型固相温度分布较Kelvin模型更均匀,表明W-P模型具有更长的服役寿命。

4 结 论

(1)随着骨架直径的增大,气体温度受入口速度变化的影响越来越小,固体温度的峰值向下游移动;对于Kelvin模型,当d为0.35 mm时,固相温度存在一个明显的峰值,在峰值上游,固相温度随着入口速度的增加而降低,在峰值下游,固相温度随着入口速度的增加而增加,表明低流速粗骨架时,固体内部的温度梯度最大。

(2)骨架直径越小,当量比的变化对温度分布的影响越小,越有利于多孔介质的稳定工作,但骨架较细时,出口处气/固两相的温度均较低,影响了多孔介质的辐射效率。

(3)在同样工况下,与Kelvin模型相比,W-P模型在燃烧区拥有更加均匀的固体温度分布,表明采用W-P模型制得的多孔介质面板具有更长的服役寿命。