开敞式进水池喇叭口悬空高度对吸气涡的影响

黄先北，方 涛，郭 嫱，陈徐睿，庞凯文，仇宝云

(扬州大学 电气与能源动力工程学院，江苏 扬州 225127)

开敞式进水池是中小型泵站中重要的水工建筑之一，进水池的设计通常会影响整个进水池流态的情况，当流态较差时，会形成吸气涡[1-2]。吸气涡的产生会导致泵装置产生震动、噪声，严重时还会发生空蚀，极大地影响了整个泵站运行的安全稳定[3-4]。因此，如何合理地设计进水池结构参数，减轻或抑制吸气涡形成至关重要。

近年来，国内外许多学者对泵站进水池的吸气涡进行了大量的研究。一方面是吸气涡试验观测，主要是采用粒子图像测速法（particle image velocimetry，РIV）[5-6]，其对模型的透明度有一定的要求，当水流混浊时会影响精度，且成本昂贵。另一方面是吸气涡的数值模拟，吸气涡的数值模拟主要采用雷诺平均法（Reynolds-averaged Navier-Stokes，RANS）[7-9]和大涡模拟（large eddy simulation，LES）[10-11]，其中LES的计算精度高，这导致其计算量偏高。Huang等[12]通过对比不同的模型，最终提出采用分叉模型（bifurcation model，BM）和简化的耦合水平集与流体体积方法（simple coupled level-set and volume-of-fluid method，S-CLSVOF）对吸气涡进行数值模拟的效果较好，该方法能够完整地再现泵站进水池吸气涡和精确地捕捉气液交界面。

在泵站进水池结构尺寸优化方面，许多学者采用单因素或多因素的方式，研究了喇叭口悬空高度、后壁距和淹没深度等参数对进水池中流态的影响[13-15]。其中，资丹等[16]采用了响应面的方式研究了悬空高度、后壁距和淹没深度之间的交互作用，发现悬空高度和后壁距对进水池的流态影响较大。

然而，上述研究侧重于进水池的流动均匀性，但进水池结构尺寸对吸气涡的影响规律尚不明确。国内外的泵站设计规范[17-18]规定了后壁距与侧壁距的推荐尺寸，但对于悬空高度仅给出取值范围。考虑到悬空高度对进水池流态的影响，并尽可能保证与设计规范的一致性，本文基于BM湍流模型和S-CLSVOF方法，重点研究泵站进水池喇叭口悬空高度对吸气涡的影响规律，并给出合适的悬空高度取值，为泵站进水池设计提供理论依据。

1 CFD模型与方法

1.1 雷诺平均Navier-Stokes方程和BM湍流模型

雷诺平均Navier-Stokes方程如下：

式中，u为速度矢量，t为时间，ρ为流体的密度，p为压强，ν为运动黏度，τ为雷诺应力，St为动量源项。

τ可由式（2）计算：

式中，τd为偏斜雷诺应力，k为湍动能，δ为Kronecker符号。

式（2）可由涡动黏度假设得到：

式中：vt为涡黏系数；S为应变率张量，表示为：

本文采用Lien和Kalitzin[19]修正的BM模型。其基本方程如下：

Рettersson等[20]通过修正涡动黏度公式构建了BM模型：

采用Davidson等[21]提出的修正方式，将涡黏系数修正为 0 ≤νt≤0.09k2/ε。

1.2 S-CLSVOF模型

S-CLSVOF是一种耦合水平集法和流体体积法的简化版本[22-23]。为了便于捕捉气液交界面，引入水平集法（Level-set）的方程：

式（11）～（12）中， ϕ为流场中某点到交界面的无量纲距离，τ为模拟时间， ϕ0为场中某点到交界面的初始距离，x为位置矢量，S为喇叭口淹没深度。

由于 ϕ是用于确定交界面的，所以可以用 ϕ表示表面张量：

式中，σ为表面张力系数，其余量定义如下：

式（14）～（15）中： γ=1.5xΔ，xΔ为距离交界面最近的网格尺度； κ为自由曲面曲率。

为了保证质量守恒，沿用流体体积法（volume of fluid，VOF）。本文采用OpenFOAM-2.2.2，其液相体积分数输运方程为：

式中， αl为液相体积分数，uc为压缩速度。

两相采用Mixture模型，二者速度与压力相同。

1.3 进水池3维模型尺寸

根据文献[18]标准设计进水池的几何尺寸，如图1所示。进水池的长度为1 612.5 mm（＞10D，D为喇叭口直径），宽度为300.0 mm（2D），D为150.0 mm，吸水管直径为100.0 mm，吸水管侧壁距为150.0 mm，后壁距为112.5 mm（0.75D）。由文献[24]可知，吸气涡存在比尺效应。为减小比尺效应的影响，本文保证雷诺数Re和弗劳德数Fr相同，定义见式（17）、（18）：

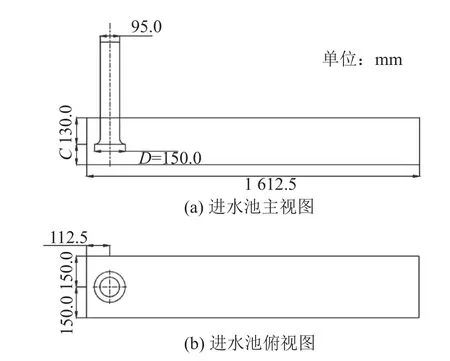
图1 进水池模型尺寸Fig.1 Model size of intake

式中，u为喇叭口进口速度，g为重力加速度。

为此，固定喇叭口淹没深度为130 mm（0.87D），流量为0.016 7 m3/s。根据文献[18]，喇叭口悬空高度C取值为0.3D～0.5D，为进一步分析低悬空高的影响，本文将研究范围拓展为0.2D～0.5D，其中，各方案的参数设置见表1。

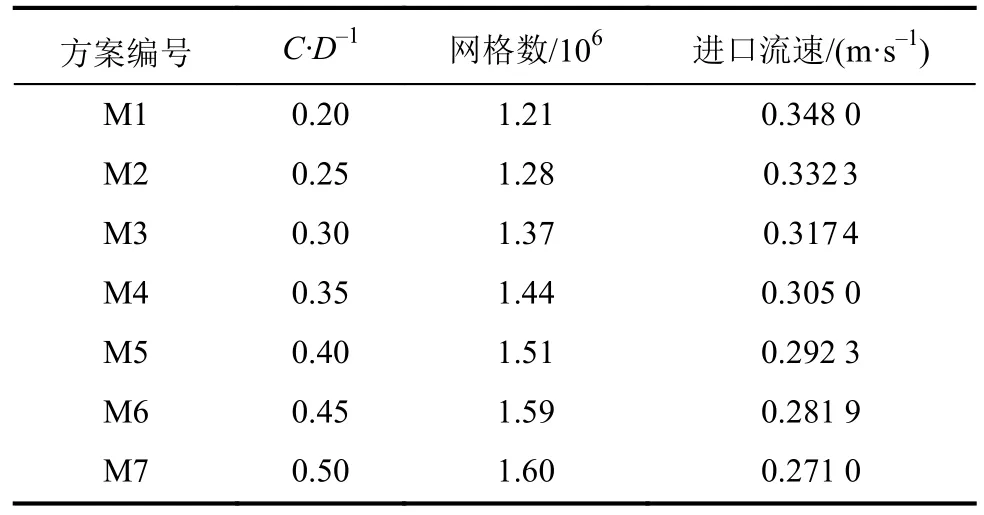
表1 各方案的参数设置Tab.1 Parameter setting of each scheme

1.4 网格、边界条件与数值算法

将模型分为3个计算域，可以得到两个交界面，分别为水气交界面和水域与管道域交界面（图2）。交界面采用任意网格交界面（arbitrary mesh interface，AMI）[25]。出口采用流量出口，体积流量均设定为0.016 7 m3/s；进口给定均匀来流速度，见表1；空气域上边界为总压边界，设定为大气压力；其余边界均为固壁面。压力-速度耦合求解采用РISO（pressure-implicit with splitting of operators）算法，梯度与散度项采用二项精度的“Gauss linear”格式，时间步长为1×10-4，模拟时间为20 s。

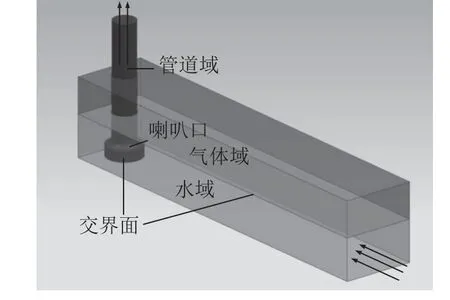
图2 进水池3维模型Fig.2 Three-dimensional model of the intake

1.5 数值模拟方法可靠性验证

为了验证本文数值模拟方法的可靠性，采用文献[26]公开的数据进行验证。需要说明的是，文献[26]为了更好地观测吸气涡，将进水管向进水池侧壁偏移了10 mm。此处基于偏移后的模型进行计算，取10.0～15.5 s内的结果作时间平均。

图3所示为选取线段上的速度分布。在喇叭口下方15 mm处选取线段如图3（a）所示，模拟所得该线段上z方向上的速度分量uz的分布与试验值趋势一致。

图3 选取线段上的速度分布Fig.3 Velocity distribution on the sampling line

根据文献[12]，采用 αl=0.95的等值面可以较好地显示吸气涡的形态，如图4（a）所示。与试验结果（图4（b））对比可见，数值模拟较好地捕捉到了吸气涡的形态。因此本文采用的数值模拟方法是可靠的。

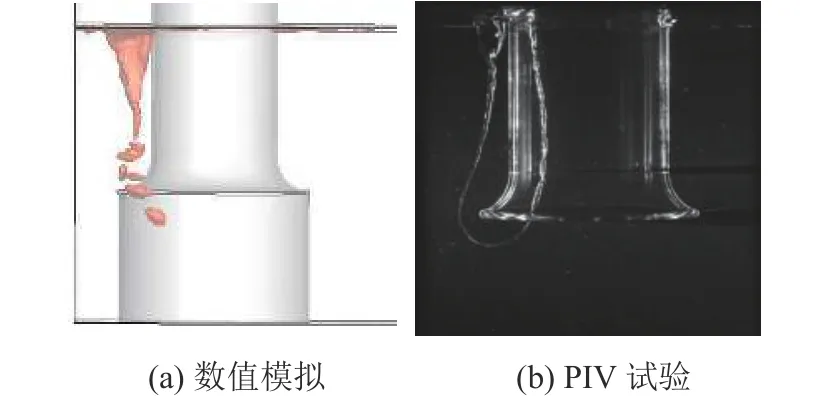
图4 吸气涡在数值模拟与PIV试验观测的对比Fig.4 Comparison between numerical simulation and PIV experimental observation of air-entrained vortex

2 试验结果与分析

2.1 吸气涡形态与相对吸气率的关系

为定量分析吸气涡程度，采用相对吸气率描述，其定义为[27]：

式中，β为吸气率， αlo取计算域出口面的液相体积分数。

选取M1、M3、M4、M5和M7共5种方案在第12 s时的吸气涡形态进行对比，结果如图5所示。显然，M1的吸气率最高，M4的吸气率最低。由此可见，图5所观测的吸气涡形态可由计算域出口的相对吸气率定量体现。

图5 不同方案吸气涡形态对比（t=12 s）Fig.5 Air-entrained vortex shape of different schemes (t=12 s)

从水面到喇叭口的吸气涡形态来看，M1（C=0.2D）的吸气涡大小均相对于其他方案的吸气涡更显著。进水管内的吸气涡呈破碎状，且随着悬空高的增加，吸气涡呈减小的趋势，在M4时基本消失，而随后在M5～M7（M6未显示）中重新出现，但仍小于M1～M3（M2未显示）。

2.2 相对吸气率随悬空高度的变化规律

计算每个方案、每个时刻的相对吸气率，如图6所示，可见相对吸气率随时间变化较大，因此采用离散时刻来表征某一方案整体的吸气涡程度不合理。由图6可见，M1的吸气率在10 s后达到类似周期性的变化规律，且其余方案的规律相近。因此，对10 s后的β求平均值 β。

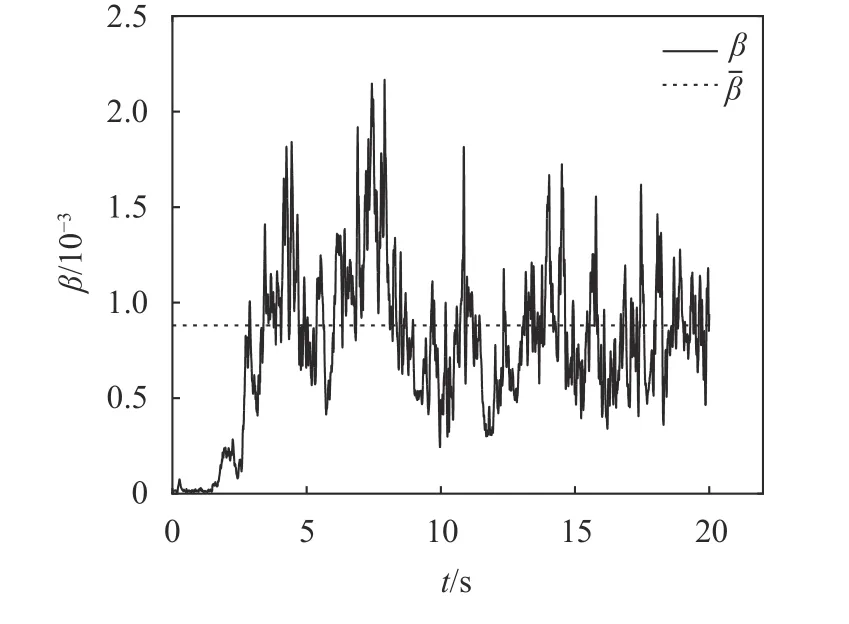
图6 相对吸气率随时间的变化（M1）Fig.6 Variation of relative air-entrainment rate with time (M1)

平均相对吸气率 β随悬空高度的变化规律曲线，如图7所示。从图7可以看出，平均相对吸气率整体随悬空高度增加而降低，但在M4（C=0.35D）方案吸气率突降，其原因将在后文进一步分析。从泵站设计的角度来看，尽管M4与M7的吸气率均较低，但悬空高度的提高将使相同条件下的泵淹没深度降低，从而降低泵装置的空化性能。综合而言，M4优于M7。

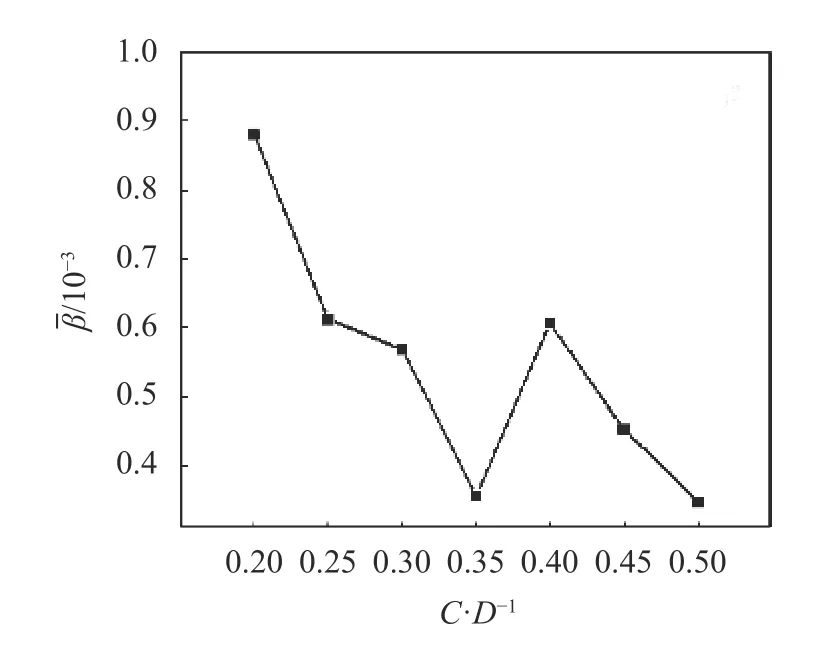
图7 随C的变化规律曲线Fig.7 Variation curve ofwith C

2.3 吸气率突降原因分析

涡量是表征流体旋转运动的物理量之一，通常情况下用于表示流体旋转运动的强度。下文从涡量的角度分析导致M4相对吸气率降低的原因。

图8为M1、M3、M4、M5、M7在第20 s时喇叭口上方5 mm处的涡量在z方向上分量Ωz云图。从图8可看出，涡量集中在某些区域，但其位置并不一致。此外，涡量集中区域分正值和负值两类，这是因为有2个吸气涡进入进水管（图5），且旋转方向相反。对比5种方案的涡量分布，发现M4和M7的涡量峰值区域更小，说明漩涡更弱，这与前文分析一致。

图8 喇叭口上方5 mm处涡量分布（t=20 s）Fig.8 Vorticity distribution 5 mm above the bell mouth (t=20 s)

为定量显示每个方案涡量随时间的变化规律，计算进水管内距离涡量峰值|Ωz|max所在位置10 mm的圆形区域内的均值，并对其作时间平均，如图9所示。对比图7可知，涡量均值随悬空高度的变化规律基本与吸气率均值变化规律一致，说明涡量可定量体现吸气涡的强度，且强度越大吸气率越高。

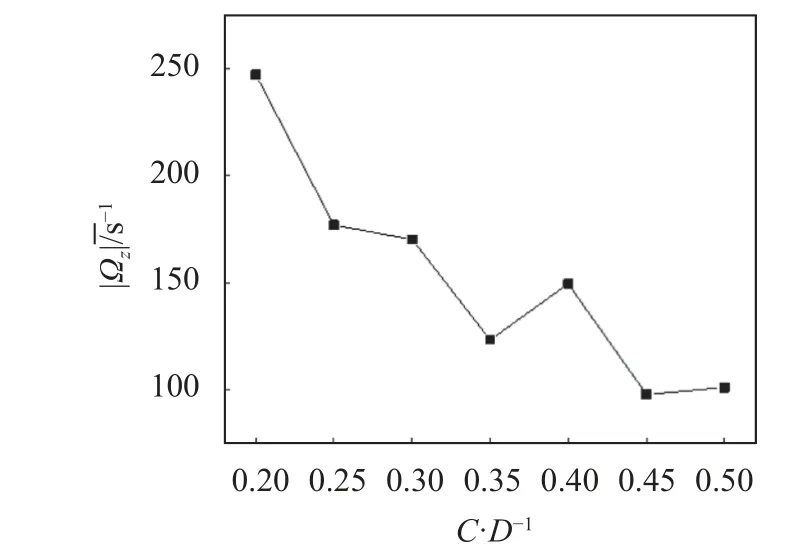
图9 各方案| Ωz|的均值Fig.9 Mean value of | Ωz | of each scheme

为进一步分析吸气率随悬空高度变化规律的内在机理和平均相对吸气率突降的原因，基于式（20）所示的涡拟能输运方程进行分析：

式中：ωx、ωy、ωz表示涡量x、y、z的分量；T1为倾斜项，表征漩涡受到的倾斜作用；T2为拉伸项，表征漩涡受到的拉伸作用；二者均体现了涡拟能的变化率[28]。

由文献[29]可知，T2是导致吸气涡形成的主要原因。为方便数据处理与研究，对T2用进行无量纲处理。图10为M1、M3、M4、M5、M7在第20 s喇叭口上方5 mm处的无量纲化的T2分布。

图10 喇叭口上方5 mm处T2的分布（t=20 s）Fig.10 Distribution of T2 at 5 mm above the bell mouth (t=20 s)

由图10可见，各方案进水管中的T2值均在200以上。其中：M1的T2值在200以上的区域几乎充满整个管道；其他4个方案的T2值在200以上的区域集中在管道的一侧，而这4个方案的分布也略有不同。由T2的峰值可知，随着悬空高度的增加，T2整体呈下降趋势，但在M4出现突降，与图7规律一致。由此可见，不同方案下吸气涡形成后，吸气率取决于漩涡受到的拉伸作用，其中M4的拉伸作用相比M3与M5发生突降，从而导致相应的涡拟能变化率降低，最终导致漩涡强度下降，吸气率降低。

3 结 论

本文基于BM模型和S-CLSVOF界面追踪方法，采用OpenFOAM-2.2.2进行数值模拟，研究了泵站进水池喇叭口悬空高度对吸气涡的影响，得出以下结论：

1）分析不同时刻的吸气涡形态，发现吸气涡的大小和进水管内相对吸气率β呈正相关。

2）通过计算各方案进水管出口处的相对吸气率，发现相对吸气率基本随悬空高度的增加呈下降趋势，但当C=0.35D时，出现突降。

3）管内涡量的大小体现了吸气涡的程度，与相对吸气率的规律一致。另外，涡拟能输运方程中拉伸项T2决定了涡量的变化，从而影响平均相对吸气率，是导致平均相对吸气率在C=0.35D处出现突降的关键因素。

4）考虑到吸气涡程度与泵的安装，M4方案（C=0.35D）为最优选择。