计及分布式电源的复杂配网潮流特性仿真分析
崔艳林, 林旭, 郭俊宏
(广东电网有限责任公司电力调度控制中心,广东 广州 510600)
0 引 言
分布式电源的高渗透率接入会直接影响当前电网网架结构、电网潮流分布以及电网线损[1-2]。为适应分布式电源接入配电网架结构,研究计及分布式电源的复杂配网潮流特性具有现实意义[3]。电网网架结构潮流特性分析是以数学分布方法为工具,以电网网架结构内电源、负荷节点分布与电压电流等信息为基础的电气分析方法,经潮流特性分析能大致确定整体电网网架结构的运行状态[4]。文献[5]提出了考虑等效拟合特性的输配电网全局潮流特性分析方法,构建潮流分析模型,在迭代过程中计算拟合函数,实现潮流分析。该方法主要应用于电网内支路阻抗比较小的情况,随着支路阻抗比提升,方法的鲁棒性有所下降。文献[6]研究了含分布式发电配电网模糊潮流特性分析方法,确定电网内分布式电源与负荷数据的嵌套特性,采用优化的前推回代法分析潮流特性。该方法针对三相不平衡等复杂电网的应用性较差。考虑计及分布式电源的电网网架结构内,极易产生三相不平衡状态,导致电网复杂性显著提升。因此,进行计及分布式电源的复杂配网潮流特性仿真分析,通过试验验证潮流特性分析的准确性。
1 计及分布式电源的复杂配网潮流特性研究
1.1 分布式电源接入配电网的潮流改变
图1(a)为单电源电网网架结构,此结构内节点1为平衡节点,是此网架结构内仅有的电源节点。箭头所示为潮流方向,且潮流方向为单相。在分布式电源接入电网网架结构的条件下,即图1(b)所示,单电源电网网架结构转变为多电源电网网架结构,除节点1外,接入的全部分布式电源同样成为此电网网架结构内的电源节点,均会向电网内注入功率。基于此,在多电源电网网架结构内,潮流为双向流动。
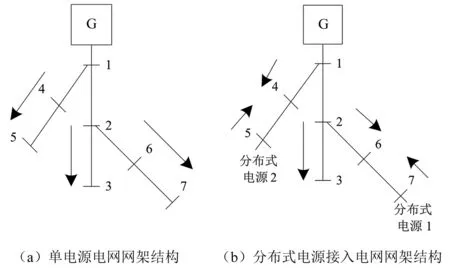
图1 电网网架结构示意图
1.2 潮流特性分析
1.2.1 潮流方程
依照电路学的节点电压方程,描述三相电网内节点注入的电流:
(1)
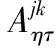
在功率方程内引入式(1),能够得到:
(2)
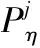
(3)

1.2.2 复杂配网直接潮流算法
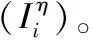
(4)
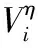
(5)
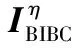
(6)
(7)
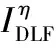
2 仿真验证
以某包含11个节点的复杂(三相不平衡)配电网网架结构为仿真对象,在MATLAB仿真软件内构建仿真对象拓扑结构模型,如图2所示。
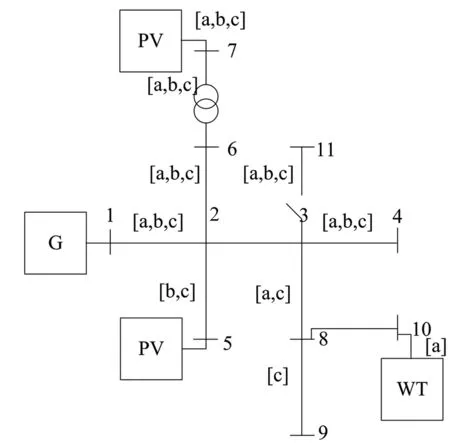
图2 仿真对象拓扑结构
图2内:仿真对象支路6、7为变压器支路;支路3、4、5、8、9、10为开关支路,其中包含3个分布式电源,分别位于支路5、7和10处。设定节点1为参考节点,以其为仿真对象潮流特性分析的相位参考点。设定迭代误差为Δx1、Δx2和Δx3。
2.1 高阻抗比支路鲁棒性仿真
为验证本文方法在分析仿真对象高阻抗比支路的鲁棒性,在仿真对象内随机选取某条支路,仿真过程中选取节点3与节点4之间的支路。采用本文方法获取高阻抗比支路的鲁棒性结果如表1所示。

表1 高阻抗比支路的鲁棒性
分析表1可知:随着所设置阻抗比的提升,本文方法均可靠收敛,同时迭代次数与分析过程所耗费时间具有较高的稳定性。由此得到,本文方法在面对仿真对象(包含高阻抗比支路)的条件下具有较好的鲁棒性。考虑分布式电源的下垂特性与负荷静态特性,在三相不平衡孤岛电网网架结构中计算了潮流特性,可以在高阻抗增加的情况下,保持稳定的计算能力。
2.2 对比分析
为进一步验证本文方法的应用性能,选取考虑等效拟合特性的输配电网全局潮流特性分析方法和基于参数化隶属度匹配函数的含分布式发电配电网模糊潮流特性分析方法作对比,分别定义为方法1和方法2。比较两种方法和本文方法对于仿真对象各节点电压幅值计算的偏差度,所得结果如图3所示。
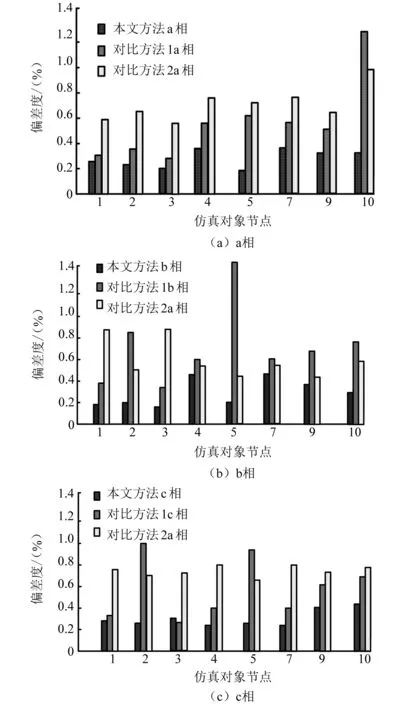
图3 不同方法电压幅值计算结果的偏差度
采用本文方法分析仿真对象潮流特性时,仿真对象内各节点电压幅值分析结果的偏差度控制在0.5%以内。综上所述,可知对比得到本文方法与其他两种方法相比具较高的分析精度。
3 结束语
潮流特性分析是针对给定的电网结构与参数等条件,分析其各部分稳定运行状态的过程。考虑电网内支路阻抗比提升的问题,进行了计及分布式电源的复杂配网潮流特性仿真分析。针对包含分布式电源的复杂配电网,构建潮流方程分析其潮流特性。通过仿真分析,证明了本文方法的收敛较好,计算耗时平均约为0.22 s,且偏差度较低,说明该方法可以更好地使用于分布式电源接入复杂配网环境中的潮流计算。本文为分布式电源控制提供一定参考依据。

