基于广域网和多Agent的高压电网站间实时控制方法

李永光, 黄辉, 常星, 王中伟

(1.国网新疆电力有限公司,新疆 乌鲁木齐 830000; 2.中国科学院沈阳计算技术研究所有限公司,辽宁 沈阳 110168)

0 引 言

随着我国经济建设的快速发展,用电量成倍增长,部分城市用电量远远超出城市自身发电量,造成电力资源紧张。在电力资源需大于供的背景下,高压电站远程调配控制的准确性与稳定性给高压电站间控制提出了挑战。面对高强度的高压调配数据处理,现有控制方法普遍采用单信息处理分析与多任务资源差量分析方法,主旨在于提高高压电资源调配的合理性。实际上电能调配的重复计算过程产生的时间差量是造成现有算法控制精度低、实时性差的关键因素。

基于上述思想,结合控制电站间的广域网算法与多Agent的分布特性［1-2］,对控制方法进行优化,提升算法精度与高压电站间实时控制效果。

1 基于广域网和多Agent的高压电站间实时控制方法实现

1.1 基于广域网和多Agent的控制信道模型建立

根据高压电控制过程中的高压数据多样性特征,为了避免不同高压参量数据传输过程中的相互扰动,采用广域网+多Agent的优化方案［3］,将不同特征的高压数据参量划分为多个Agent数据点,在广域网整体空间下,组建Agent多点控制网络［4］,构建专有通信信号模型。具体优化过程可根据对应实现功能的不同,划分为两个阶段,分别为编码生成阶段与信道传输阶段。

编码生成阶段:基于广域网整体数据控制协议,采用Polar编码作为优化编码方式［5-6］,将选取的编码方式应用于信道E,通过对信道构成参量的归一计算［7］,如图1所示。图1中:m1、m2为不同的优化信道;x1、x2为数据交互状态的不同种类;E2为另一种原始信道;y1、y2为x1、x2对应的编码。E2的编码生成系数对应信道转换系数为:

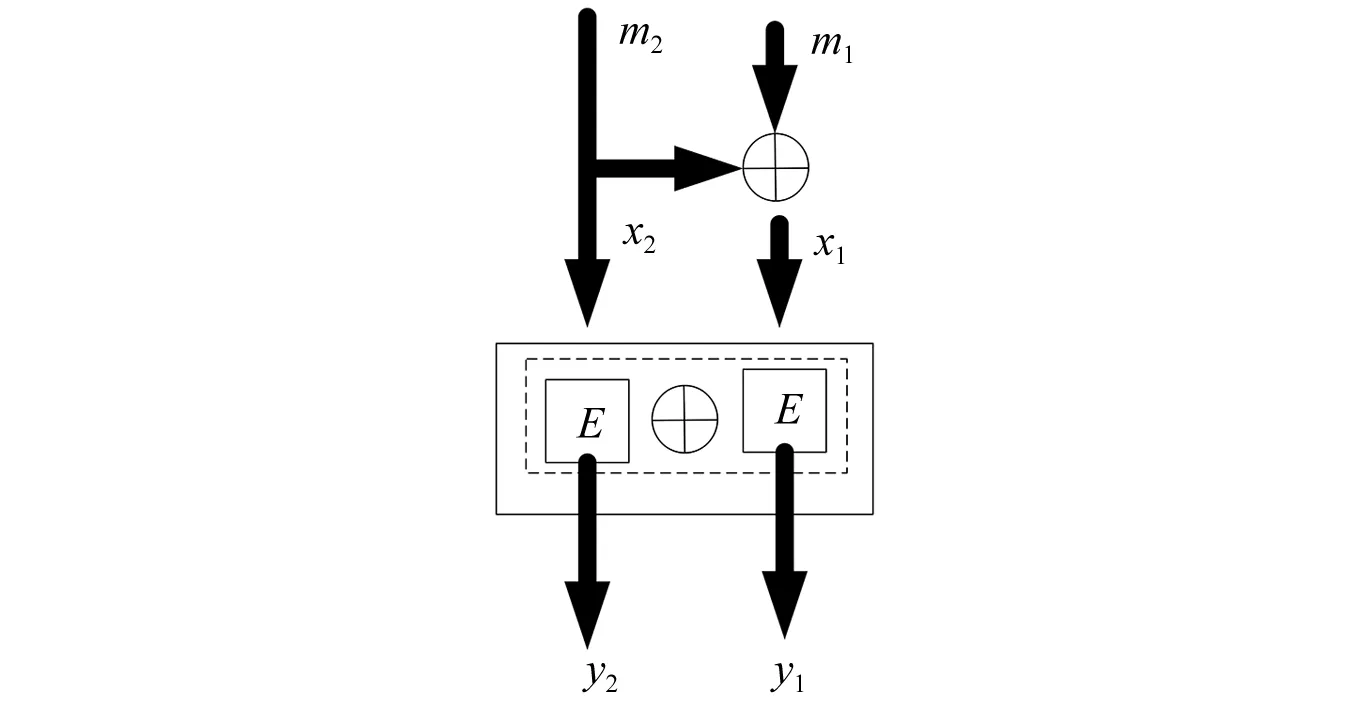
图1 二次编码信道优化模型

E2=(y1,y2|m1,m2)=E(y1|m1⊕m2)E(y2|m2)

(1)

式中:EK为信道对应优化信道系数k的约束条件。EK:XK→YK,其中K=2k且k≥0。若将信道编码条件量设定为k=1,其编码生成系数对应信道约束为E2:X2→Y2。在这个过程中,编码会对信道进行数据二次重组,得到二次编码优化对应信道关联系数:

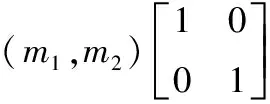
(2)

式中:F为矩阵相似变化系数。根据编码二次优化对应的信道构建关系,二者之间为映射关系,整个映射关系可通过函数式描述为:

(x1,x2)→(m1,m2)H2

(3)

通过代入广域网控制信道E的生成序列(x1,x2),获得一个与原编码生成信道E对应的新的信道生成序列(m1,m2)。所对应的映射序列H2为:

(4)

若将信道编码条件量设定为k=2,根据此刻的广域网信道矢量状态［8］,可得到信道约束为E4:X4→Y4,如图2所示。

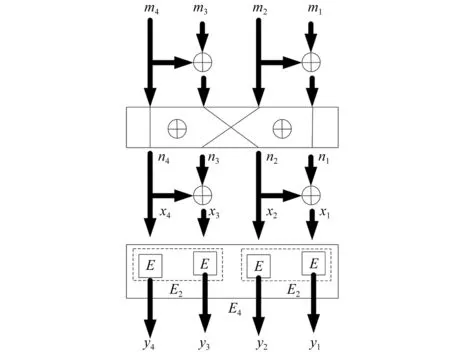
图2 四信道编码优化模型

图2中:n1、n2、n3、n4为不同信道编码优化过程中所对应的编码分布距离;m3、m4为不同的优化信道;x3、x4为数据交互状态的不同种类;y3、y4为x3、x4对应的编码。

此时,Polar编码优化下的信道E4对应转换系数为:

(5)

信道传输阶段:上述优化所得信道中包含4种数据交互状态,分别对应两种发送状态与两种接收状态,为了保持两种发送关系与两种接收关系的平衡［9-10］,对信道编码关系差值计算,计算后得到Polar编码优化信道的输出关系为:

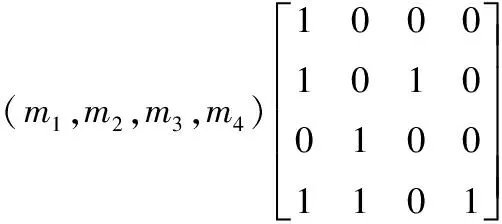
(6)

在上述优化关系的基础上,将广域网原始信道E的生成序列(x1,x2,x3,x4)与其对应生成的全新生成序列(m1,m2,m3,m4)的映射关系重新表述,其表达式:

(x1,x2,x3,x4)→(m1,m2,m3,m4)H4

(7)

其中:

(8)

通过计算求解H2与H4之间的关系,可以关联得到:

HK=BKF⊗k

(9)

式中:BK为信道构成过程中编码转换的比特翻转矩阵,K=2k,k≥0;F⊗k为克罗内克积［11］,F⊗k=F⊗F(k-1)。经过上述一系列计算可以得到K信道Polar编码优化模型,如图3所示。

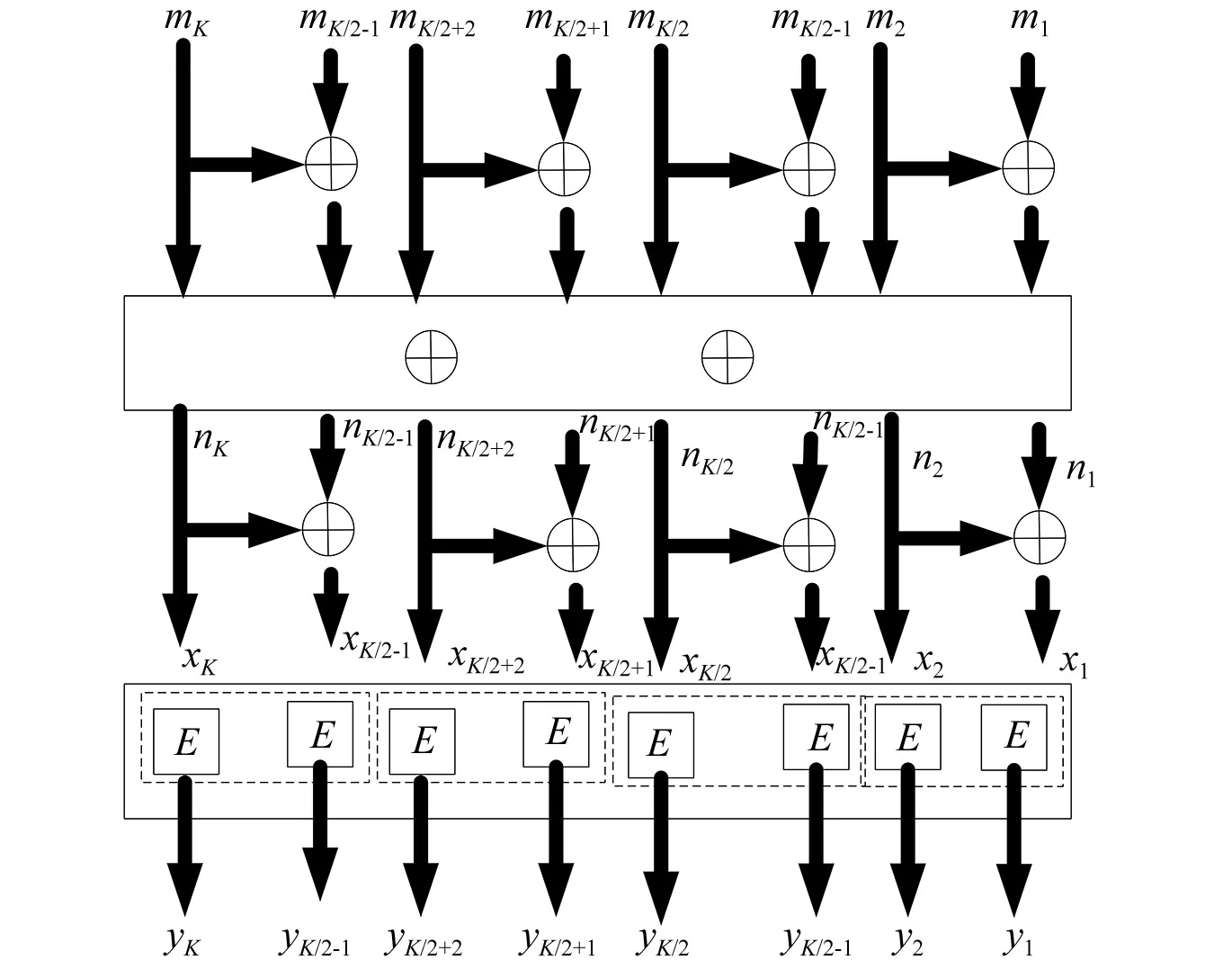
图3 K信道Polar编码优化模型

经过对计算过程的整理,可以得到EK与EK之间信道传输编码优化关系为:

(10)

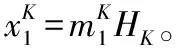
1.2 高压电站间控制补偿策略

完成高压电站间控制第一步信道编码优化后,考虑到高压电传输效率与电站存储效率之间的不平衡性,一般情况下需要通过电站效率补偿计算,提升电能控制数据与存储电能传输数据之间耦合系数［12］,达到最佳的数据结合效果。

基于上述思想,补偿计算中采用Agent多点分布补偿策略。具体控制补偿策略操作过程为:将控制数据中高压控制总值平均化计算,得到此时控制状态下高压控制总偏差值的Agent最小系数。根据当前高压电站电能存储状态与最大供电次数之间的函数关系,建立Agent多点分布补偿模型,实现对控制数据参量变化的实时跟踪,确认高压控制过程中的补偿位置与补偿系数。

(1) 高压控制的Agent平均最小差值计算公式,可以通过目标函数关系的方式描述为f1(x):

minf1(x)=

(11)

式中:Psch(i)、PPV_sch(i)、Pf_sch(i)、Pb_sch(i)分别为1～4次补偿点的高压存储量补偿函数。

(2) 高压电站电能存储状态与最大供电次数之间函数关系对应的最小目标函数f2(x)为:

minf2(x)=minNb

(12)

式中:Nb为高压存储量约束。

(3) 进一步计算,得到Agent多点分布控制补偿的最大目标函数f3(x)为:

maxf3(x)=maxQSOC(N)

(13)

上述计算中,考虑了高压存储量约束、高压输出量约束与高压总值均量约束三方面的约束条件。利用Agent多点分布计算的方式,对控制数据点进行补偿计算。利用Agent多点分布计算的线性增益模型,提升高压电数据的控制能力与控制总量。

在补偿优化计算后,控制电站间数据中的高压数据状态分为:数据跟踪状态与数据更新状态两种,其中数据更新状态参照数据补偿结果完成输出更新。期间受到补偿数据与原始数据之间的差异化确认影响,会产生一定数值的偏差,需要根据补偿数据值,相应调节更新阈值的自适应控制系数。

1.3 高压电站间自适应控制算法

对高压电站间控制更新阈值自适应计算,以图4中高压控制线路为例,在S-M位置上S处初始控制电流数据对应的更新阈值定义为零序电流II,在此基础上完成高压电站间控制更新阈值自适应计算。

图4 高压电站间控制数据模型

假设S位置上的侧向控制系数所受到的更新正序阻抗与负序阻抗相等,并且满足更新阈值阻抗数据为0时的系数大于正序阻抗对应值。根据广域网控制数据自适应调整机制与Agent节点数据流整定策略,S位置上0值阻抗对应零序电流Ⅱ的更新阈值自适应整定计算式为:

(14)

(15)

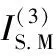
2 应用测试

测试基于广域网和多Agent的高压电站间实时控制方法的实际应用性能。参与测试的除提出控制方法外,还包括基于神经网络的高压电站间控制方法与大数据分析的高压电站间控制方法,分别标记为对比组1与对比组2。

2.1 设置测试条件

为了保证测试过程中的信道处理数据速度与传输速度的一致,将三种控制方法的信道编码方式全部设置为Polar编码。将三种算法同时接入测试环境,由仿真测试工具根据高压电站运行数据,模拟生成高压数据对其进行数据高压控制性能测试。在测试过程中,3种测试方法运算产生的错误与校验误差将转换为控制扰动噪声,对应增加控制复杂系数,增大控制方法的运算成本,3种控制方法扰动处理复杂度如表1所示。

表1 控制方法扰动处理复杂度对比

由表1可以看出,相同Polar编码的条件下,在高压电站数据运算复杂度设计上,提出控制方法的计算成本更低,对应得到的计算速度最快。

2.2 高压电扰动噪声控制效果分析

实际应用中的高压数据噪声分布具有不确定性,为了获得更加真实的控制结果,将上述测试过程中获得的数值按照噪声分布特点释放,从而获得符合不确定性分布的高斯噪声扰动控制曲线,如图5所示。由虚线可以更加直观地发现,提出控制方法中的Agent多点分布计算能够更好地在广域网环境控制运算复杂系数,降低运算成本。

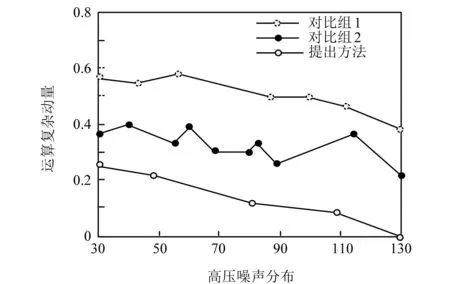
图5 不确定性分布的高斯噪声扰动控制曲线

2.3 电站间数据控制效果分析

将上述测试结果应用到控制方法的全局控制测试中,生成不同控制异常缺额数据下的控制方法测试数据,对应异常数据的缺额数值分别为30 Mvar、55 Mvar、80 Mvar、105 Mvar、130 Mvar、155 Mvar。三种控制方法对应控制高压母线数据,采用30万千伏的BUS32母线电压,全局控制测调度效果对比结果详见表2。

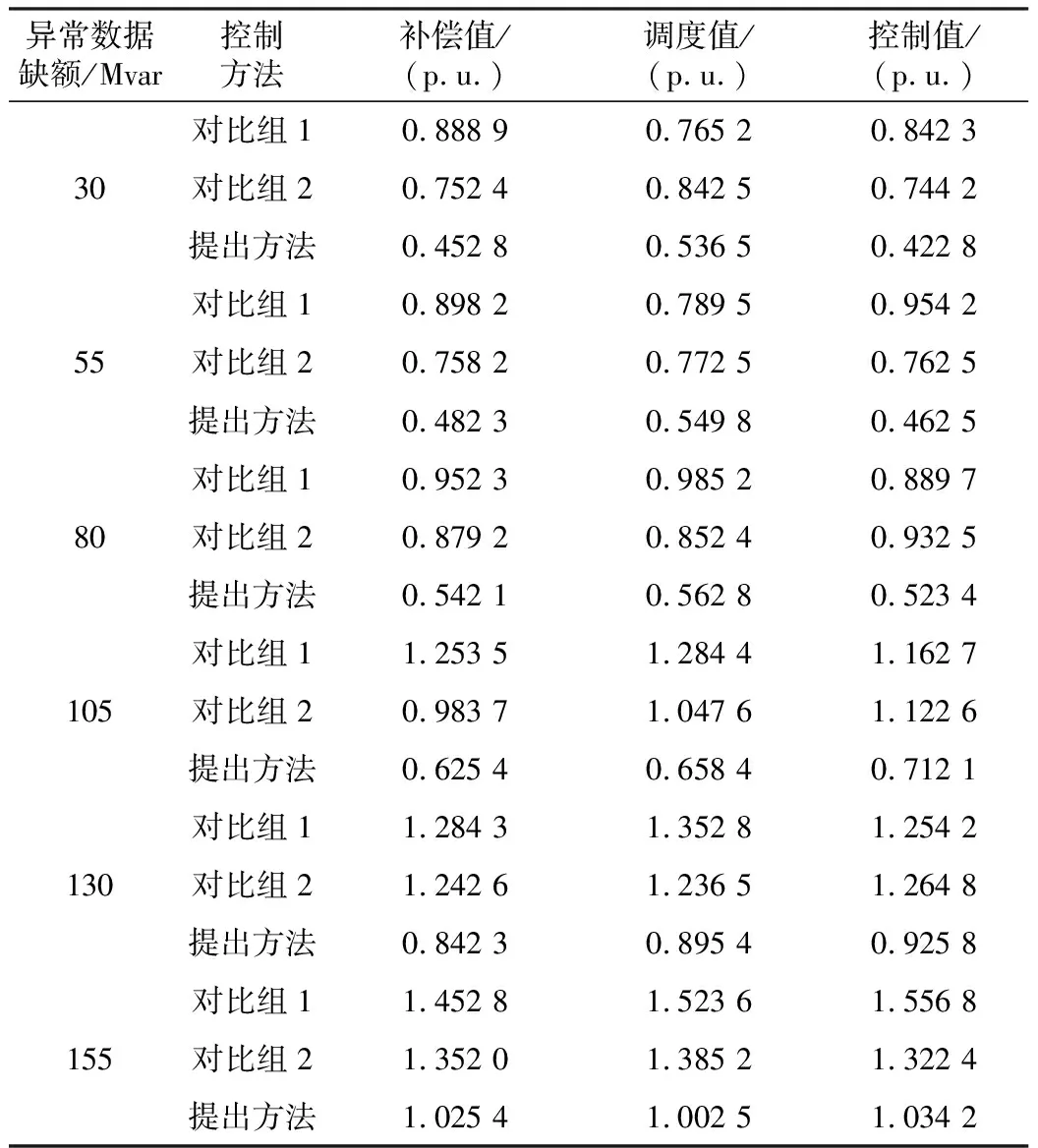
表2 高压电站数据异常状态下三种控制方法的数据调度效果

由表2可以看出,当高压输出电压异常波动时,对应电站间控制数据会出现数据调度误差,误差系数值大小根据电压异常系数动态波动。整体来看,三种控制方法都能够将调度系数控制在一定范围内,但整体数值均向上浮动。相比之下,提出方法的调度控制效果在三种控制方法中最好。在不同缺额条件下,提出控制方法能够将增长19.6%的缺额数据控制在1.1以下,结合30万千伏的控制量,将调度数据转换为控制精度数据,得到三种控制方法的全局控制精度详见表3。对应控制性能如图6所示。

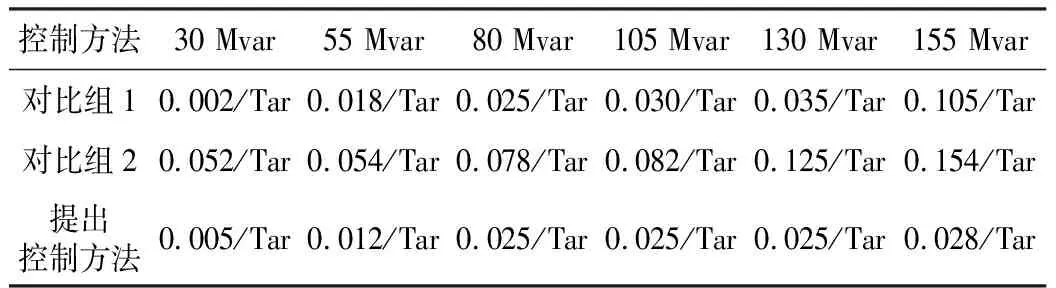
表3 30万千伏高压电站间控制精度对比

图6 30万千伏下电站间数据控制运算性能

从表3与图6可以看出:

(1) 在控制高压数据满足实际使用30万千伏处理时,对比组1控制方法能够将控制精度最大控制在0.105,对比组2控制方法能够将控制精度最大控制在0.154,表明当高压数值达到30万千伏时,对比组2的控制精度不如对比组1的控制精度,正好证明了高压控制的不确定性。相比之下,提出的控制方法能够将控制精度最大控制在0.028,控制精度更高。

(2) 结合表2数据分析表3可以发现,三种控制方法中,提出方法的自适应性最好,控制效果稳定性最佳。

3 结束语

本文提出一种基于广域网和多Agent的高压电网站间实时控制方法。根据高压电站电路特点,结合高压控制网络数据控制特征,从高压数据与网络结构入手,对控制数据信道编码与控制策略优化计算。在满足高压电站基础参量的情况下,利用广域网与多Agent算法,修正控制参量,实现实时高精度控制效果,其实用性意义在于可以有效应对高斯噪声扰动,保证不同工况下的数据调度效果,可以在相关领域大加推广。

但提出方法存在一些未解决问题,如高压电路与控制数据之间时差问题,需要在未来的研究中,不断增加Agent分布数量,获取更多数据来减小时间误差带来的控制误差,将方法调试到最佳状态。