木窗双端复合精铣加工机床主轴系统的刚柔耦合动力学建模与仿真

任长清,王涛,丁星尘,丁禹程,杨春梅,宋文龙

(东北林业大学 机电工程学院,哈尔滨 150040)

0 引言

欧式木窗双端复合精铣加工机床是加工木窗的重要设备,其加工精度的高低对木窗的质量好坏具有较大的影响,而机床主轴系统的刚度和能否平稳工作是影响加工精度的重要因素。双端复合精铣加工机床的主轴系统是机床直接参与加工的重要部件,而在以往对主轴系统的研究中学者都将主轴部件视为刚性体,但在实际加工过程中,机床主轴系统精度极高,在受力后会有一定程度的变形和弹性振动,因此在对机床的主轴系统进行研究时,要考虑到主轴的柔性变形和振幅大小对整个系统的影响,即应将主轴部件视为柔性体。因此,如何对主轴系统进行有效的动力学分析,建立控制模型,提高铣削精度和工作可靠性,引起了许多学者的重视[1]。

本研究以木窗双端复合精铣加工机床的主轴系统为研究对象,使用Solidworks建立主轴系统的多刚体模型并进行仿真分析,利用Ansys生成主轴部件的柔性体模型并联合Adams进行刚柔耦合模型的仿真分析,对比两者仿真结果,旨在获得主轴为刚性体和柔性体时2种不同的主轴系统的动力学特性,在进行比较后得出结论,为主轴系统的结构优化提供理论依据,以提高加工精度。

1 多刚体虚拟样机的建立与动力学仿真

1.1 三维模型的建立

主轴系统的模型建立是其动态特性分析的重要内容[2],主轴系统主要由主轴、带轮、皮带和轴承等零件组成。本研究使用三维建模软件Solidworks来进行主轴系统的三维模型建立,为方便仿真,建模时省略螺纹、倒角和退刀槽等对仿真影响较小的特征[3-4],主轴系统在机床中为直立固定,主轴总长533 mm,主轴从上到下分为锁紧部分、刀具安装部分、上轴承安装部分、转子部分、下轴承安装部分和带轮安装部分,除锁紧部分外从上到下各轴段的直径分别为50、60、78、50、38 mm;长度分别为115、34、222、30、87 mm,下带轮安装部分连接一带轮,上、下轴承安装部分分别安装有一对角接触球轴承,安装方式为背对背组配安装。主轴系统各零件三维模型建立完成后,将各零件进行配合后完成主轴系统装配体的三维模型建立,如图1所示。

图1 主轴系统三维模型装配图Fig.1 Assembly drawing of 3D model of spindle system

1.2 多刚体虚拟样机的建立

将建立完成的主轴系统三维模型通过Adams中的导入命令导入到Adams中,为了仿真方便,又不影响仿真结果,将模型中的轴承拆去[5],再在Adams中通过Adams Machinery模块重新创建轴承,创建完成后的轴承需要设置刚度、阻尼和预载荷等参数,图2为Adams中默认的轴承参数。

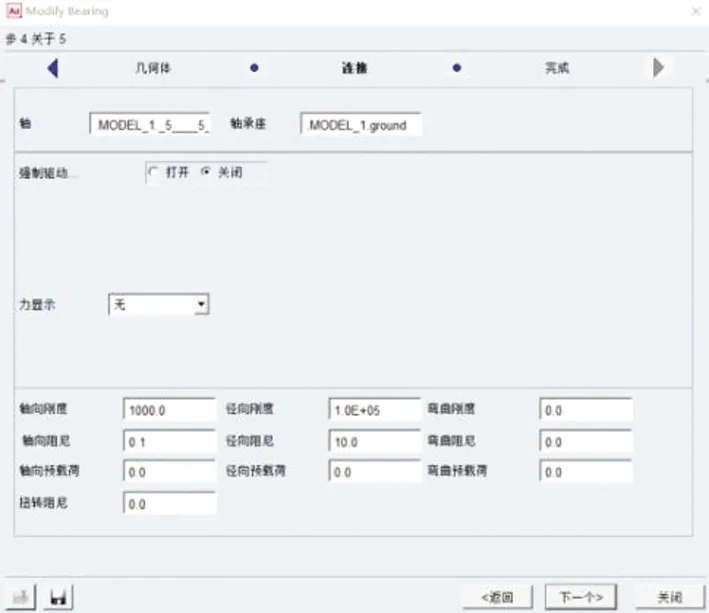
图2 Adams默认轴承参数Fig.2 Adams default bearing parameters

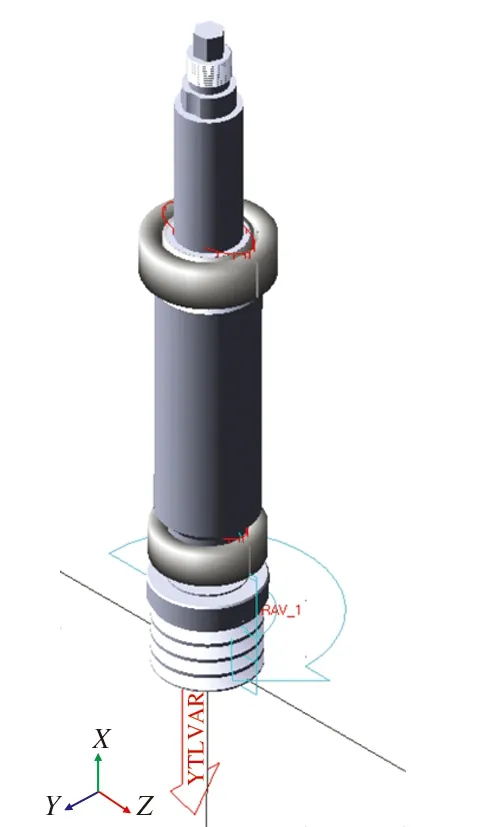
图3 主轴系统多刚体虚拟样机Fig.3 Spindle system multi-rigid body virtual prototype

模型导入Adams后各零件的材料属性为默认设置,需要重新设置主轴和带轮零件材料属性,各零件材料属性见表1。

主轴与带轮之间为键连接,在Adams中使用固定副来表示此连接。另外,在带轮与ground(Adams软件中默认的作为背景或地面)之间添加一旋转副,并在带轮上添加一转速为6 000 r/min的逆时针驱动。建立完成的多刚体虚拟样机,如图2所示,主轴的后端面中心点与坐标系原点重合,重力沿-Y轴方向。

1.3 轴承刚度计算

为了仿真结果准确,需要对轴承参数进行正确设置[6-7],Adams中提供了默认的轴承刚度和阻尼等参数,其中刚度对仿真影响较大,需要进行重新设置,而阻尼对仿真的影响较小,可设为Adams中的默认值。通过Solidworks建立的主轴系统三维模型中的支承轴承为2个角接触球轴承背对背组配安装,而在Adams中的多刚体虚拟样机创建的轴承为单个安装,虽然这2个模型不同,但只需要正确设置Adams中的轴承参数,同样能达到轴承背对背组配安装效果,并不会影响仿真结果。

采用式(1)来计算组配轴承组的轴向和径向刚度。假设其组配的轴承为同型号[8]。

(1)

式中:Ja为组配轴承组轴向刚度,N/mm;m为组配轴承组中轴承1的个数;n为组配轴承组中轴承2的个数;Fa为轴向载荷,N;K为弹性变形综合系数, 对于K,可用式(2)计算。

(2)

式中:Φ为滚动体直径,mm;Z为滚动体数量;α为轴承的接触角,(°)。

本研究所使用的轴承参数见表2。

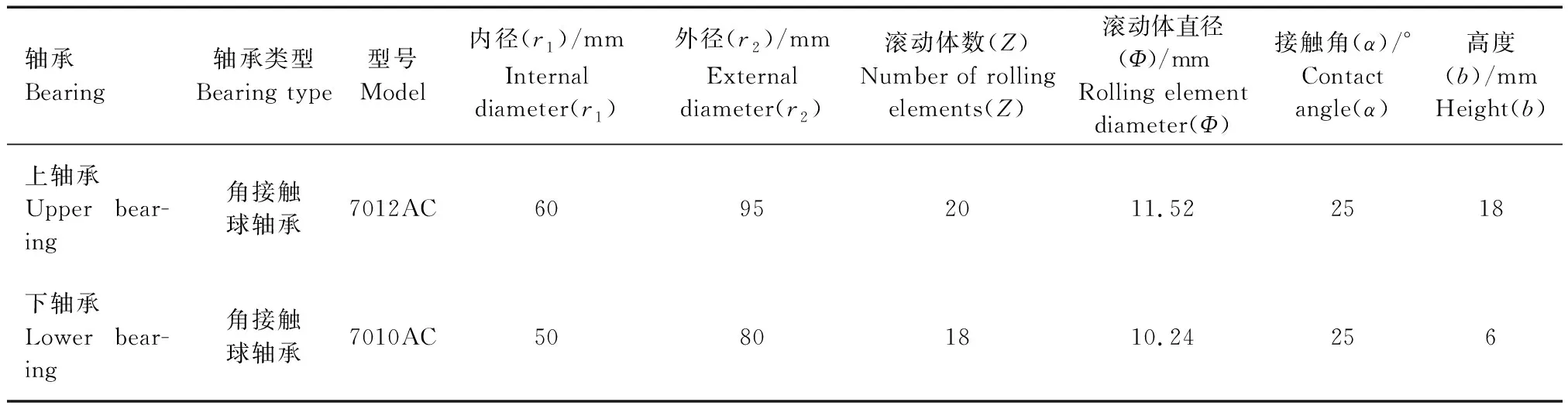
表2 支承轴承的结构参数Tab.2 Structural parameters of support bearings

根据表2中提供的参数计算出上下轴承的弹性变形综合系数K分别为K1=1.10×10-3,K2=1.23×10-3。将K1和K2代入式(1)中,m和n皆为1,轴向载荷(Fa)根据主轴系统的重量给定80 N,得到上轴承的轴向刚度Ja1=11 751.46 N/mm,下轴承的轴向刚度Ja2=10 509.44 N/mm。

径向刚度(Jr)使用式(3)进行计算。

Jr=Jr1+Jr2。

(3)

(4)

(5)

式中:ε为载荷分布系数;Jr(ε) 为径向载荷分布系数;Ja(ε) 为轴向载荷分布系数。

当组配的轴承为同型号,且个数皆为m和n皆为1时,式(4)和式(5)可写为

(6)

于是式(3)可改写为

(7)

在径向载荷Fr、轴向载荷Fa和实际接触角已知的条件下,可根据Frtanα/Fa的计算值从表3中查得ε、Jr(ε)和Ja(ε)。当Frtanα/Fa的计算值与表中所列的Frtanα/Fa不同时,可采用线性内插法计算[8]。

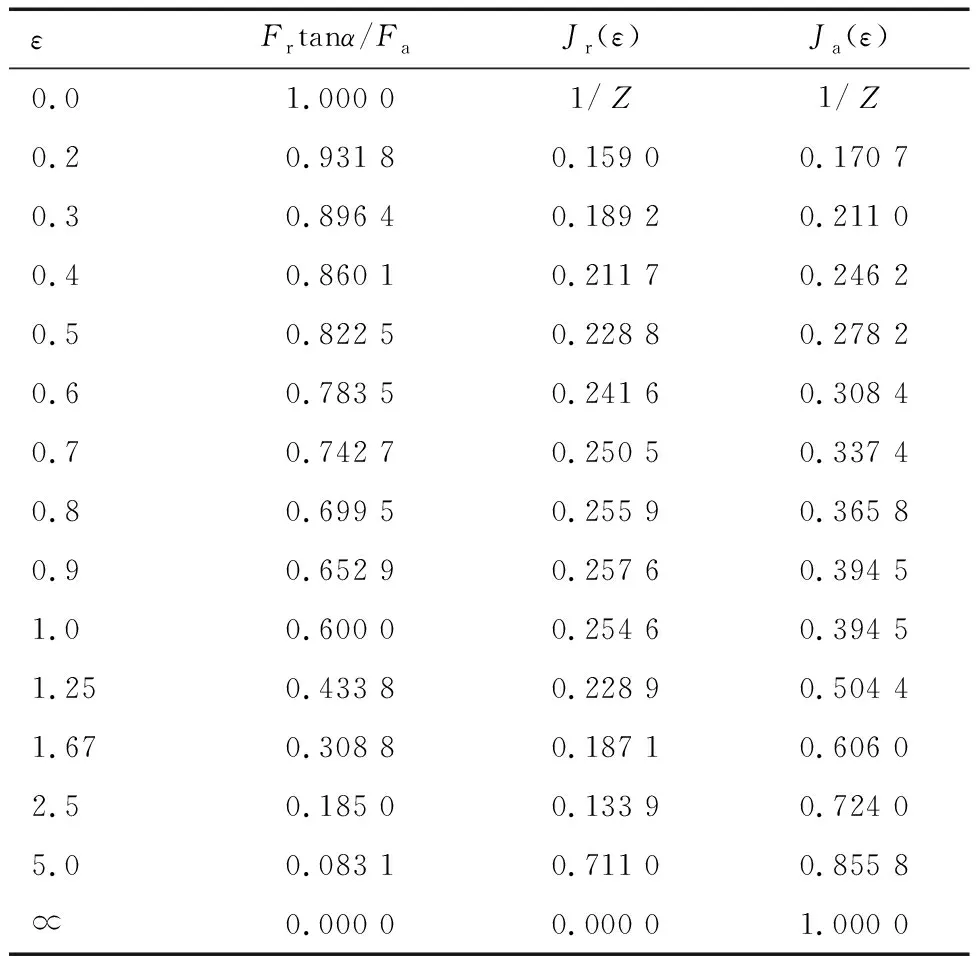
表3 ε、Jr(ε)和Ja(ε)值[8]Tab.3 The value of ε,Jr(ε) and Ja(ε)

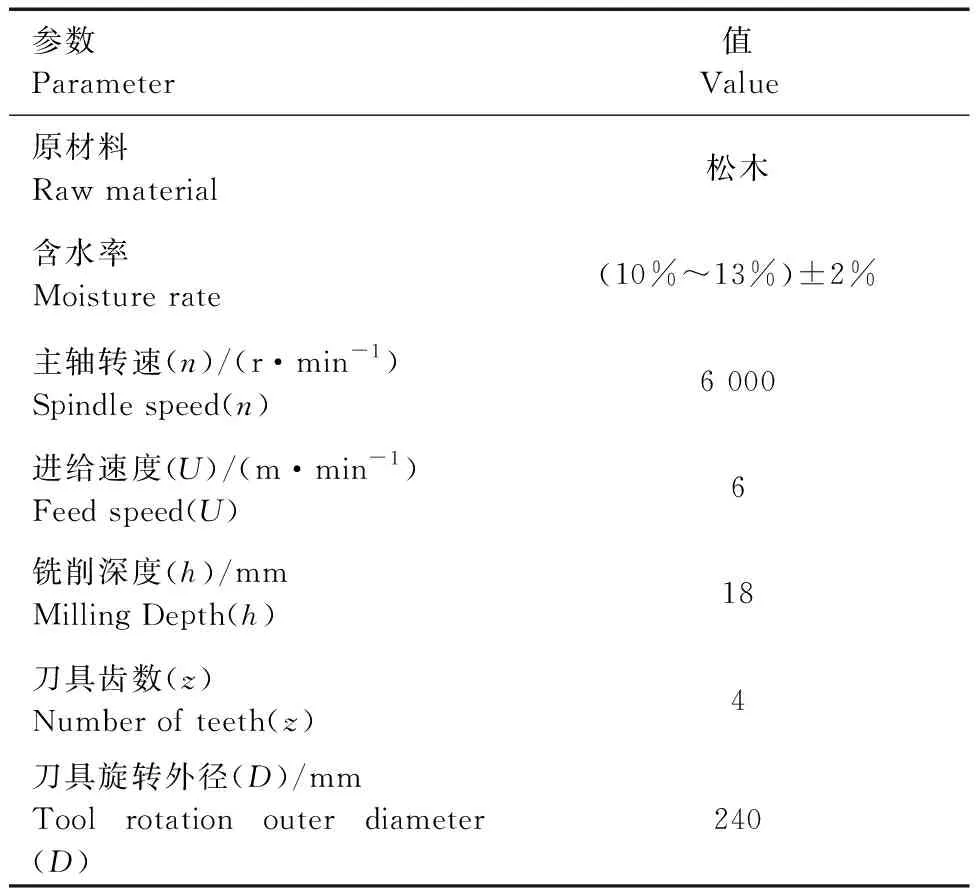
表4 切削力计算条件Tab.4 Cutting force calculation conditions

给定径向载荷Fr=40 N,轴向载荷Fa=80 N,接触角α=25°,计算得到Frtanα/Fa=0.233 1,介于0.308 8～0.185 0,为了得到此时对应的ε、Jr(ε)和Ja(ε),使用拉格朗日线性插值法进行计算,设Frtanα/Fa为x。

(8)

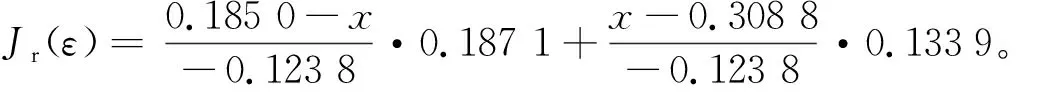
(9)

(10)

将x=0.233 1代入式(8)—式(10)中,分别得到Frtanα/Fa=0.233 1时对应的ε=2.18、Jr(ε)=0.154 6、Ja(ε)=0.678 2。将这3个值及K1和K2代入式(7)得到上轴承径向刚度Jrs=27 596.02 N/mm、下轴承径向刚度Jrx=24 679.37 N/mm。将得到的上下轴承的轴向和径向刚度输入到Adams中,并设置预载荷。

1.4 切削力的计算

切削力是木材切削过程中的主要物理现象之一,是切削木材、切屑和被加工工件表面的木材在刀具作用下发生弹性变形和塑性变形的结果,正确地掌握木材切削力的大小是木工机床设计的必要依据[6]。

切削力的大小对主轴系统造成的影响尤为关键,为正确仿真机床主轴铣削木窗时的状态,需要对切削力进行计算。目前实际应用的切削力和切削功率计算方法有2种,一种为基于理论分析的计算方法;另一种为经验公式计算方法。因为理论计算方法主要是依据断裂力学的概念和计算方法,比较繁琐,牵涉的系数较多,所以在工程计算上多用经验公式,计算切削力和切削功率[9]。本研究使用经验公式(11)完成对切削力的计算,表3中给出切削力的计算条件。所加工产品为IV68系列欧式木窗。

木材切削力的经验公式为

(11)

式中:P为单位切削力,MPa;a为切屑厚度,mm;b为切屑宽度,mm。

单位切削力(P)可按式(12)进行计算[10]

(12)

式中:aw为木材含水率修正系数;q为松木切削的直线斜率;aq为q的修正系数;H为松木切削的直线截距,mm;ah为H的修正系数;Uz为每齿进给量,mm;θ为运动遇角(°)。

查文献[10]得木材含水率修正系数aw=1.0,松木切削的直线斜率q=3.8,q的修正系数aq=1.1,松木切削的直线截距H=0.4,H的修正系数ah=1.45。

每齿进给量(Uz)的计算公式为[11]

(13)

将各已知参数带入计算求得Uz=0.25 mm。

sinθ可用式(14)进行计算。

(14)

式中:h和D均为已知,将其带入后求得sinθ=0.7。

将上述各参数带入式(12)中可求出单位切削力P=125.26 MPa。

切屑厚度a为两相邻切削轨迹间的垂直距离,是一个变化的值,为仿真主轴振动最大的情况,这里取a的最大值amax进行计算。

amax=Uzsinφ0。

(15)

式中:Uz为每齿进给量;φ0为接触角(°)。

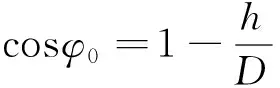
将已知量带入式(15)得amax=0.09。

铣削方式为开式圆柱铣削,切屑宽度b与铣削宽度相等,即b=68 mm。

最终可求得切削力Fx为

将求得的切削力添加到主轴系统多刚体虚拟样机中,并在带轮上添加60 N皮带预紧力,得到最终模型如图4所示,切削力沿坐标系Z轴方向,作用点位于主轴刀具安装部位,皮带预紧力沿-Z轴方向。

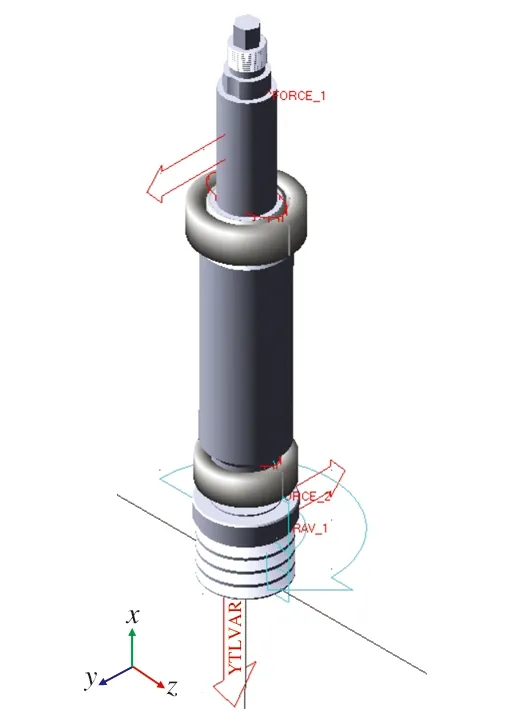
图4 主轴系统多刚体仿真模型Fig.4 Multi-rigid body simulation model of spindle system

1.5 主轴系统刚性体动力学仿真

设置完成所有仿真条件后,进行主轴系统刚性体的动力学仿真,设定仿真持续时间0.04 s,步长0.000 4。仿真后提取主轴质心、切削力作用点和带轮连接点的X、Y、Z向振动曲线,这3点的位置如图5所示,坐标分别为(0,259,0)、(0,439,0)、(0,41,0),所提取的振动曲线如图6—图11所示。

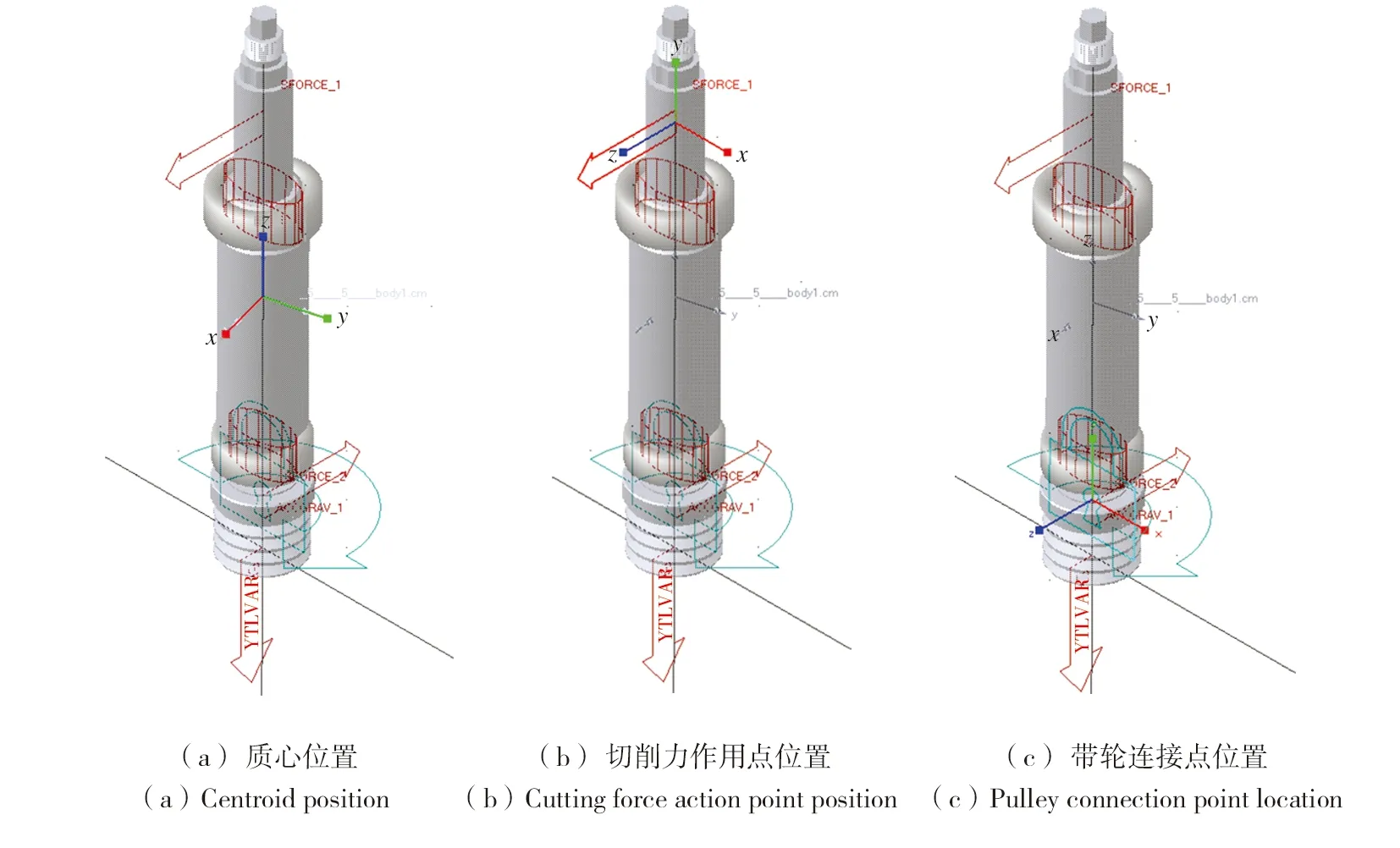
图5 所提取的3点振动曲线位置Fig.5 The position of the extracted three-point vibration curve

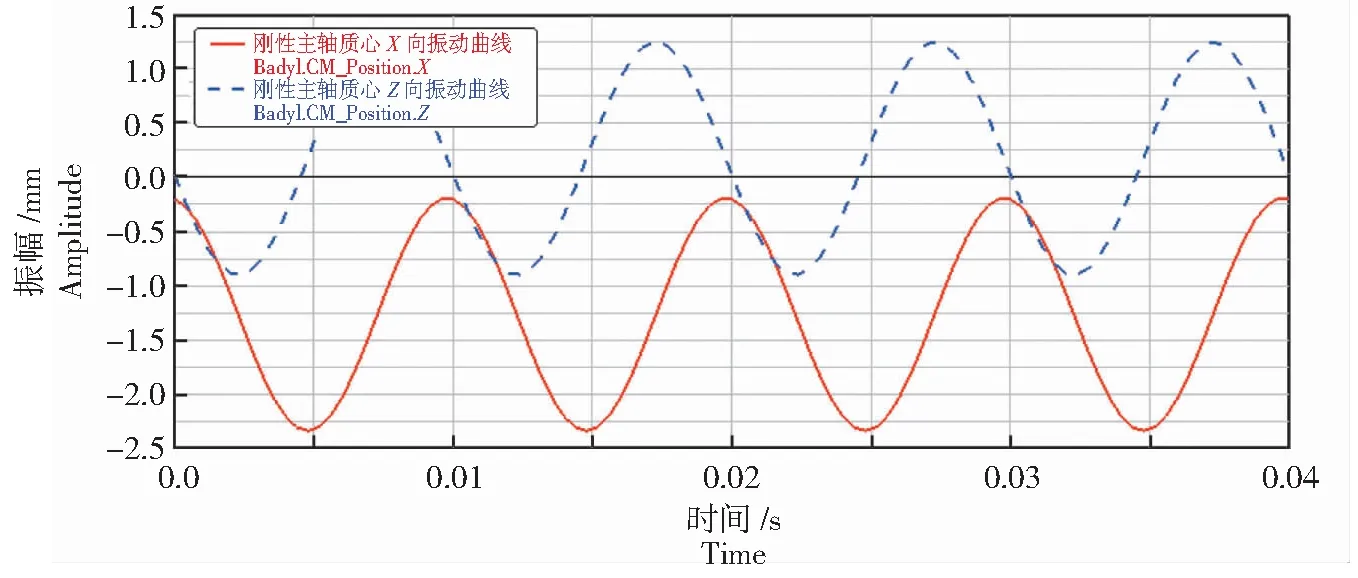
图6 刚性主轴质心X、Z向振动曲线Fig.6 Vibration curve in X and Z directions of rigid spindle centroid

1.6 主轴系统刚性体动力学仿真结果分析

分析图6—图11中的振动曲线可以发现,主轴质心和切削力作用点皆作简谐振动,X、Y、Z向振动曲线皆为余弦或正弦曲线,且周期都为0.01 s。结合图6、图8和图10分析发现,3点的X向振幅分别为1.01 、1.93、6.25×10-4mm;Z向振幅分别为1.08、1.70、6.50×10-4mm,3点的X和Z向振幅几乎一致,3点振幅切削力作用点最大,质心其次,带轮连接点的振幅最小,而且3点的X和Z向的振动曲线并非严格对称于0刻度线,即主轴的回转中心不与Y轴重合,而是向-X和+Z方向偏转一定角度,如图12所示。由图7、图9和图11可知,切削力作用点的Y向振幅最大,为0.01 mm,其次是质心,振幅为0.006 mm,而带轮连接点在Y向上没有振动。

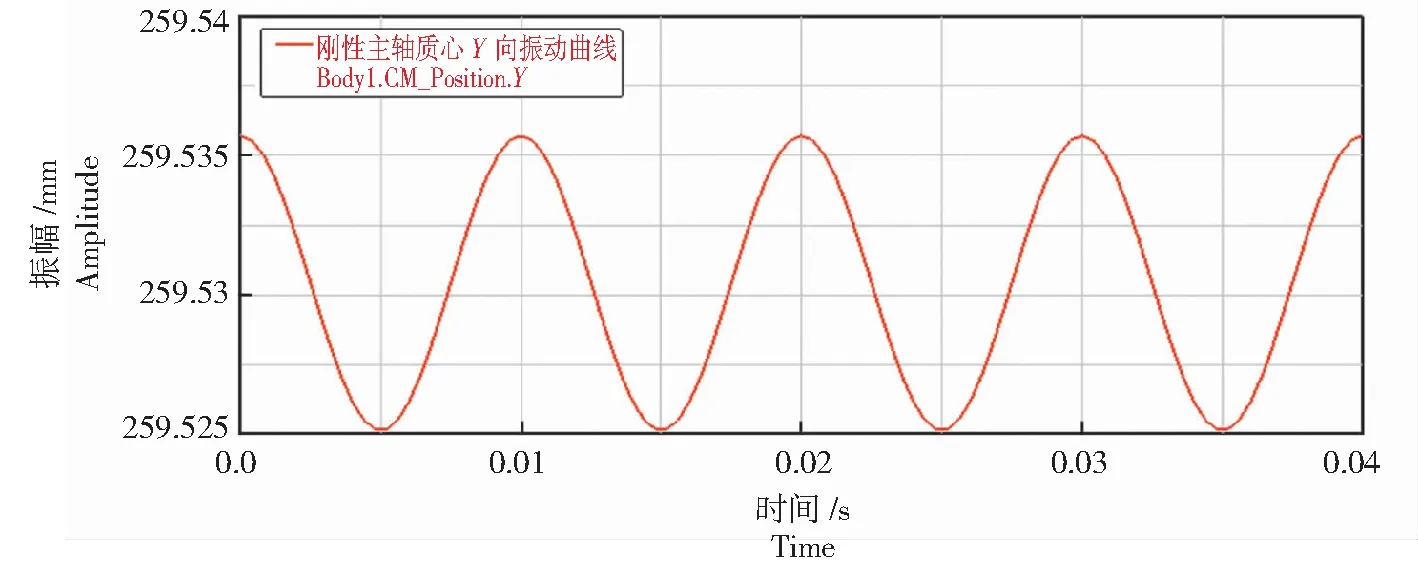
图7 刚性主轴质心Y向振动曲线Fig.7 Vibration curve in Y directions of rigid spindle centroid

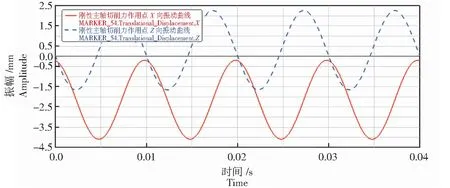
图8 刚性主轴切削力作用点X、Z向振动曲线Fig.8 Vibration curve in X and Z directions of rigid spindle cutting force action point

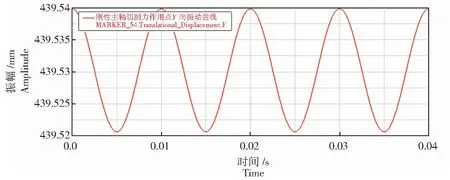
图9 刚性主轴切削力作用点Y向振动曲线Fig.9 Vibration curve in Y directions of rigid spindle cutting force acting point

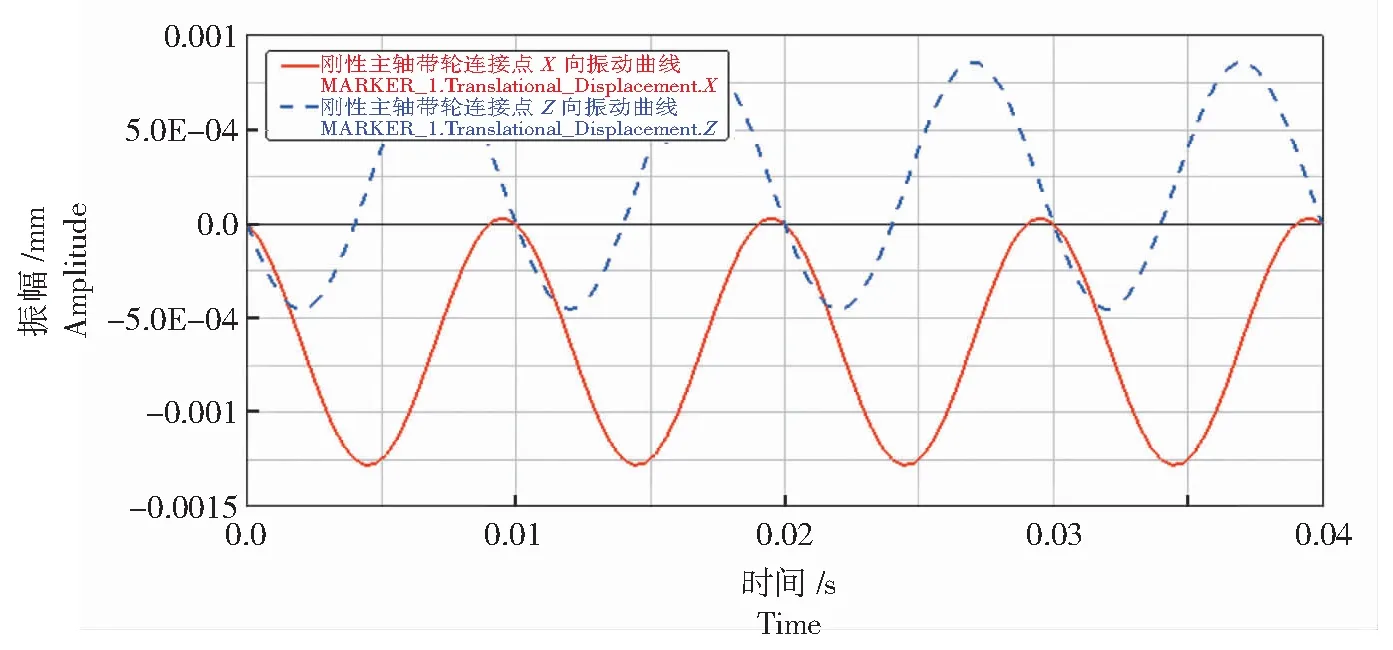
图10 刚性主轴带轮连接点X、Z向振动曲线Fig.10 Vibration curve in X and Z directions of rigid spindle pulley connection point

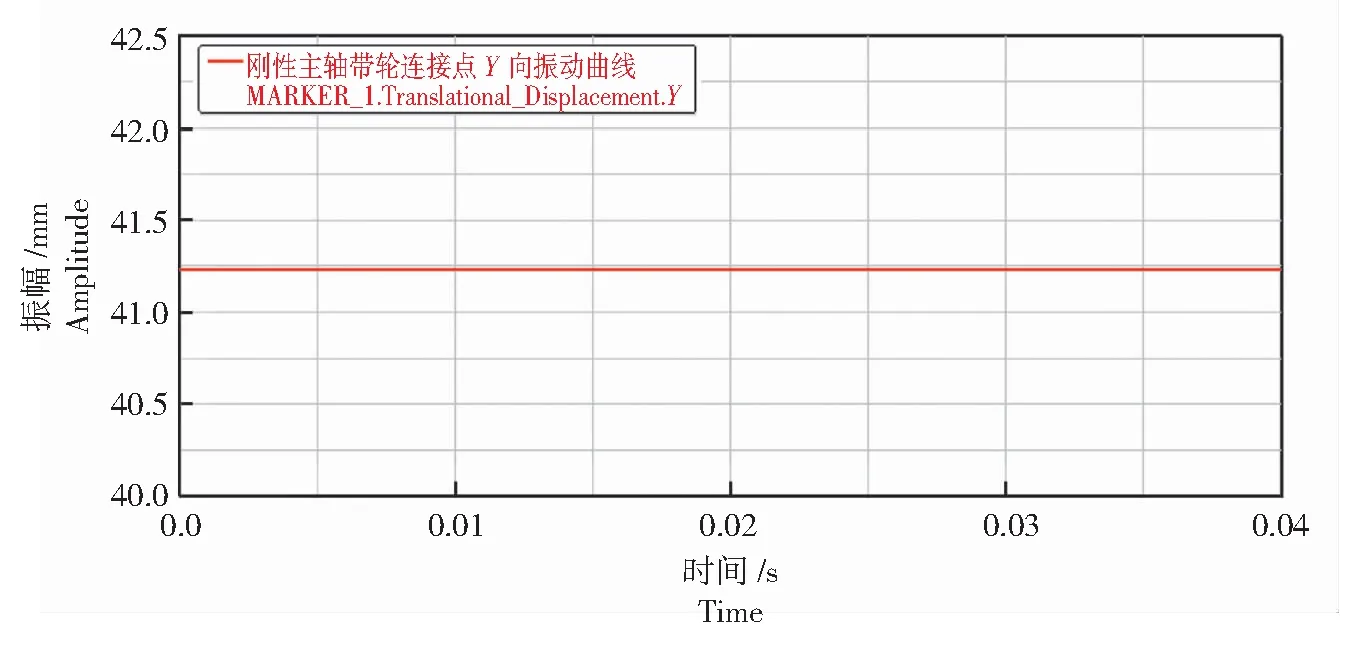
图11 刚性主轴带轮连接点Y向振动曲线Fig.11 Vibration curve in Y directions of rigid spindle pulley connection point

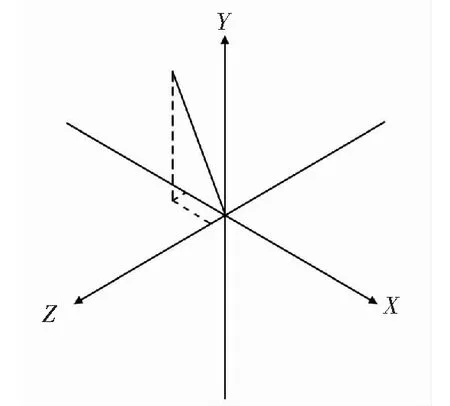
图12 偏移的主轴回转中心Fig.12 Offset spindle center of rotation

2 刚柔耦合模型的建立与仿真

2.1 刚柔耦合模型的建立

把模型当作刚性系统来处理,没考虑构件的变形,在精度要求较高时,可能出现仿真与实践不符的情况[6]。主轴系统对精度要求较高,为能准确研究主轴系统的动力学特性,不能忽略在实际工作过程中的微小振动与变形,将主轴设为柔性体能使仿真结果更加接近实际情况。

Adams中柔性体的载体是包含构建模态信息的模态中性文件(Modal Neutral File,MNF),因此柔性体的创建必须借助功能强大的有限元软件来完成[12]。借助有限元软件Ansys可以完成对柔性主轴的创建。

基本步骤[13-18]:

1)将主轴三维模型导入Ansys。

2)设置单元类型为Solid(Brick8node185),设置材料属性。

3)分别在上下轴承支承部位及带轮连接部位中心创建连接点。

4)划分单元,划分单元后主轴如图13所示。

图13 划分单元后的主轴Fig.13 Main axis after dividing the unit

将上下轴承支承部位及带轮连接部位设置为刚性区域,如图14所示。使用Adams接口输出模态中性文件。将主轴模态中性文件导入Adams的模型中替换原有刚性主轴。

图14 主轴模型刚性区域Fig.14 Spindle model rigid area

替换完成后得到的主轴系统的刚柔耦合模型如图15所示,其中主轴为柔性体,带轮为刚性体。

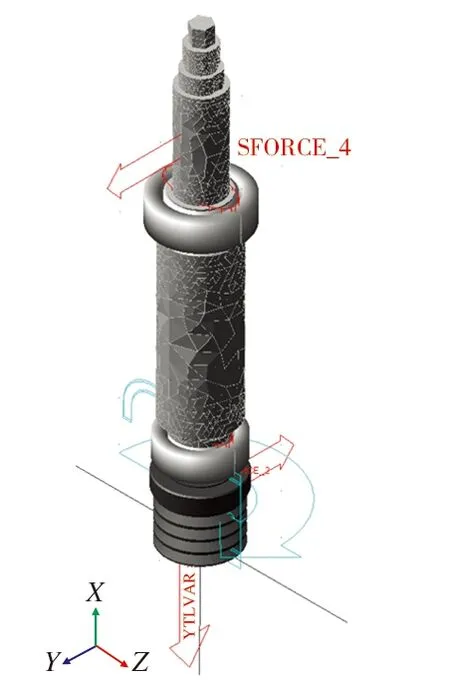
图15 主轴系统刚柔耦合模型Fig.15 Rigid-flexible coupling model of spindle system

2.2 主轴系统刚柔耦合模型仿真

设置仿真条件与进行刚性体仿真时一致。进行仿真后得到图16—图21所示结果。

由于带轮连接点的X、Z向振动曲线的起点坐标差较大,为方便分析将2条振动曲线的起点与坐标原点重合。

2.3 主轴系统刚柔耦合模型仿真结果分析

由图16—图21可以看出,柔性主轴质心、切削力作用点和带轮连接点的X向和Z向振动曲线与主轴为刚性时的情况存在较大差异,虽然振动曲线周期同样为0.01 s的正弦或余弦曲线,但是各点的三向振幅发生了较大的变化。主轴质心、切削力作用点和带轮连接点的X向振幅分别为:2.9×10-3、0.01、6.5×10-4mm;3点的Z向振幅与X向振幅一致,分别为:2.9×10-3、0.01、6.5×10-4mm。而且可以看到3点的振动起点较主轴为刚性时发生了变动,但并不影响对3点振幅的分析。分析图17、图19和图21,3点Y向振动曲线周期同样为0.01 s,振幅分别为4.5×10-4、2.0×10-4、5×10-5mm。

图17 柔性主轴质心Y向振动曲线Fig.17 Vibration curve in Y directions of the flexible spindle centroid

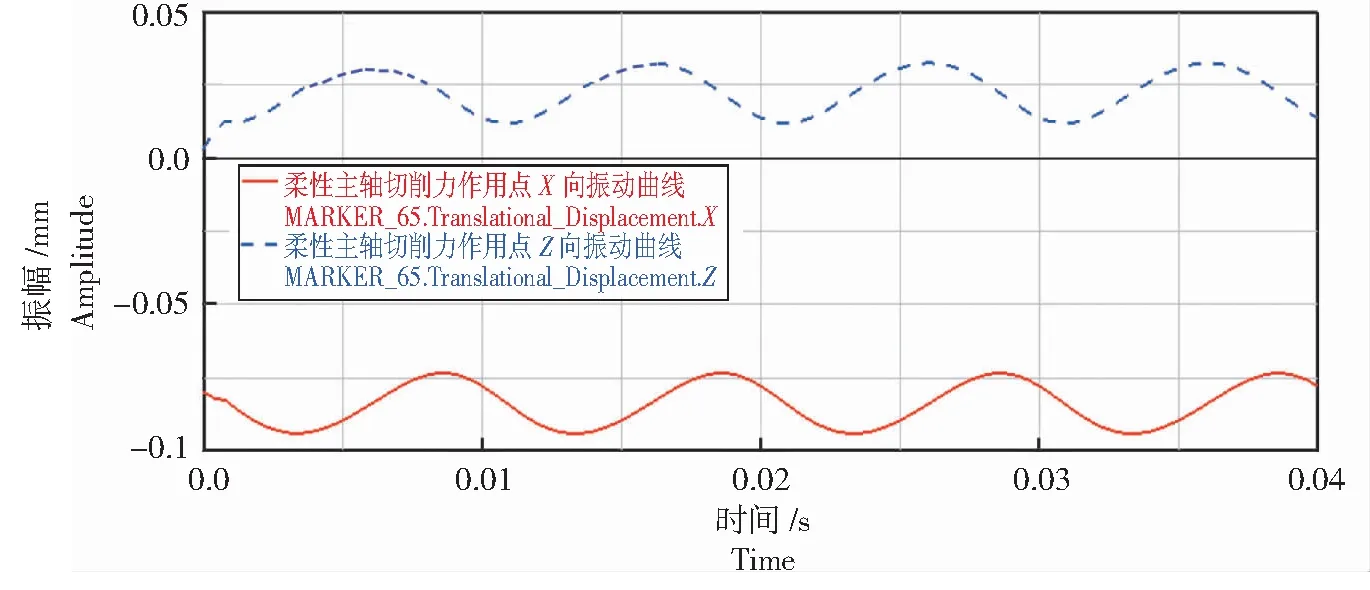
图18 柔性主轴切削力作用点X、Z向振动曲线Fig.18 Vibration curve in X and Z directions of flexible spindle cutting force action point

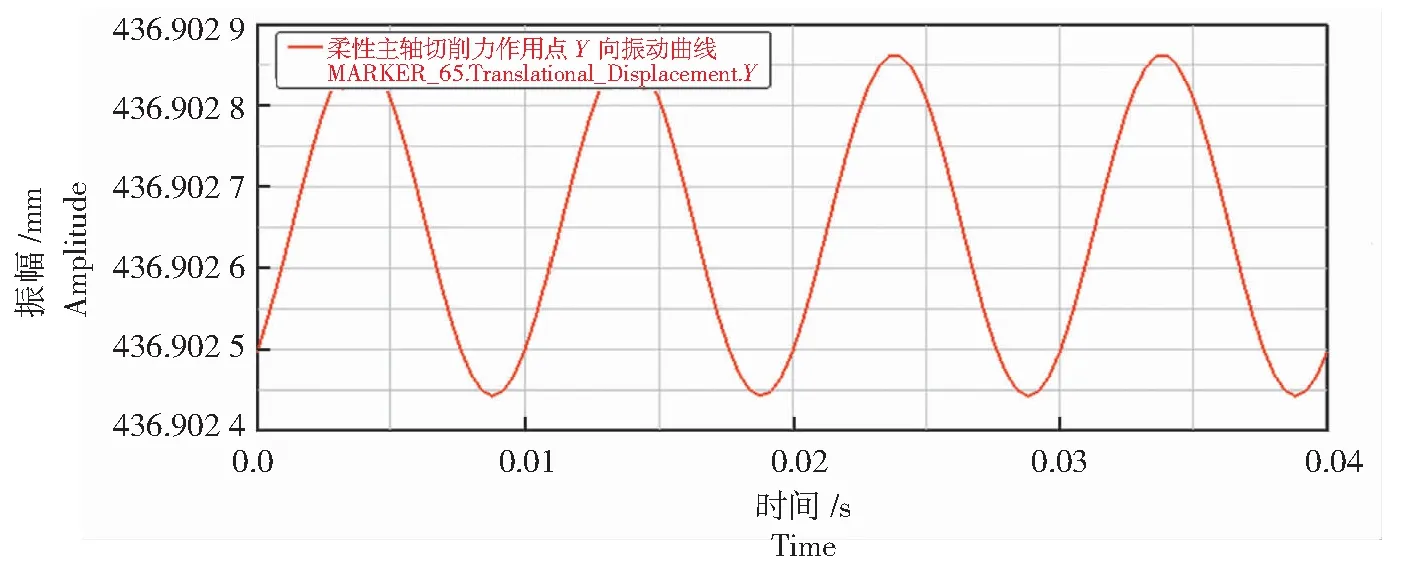
图19 柔性主轴切削力作用点Y向振动曲线Fig.19 Vibration curve in Y directions of flexible spindle cutting force action point

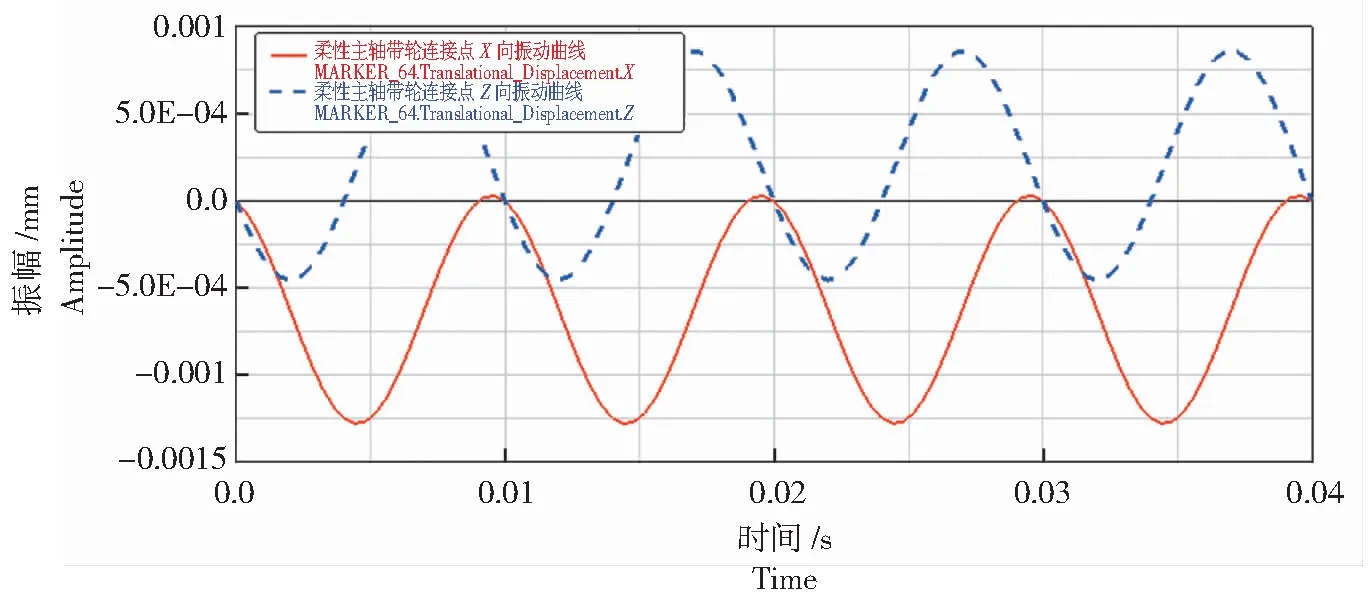
图20 柔性主轴带轮连接点X、Z向振动曲线Fig.20 Vibration curve in X and Z directions of flexible spindle pulley connection point

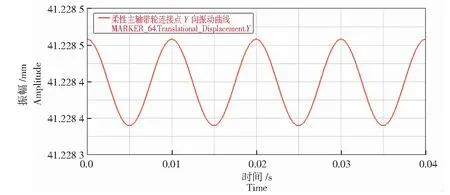
图21 柔性主轴带轮连接点Y向振动曲线Fig.21 Vibration curve in Y directions of flexible spindle pulley connection point

3 仿真结果比较

比较主轴为刚性和柔性2种情况时的振动曲线,发现这2种情况下3点的振动曲线周期皆为0.01 s。表5中列出了主轴为刚性和柔性时,主轴质心、切削力作用点和带轮连接点的X、Y、Z向振幅。

表5 刚、柔主轴3点振幅Tab.5 Three-point amplitude of rigid and flexible spindles mm

由表5可以发现,当主轴为柔性体时质心和切削力作用点的振幅远远小于主轴为刚性时,从主轴0.01 mm的检验标准来看,刚性主轴的仿真结果是不准确的,而柔性主轴的仿真结果更加符合实际情况。无论是刚性主轴还是柔性主轴,切削力作用点的X、Z向振幅由于受到切削力的作用,所产生的振幅是3点中最大的,其次是质心,带轮连接点的振幅最小。而在3点的三向振动中,Y向振幅是最小的,若以柔性主轴的Y向振幅为准,则这个振幅很微小,对木窗的加工精度几乎没有影响,因此在主轴结构改进时可不做考虑。切削力作用点即铣刀装配位置的振动对木窗加工质量影响最大,应从如何减小切削力作用点的振幅入手来进行主轴结构的优化。

4 结论

1)提取了主轴为刚性体和柔性体时的主轴质心、切削力作用点和带轮连接点的X、Y、Z向振幅。

2)对比主轴为刚性体和柔性体2种情况时的仿真结果,发现主轴为柔性体时振动规律更加符合实际情况。

3)以刚柔耦合模型的仿真结果为准,切削力作用点、质心和带轮连接点的X、Z向振幅依次从大到小,而Y向振幅很微小可忽略不计,如何减少切削力作用点的振幅是主轴改进的重点,本研究中的刚柔耦合模型动力学仿真结果为主轴系统结构的改善提供了参考依据。