基于改进飞蛾扑火算法的电动汽车充电站选址

李宏玉,张孝民,姜晨辉,彭康,宋来鑫 ,李桐壮

(东北石油大学 电气信息工程学院,黑龙江 大庆 163318)

0 引 言

近年来,我国电动汽车的使用数量迅速增长,电动汽车充电站是电动汽车数量增长的基础保障,但是仍面临技术落后等诸多问题。因此,降低充电站建设成本,降低用户使用成本,对电动汽车充电站的位置进行有效规划,是目前急需解决的问题。

本文利用Tent映射和反向学习策略提高飞蛾扑火算法(moth-flame optimization, MFO)初始种群的多样性。引入动态惯性权重策略,在前期增加搜索能力,在后期提高解的收敛速度,得到混沌反向学习的飞蛾扑火算法(Tent opposite ameliorative moth-flame optimization, TOAMFO)。并对以全社会总和成本最小为目标的选址模型进行求解。

1 充电站选址模型

电动汽车充电站的规划既要考虑运营商的成本和收益问题,又要考虑用户的使用成本等方面的因素。本文采用以建设成本、年运行维护成本、用户前往充电站耗时成本和用户等待成本为目标的电动汽车充电站选址模型［1］14。

1.1 目标函数

建设成本主要包括充电桩、土地、电缆和变压器等费用,如式(1)所示。

(1)

式中:i为需求点;j为候选站;yj为决策变量,去该候选站为1,不去为0;O为固定成本;β为充电桩单价;μ为充电桩等设备的等效投资系数;Nj为候选站j的充电桩数量;n为充电站使用年限;r0为贴现率。

年运行维护成本由人力成本和维护成本组成,如式(2)所示。

(2)

式中:α为折算系数。

用户前往充电站成本,如式(3)所示。

(3)

式中:cij为式中单位耗时成本;qi为需求点的需求数量;dij为需求点到候选站的距离;τ为拥堵系数;V为电动汽车平均行驶速度。

用户等待成本如下所示。

(4)

(5)

(6)

(7)

式中:tj为等待时间;ρj为充电桩服务强度;λ为平均每小时到达充电站的电动汽车数量;ε为充电桩单位时间服务数量;P0为充电站空闲概率;T为最大等待时间;W为等待成本。

社会总成本如式(8)所示

MinF=C1+C2+C3+C4

(8)

1.2 约束条件

约束条件如式(9)所示。

Nmin≤Nj≤Nmax

(9)

式中:Nmin、Nmax分别为充电站内充电桩的最小和最大值。

(10)

式(10)中需求点只能选择唯一的充电站。

2 改进飞蛾扑火算法及流程

2.1 改进飞蛾扑火算法

2.1.1 Tent混沌映射

目前Logistic映射使用率较高,但是该映射在不同区域内取值率有所不同［2］。导致Logistic映射对算法的收敛速度造成一定的影响,Tent映射相较于Logistic映射性能更优越,产生的初始值更加均匀［3］。当u=1/2时,是Tent映射最常用的参数。

2.1.2 反向学习

OX为种群的反向解,将种群X和种群反向解OX合并得到新种群［4］,然后计算出新种群的适应度值,并按照从小到大的顺序进行排列选择前N个作为飞蛾扑火算法的初始种群［5］。

2.1.3 动态惯性权重策略

引入动态惯性权重策略,在迭代初期,惯性权重因子较大,全局探索能力强,可以增强搜索性能,避免陷入局部最优解。在迭代后期,惯性权重因子减小,将大大加快迭代次数。T为最大迭代次数,ω为动态惯性权重［6］,如式(11)所示。

(11)

图1为动态惯性权值变化曲线。

改进后的位置更新公式［7］如式(12)所示。

S(Mi,Fj)=ω×Di×ebt×cos(2πt)+(1-ω)Fj

(12)

2.2 算法流程

步骤一:设置初始化算法参数,飞蛾数量为n、维数为d和最大迭代次数T等。

步骤二:种群Tent初始化,产生种群个体。

步骤三:将种群个体利用反向学习,产生反向解,求出飞蛾适应度值,按照适应度值进行排序,选取较优适应度值组成初始种群。

步骤四:更新火焰数量。

步骤五:调整种群,防止超出边界。

步骤六:适应度值排序。

步骤七:按式(11)更新动态惯性权值。

步骤八:按式(12)更新飞蛾位置。

步骤九:若满足终止条件,算法结束,获得最优解,否则返回步骤四。

3 算例研究

以某市典型新区的电动汽车充电站选址定容为例进行分析,在一个平面区域［0,50］×［0,50］内设计了一个有15个需求点和5个备选站点的测试实例［1］17,如表1所示。表1列出了需求点和候选站的坐标。每座充电站的固定成本为210万元,每个充电桩的价格为10万元,充电桩等效投资系数为2万元/台,充电站折旧年限为20年,贴现率为0.08［8］。

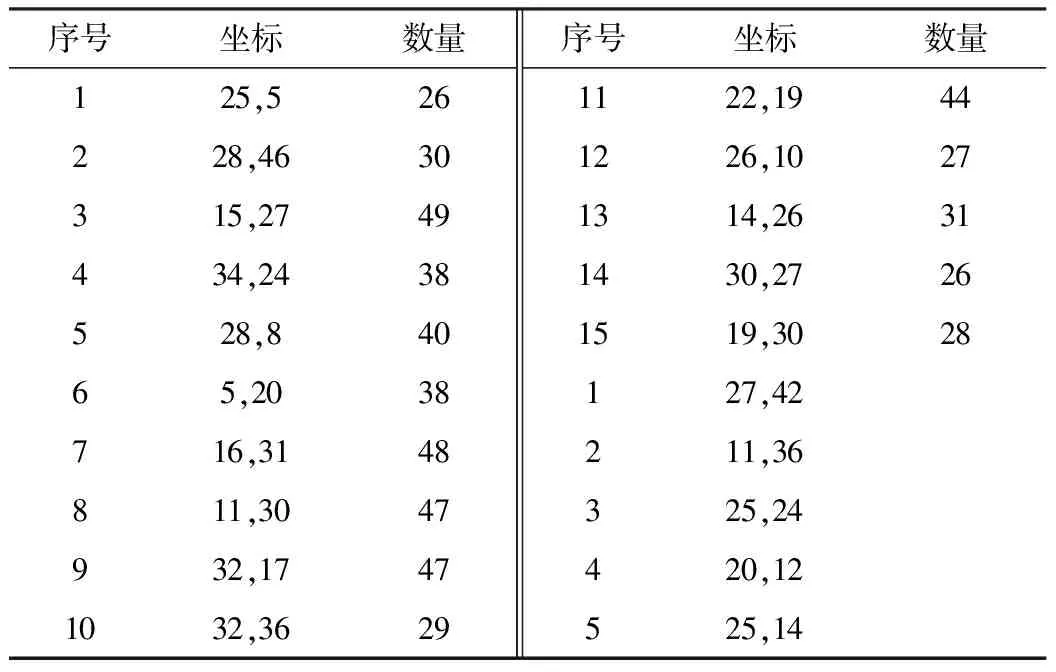
表1 需求点和候选站的坐标

人力成本和维护成本的折算系数为0.1。前往充电站的耗时成本为35 元/h,路途曲折系数为1.8,车辆平均行驶速度为15 km/h,拟建设充电站最大为3座。站内充电桩的最小数量为4台,站内允许安装充电桩的最大数量为20台。每个充电桩每小时服务两台电动汽车,等待成本为60 元/h。

图2为TOAMFO算法的选址方案,根据社会总成本最小为目标函数,所选候选站为1、3、5。

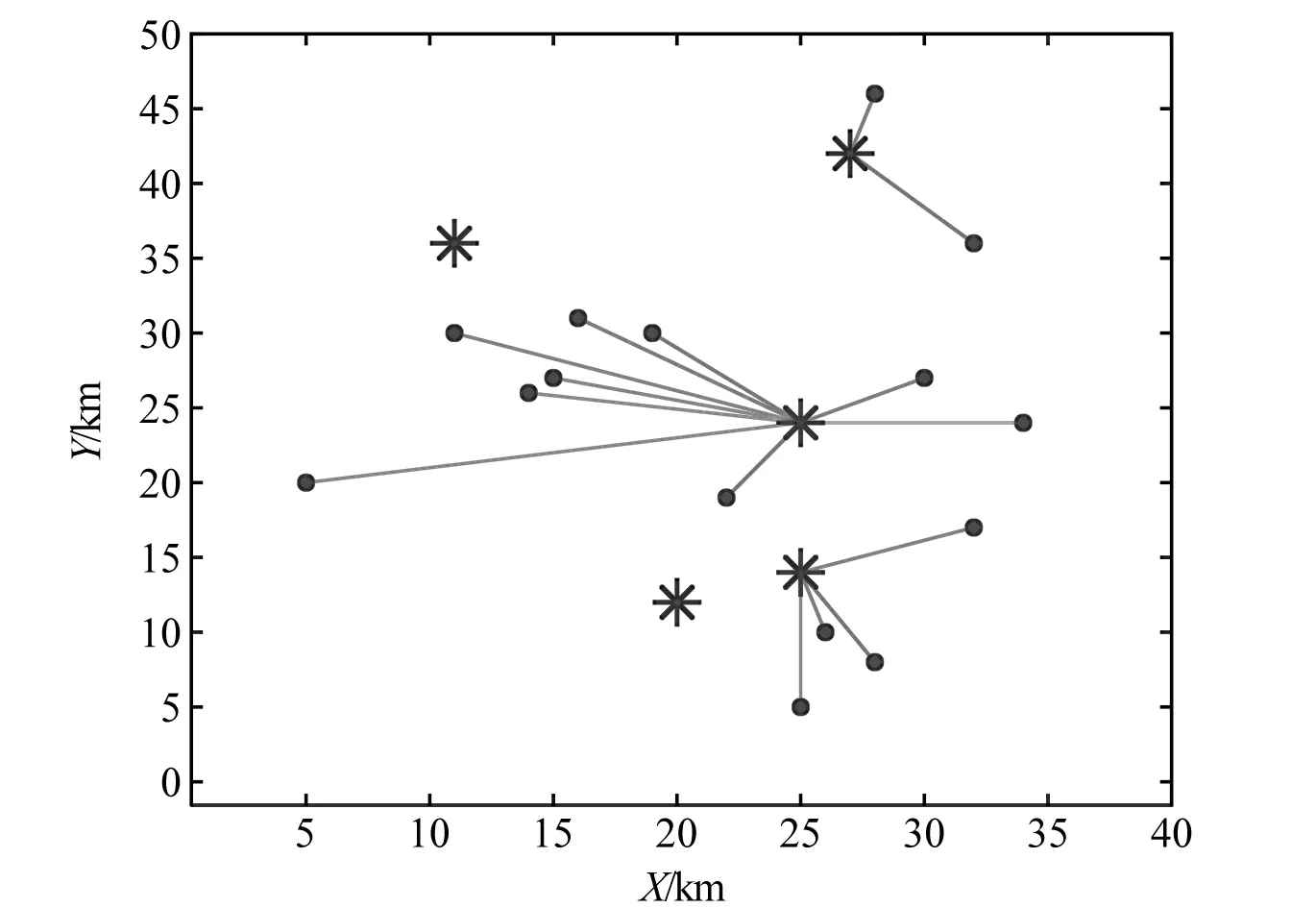
图2 TOAMFO选址图

TOAMFO、MFO和粒子群优化算法(particle swarm optimization, PSO)三种算法的选址方案对比图如图3所示。由图3可知,TOAMFO的选址方案社会总成本最小,为9 368 247元,证明该算法具有优越性。

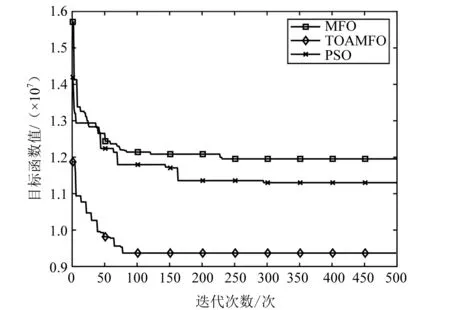
图3 三种算法对比图

4 结束语

本文针对电动汽车选址问题,提出一种新型的改进飞蛾火焰算法。利用改进算法对模型进行求解,将改进算法与MFO和PSO进行比较,可以明显得出加入了初始化策略和动态惯性权重策略的改进算法在速度和精度上具有优越性,避免算法陷入局部最优,提升全局寻优能力。结果表明,本文提出的改进飞蛾扑火算法可以得到合理的选址方案。后续研究可以将网损成本纳入目标函数中,将研究进一步完善。