结合图卷积的在线编程系统成绩预测模型
罗文劼,肖梓良
(河北大学 网络空间安全与计算机学院,河北 保定 071002)
0 引 言
随着在线教育的快速普及,各种在线编程系统(programming online judge,POJ)被广泛应用于计算机科学教育的辅助教学和编程竞赛的辅助培训中[1]。在辅助教学中,教师借助POJ培训并掌握学生的编程水平[2],通常的交互顺序如下:
(1)教师从POJ题库中选择要布置的题目,发布为题目集。
(2)学生接收题目集,编写题目解决方案的源代码并提交。
(3)POJ将代码编译成可执行文件,将输出结果与标准答案进行比较。
(4)POJ反馈学生该方案是否正确。如果不正确,则提示错误,并允许学生对该题目再次解答。
(5)教师根据POJ提供的答题信息了解学生编程水平。
计算机科学考验学生的抽象思维和实践能力,许多学校相关课程期末不及格率超过30%[3],一种解决方法是通过学生早期POJ测试的表现预测成绩,对学生进行针对性辅导,也推进下游任务进行[4-6]。
POJ允许学生多次解答,因此存在提交记录、重复提交次数、最终成绩等特征。现有模型往往只利用最终成绩特征,并需要大量的学生背景信息,对数据源要求较高[7-9]。也有模型利用了在线学习的特征[10-12],但仅利用了进行了POJ测试且存在期末成绩的有标签学生的信息,未有效利用没有期末成绩的无标签学生的信息。
为解决以上问题,本文提出一种结合图卷积的在线编程系统成绩预测模型DKT-GCN。通过改进深度知识追踪模型(deep knowledge tracing,DKT)对学生提交记录建模获取知识状态,然后结合图卷积模型在POJ测试成绩的基础上嵌入知识状态信息,利用融合后特征预测学生成绩等级。该模型保留无标签学生信息提升预测效果,教师可以根据模型的预测获得学生的成绩等级与知识状态,以此设计个性化教育策略,对不同的学生进行个性化辅导,帮助学生更好地提高成绩。
1 相关工作
1.1 深度知识追踪模型
学生在给定的学习过程中解决相关问题,解决结果的时间序列为x0,x1,…,xt, 知识追踪模型目的在于预测学生在下一个时间步上的解决结果xt+1。 深度知识追踪模型是利用循环神经网络建模学生知识状态,避免了大量的特征标注,取得了最好的预测效果[13]。
近年来研究人员针对不同场景对DKT模型加以改进与应用,通过重构损失函数提高模型的稳定性[14],利用学生的学习轨迹预测在下一次编程问题上的成功几率[15],结合协同过滤算法进行题目推荐[16]。
1.2 图卷积模型
传统的卷积神经网络通过固定大小的卷积核抽取特征,难以直接应用于不规则空间结构数据。为此Kipf等提出适用于不规则图结构数据的图卷积神经网络(graph convolutional network,GCN)并应用于结点的半监督分类任务[17]。GCN可以较好融合图中的结点信息和结构信息,已被广泛应用于推荐系统[18]、交通预测[19]和文本分类[20]等场景。
在线教育领域中,每个课程的前置课程数量不同,Hu等利用GCN将前置课程知识对目标课程的重要性加权进行成绩预测[21]。交互式题库中每个学生的题目交互不同,Li等利用GCN处理学生与题目的关系,并在隐含层之间增加残差连接解决过平滑问题[22]。
本文参考以上模型处理不规则数据的思路,利用GCN处理不规则的学生相似关系,利用半监督特点挖掘无标签学生的信息,将更多信息融入模型。
2 结合图卷积的在线编程系统成绩预测模型
针对POJ教学中成绩预测模型的不足,本文提出一种结合深度知识追踪与图卷积的在线编程系统成绩预测模型DKT-GCN,模型总体结构如图1所示,具体流程如下:
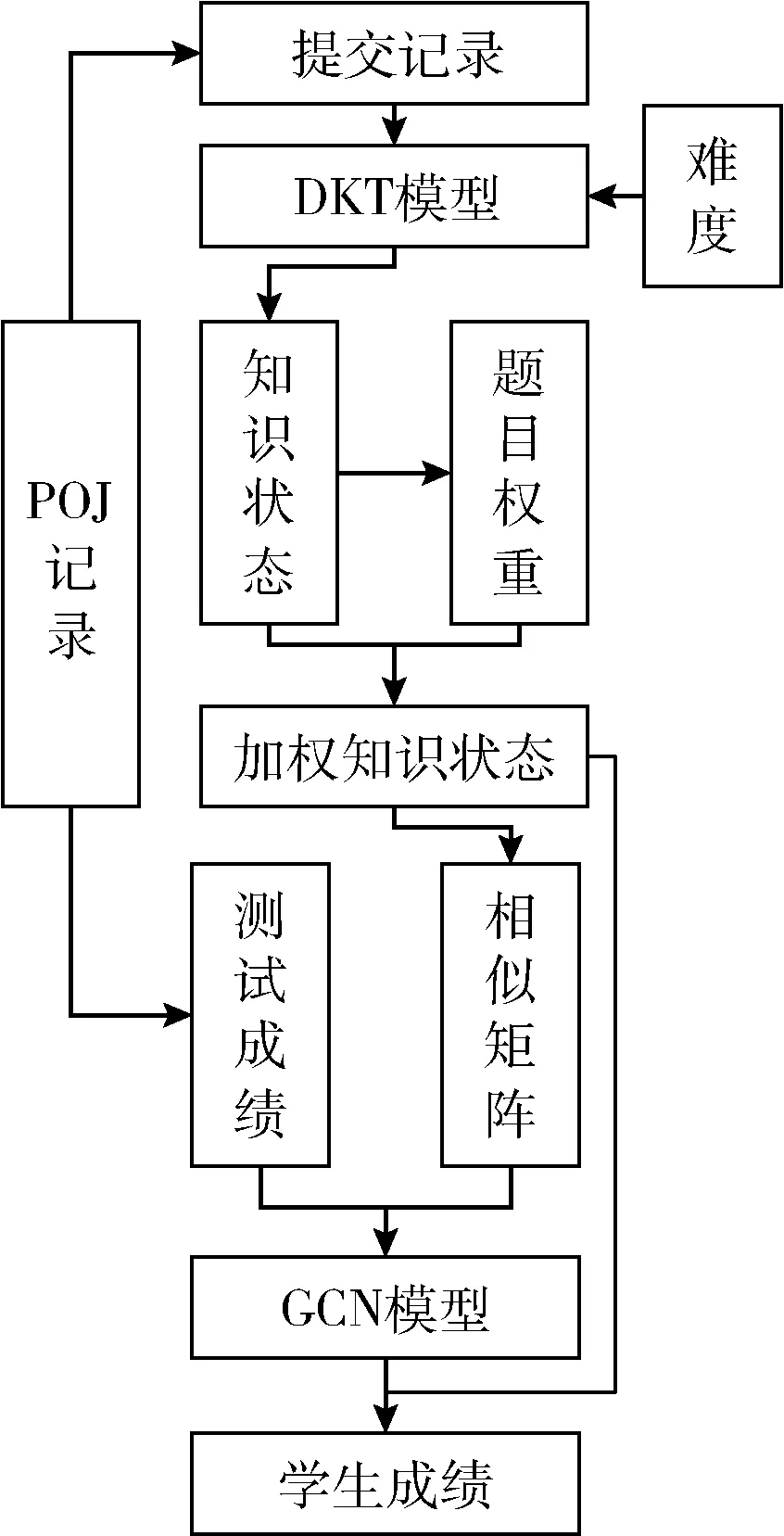
图1 DKT-GCN模型结构
(1)通过POJ题目的提交次数与正确解答次数计算题目正答率,并转化为题目难度特征。
(2)将难度与学生提交记录进行独热编码,改进DKT模型输入,训练模型获取学生知识状态向量。
(3)使用熵权法挖掘不同知识对学生成绩的影响,获取学生的相似度矩阵。
(4)结合POJ测试成绩构建GCN预测网络,融合多层特征预测学生期末成绩。
2.1 学生相似度矩阵
2.1.1 学生知识状态向量
本文尝试利用GCN挖掘无标签学生的信息,因此通过DKT模型建模学生知识状态,构建全体学生相似关系。设POJ测试中共有M个学生,N个题目。原始DKT模型输入考虑当前时刻提交的编程题目编号和学生解答结果,输出学生答对相关题目的概率。但是原始DKT模型认为每个题目是等价的,忽略了题目本身的特征。题目的难度特征对解答状况有较强的影响,例如高难度的题目学生答对的概率更低,所以引入题目难度信息有助于模型训练。因此本文将题目的难度特征引入提交记录,改进DKT模型的输入。引入难度特征后模型结构如图2所示,dt是学生在t时刻提交题目的难度特征,xt是学生提交记录的独热编码,ht是模型的隐含层状态,kst是模型输出的学生知识状态。
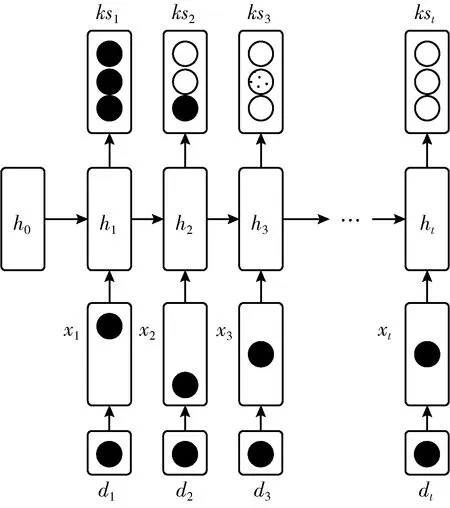
图2 引入难度的深度知识追踪模型
在POJ场景下,题目一旦被提交到题库,系统就会统计所有解答过该题目学生的答题情况。难度被映射为题目的正答率,即题目统计中正确解答次数与提交次数的比值。题目难度越小,学生在越少的提交次数内正确解答;难度越大,学生在越多的提交次数内正确解答或者错误解答。具体来说,首先通过式(1)计算题目n的正答率acrn,n∈N
(1)
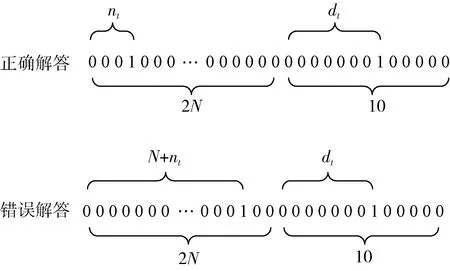
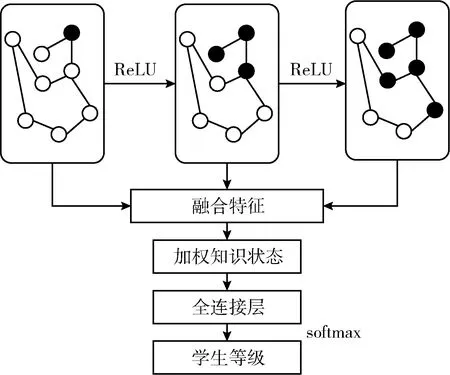
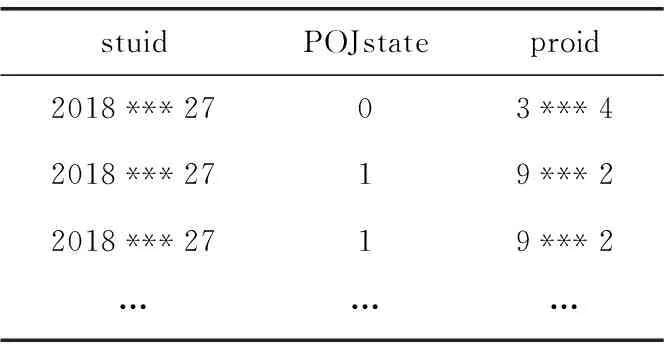
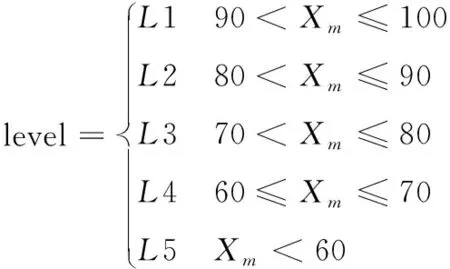
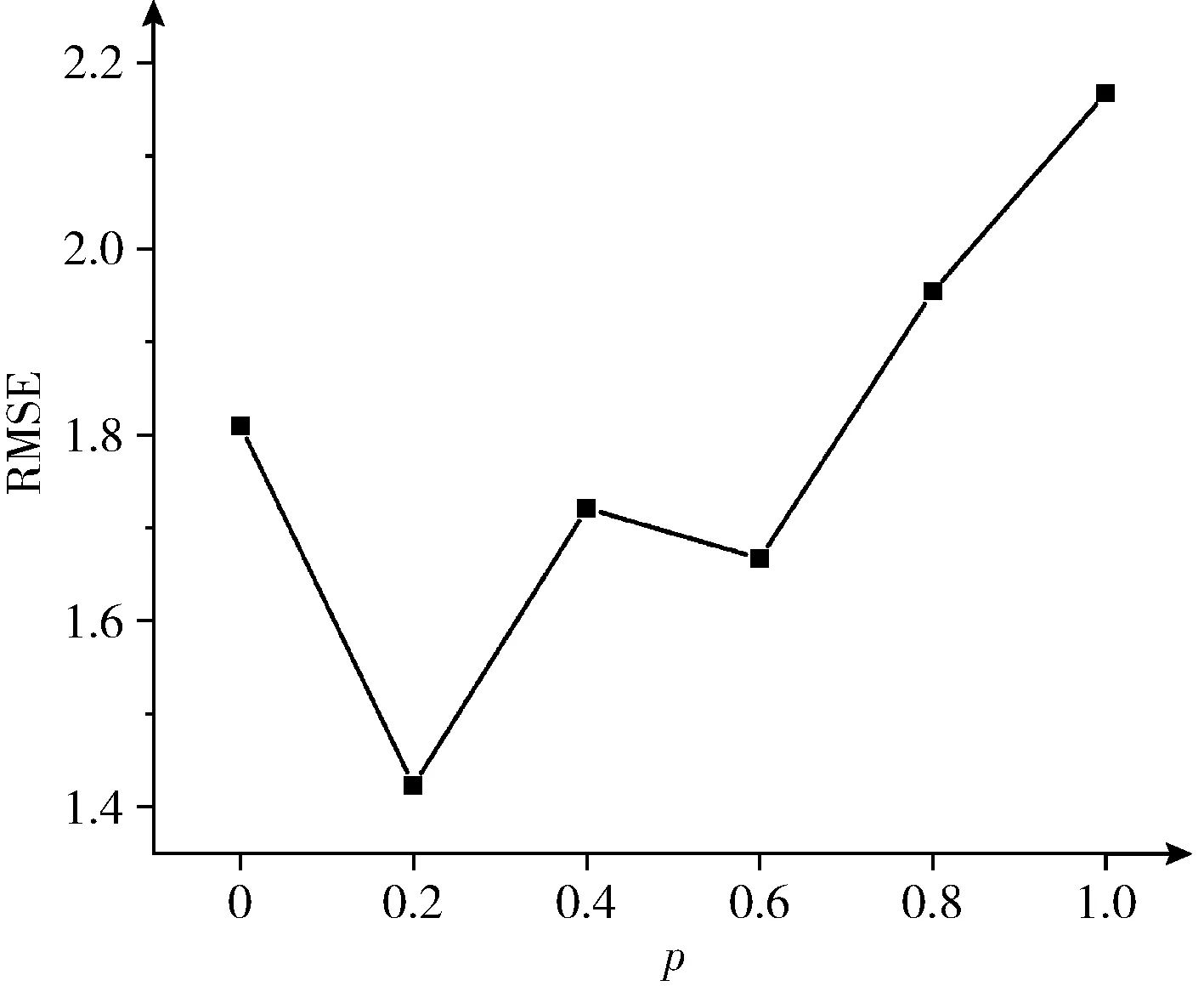
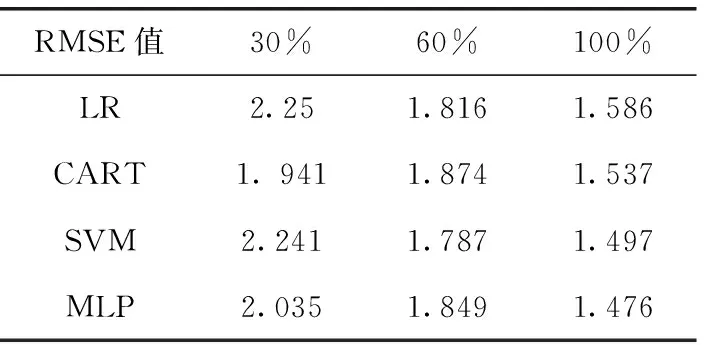
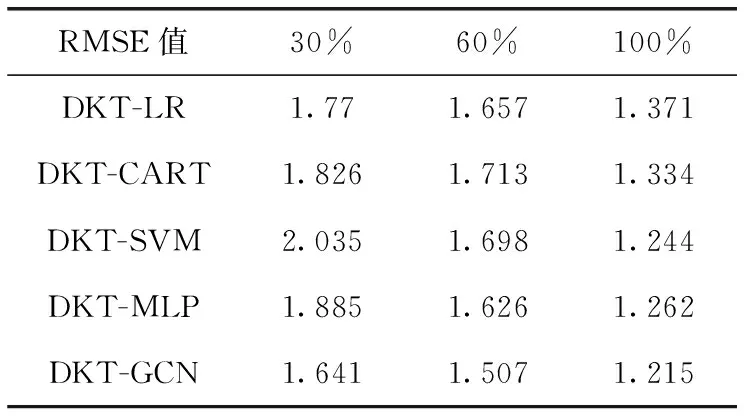
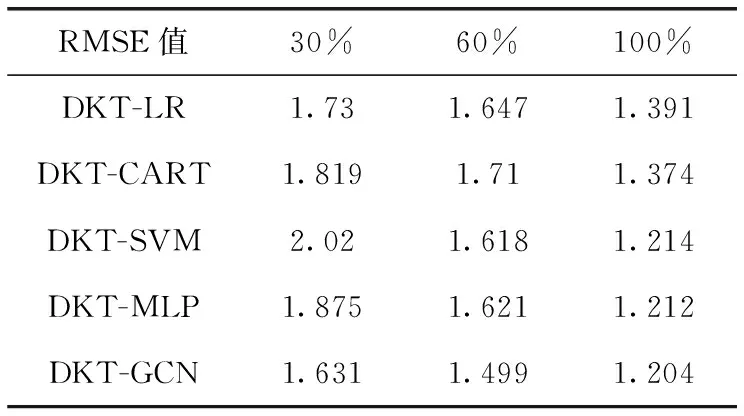
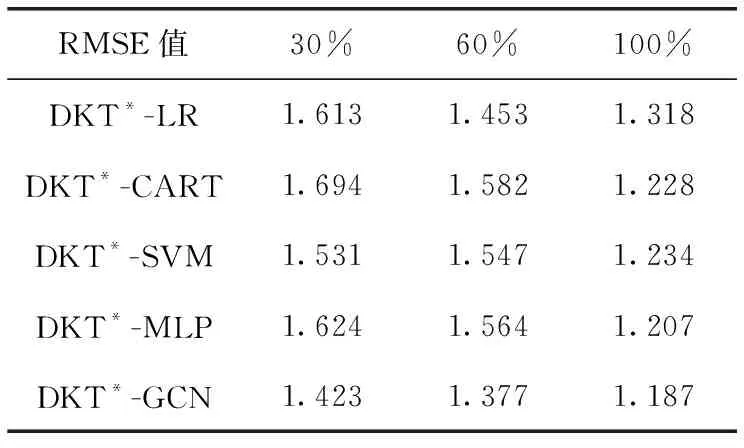
式中:ACCn是题目n统计中POJ反馈为正确解答的提交次数的总数;SUBn是题目n统计中的提交次数的总数,无论POJ反馈为正确解答还是错误解答。所有题目至少有一次正确解答记录,因此0 之后对正答率acrn进行等宽离散化处理,划分成固定个数且宽度相同的区间。结合常用的难度划分方法,如式(2)将题目正答率acrn划分为十级难度,获取难度特征d(n),1≤d(n)≤10 (2) 最后使用独热编码将题目的难度融入学生提交记录。学生在t时刻提交题目的编号表示为nt,题目难度为dt。POJ反馈状态at以0、1表示正确解答和错误解答。设交记录的独热编码长度为2N+10,若POJ反馈学生正确解答题目nt,即at=0,则提交记录中第nt个位置与2N+dt个位置值为1,其余位置为0;若POJ反馈学生错误解答题目nt,即at=1,则第N+nt个位置与2N+dt个位置值为1,其余位置为0。学生正确解答与错误解答题目的独热编码xt如图3所示。 图3 引入难度后的独热编码表示 独热编码的长度取决于数据集中题目的数量,因此在小型数据集中可以直接使用独热编码训练网络,而在大型数据集中可以通过全连接网络、自编码器与压缩感知算法进行降维处理,避免网络过拟合。 改进后模型输入为学生在POJ测试中的记录xt及对应题目的难度dt,模型输出KSt是长度为N的向量,ht为隐含层状态。ht、KSt表达式如式(3)所示 ht=tanh(Whx(xt,dt)+Whhht-1+bt)KSt=σ(Wyhht+by) (3) 式中:Whx为输入权重矩阵,Whh为循环权重矩阵,Wyh为输出权重矩阵,bt为隐藏层偏置。相较于原始模型,改进DKT模型的输入挖掘了题目的难度信息,包含更多的特征信息。 改进DKT模型的损失函数如式(4)所示 (4) 通过优化损失函数L训练网络模型,获得t时刻模型输出的KS=[ks1,ks2,ks3,…,ksN], 其中ksn是学生答对题目n的概率,代表相关知识掌握度,0≤ksn≤1。ks值越接近0,学生答对该题目的概率越小,相关知识的掌握度越低;反之学生答对该题目的概率越高,相关知识掌握度越高。因此将KS视为学生的知识状态向量,以描述学生的知识掌握度。 2.1.2 知识状态熵权计算 熵权法利用信息熵对某个指标的不确定性与离散程度客观地进行度量[23]。信息熵是事件所包含的不确定性的度量,某个指标的信息熵越小,所能提供的信息越多,表明变异程度越大,在综合评价中越重要。 熵权法是客观赋权法,精准性更强,但缺点在于仅凭数据的波动程度计算指标权重,不考虑数据的实际意义,而且不能减少评价指标的维数。DKT模型输出的知识状态向量KS中每个维度的知识掌握度实际意义相似,但在实际场景中影响学生成绩的往往是部分关键知识,直接使用知识状态向量计算学生相似关系平等对待所有知识,忽略了知识的差异性。 为了剔除知识状态向量中对学生成绩预测贡献较小的维度,本文使用熵权法处理知识状态向量,使熵权法与DKT模型发挥各自的优势。具体计算过程如下: (1)构建知识状态向量矩阵 熵权法要求对各个指标进行无量纲的标准化处理,使得数据的大小能够直观地描述评估对象的优劣情况。DKT模型输出的知识状态中知识掌握度ks值的取值范围均为[0,1],且值越大越好,属于正向指标,因此使用式(5)进行数据标准化 (5) 式中:ks′mn是学生m标准化后的ksn值,ksmn是学生m知识状态中ksn值,max(ksn) 是所有学生知识状态中最大的ksn值,min(ksn) 是最小的ksn值。 通过M个学生的N维知识状态向量构建原始知识状态向量矩阵KS′, 如式(6)所示 (6) (2)确定知识掌握度的权重 对于知识状态中每个知识掌握度的离散程度,仅考虑知识本身的重要性。依据信息熵的定义,确定各知识掌握度的熵值,如式(7)所示。其中En是第n维知识掌握度的信息熵,且0≤En≤1 (7) 在熵权法中,信息熵En被定义为潜在信息的期望值,因此定义信息效用值Dn=1-En, 则信息效用值越大,已有信息量越多,对综合评价越重要。计算第n维知识掌握度的熵权ωn*, 并构建知识掌握度熵权矩阵WE,如式(8)所示 (8) (3)计算学生的加权知识状态向量 (9) 2.1.3 相似度矩阵构建 (10) 获取所有学生的邻居学生,整体上定义学生相似度矩阵A如式(11)所示 (11) 在构建学生相似度矩阵之后,将该矩阵与POJ测试成绩输入到GCN预测网络中进行特征提取与预测,模型结构如图4所示。由于每个学生的邻居学生数量不同,难以直接使用传统卷积提取特征,因此本文使用GCN层处理不规则的邻居关系。因为单层GCN难以解决非线性问题,而层数过多会造成过平滑现象导致精度下降,并且运算量也会随之增大,不利于训练,所以设置两层GCN结构。 图4 预测网络模型 相似等级的用户在特征表现上应该相近,因此利用GCN对结点特征进行传播,特征值的信息沿着图的边之间进行传递和转换,利用邻居学生更新自身状态,本质上是聚合邻居学生信息。每一层GCN仅传播一阶邻居学生的特征信息,通过叠加多层GCN实现多阶邻居学生之间的信息传递,将未知标签学生结点的特征传播到已知标签学生的结点,因此能够利用无标签学生的邻居关系传播特征。最后使用已知标签学生的分类器计算损失函数,反向传播优化参数。 为了实现对学生的图卷积操作,本文将学生视为图中的结点,学生的POJ测试成绩视为结点特征,学生之间的相似度视为结点的连接关系,构建了学生相似度图G。通过传播式(12)融合了学生结点的POJ测试成绩与结点间的相似度关系 (12) DKT-GCN的两次图卷积操作使得结点特征可以在其二阶结邻居之间传递,使得相似的学生结点具有相似度的特征表现。学生结点的初始成绩特征H(0)在卷积操作前仅携带自身信息,在经过第一层GCN后,学生结点加权聚合一阶邻居学生的POJ测试成绩特征信息,得到特征H(1), 再经过第二层GCN加权聚合二阶邻居学生的POJ测试成绩特征,得到特征H(2)。 但在进行期末成绩预测任务时,仅使用最终层输出的特征H(2)并不能达到理想的效果。因为GCN的数学本质是拉普拉斯平滑的特殊形式,通过对结点的特征进行了低频滤波,邻居结点的特征和中心结点的特征会趋于相似,便于预测任务进行。但学生集合通常较小,随着多次使用拉普拉斯平滑之后,也就是采用了多层GCN之后,学生结点的聚合半径变大,不同学生结点的特征将趋于同质化,导致每个学生结点的局部网络结构的多样性大大降低,弱化了学生初始特征的表达,不利于结点自身特征的学习,造成过拟合。 为此本文将每层GCN的输出都与最终的聚合层相连,采用特征拼接的融合方法,将H(0)、H(1)与H(2)融合为最终成绩特征H(f)。 聚合后的结点最终成绩特征H(f)拥有混合性的聚合半径,对于任意一个学生结点而言,既不会因为聚合半径过大而出现过平滑的问题,也不会因为聚合半径过小,使得结点的结构信息不能充分学习。 最后使用式(13)计算学生的成绩组别为L的概率值TL,取其中最大概率所对应类别为预测结果。如式(14)计算所有已知标签结点的交叉熵损失函数Loss,使用Adam算法优化权重矩阵W(0)和W(1), 输出未知标签结点的预测结果 (13) Loss=-∑L∈leveltLlog(TL) (14) 为了验证模型的性能,本文某大学计算机学院2018级与2019级本科生的真实记录作为数据集,两个年级的学生整体知识状态相近。学生成绩数据集涵盖457名学生的POJ测试成绩与数据结构课程期末成绩,原始数据见表1。 表1 成绩数据集 提交数据集涵盖学生在POJ测试中的15 208条提交记录,部分原始数据见表2,其中POJstate为POJ反馈,1为错误解答,0为正确解答;proid为题目编号,具有唯一性。 表2 提交数据集 成绩数据集中期末成绩数据均为0~100的数值数据。通过对成绩数据集中期末成绩X的样本量与数值分布进行分析,在已有等级划分方法的基础上将学生m在期末考试中的成绩Xm按照式(15)分为5个等级 (15) 学生成绩数据集中存在不同场次的POJ测试满分数值不同的情况,如第一次POJ测试满分成绩为100分,而第九次POJ测试满分成绩为150分。为降低不同满分成绩对预测结果影响,提高预测模型的通用性,本文对POJ成绩进行标准化操作,标准化具体计算方法为式(16) (16) 式中:POJ′mu是学生m第u次POJ测试标准化后的成绩,POJmu学生m在第u次POJ测试中的原始成绩,max(POJu)是第u次POJ测试中所有学生的最高成绩,min(POJu)是最低成绩。 对学生成绩数据集与提交数据集进行观察分析,发现部分学生仅存在期末考试数据,其余场次的POJ成绩均为0,且提交数据集中也无对应提交记录,因此该类学生对成绩预测无意义,视为无特征结点并进行删除。同时观察到部分学生存在POJ成绩与提交记录,但期末成绩为0或者不存在数据,该部分无标签学生仅用于DKT-GCN中图卷积层。 选择了4种传统的用于学生成绩预测的机器学习模型进行了比较,以评估本文构建模型的性能。基线模型包括逻辑回归模型(logistic regression,LR)、CART决策树、支持向量机(support vector machine,SVM)、多层感知机(multilayer perceptron,MLP)。 (17) 3.2.1 参数选取 在构建学生相似度矩阵的过程中,本文通过引入阈值p定义邻居学生结点,p的取值范围为[0,1]。当p越大时,学生结点的邻居学生结点越多,通过卷积获取更多邻居学生的信息;当p越小时,学生结点的邻居学生结点越少,卷积后更多的表达自身结点信息。特别的,p=0时保留相似度最大的结点作为唯一连接,避免出现孤立结点。 图5显示了在不同p值时,RMSE值与阈值p之间的变化关系。实验结果表明p的取值对预测准确率有明显影响,并且在p=0.2时预测效果最佳,因此选择0.2作为相似度阈值。 图5 数据集RMSE变化 3.2.2 结果与分析 为比较不同时期模型预测结果的准确性,按照POJ测试时间顺序分别取前30%、前60%与所有POJ测试数据进行实验,所有实验均重复进行10次,取RMSE的平均结果作为最终预测效果。 首先仅将U次POJ测试成绩作为特征输入基线模型,而不考虑学生之间关系信息,实验结果见表3。 表3 使用POJ成绩的预测结果 将提交记录输入DKT模型获取知识状态向量,使用知识状态向量与POJ测试成绩训练模型,实验结果见表4。 表4 引入提交记录的预测结果 将题目难度输入DKT模型,将引入难度的知识状态向量与POJ测试成绩输入模型,实验结果见表5。 表5 引入难度的预测结果 利用熵权法计算知识状态向量中每个维度的权值得到加权知识状态向量,将加权知识状态向量与POJ测试成绩输入模型,实验结果见表6。 表6 引入熵权法的预测结果 实验结果显示,仅使用POJ测试成绩特征的模型预测效果较差,平均RMSE值为1.82,这是因为不同于传统的线下测试,POJ测试允许学生多次提交代码获得及时反馈,虽然最终结果相同,但是实际学生解答难度不同,仅使用POJ测试成绩特征忽略了学生提交记录,难以挖掘这些重要信息。 将学生提交记录通过DKT模型输出为知识状态向量后,传统模型综合考虑POJ测试成绩特征与知识状态特征,使得预测效果均有较大提升,平均提升13%,验证学生提交记录对使用POJ辅导教育的期末成绩预测有重要意义。 利用题目难度与熵权法对知识状态处理后预测结果更加准确,是因为通过难度特征引入了更多信息,并利用客观表现计算了不同知识掌握度的权重,使模型更关注学生区分度较大的关键知识。 GCN-DKT在所有模型中表现最为优秀,为所有预测结果中的最优值1.187,这是因为GCN能在特征传播过程中利用到无标签的学生结点,并且在模型中设置了多层特征融合,综合考虑了各个深度的特征输出,更充分地挖掘了学生做题记录中的隐藏信息。 同时发现在早期POJ测试数据的实验中DKT-GCN更具优势,这可能是因为在课程早期的POJ测试中题目往往较简单,后期表现较差的学生虽然不适应题目,但仍与表现较好的学生拥有类似的成绩特征,因此早期的测试中学生提交记录比POJ测试成绩更加重要。DKT-GCN通过对相似知识状态的邻居学生分配权重,利用图传播并约束学生特征,挖掘无标签学生的信息,降低了学生超常发挥或失误造成的POJ测试成绩波动影响,更好地预测期末成绩。 POJ的提交记录等特征难以直接量化为学生的能力水平,对于教师来说,面对不同能力水平学生的教育需要,如何进行个性化教育一直是一个难点。DKT-GCN将特征建模为加权知识状态与成绩等级,教师可以对学生进行个性化的辅导。 具体来说,成绩等级为L5与L4的学生期末不及格概率较高,教师可以在早期发现这两类高风险学生,发出风险预警并引导学生系统学习基础知识,推动其学科能力的整体提升。针对成绩等级为L3与L2的学生,教师可以分析其加权知识状态中低于平均值的部分知识,挖掘学生薄弱知识中的关键困惑因素,引导学生进行长期的与针对性的补缺学习。成绩等级为L1的学生成绩突出,远高于平均成绩,因此可以对该学生的学习需求进行升级,挖掘知识状态中较高的部分,鼓励学生围绕个人的兴趣点进行拓展学习,进一步发挥个人优势。 本文通过结合图卷积构建了一个在线编程系统学生成绩预测模型,帮助教师进行个性化教育。利用引入题目难度的深度知识追踪模型将学生的提交记录转化为知识状态特征向量,结合熵权法对题目重要性赋权。以加权知识状态计算学生相似度,将做题信息融入模型,综合考虑学生自身特征与邻居特征影响,降低了学生噪音成绩的影响。通过在真实数据集上的实验,验证了本文提出的学生成绩预测模型在POJ场景下有较好的预测效果,教师可以通过学生的知识状态与期末预测成绩,对不同成绩等级的学生进行差异辅导,提高教学质量。 后续的研究中将关注以下几点:针对不同POJ平台引入更多的个性化特征,例如通过自编码器将学生做题时间特征融入深度知识追踪模型;当前模型仅考虑知识状态的数值波动,使用更科学的度量方法可以进一步细化学生相似度结构;将结合图卷积的成绩预测模型推广到在线教育的下游任务中。
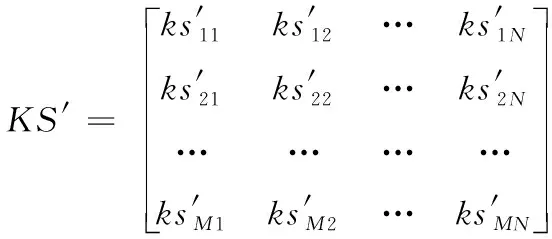
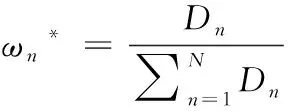
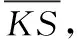
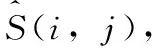
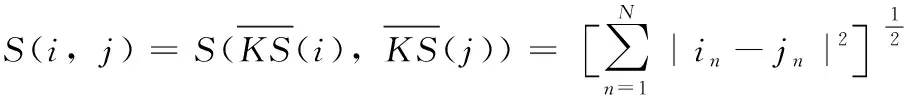
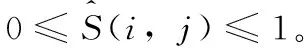
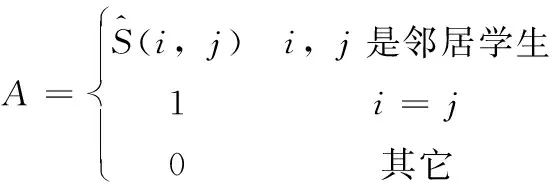
2.2 GCN预测模型的结构
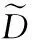
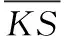
3 实验与结果
3.1 实验设置

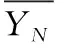
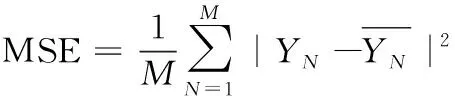
3.2 实验结果
3.3 个性化教育策略
4 结束语

