基于多重相似度和CatBoost的个性化推荐

杨怀珍，张 静，李 雷

(1.桂林电子科技大学 商学院，广西 桂林 541004；2.桂林理工大学 商学院，广西 桂林 541004)

0 引 言

推荐系统通过挖掘用户历史行为数据如购买记录、评分信息等进行个性化推荐，从而缓解“信息过载”问题[1，2]。协同过滤算法[3，4]通过分析“用户-项目”评分矩阵实现推荐。但由于历史数据存在稀疏性导致其推荐精度低[5]，针对该问题，王建芳等[6]联合用户间协同相似度、偏好相似度和具有时序的用户兴趣信息预测评分。张润莲等[7]将多种相似度加权构造混合相似度并通过K-means聚类分析来提高协同过滤推荐算法的精度。张怡文等[8]通过分析用户偏好，提出了双极协同过滤算法。任永功等[9]利用相似物品评分信息对稀疏的用户评分矩阵进行填充，然后计算近邻用户对评分矩阵进一步进行填充。Shi等[10]利用奇异值分解加加模型探讨用户可靠性和受欢迎程度等内部因素对推荐性能的影响。Nahta等[11]在协同过滤算法中嵌入元数据，Liu等[12]K-means聚类分析提取新闻内容特征并考虑新闻的受欢迎程度结合奇异值分解技术以解决协同过滤算法的数据矩阵稀疏问题。Panda等[13]提出了基于规范化的协同过滤算法。这类方法的实时性较差，主要应用在数据量相对较小的场合。

近年来，一些学者[14，15]将机器学习算法与协同过滤算法相结合，提出了基于模型的协同过滤算法。Chen等[16]利用神经网络解决了单对相互作用问题。李凌等[17]利用随机森林在不同子区域筛选特征，并由协同过滤算法进行推荐。程明月等[18]利用贝叶斯模型对协同过滤算法进行优化，提升了其预测准确性。神经网络具有良好的非线性逼近特性，王玉珍等[19]结合协同过滤算法和径向基神经网络设计推荐算法。Fu等[20]将受限玻尔兹曼机与协同过滤算法相结合用于设计推荐算法。以上算法通过挖掘历史数据的深层特征，可缓解数据稀疏性对模型的影响，然而特征提取过程耗时较多且仅采用“用户-项目”交互数据。

针对以上问题，文中在评分矩阵中融入项目元数据并由大规模信息嵌入网络(large-scale information network embedding，LINE)求解混合相似矩阵的精确近邻集，将其输入CatBoost预测项目评分并利用Top-N推荐项目。采用MovieLens数据集对评估其性能并与结合径向基神经网络的协同过滤(collaborative filtering combined with radial basis function neural network，RBF-CF)、结合XGBoost的协同过滤(collaborative filtering combined with extreme gradient boosting，XGB-CF)、基于用户的协同过滤(user-based collaborative filtering，UCF)和CatBoost进行对比。

1 推荐方法

1.1 协同过滤

协同过滤算法广泛地应用在各类推荐系统中，其依据用户或项目的历史信息实现最终的推荐。整个协同过滤推荐算法主要分为：评分矩阵构建、相似度矩阵构建和项目推荐3个阶段，相似度矩阵的构建处于核心地位，其好坏决定了推荐算法的精度。常见的相似度计量函数见表1。

1.2 结合CatBoost的协同过滤算法

CatBoost[21]是以梯度提升决策树(gradient boosted decision tree，GBDT)框架为核心的集成学习方法，具有参数量少、稳健性强等优点，常用于处理类别型变量。其通过将样本特征组合达到利用样本特征间信息的目的并采用排序提升的方法对数据进行处理降低样品数据中噪声对模型的影响。此外，该方法可解决模型过拟合的问题，提升其准确性及泛化能力。协同过滤算法能够依据用户的历史数据实现目标用户感兴趣项目的推荐。文中结合多重相似度分析和CatBoost提出了一种全新的推荐算法，其流程如图1所示。该算法具有较高的推荐精度和较强的稳定性，能够为用户准确推荐其感兴趣项目。

与传统协同过滤算法的不同之处在于，该算法首先对项目元数据和评分数据进行哈夫曼编码，将项目元数据和用户评分数据利用修正的余弦函数求出对应的相似度矩阵，并将得到的结果进行融合；然后采用LINE提取混合相似矩阵的精确近邻集并利用Skip-Gram提取其深层特征作为CatBoost的输入对项目未知评分进行预测。

阶段一：编码及相似性分析

传统的协同过滤算法直接对原始数据进行处理，会增加算法运行时间。文中采用对项目元数据和评分数据进行哈夫曼编码，以达到缩减运行时间的目的。

(1)评分数据编码及相似性分析

假设Ui为用户i，Ij为项目j，P={xi，j} 为用户i对项目j的评分，则构成的评分矩阵P见表2。

表2 用户-项目评分矩阵

(1)

(2)项目元数据编码及相似性分析

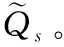
(2)

(3)混合矩阵相似性分析

大规模信息嵌入网络(large-scale information network embedding，LINE)通过求解描述一阶、二阶邻近关系目标函数的解作为节点的近邻节点，这样可以缓解稀疏数据对模型性能的影响。在LINE中相似数据结点关系如图2所示，其主要有以下两种类型：①直接相连接的结点5和结点7相似，这类结点主要位于网络顶点，采用1阶邻近关系模型进行衡量；②共享较多数量的邻近节点5和节点6相似，采用2阶邻近关系模型进行衡量。

图2 LINE网络中相似结点

一阶邻近关系模型：以混合相似矩阵Λ中项目为节点构建网络，任选网络中节点vi和vj， 则其一阶邻近关系概率为

(3)

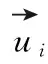
(4)

(5)

最终求解目标函数g1的最小值

(6)

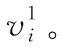
二阶邻近关系模型：二阶邻近关系模型主要用于判别共享邻近节点的相似度。通常，网络中节点还包含其它节点“上下文”，故首先采用节点vi计算节点vk生成的概率

(7)

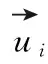
(8)

最终求解目标函数g2的最小值

(9)

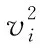
阶段二：特征向量提取

(10)

为求解其精确近邻集，对上式两边取对数，即

(11)

(12)

依据最小化式(12)对中心词向量进行优化，求解出节点vi的精确集Fvi。

阶段三：预测评分并推荐

将Skip-Gram提取的样本特征向量Fvi送入CatBoost中训练评分预测模型，其中Fvi={(X1，Y1)，(X2，Y2)…(Xn，Yn)}，n为样本个数，Xn表示第n个样本的m维特征，即Xn={x1，x2，…，xm}；Yn为第n个样本的属性。在建立预测模型时首先利用数值s替换类别型变量，其中s为

(13)

然后对其弱学习器进行训练，最终使损失函数的值趋于0。也就是说CatBoost最终是使ht最小，即

(14)

式中：ht为CatBoost中的弱学习器，Ft-1(x) 为上一轮训练得到的强学习器。经过多次循环迭代最终得到的CatBoost模型为

Ft(x)=Ft-1(x)+ht

(15)

2 模型评价

MovieLens数据集中包含有1682部电影且943个用户对电影的评分，评分值为0～5之间，此外统计了电影的标题、类型和主演等信息。文中以MovieLens数据集为实例，随机选取MovieLens数据集中20%的数据作为测试集、80%的数据作为训练集进行评估实验，并与RBF-CF、XGB-CF、UCF和CatBoost对比来进一步验证文中方法的有效性。

2.1 评价指标

文中采用预测精度、平均绝对偏差和运行时间作为评价指标，对各模型的性能进行评估。其中，预测精度用于评估用户喜欢的项目在推荐项目总数中的占比，其值越大说明模型性能越优，反之模型性能越差；平均绝对偏差用于衡量项目预测评分和项目实际评分的差值，其值越小说明项目预测评分越接近项目真实评分，反之项目预测评分与项目实际评分差距越大。预测精度(Precision)和平均绝对偏差(mean absolute error，MAE)计算公式可表述为

(16)

(17)

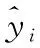
2.2 模型参数确定

(1)相似度函数确定

选择合理的相似度函数可准确求解出评分相似矩阵和项目元数据的相似矩阵，从而提高推荐模型的预测精度、降低平均绝对偏差。利用欧几里得函数、余弦相似度函数、修正的余弦函数和皮尔逊函数求解的评分相似矩阵和项目元数据相似矩阵的预测精度如图3所示。从图中可看出，与欧几里得函数、余弦函数和皮尔逊函数相比，修正的余弦函数求解的相似矩阵用于模型预测评分具有更高的精度，因此文中采用修正的余弦函数作为求解相似矩阵的衡量标准。

(2)CatBoost中决策树个数确定

CatBoost选用决策树作为其弱学习器对项目的评分进行预测，最终利用投票决策的方式求解出项目的预测评分。较少的决策树数目会降低CatBoost对项目的预测精度，然而较多的决策树数目则会增加CatBoost的运行时间。表3给出了决策树数目为50～450时CatBoost的预测精度及运行时间。从表中可看出，当CatBoost中决策树数目小于300时，随着决策树数目的增加CatBoost的预测精度和运行时间均增加且决策树数目为300时CatBoost的预测精度最高；当CatBoost中决策树数目超过300后，CatBoost的预测精度并未明显增加但运行时间却大幅增加，故而文中将CatBoost中决策树数目设定为300。

表3 不同决策树数目下模型的预测精度和运行时间

2.3 实验结果分析

通过与RBF-CF、XGB-CF、UCF和CatBoost对比，从预测精度、运行时间和平均绝对偏差3个方面对各模型的有效性进行评估。RBF-CF、XGB-CF、UCF、CatBoost和CatBoost-CF(文中所提算法)在不同近邻集数目下的预测精度见表4。从表中可看出，随着近邻集数目的增加，各模型的预测精度均逐渐增加。此外，在不同近邻集数目中，CatBoost-CF的预测精度均最高、XGB-CF和RBF-CF的预测精度次之，UCF的预测精度最差。这主要是由于CatBoost-CF模型在评分数据中融入了项目元数据，并且采用修正的余弦相似度函数和LINE求解的项目近邻集更准确，从而提高了模型的预测性能；XGB-CF中采用集成学习的策略，能够提升模型的非线性建模能力；RBF-CF中采用神经网络抽取用户评分历史数据的深层特征，可缓解评分数据稀疏性导致的模型预测精度低的问题。

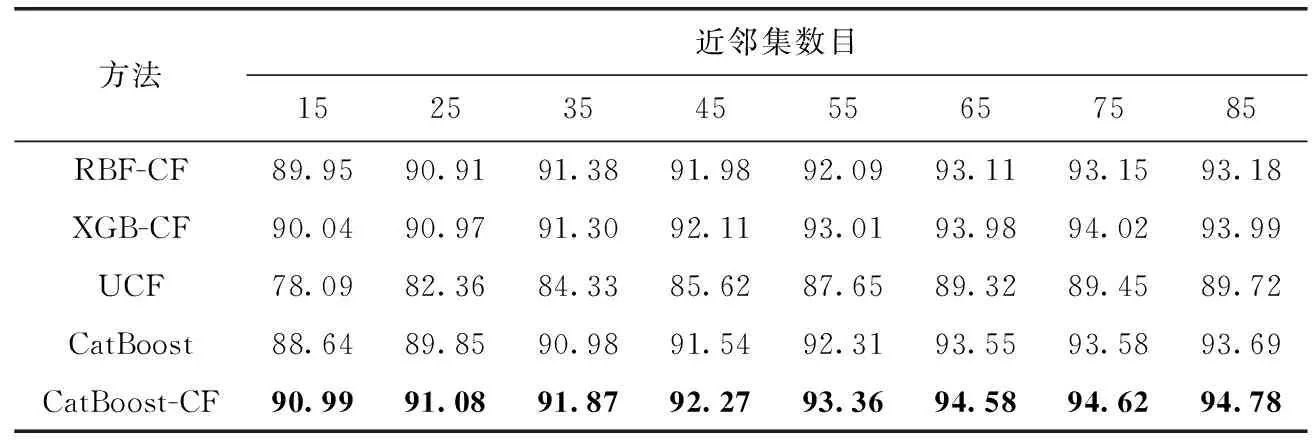
表4 不同近邻集数目下各算法的预测精度

RBF-CF、XGB-CF、UCF、CatBoost和CatBoost-CF在不同近邻集数目下的运行时间见表5。从表中可容易的看出，UCF的运行时间最短，这主要是由于UCF直接采用相似矩阵进行预测评分无需其它操作；CatBoost-CF的运行时间较UCF和CatBoost的运行时间长，这主要是由于CatBoost-CF需要经过LINE网络求解多阶相邻节点。RBF-CF和XGB-CF的运行时间相当且前者运行时间更长，这主要是由于RBF神经网络需要多次迭代寻优而XGB中包含多棵决策树需要多次运算出最优结果。

表5 不同近邻集数目下各算法的运行时间

为进一步说明CatBoost-CF在各阶段的耗时，文中以近邻集数目为85时进行实验，其各阶段及总运行时间见表6。从表中可看出，CatBoost-CF中阶段三耗时最多、阶段一耗时次之、阶段二耗时最少。这主要是由于CatBoost需要经过多个弱学习器进行项目评分的预测最后再投票决策，而阶段一耗时则主要是由于LINE网络迭代求解多阶近邻节点。

表6 CatBoost-CF在近邻集为85时各阶段的运行时间及总运行时间

模型的稳定性决定了模型预测结果的可靠性，文中以MAE作为RBF-CF、XGB-CF、UCF、CatBoost和CatBoost-CF算法稳定性的衡量标准，各算法在不同近邻集下的MAE值如图4所示。从图中可看出，随着近邻数集个数增加各推荐算法的MAE均逐渐降低，这说明随着训练集样本增加，各模型的稳定性也逐渐增强。此外，在不同近邻集数目下CatBoost-CF的MAE均低于对比方法，XGB-CF次之，UCF的MAE值最高。这主要是评分数据中融入了项目元数据并由修正的余弦相似度函数和LINE精确求解项目的近邻集，从而增强了CatBoost-CF的稳定性。然而传统的UCF直接采用评分数据进行预测评分而近邻集数目越大其越不精确故而稳定性最差。RBF-CF和XGB-CF的MAE值相当且优于UCF，说明集成学习和神经网络均可以改善模型的稳定性。

图4 各算法在不同近邻集下的MAE

3 结束语

文中结合多重相似度分析和CatBoost提出了一种推荐算法，该算法具有较高的推荐精度、较强的稳定性。与传统推荐算法不同的是，其采用修正的余弦相似度函数和LINE求解项目元数据和评分数据的精确近邻集并由Skip-Gram挖掘其深层特征输入CatBoost中预测项目评分最终由Top-N算法推荐项目。最后，采用MovieLens数据集对该算法性能进行评估，结果表明，该算法推荐精度更高、稳定性更强，可缓解数据稀疏性带来的推荐质量低的问题。但是该算法较对比方法运行时间较长，在后续工作中尝试将该算法并行化处理以缩短其运行时间。