基于样本分布的类别均衡化方法
李国和,陈桂婷,郑艺峰,洪云峰,周晓明,潘雪玲
(1.中国石油大学(北京)石油数据挖掘北京市重点实验室,北京 102249;2.中国石油大学(北京)克拉玛依 信息科学与工程学院,新疆 克拉玛依 834000;3.闽南师范大学 计算机学院,福建 漳州 363000;4.杭州拾贝知识产权服务有限公司 应用研究院,浙江 杭州 310010;5.厦门瀚影物联网 应用研究院,福建 厦门 361021)
0 引 言
获取知识精度不仅与机器学习算法有关,还深受数据质量的影响,如样本类别的不均衡性,导致机器学习获取的分类模型把少数类样本误判为多数类,从而影响了分类模型有效性[1-3]。样本均衡化方法分为算法层面[4]和数据层面[5]。前者改进学习算法,样本不发生变化;后者对样本本身增加或减少。欠采样容易丢失多数类样本的分类信息,因此过采样是主流的均衡化方法,得到广泛研究和应用。
启发式的SMOTE[6]算法随机选择少数类样本的近邻样本,通过线性插值生成新样本,但未考虑近邻样本的空间分布。G-SMOTE[7]算法先对少数类样本聚类,为每个类簇分配合成样本数量,在少数类样本的超球体区间合成新样本,重构了样本空间。GJ-RSMOTE[8]算法采用高斯混合模型和JS散度共同控制合成样本的数量和分布,但凹分布考虑不足。SMOTE-LOF[9]算法通过添加局部异常因子LOF对SMOTE算法进行改进,避免噪声样本的生成。基于最优路径森林的无监督过采样算法[10]先通过聚类获取少数类样本的内部分布,然后使用均值和协方差矩阵合成新样本,保证了样本的多样性。K-means SMOTE[11]通过K-means聚类,根据给定阈值删除少数类与多数类样本数占比低的少数类样本簇,有效抑制新少数类样本落入多数类区域,但没考虑少数类内部的分布。
针对过采样算法存在的问题,提出类别均衡化方法(label-balancing method based on sample distribution,LBMSD),主要包括净化少数类分布边界;确定少数类合成样本数和平衡少数类类簇间的样本数量;分配少数类簇样本权重,决定类簇内生成少数类样本及其合理分布。
1 相关概念
1.1 信息系统与信息决策系统

如果集合div(X)满足X=∪∀xi∈div(X)Xi且Xi≠Xj,Xi∩Xj=∅,称div(X) 为X的划分。对于IS,属性集A⊆S, 存在划分div(X) 满足∀a∈A,∀Xi∈div(X),∀u,v∈Xi,a(u)=a(v), 称div(X) 为基于属性集A的等价划分,记为X/A。 如果∀a∈A为连续或数值型,样本相似度simA(u,v)≤δ, 称div(X) 为基于属性集A的聚类划分,记为cluA(X)。 对于DT,决策属性∀d∈D为离散型,存在基于D′⊆D的等价划分,记为X/D′。 |X/D′| 为决策类别数(|.|为集合元素个数)。条件属性∀c∈C为连续或数值型,存在基于C′⊆C的聚类划分,记为cluC′(X)。
对于DT,∃Xi,Xj∈X/D,|Xi| 与 |Xj| 差异较大,称DT为类别不均衡决策信息系统。当 |X/D|=2时,如果 |X1|>|X2|, 则X1为多数类样本集,记为N(负例样本集);X2为少数类样本集,记为P(正例样本集)。DT可分解为Kp=
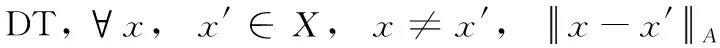
1.2 单类支持向量机
单类支持向量机One-class SVM[12]采用核函数把样本映射到高维特征空间,将零点作为负样本点,其它样本作为正样本点,最大化零点和其它样本点之间的距离并构建最优超平面。对于N={x1,x2,…,xn} 负例样本集,One-class SVM优化目标如式(1)所示
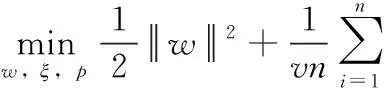
(1)
式中:v∈(0,1) 为调节松弛程度,控制异常样本比例的上界,w是超平面法向量,ρ是超平面截距,φ() 为原始空间到特征空间的映射。ξ是松弛变量,允许一定误差的存在。
1.3 DBSCAN算法
对于Kp=
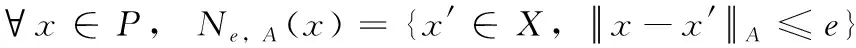
定义2 核心点:∀x∈P,Ne,A(x)≥φ时,其中φ为e邻域中样本数阈值,x为基于属性集A、φ的核心点,记为CNe,A,φ(x)。
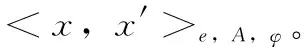

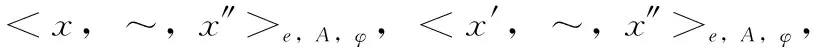
由上述概念构成密度聚类DBSCAN算法核心,可实现Kp的聚类划分cluA(P)。
2 类别均衡化过采样方法LBMSD
类别均衡化过采样方法过程:①判断信息决策系统DT的不平衡度,根据不平衡度的大小选择不同的方法清洗数据;②利用DBSCAN对P得到聚类划分cluA(P), 计算类簇密度和边界样本数确定类簇生成样本数;③区分类簇的边界和非边界样本集,并分别确定样本分布概率;④根据分布概率选取种子样本,使用SMOTE算法生成新样本。
2.1 数据清洗
为了防止过拟合和类别重叠问题出现的概率,应要过滤异常样本进行数据清洗。本算法首先判断信息决策系统DT的不平衡度,当不均衡度大于特定阈值t时在DT中使用近邻法识别异常样本;小于t时利用训练One-class SVM模型来识别Kp, 并删除Kp中KN识别为正常数据的样本得到Kp=
近邻法是通过统计样本的k个最近样本的类别个数n,如果k等于n,就判定样本为异常样本。
2.2 类簇过采样数量
由于在样本空间中每个类簇中的样本分布各不相同,会造成类别内部分布不均衡,因此使用DBSCAN密度聚簇算法对正例样本进行划分,针对不同类簇的密度和边界样本的数量,自适应为其分配一定的权重。对于密度稀疏的类簇采样较多的样本以提高识别率,对边界样本数量多的类簇采样较多的样本以扩充样本的空间分布。
定义6 类簇密度和采样倍率:Kp=
(2)
过采样倍率为归一化类簇密度倒数,如式(3)所示
(3)
WD表明类簇的采样数与类簇密度成负相关。
定义7 边界样本占比:类簇Xi⊆cluA(P) 的边界样本集borderk(Xi)={x|∀x∈Xi,|KNNA,k(x)∩N|>k/2}。 边界样本占比表明正例类簇归一化的边界样本比例,如式(4)所示
(4)
WB表明正例类簇归一化的边界样本比例。
定义8 类簇权重:类簇Xi⊆cluA(P) 的权重为过采样倍率和边界样本占比的加权和,如式(5)所示
Authorityk,λ(Xi)=λ×WBk(Xi)+(1-λ)×WDk(Xi)
(5)
式中:λ为调节因子。类簇权重Authorityk,λ(Xi) 综合考虑类簇密度和边界分布。当λ>0.5时,更关注边界分布;当λ=0.5时,边界样本占比和密度分布的重要性相同。类簇权重函数综合考虑了类簇密度和边界分布情况,合理控制新样本的分布,为新样本选取安全区域。
合成正例样本数量numsum,δ=(|N|-|P|)×δ。 其中δ∈[0,1] 为均衡化程度,控制合成正例样本的数量。当δ值为1时,正例样本数量与负例样本数量相同。
每个类簇的过采样数量计算如式(6)所示
numk,δ,λ(Xi)=Authorityk,λ(Xi)×numsum,δ
(6)
式中:Authorityk,λ(Xi) 控制不同类簇生成不同数量的样本,不同的类簇根据上述公式合成不同数量的样本。
2.3 分布概率生成与种子样本选取
采用样本的k个近邻情况可将每个类簇分为边界样本集和非边界样本集,并分别计算集合中合成正例样本的数量;然后根据样本的相对密度自适应生成分布概率,并通过样本的分布概率选取种子样本;最后采用SMOTE算法进行样本合成,以提高识别精度。分布概率大被选为种子样本的几率就大,保证了样本分布的多样性,重构了样本的总体分布。
对于∀Xi⊆cluA(P) 中borderk(Xi) 边界种子数量计算如式(7)所示
(7)
Xi-borderk(Xi) 非边界种子数量计算如式(8)所示
num_nobork,δ,λ(Xi)=numk,δ,λ(Xi)-num_bork,δ,λ(Xi)
(8)
∀x∈P, 对于Kp和KN, 相对密度为类簇中正例样本数与负例样本数之比。相对密度表示了样本的近邻情况,当样本的近邻样本中正例样本数小于负例样本数时,则样本的相对密度小,反之相对密度大。计算如式(9)所示
(9)
其中为了避免样本的k近邻样本中没有负例样本的情况,上述公式使正例样本数与负例样本数分别加1。
边界样本x∈borderk(Xi) 分布概率如式(10)所示
(10)
非边界样本x∈Xi-borderk(Xi) 分布概率如式(11)所示
(11)
样本的分布概率决定了样本被选为种子样本的可能性。若一个样本的分布概率越大,此样本被选为种子样本的几率越大;反之,此样本被选为种子样本的几率越小。具体过程如算法1所示。
算法1:P_SMOTE
输入:正例集P,样本集X,样本个数M,分布概率pC,k, 近邻数k
输出:生成正例样本集P′
(1)P′=∅ //生成样本集
(2) fori=1 toMdo: //生成样本个数
(3)xl=random.choice(X,pC,k) //根据分布概率选取样本种子
(4)P′=P′∪SMOTE(P,xl,k) //生成样本
(5) end for
(6) returnP′
2.4 LBMSD算法流程
LBMSD主要流程包括以下3个部分:①使用近邻法和单类支持向量机进行数据清洗;②使用DBSCAN聚簇并计算每个类簇的密度和边界样本数量,自适应地生成样本数量;③根据计算分布概率选取种子样本并使用SMOTE算法生成新样本。完整流程如算法2所示。
算法2:LBMSD
输入:决策信息系统DT,近邻个数k,样本e邻域中样本数阈值φ,均衡化程度δ,类簇权重调节因子λ,均衡度阈值t
输出:均衡化后样本集
(1)Ptemp=∅ //新增正例集
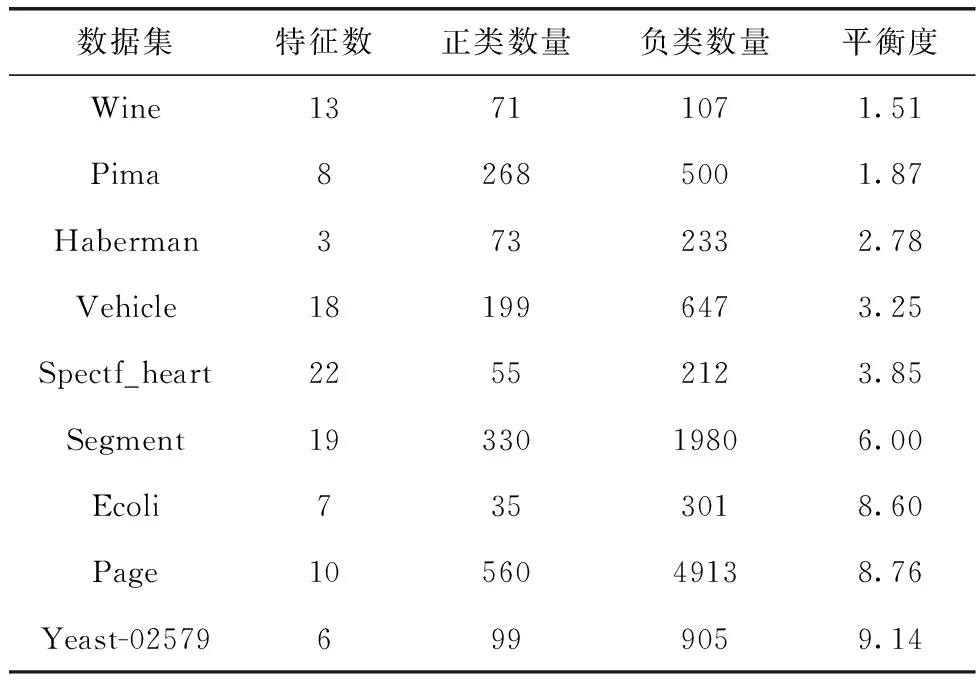
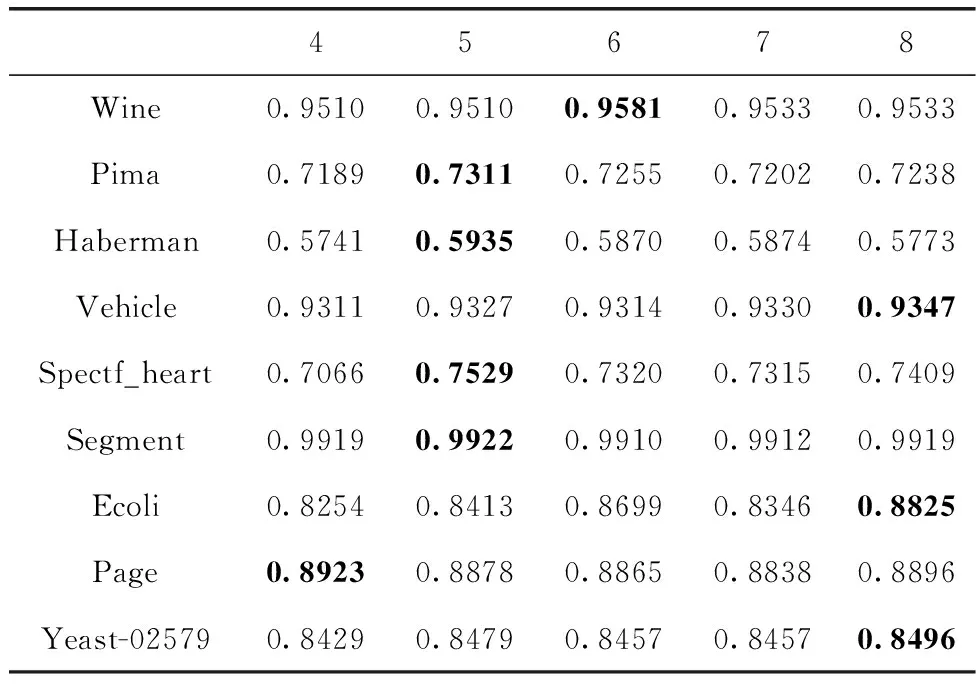
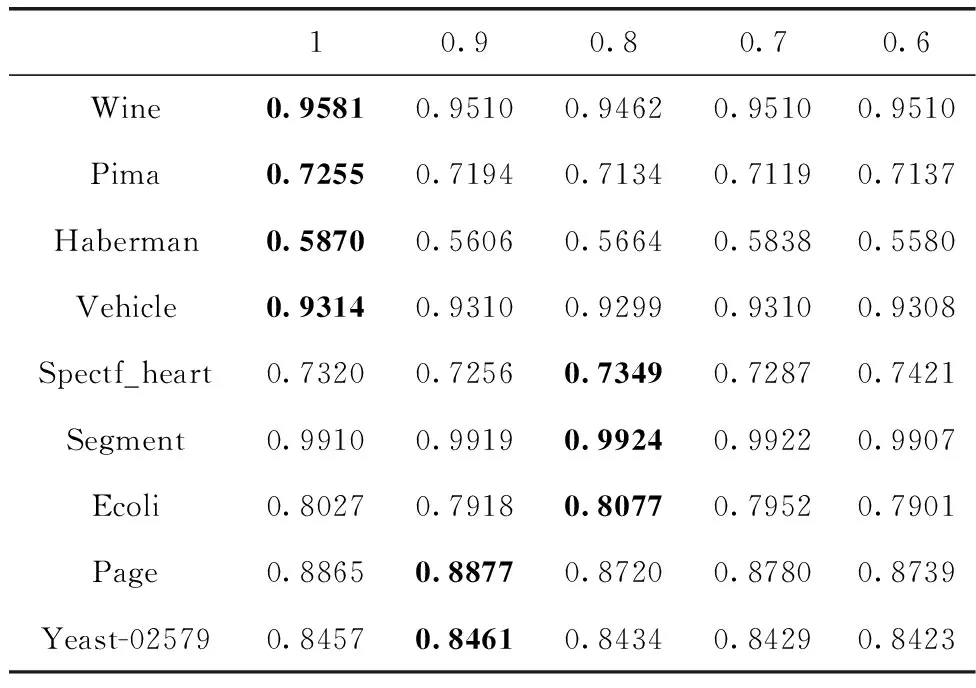
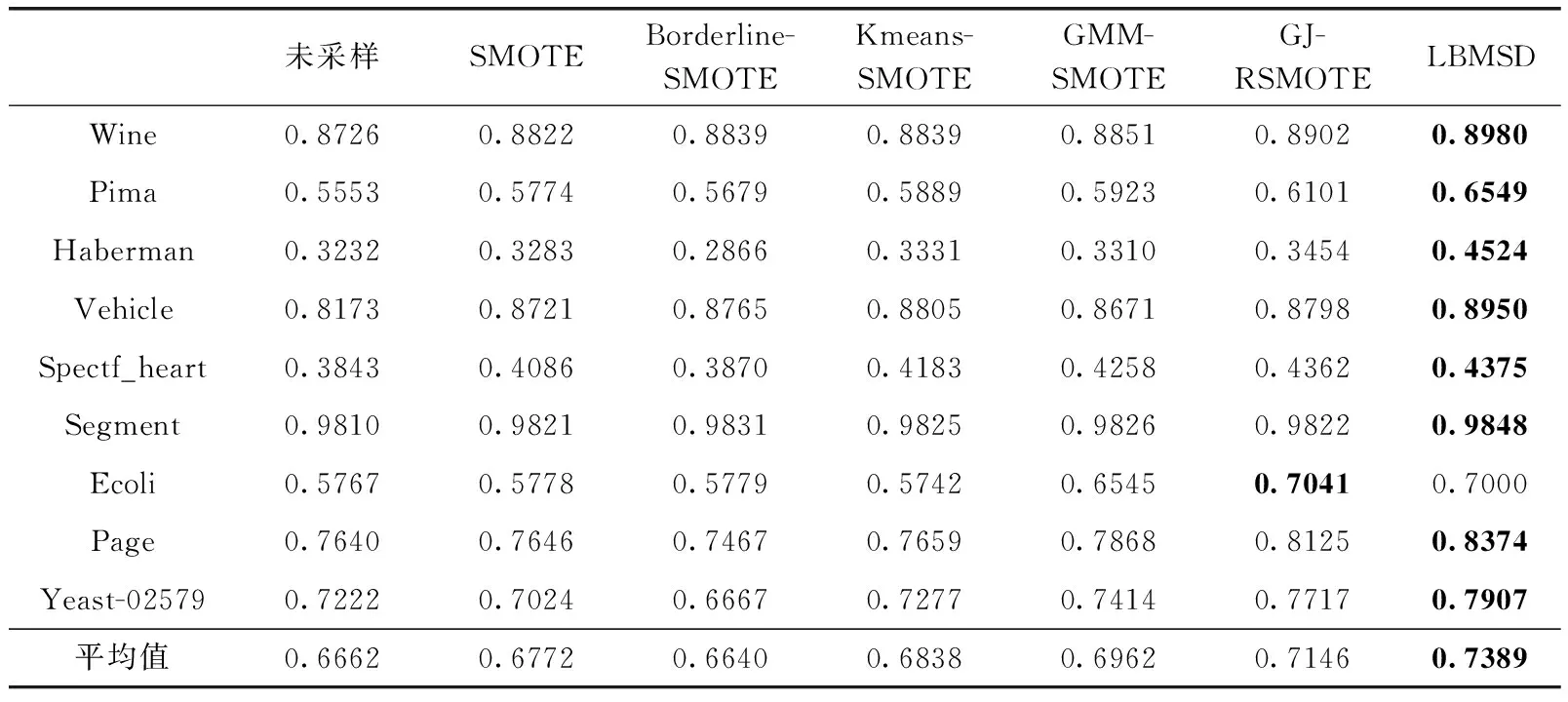
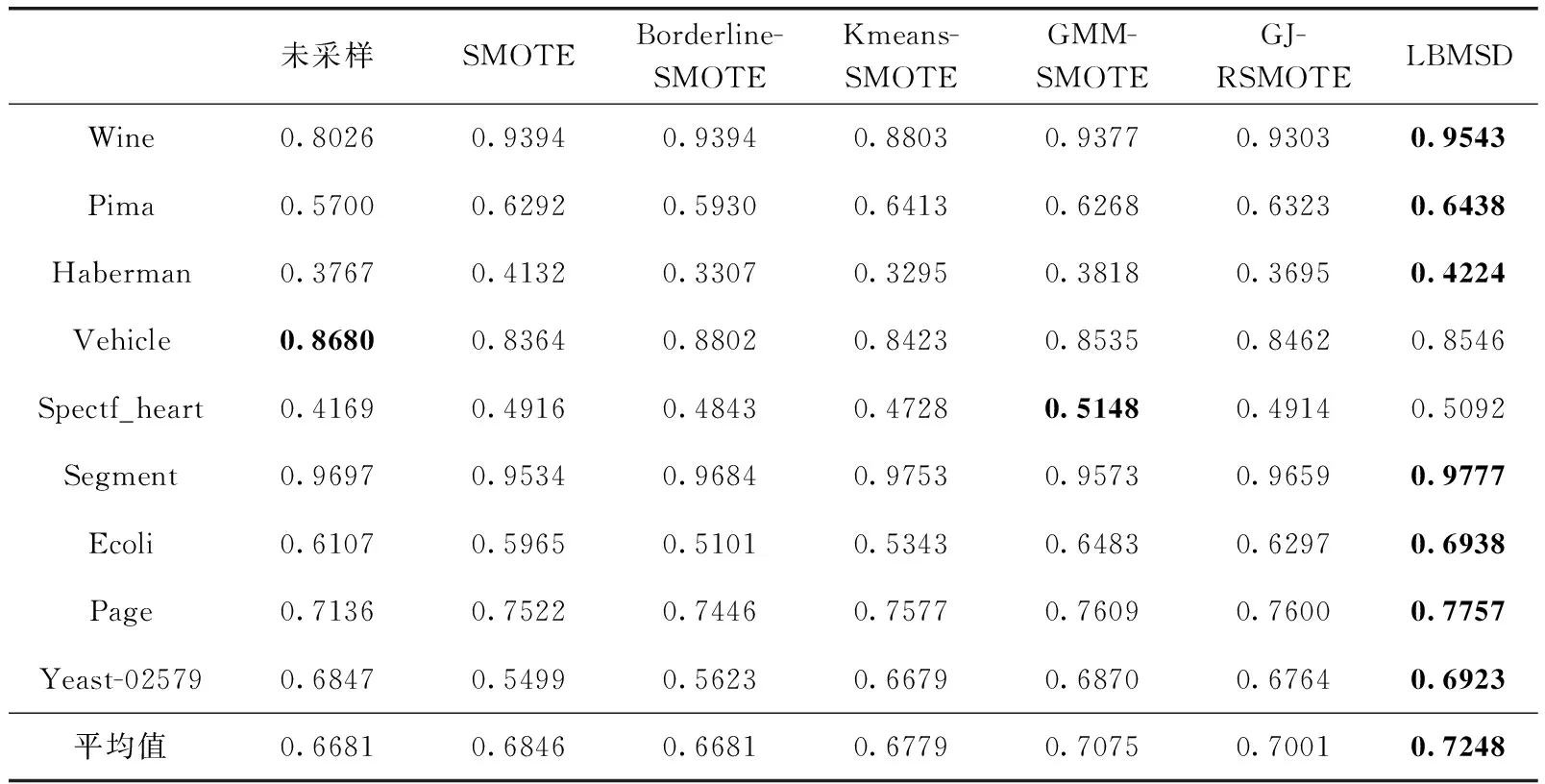
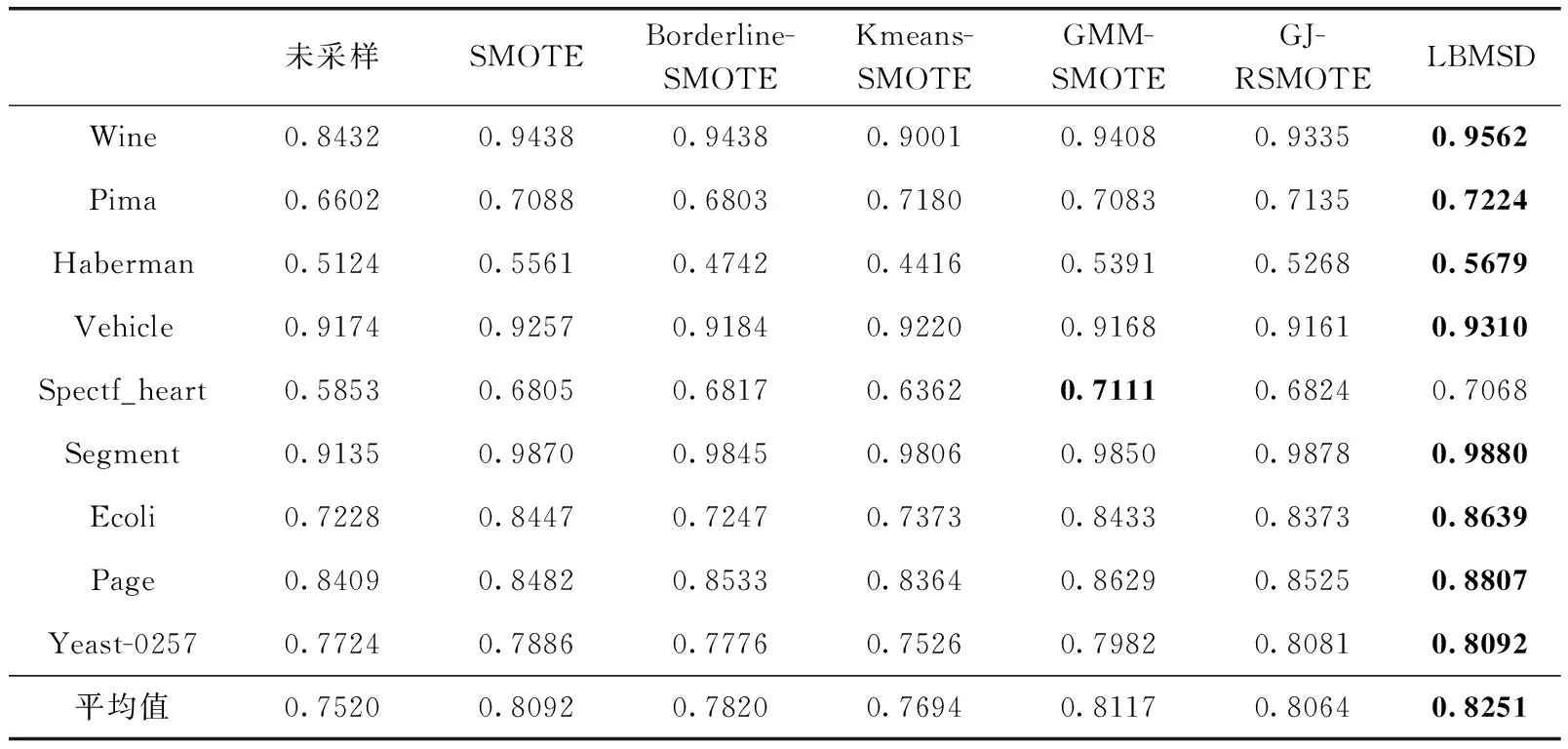
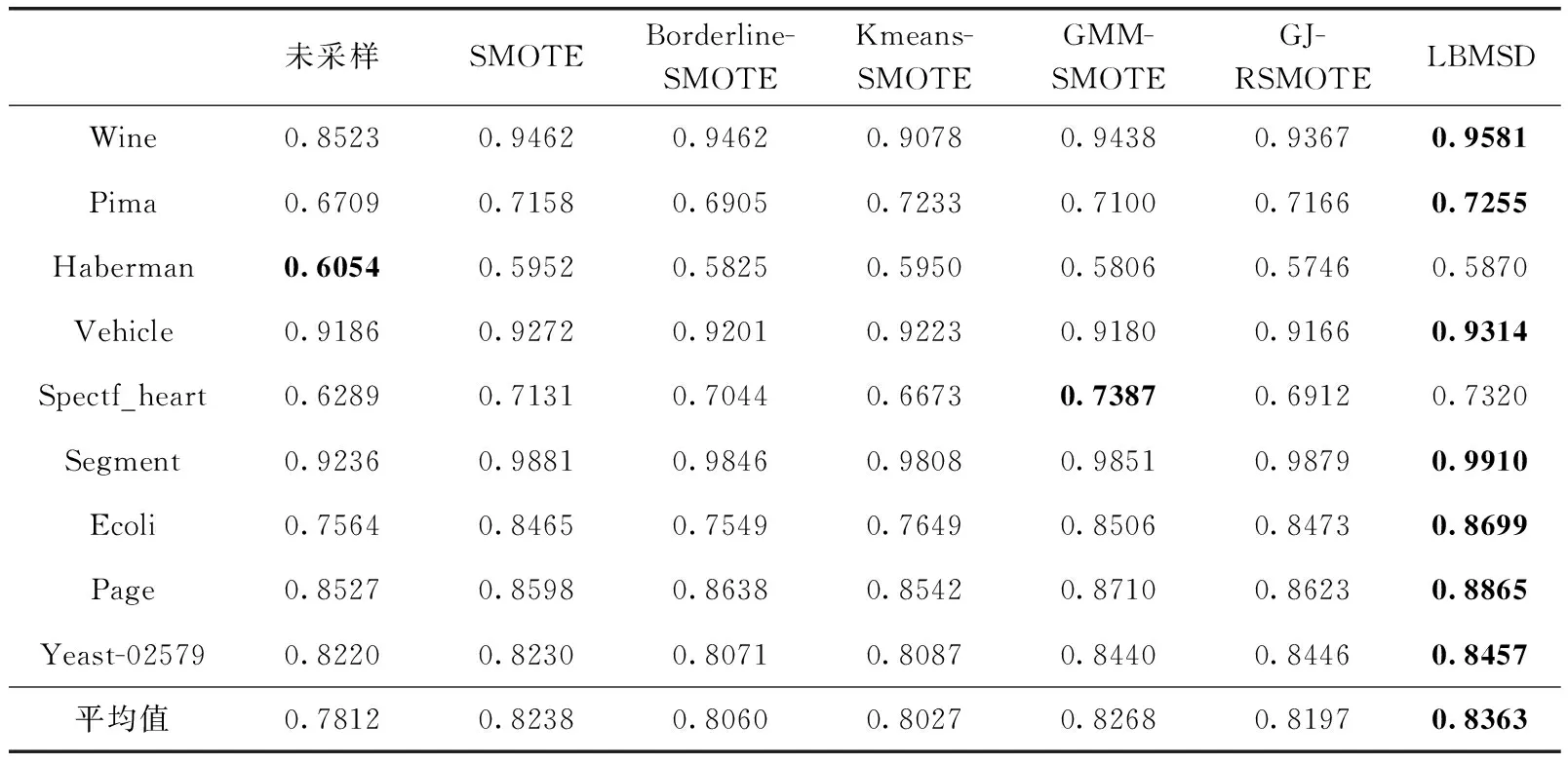
(2) if |N|/|P| (3) model=One-class SVM.fit(N) //训练负例样本 (4)P=P-model.predict(P) //删除异常样本 (5) end if (6) else then //不均衡度高于t (7) for ∀x∈Nthen (8) ifKNNA,k(x)∩P==k//k近邻法判定异常样本 (9) deletex (10) end for (11)cluC(P)=DBSCAN.fit(P,φ) //正例样本聚类 (12)numsum,δ=(|N|-|P|)×δ//总过采样数 (13) for ∀Xi⊆cluC(P) then //遍历正例类簇 (14)X′=borderk(Xi) //边界样本集 (15)M′=num_bork,δ,λ(Xi) //边界样本集生成样本数 (16)P′=P_SOMTE(P,X′,M′,bor_pA,k,k) //边界新样本集 (17)X″=Xi-borderk(Xi) //非边界样本集 (18)M″=num_nobork,δ,λ(Xi) //非边界样本集生成样本数 (19)P″=P_SOMTE(P,X″,M″,nobor_pA,k,k) //非边界新样本集 (20)Ptemp=Ptemp∪P′∪P″ //新增正例样本集 (21) end for (22) returnP∪N∪Ptemp//均衡化样本集 对9组UCI数据集进行实验(如表1所示),其中不平衡度为负例样本与正例样本的数量比值。 表1 数据集信息 本文分类器性能评价参数是基于表2所示的混淆矩阵定义所得到。 表2 混淆矩阵 分类模型评价的精确度(precision)、召回率(recall)计算如式(12)、式(13)所示 (12) (13) 精确度高表示负类判断为正例的比例低,召回率高表示正例判断为负例的比例低。 F-measure为召回率和精确率的调和均值,计算如式(14)所示 (14) G-mean为召回率和真负率TNR的几何平均值,综合了两个类别的准确率,计算如式(15)所示 (15) ROC曲线分别以TPR、TNR为纵轴和横轴,AUC是ROC曲线下的面积,评估分类模型性能。AUC的取值范围为[0.5,1],AUC越接近1说明算法的真实性越高。本文采用F-measure、G-mean、AUC为分类模型的评价标准。 LBMSD参数包括近邻k值和均衡化程度δ值。 (1)近邻k值 实验参数的设定在一定程度上影响算法的性能,k值的大小决定了类簇边界样本集的划分,从而影响到均衡化效果。针对不同k值,采用KNN(k=5)分类器以及AUC评价指标进行实验,结果见表3。实验结果表明,对于不平衡度低的数据集,k为5时均衡化效果最优;对于不平衡度高的数据集,k为8时均衡化效果最优。由此可知,k的取值对不同数据集的分类性能的影响程度不同。 表3 不同k值使用KNN分类器的AUC值对比 (2)均衡化程度δ值 针对不同均衡化程度,设置均衡化程度值的大小从0.6到1,采用KNN分类模型及其AUC评价进行实验(如表4所示)。实验结果表明,对于数据集不平衡度较低时,δ值为1时分类器的性能表现较好;对于数据集不平衡度较高时,δ小于1时分类器的性能表现较好。实质上,样本类别均衡化是重构正例样本的合理分布,使本该不同类别有些差异的样本均等化后,反而不符合原有分布规律。样本类别不均衡也是客观事实,均衡化也不可“矫枉过正”,导致原有类别分布仍然不合理,所以在均衡化过程中要分析数据中正例样本与负例样本的分布,根据样本的特性合理地选择均衡度。 表4 不同均衡化程度使用KNN分类器的AUC值对比 采用SMOTE、Borderline-SMOTE、Kmeans-SMOTE、GMM-SMOTE、GJ-RSMOTE和LBMSD进行对比实验。设置样本邻域k为6,均衡度为1,DBSCAN半径e为1,最小包含点数φ为5,不平衡度阈值t为6。采用C4.5,KNN(k=5)分类模型进行五折交叉验证,使用F-mea-sure、G-mean、AUC评价指标。实验结果如表5至表10所示。从实验结果分析,达到均衡度为1时,LBMSD都可以取得较好效果,尤其原始数据集均衡度很差时,如Page、Yeast-02579,LBMSD均衡化效果更加明显。LBMSD综合考虑了分布边界清晰化、不同类簇的分布,有效提高了识别精度。 表5 不同算法使用C4.5分类器的Kmeans-SMOTE、F-measure值对比 表6 不同算法使用C4.5分类器的G-mean值对比 表8 不同算法使用KNN分类器的F-measure值对比 表9 不同算法使用KNN分类器的G-mean值对比 表10 不同算法使用KNN分类器的AUC值对比 随着计算机技术的快速发展,在人们生产生活中能源变成一种必不可少的物质。虽然太阳能、风能等新能源技术越来越成熟,但是像石油、天然气等传统能源的储备也是不可或缺的。对地震相分析并进行岩性识别是油气勘探认识地层构造、储层性质的重要内容[14]。岩性信息能够反映出油气储存位置以及流体特征,在地层储层预测和油气勘探中具有重要作用。由于在同一区域的地层数据反映了同一个岩性信息,所以可以根据同一区域的岩性信息来预测这一地区的储油情况,极大地减少了人力物力资源。 根据地层中岩石的成分、颗粒大小、结构、孔隙度等参数表征可以把地层分为不同的岩性[15]。岩性作为地层岩石的主要特征,可将岩石划分为砂岩、泥岩和其它岩性。岩性不同,构成颗粒大小不同,孔隙度也不同,因此储存油气的能力也不同。砂岩的特点是强度低,颗粒粗,吸水率高,所以油气等资源易存储于孔隙度相对大的砂岩地层中[16]。在对地震相岩性识别研究时,主要关注点是可以储存油气的砂岩地层,然而砂岩在地层中所占比例很少,造成数据的类别不均衡问题。当机器学习算法预测岩性时可能会导致识别精度不理想,所以在地震相岩性识别之前对数据进行均衡化处理尤为重要。 地震数据来自华北油田某地区,共1956道,501个采样点,采样率为2 ms,构成数据集(如表11所示)。对于地震数据,当均衡度设置为1时,识别精度最高(如表12所示)。采用C4.5和KNN分类模型分别进行十折交叉验证,使用F-measure、G-mean、AUC作为算法评价指标,实验结果见表13。从实验结果分析可知,与其它过采样算法相比,LBMSD过采样算法在多个评价指标中表现优异,有效提升了分类模型的性能。 表11 地震相数据集 表12 不同均衡度对应的KNN识别效果 表13 地震相岩性识别效果 样本类别均衡化核心是合理控制新生成样本合理的数量及分布,并真实反映了样本的分布。LBMSD均衡化主要包含4个过程:通过单分类支持向量机和近邻法删除噪声样本,优化正例样本分布边界;密度聚类正例样本,通过每个类簇的密度和边界样本数量,确定每个类簇需要生成的样本数;通过每个类簇边界和非边界分割,并确定各自分布的生成样本数;根据样本分布概率确定生成的样本数并选取种子样本进行样本合成。样本类别均衡化不同于样本类别均等化,下一步工作是研究自动确定均衡度,获得最佳均衡化效果。3 实验结果与分析
3.1 数据集与评价指标

3.2 实验参数设定
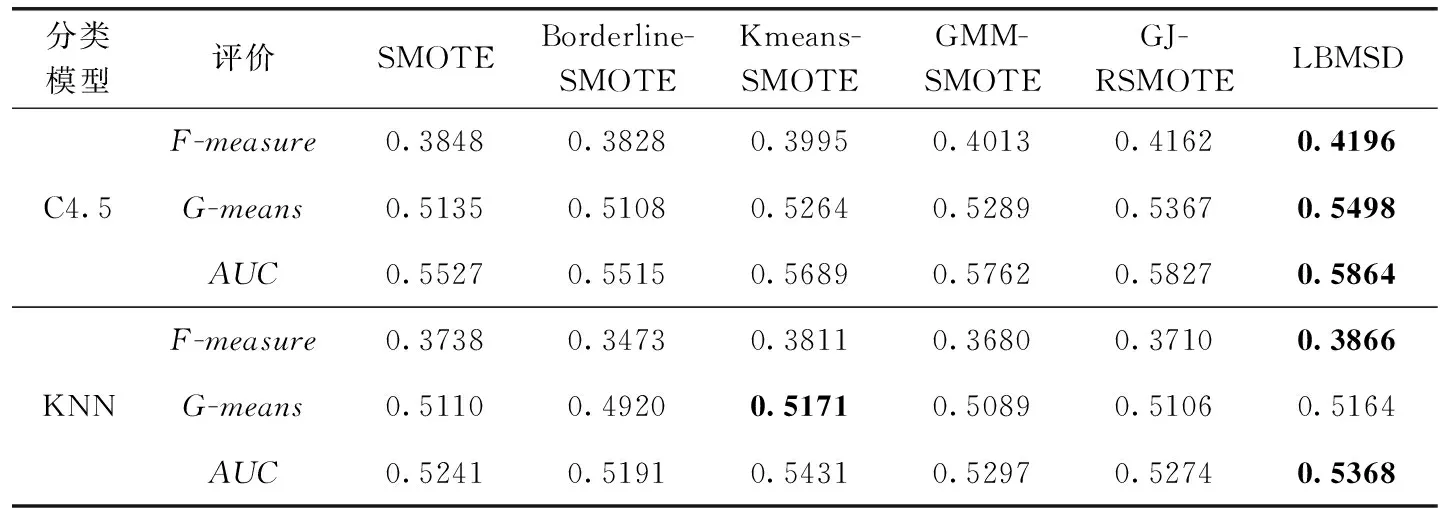
3.3 不同均衡化方法实验对比

3.4 地震相岩性识别应用


4 结束语

