Lump solution and interaction solutions to the fourth-order extended(2+1)-dimensional Boiti-Leon-Manna-Pempinelli equation

Wenxia Chen,Yi Wang and Lixin Tian

Nonlinear Scientific Research Center,Faculty of Science,Jiangsu University,Zhenjiang,Jiangsu 212013,China

Abstract In this paper,we explore the exact solutions to the fourth-order extended (2+1)-dimensional Boiti–Leon–Manna–Pempinelli equation.Based on Hirota bilinear method,lump solution,periodic cross-kink solutions and bright-dark soliton solutions were investigated.By calculating and solving,the peak and trough of lump solution are obtained,and the maximum and minimum points of each are solved.The three-dimensional plots and density plots of periodic cross-kink solution and bright-dark soliton solution are drawn and the dynamics of solutions under different parameters are observed.

Keywords: Hirota bilinear method,eBLMP equation,lump solution,interation solution

1.Introduction

Nonlinear science is an interdisciplinary subject which researches the commonness of nonlinear phenomena.Its rapid development promotes the development of related fields of mathematical physics.With the development of soliton theory,solitons have become an important branch of nonlinear science.Soliton equations can describe many nonlinear phenomena,for example,they play an important role in nonlinear mechanics,fluid optics,Marine science and other fields.So it is an important subject to study the nonlinear waves and exact solutions of soliton equations,such as Schödinger equation[1,2],Korteweg–de Vries equation [3,4],Boussinesq equation [5] and so on.With the deepening of the research,the development of nonlinear wave theory is promoted,especially in the Chen–Lee–Liu equation [6] and Manakov system [7–10],which show a lot of the latest progress of nonlinear wave theory.Many exact solutions have also been proposed,such as soliton solution,lump solution,rogue wave solution,periodic wave solution,breather solution,bright and dark soliton solution and so on.Lump wave [11–13] and rough wave[9,14,15]are both local waves.Rough waves are localized in space and time,while lump waves are only rational function waves localized in space.The interaction between lump waves and some solitary waves will lead to many new interaction solutions.They collide after interaction,and we can observe many interesting physical phenomena by drawing them.

In recent years,many methods have been found to solve the exact solutions of soliton equations.For example,Hirota bilinear method [16–18],Generalized bilinear method[19,20],homogeneous balance method [21,22],Riemann–Hilbert method [23–25],Darboux transformation [26–28],Riccati expansion method [29,30] and so on.Hirota bilinear method is a common method to solve soliton equations,and Ma has solved many soliton equations with lump solutions and exact solutions by Hirota bilinear method [31].Generalized bilinear method was proposed by Ma in 2015.Batwa and Ma used this method to solve the lump-type and interaction solutions of the (3+1)-dimensional Jimbo–Miwa-like equation [20].Recently,Riemann–Hilbert method has been widely used to solve soliton solutions of equations.Explicit soliton solutions of a higher-order Chen–Lee–Liu equation[25],N-soliton solutions for the Maxwell–Bloch equations[32] are obtained by this method.

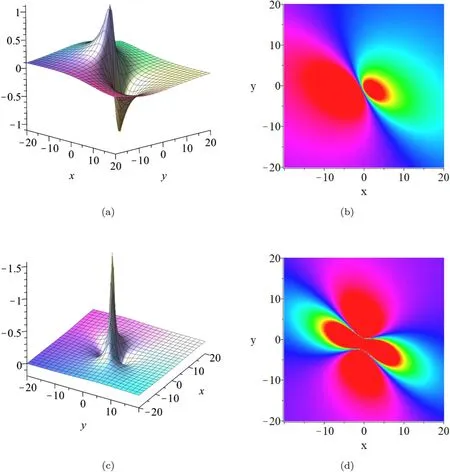
Fig. 1.Plots of lump solution u (a) three-dimensional plot;(b) contour plot.Plots of lump solution v (c) three-dimensional plot;(d)contour plot.

In this research,we focus on the fourth-order extended(2+1)-dimensional Boiti–Leon–Manna–Pempinelli (eBLMP)equation [33],given as

whereci(i=1,2,3,4) are arbitrary constants.The fourthorder eBLMP equation describes a physical phenomenon in nature,namely the evolution of nonlinear shallow-water wave propagation.It is widely used in optical fiber,traffic flow and other physical phenomena.Ren [33] has given the Hirota bilinear method of eBLMP equation,solved the eBLMP equation with WTO method,and obtained the D’Alemberttype wave and solitary wave.Through the following transformation

the bilinear form of equation (1) gives

It is not difficult to rewrite equation (3) into the following equivalent form

Select c1=1,c2=c3=c4=0,and from equation (1),we obtain the (2+1)-dimensional BLMP equation [34].This equation is closely related to the KdV equation.Select c3=0,and from equation (1),we obtain the (2+1)-dimensional ePBLMP equation [35].BLMP equation is an important integrable model,which is widely used in physics and engineering phenomena such as fluid,traffic flow and plasma.Recently,some new interaction solutions to(2+1)-dimensional BLMP have been obtained by using the Hirota bilinear method [36].The (3+1)-dimensional BLMP equation[37]describes the formation of liquid and its exact solutions are obtained by bilinear method.There are many ways to solve the BLMP equation such as discovering the exact solutions to (2+1),(3+1) and (4+1) dimensional time-fractional BLMP equations through the extended tanh method [38].The exact multiwave solutions to BLMP equation are constructed by multiple exp-function method[39].The mixed lump-soliton solutions to BLMP equation are obtained by the Generalized bilinear method[40].Some interation solutions to eBLMP equation are obtained by the Hirota bilinear method [41].

The outline of our article is organized as follows.In section 2,solve the lump solution to the (2+1)-dimensional eBLMP equation,provide appropriate parameters,draw threedimensional and density plots of the solutions u and v,and calculate their extreme points.At the same time,we also analyze the motion paths of the lump wave at different time t.In section 3,two groups of periodic cross-kink solutions are calculated,and the dynamic paths of the solution at different times are analyzed,and the influence of different parameters on the periodic cross-kink solution is discussed.In section 4,two groups of bright-dark soliton solutions are calculated,and the appropriate parameters are selected to draw the threedimensional plots and density plots of the bright-dark soliton solutions u and v,and analyze the trajectory of the solution u at different times.In section 5,we summarize the whole article.

2.Lump solution to the eBLMP equation

In order to get the lump solution to equation(1),the following quadratic function can be assumed

where ai(i=1,2,3,4,5,6,7,8,9) are constants to be determined.

Substituting expression (5) into (4),then equating all coefficients of x,y,t.Letting x,y,t have coefficients of different powers of zero,then we can get a set of nonlinear algebraic equations about ai(i=1,2,3,4,5,6,7,8,9).After solving the system of equations,we obtain some values of the parameters as:

where ai(i=1,2,4,6,7,8),c1,c2,c3are real number that satisfy a1≠0,a6≠0 and a7≠0.By means of transformation (2),the lump solution to equation (1) can be obtained

The parameters are selected as

The solutions of u and v are shown in figure 1.We can observe the local characteristics of the lump solution at t=0.From figure 1,it can be seen that the lump wave of u has one peak and one trough,and is highly symmetrical,while the lump wave of v has one trough and two peaks.

The critical points of the lump wave are solved

By solving the above condition (9),we find two extremum points of u as

Explicitly,the above two critical points are symmetrical at the point

Similarly,we can find three extreme points of v as

Then,we figure out the Hessian matrix and vyyat point(x1,y1) as

and the Hessian matrix and vyyat point(x2,y2)and(x3,y3)as

Therefore,the v at the extreme point(x1,y1) is the minimum value of lump solution,that is,the trough depth is

and the v at the extreme points(x2,y2) and(x3,y3) are the maximum value of lump solution,that is,the peak height is

The moving path of the lump wave can intuitively describe the moving of the lump solution.By solving fx=fy=0,we can obtain the moving path of the lump wave in (7).The exact moving path of the lump wave is written as

Fig. 2.The moving path of the lump wave u is at(a)c2=1,(c)c2=-3.The moving path of the lump wave v is at(b)c2=1,(d)c2=-3.

3.Periodic cross-kink solutions to the eBLMP equation

In order to find periodic cross-kink solutions to equation (1),we assume that

where k1,k2,k3,k4are arbitary constants,and g,h and n are defined as follows

where ai(i=1,2,3,4,5,6,7,8,9,10,11,12) are arbitary constants to be determined.Substituting expression(17)into(4),then equating all coeffciients of e-g,eg,sin (h),cos (h),sinh (n),cosh (n).Letting e-g,eg,sin (h),cos (h),sinh (n),cosh(n) have coefficients of different powers of zero,then we can get a set of nonlinear algebraic equations about ai(i=1,2,3,4,5,6,7,8,9,10,11,12).The symbolic computing software Maple is used to solve the above algebraic equations,and the following two groups of solutions were obtained.

Case 1:

wherek i(i=2,3,4),a j(j=1,3,4,6,8,9,10,12) and c1,c2are arbitary constants and a10≠0.By means of transformation(2),the periodic cross-kink solution to equation(1)can be obtained

wherek i(i=1,2,3,4),a j(j=1,2,4,6,8,9,12) and c1,c2,c4are arbitary constants and a2≠0.By means of transformation(2),the periodic cross-kink solution to equation(1)can be obtained

The characteristics of the periodic cross-kink solution with time t=-4,0,2 are shown in figure 3.It can be seen from figure 3 that with the increase of time t,the periodic cross-kink wave propagates in a certain direction.In figure 4,we change the values of parameters k1,k2,k3and k4,and it is observed that the change of parameters has certain influence on the periodic cross-kink solution (21).Compared with figure 3(b): in figure 4(a) k1is turned negative,the periodic cross-kink waves move down,the peaks get shorter and the amplitudes decrease.In figure 4(b) k2is turned positive,and the periodic cross-kink waves move upward and the amplitude increases.As k3in figure 4(c)increases to 2,the periodic cross-kink waves move upward and the amplitude increases markedly.When k4in figure 4(g) changes to -20,the amplitude of the periodic cross-kink waves increases and the periodic cross-kink waves spread out.

4.Bright-dark soliton solutions to the eBLMP equation

In order to find bright-dark soliton solutions to equation (1),we assume that

where k1,k2,k3are nonzero real numbers,and g,h and n are defined as follows

where ai(i=1,2,3,4,5,6,7,8,9,10,11,12,13)are arbitary constants to be determined.

Substituting expression (23) into (4),then equating all coefficients of sinh (g),cosh (g),sin (h),cos (h),sinh (n),cosh(n).Letting sinh (g),cosh (g),sin (h),cos (h),sinh (n),cosh(n)have coefficients of different powers of zero,then we can get a set of nonlinear algebraic equations about ai(i=1,2,3,4,5,6,7,8,9,10,11,12,13).After calculation,we get the following two sets of solutions.

wherea i(i=1,4,6,8,10,12),k2,k3and c1,c2,c3are real number that satisfy a1≠0,a6a10≠0.By means of transformation(2),the bright-dark soliton solution to equation(1)can

be obtainedwhere

wherea i(i=4,5,6,8,10,12),k1,k2,k3and c2,c3are real number that satisfy a5a6≠0.By means of transformation(2),the bright-dark soliton solution to equation (1) can be obtained

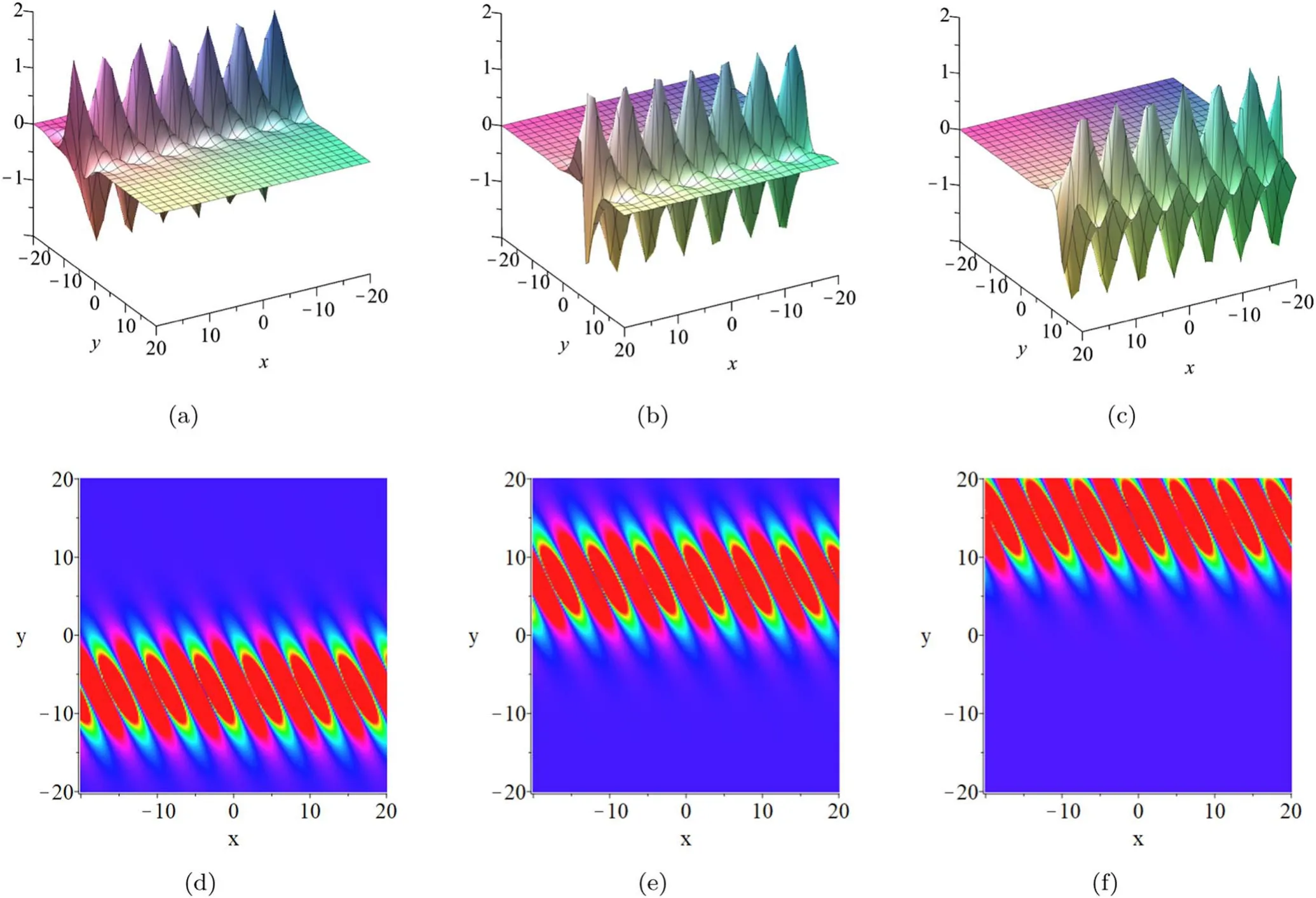
Fig. 6.The bright-dark soliton solution (28) takesk1 =,k2 =- 5,k3=3at t=-3,4,8.

The characteristics of the bright-dark soliton solutions with t=0 are shown in figure 5.In addition,the motion trajectories of bright-dark soliton solution u at different time can be observed through figure 6.We can find that the bright-dark soliton solution u maintains its shape and amplitude unchanged during the propagation process.

5.Conclusion

In this paper,we explore the exact solutions to the fourthorder extended (2+1)-dimensional eBLMP equation.First of all,the bilinear form of the eBLMP equation was obtained by Hirota bilinear method,and the lump solution to the equation was calculated,two symmetric extreme points of u and three extreme points of v were obtained.At the same time,the moving path of the lump waves were plotted and analyzed.Secondly,two sets of periodic cross-kink solutions were obtained,and the motion states of the solution at different times were analyzed.Different parameters were selected to compare the three-dimensional and density plots of the solution,and the effect of the parameters on the solution was observed.Finally,two groups of bright-dark soliton solutions were obtained by calculation,and the motion states of the solution at different times were analyzed.Other knowledge of eBLMP equation will be studied and explored carefully in the future.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No.11731014).

Declaration of interests

The authors have no conflicts of interest to declare that are relevant to the content of this article.