Comprehensive analysis of relativistic embedded class-I exponential compact spheres in f(R,φ) gravity via Karmarkar condition

Zoya Asghar,Adnan Malik,M Farasat Shamir and Fatemah Mofarreh

1 National University of Computer and Emerging Sciences,Lahore Campus,Pakistan

2 School of Mathematical Sciences,Zhejiang Normal University,Jinhua,Zhejiang,China

3 Department of Mathematics,University of Management and Technology,Sialkot Campus,Pakistan

4 Mathematical Science Department Faculty of Science Princess Nourah bint Abdulrahman University,Riyadh 11546,Saudi Arabia

Abstract In this article,we use the prominent Karmarkar condition to investigate some novel features of astronomical objects in the f(R,φ)gravity;R and φ represent the Ricci curvature and the scalar field,respectively.It is worth noting that we classify the exclusive set of modified field equations using the exponential type model of the f(R,φ) theory of gravity f(R,φ)=φ(R+α(eβR-1)).We show the embedded class-I approach via a static,spherically symmetric spacetime with an anisotropic distribution.To accomplish our objective,we use a particular interpretation of metric potential (grr) that has already been given in the literature and then presume the Karmarkar condition to derive the second metric potential.We employ distinct compact stars to determine the values of unknown parameters emerging in metric potentials.To ensure the viability and consistency of our exponential model,we execute distinct physical evolutions,i.e.the graphical structure of energy density and pressure evolution,mass function,adiabatic index,stability,equilibrium,and energy conditions.Our investigation reveals that the observed anisotropic findings are physically appropriate and have the highest level of precision.

Keywords: stellar structures,metric potentials,f(R,φ) theory of gravity,Karmarkar condition

1.Introduction

The rapid evolution of the cosmos is one of the most intriguing dimensions of study in astrophysics in recent years.According to astrophysicists,the Universeʼs energy structure is 20% dark matter (DM),76% dark energy (DE),and 4% ordinary matter(OM) [1–4].Whereas DM pressure is nearly nonexistent compared to the DEʼs strong negative pressure.Cosmologists believe that dark energy is the primary factor causing the Universeʼs enigmatic evolution.Although general relativity(GR) offers a basic concept of gravitational notions and produces excellent results in a relativistic theory,it is not sufficient when dealing with difficulties like the unknown DEʼs exotic nature.These gravitational theories are acknowledged as the modified theories of gravity and the most suitable replacement for GR.Various modified theories available in the literature include f(R),f(R,T),f(R,φ),f(R,G),f(R,φ,X) and f(R,RαβRαβ,φ)gravitational theories[5–31].It is interesting to note that astronomers plan to study the collapsing attributes of celestial configurations with the asset of modified gravitational theories.Buchdahl [13] introduced the f(R) gravity,which modifies the Einstein action by utilizing any arbitrary Ricci scalar function.The exponential-type gravity models were introduced by Cognola et al [32] to investigate the physical attributes of astronomical formations.Harko [7] introduced the f(R,T) gravity theory,which is an amalgamation of the curvature or matter.Sharif and Ikram [33] presented f(G,T) gravity and probed the stability attributes.Capozziello and Laurentis[34],who also talked about f(R,φ) gravity,first proposed the scalar field in action.They argued about a unique method for resolving and addressing GRʼs flaws.The nature of relativistic compact structures in the f(R,φ)gravity was studied by Shamir,and Malik [35].Various literature has been available related to scalar-tensor theories [36–41].The modified f(R,φ) gravity,which specifies the structure of the inner space,was studied by Malik [42] to determine how charged compact stars behave.

Cosmologists illustrated various theories about the formation of stellar objects.Gravitational forces occurring at the core of compact stars are intensely exothermic.This reaction occurs when the interior pressure of the realistic structure falls to preserve the pressure against the exterior gravitational implosion.Distinct types of intense stars,including white dwarfs,gravastars,neutron stars,black holes,or quark stars,appeared due to the imploding stars.These stars are categorized according to their masses and are an intriguing issue within the background of modified theories.Although the precise nature of these things is yet unclear,one might surmise that they are massive objects with small radii.To explore the exotic nature of such stellar configuration models,we require an accurate outcome to Einstein field equations(EFE),which was first computed by Schwarzschild [43] in 1916.Afterward,Tolman [44] and Oppenheimer [45] provided a detailed review of celestial structures.They claimed that the physical properties of astrophysical configurations demonstrated the interaction between inner pressure and gravitational force,which preserves an equilibrium condition.Baade and Zwicky [46] were among the first researchers to discuss the idea of cosmic star structure.Later,Ruderman [47]investigated the celestial sphere in the source of anisotropic fluid and declared that the density of nuclear elements shows anisotropic behavior at the center.A perfect isotropic fluid was believed to be the basis of stellar systems in the formation of astrophysical structures.These stars are classified as stellar,isotropic,spherically symmetric,and highly heavy objects.But still,some physical elements of compact stars may not be expressed by this isotropic feature.In astronomy,the anisotropic fluid is gaining much attention as a worthy substitute for isotropic matter distribution.Anisotropy is assumed as the fluid due to the combination of distinct types of fluids,magnetic field,viscosity,rotation,etc.Bowers and Liang[48]discussed the notion of non-zero anisotropy in the creation of stars.Furthermore,Ruderman [47] was the first to propose that the celestial structureʼs high density illustrates the anisotropy at the stellar objectʼs core.Various literature has been presented in the context of anisotropic distribution[49–53].Also,the anisotropic pressures are categorized into radial and transverse distributions.

Astrophysicists used the EFE explanatory method to investigate a four-dimensional manifold family that transforms into Euclidean space for a well-behaved astronomical structure. Nash [54] discovered the first isometric embedding theorem.Later,Gunther [55] provided a modified version of this theorem.Gupta and Sharma [56] utilized the plane metric to obtain the embedded class method.The Karmarkar condition is a differential equation that the embedded classes develop in spherically symmetric spacetime that comprises both the potential components,i.e.grrand gtt.The mentioned condition was introduced by Karmarkar [57] and is defined as R1414R2323=R1212R3434+R1224R1334.There is a vast amount of literature on the Karmarkar condition.Maurya et al [58] and Bhar et al [59]examined the response of astrophysical objects in the analysis of GR by using Karmarkar and embedded class-I conditions.Sharif and Saba [60] explored the Karmarkar condition in f(G)gravity along with the anisotropic charged solution,and their results are symmetric and consistent.Naz et al [61] studied the possibility of a unique variety of embedding class-I results of astrophysical objects by utilizing the Karmarkar constraints in the f(R) gravity.Asghar et al [62] probed the different stellar structures in f(R,T)gravity with the help of the Karmarkar condition.Rahaman et al [63] examined the embedding class-I solution for studying the anisotropic structures by implementing the Karmarkar requirement in the f(R,T) gravity.Singh et al[64] apply an embedding approach to explore the graphical features of sphere configurations in f(R,T) gravity.After getting motivated by the prior literature,we further extend the Asghar et al [62] notion in modified f(R,φ) gravity by implementing the Karmarkar condition to examine the physical attributes of various stellar stars.For the present analysis,we consider the exponential f(R,φ)gravity model,i.e.f(R,φ)=φ(R+α(e-βR-1))[32].Also,using a precise solution for the metric potential grr[65] that has already been published in the literature,we employ the well-known Karmarkar condition to calculate the second metric potential.

The format of our profile is as follows: in the next part,the modified EFEʼs,as well as a realistic model of f(R,φ)theory,are explored in the light of the Karmarkar condition.Section 3 is concerned with junction conditions for obtaining constants by contrasting the internal geometry to Schwarzschildʼs external spacetime.The graphical study is described in section 4,which includes the anisotropic component,stability analysis,Tolman–Oppenheimer–Volkoff equation (TOV),equation of state parameters,mass–radius connection,and surface redshift analysis.We finalized the key findings in the concluding portion.

2.Modified f(R,φ) field equations via Karmarkar condition

The scalar-tensor theories [66] are a fascinating group of extended theories of gravity.This subsection provides an overview of the f(R,φ)theory of gravity and discusses how it applies to static spherically symmetric stellar structures.The following effective action results in a wide range of higherorder scalar-tensor theories [67] as

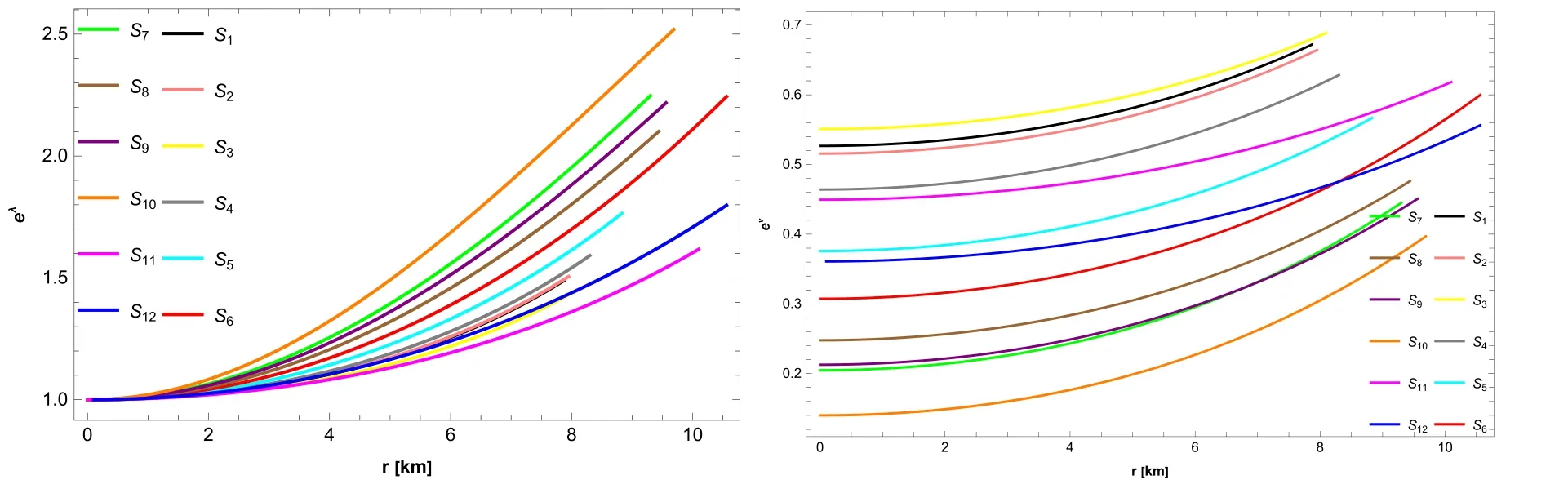
Fig. 1.Behavior of metric potential grr and gtt.

Here,f(R,φ) is a function that depends on curvature R and scalar field φ.Also,-g illustrates the determinant of gηζ.The EFEʼs of f(R,φ) are derived by varying the action in equation (1) concerning the metric tensor.

Here,ν and λ are only the functions of r.Moreover,to investigate the consistency and equilibrium of the compact system,we examine an exponential model of the f(R,φ)gravity,which assists us in getting a comprehensive performance of the formation of realistic structures.The exponential f(R,φ) gravity model [32] is depicted as

Here,α and β are unknown parameters and φ ≡rχ.We assume w(φ)=w0φm,where m can be any non-zero value.It is worth noting that the consideration of the Klein–Gordon equation (3) is required for the relevant outcomes.Also,the spacetime metric reveals the class of an embedded class-I and whether it fulfilled the prominent Karmarkar condition [57],which is stated as

with R2323≠0.By substituting the Riemann tensor components into equation (7),we get the succeeding differential form

The integration of the above gives the following form of equation

where,A and B are integrating constants.We presume a specific value of the metric potential grr=eλ(r)[65] to calculate the results of embedded class-I

where,a and b can be any non-zero constant parameters.When equation(10)is substituted for equation(9),the metric potential eνhas the value

Furthermore,to investigate the implications of our chosen f(R,φ)model,we examined the essential requirements for the metric tensors of static spherically symmetric spacetime,namely eλ(0)=1 and((eλ(r)) ′)r=0=0.The physical structure of grrought to be free of singularities,uniform,and monotonically increasing for a realistic f(R,φ) gravity model.Figure 1 shows the physical nature of eλ(r),which increases monotonically and attains its highest value towards the boundary.Hence,using equations (6),(10),and (11),themodified f(R,φ) field equations stated in equation (2) yields

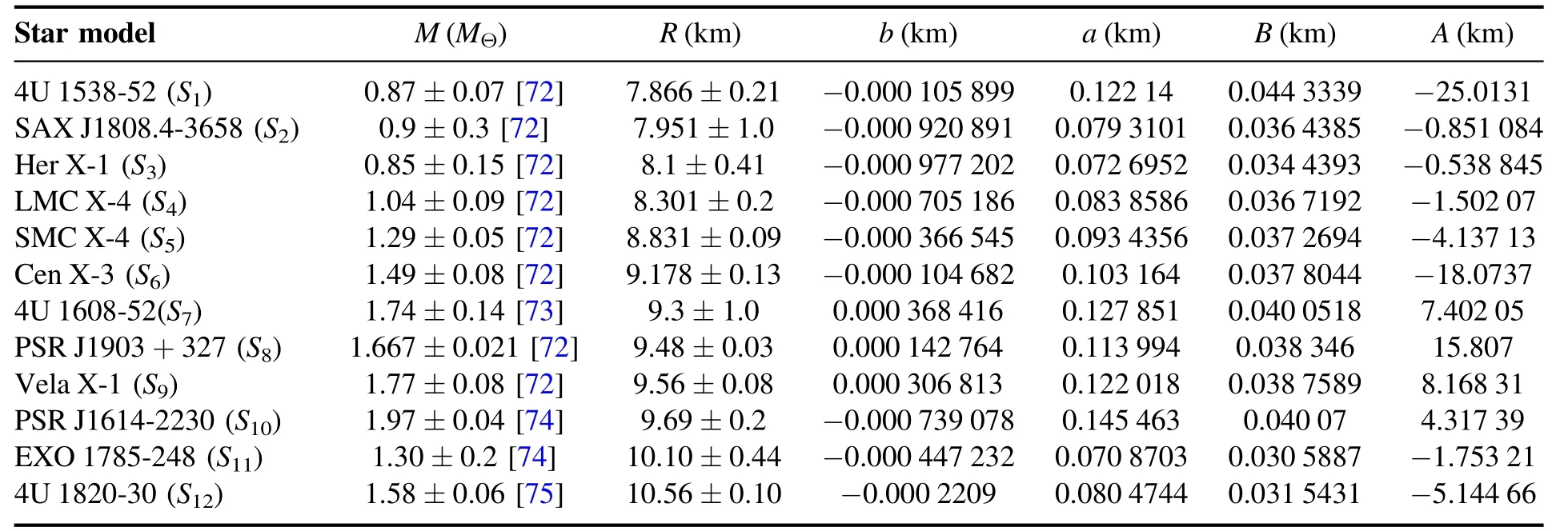
Table 1.Unknown parameters of the compact structures.

Here,

3.Junction conditions

Whatever the geometry of the star is,either derived internally or externally,the intrinsic boundary metric remains the same.Thus,ensuring that the elements of the metric tensor irrespective of the coordinate system across the surface of the boundary will remain continuous.No doubt,in GR,the Schwarzschild solutions have been pioneers in guiding us to choose from the various possibilities of the junction conditions while exploring the celestial stars.Now when we come to the case of modified theories of gravity,modified TOV equations with zero pressure and energy density,the solution outside the star can vary from Schwarzschildʼs solution.However,it is expected that the solutions of the modified TOV equations [44,45] with energy density and pressure(maybe non-zero)may adjust Schwarzschildʼs solution with some distinct preference of f(R,φ)gravity model.Perhaps this is the reason that Birkhoffʼs theorem may not hold in modified gravity [68].The detailed examination of the issue in f(R,φ) gravity can be an interesting task.Many authors have assumed the Schwarzschild solution for this purpose giving some impressive outcomes [1–71].Now to solve the field equations under the restricted boundary essentials at r=R,the pressure pr=0,the internal metric (5) needs these matching conditions.To resolve the EFE with the limited restriction at r=R,we contrast our inner geometry to the exterior Schwarzschild solution,which is described by

where,M is the mass of compact sphere.The continuity of metric parameters of equation (5) at r=R emerges in the governing equations:

In this case,(+) and (-) represent the external and internal structures.We use equations (5),(12),and (13) to calculate the values of the parameters as

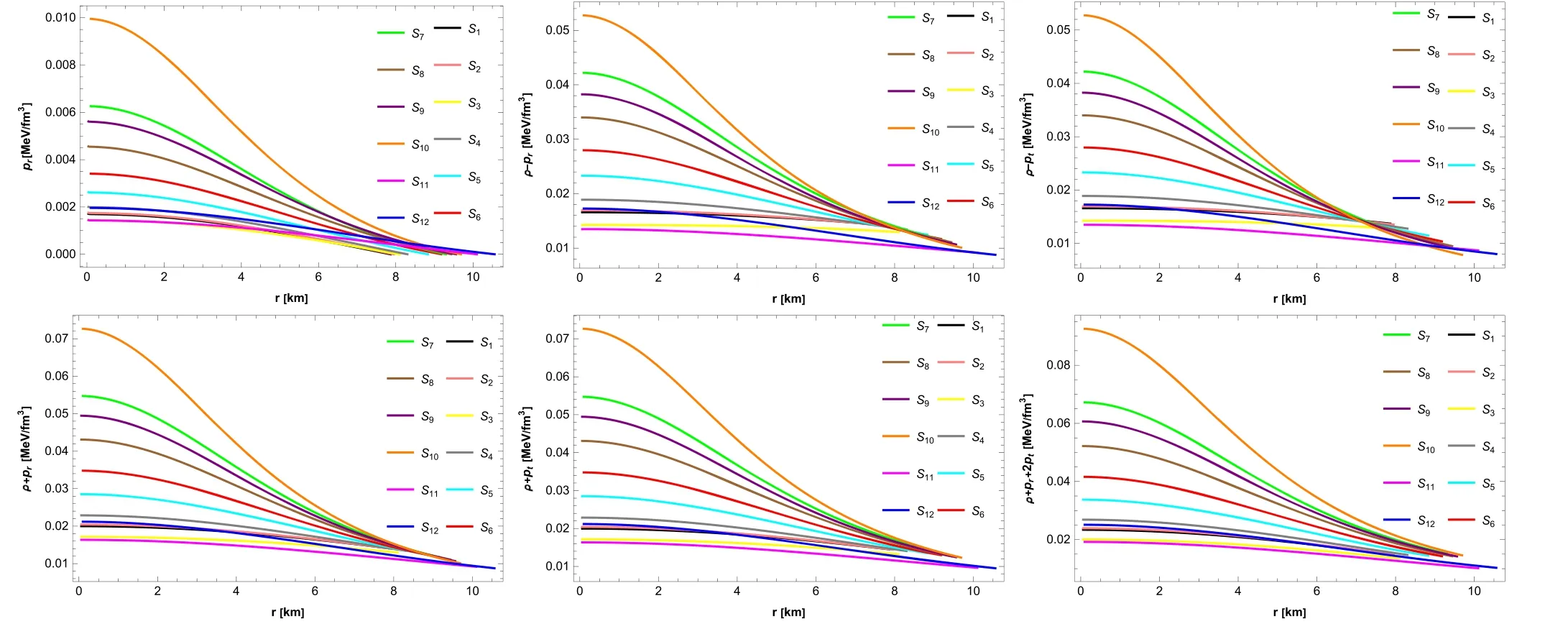
Fig. 2.Graphical variations of ρ,pr and pt for α=0.01,χ=1×107,w0=1,m=1,β=1 for(S1,S2,S3,S4,S5,S7,S8,S10,S11,S12)and β=1.5 for (S6,S9).

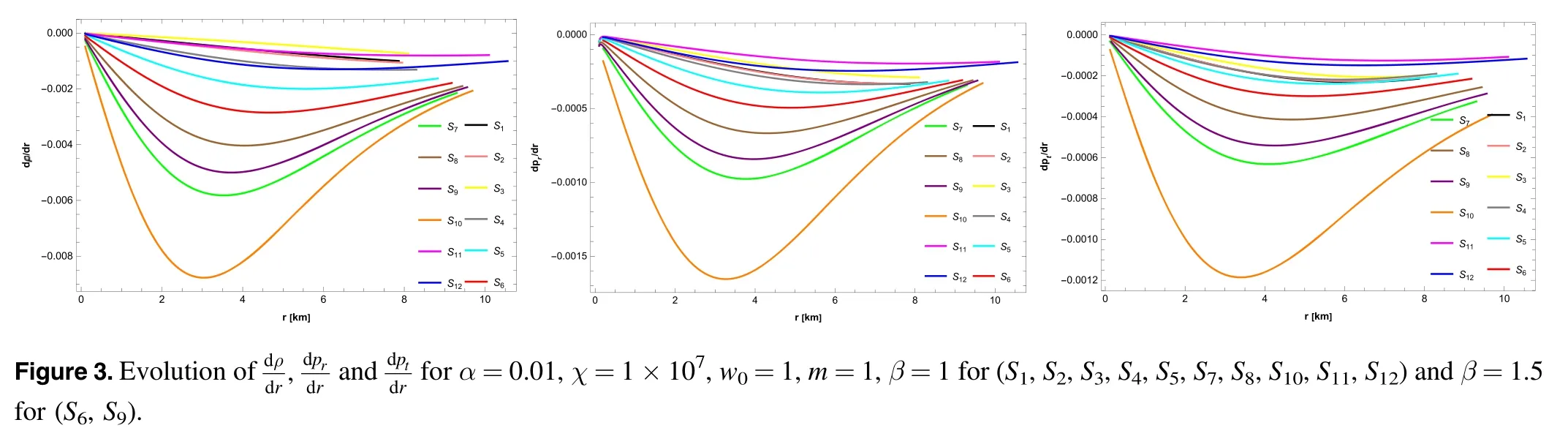
Table 1 contains the constants a,b,A and B for the mass and radius of the selected stellar spheres.Furthermore,it is imperative to emphasize that the following constraints should be met for celestial stars to behave properly:

• The behavior of ρ,prand ptshould be optimistic,continuous,and maxima in the apex.

• Each one of the energy parameters should be accomplished.

• The equilibrium consistency requirement must be met by all of the forces.

4.Physical analysis of f(R,φ) gravity model

Further,we explore the pictorial behavior of the sphere objects under discussion within the light of the f(R,φ)gravity model.We examine various physical investigations,including density,pressure components,mass component,surface redshift,stability,energy and equilibrium conditions.All features are important in describing the characteristics of compact objects.The free parameter β is chosen for the considered stars in such a way i.e.β=1 for(S1,S2,S3,S4,S5,S7,S8,S10,S11,S12) and β=1.5 for (S6,S9).

4.1.Energy density and pressure progression

Here,we examine how the f(R,φ) gravity model affects the graphical representations of the ρ,prand pt.Figure 2 makes it abundantly evident that all graphs represent optimistic behavior.Also,these graphs reach their peak values at the core and contact the surface at the border,demonstrating that they behave comprehensively.

As part of our discussion,figure 3 displays the graphs for the gradients of ρ,prand pt.These attributes reflect the maximum compactness characteristic of astrophysical objects.

4.2.Anisotropy

Here,we explore its graphical response of the anisotropy parameter,defined as Δ=pt-pr[76].Anisotropic factors confirm the validity of stellar objects.Figure 4 shows that the anisotropy component for a given f(R,φ) gravity model demonstrates repulsive behavior when Δ>0.This suggests that our system behaves appropriately and is reliable.

4.3.Tolman-Oppenheimer-Volkoff equation for f(R,T) gravity

Next,we investigate the equilibrium essential of the f(R,φ)gravity model for the ensuing forces: hydrostatics,anisotropic,and gravitational.To accomplish this,we evaluate the TOV equation [44,45] assuming as

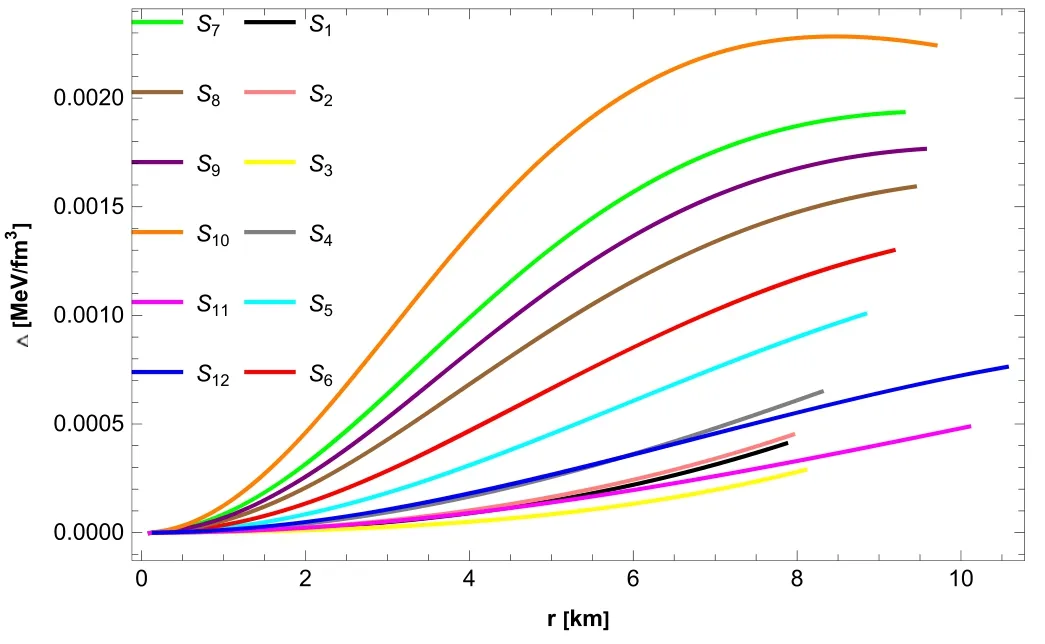
Fig. 4.Evolution of anisotropy for α=0.01,χ=1×107,w0=1,m=1,β=1 for(S1,S2,S3,S4,S5,S7,S8,S10,S11,S12)and β=1.5 for (S6,S9).

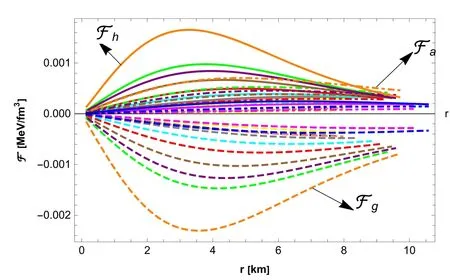
Fig. 5.Behavior ofhF,gF andaF for α=0.01,χ=1×107,w0=1,m=1,β=1 for(S1,S2,S3,S4,S5,S7,S8,S10,S11,S12)and β=1.5 for (S6,S9).

The total sum of the four forces listed above should equal zero for a realistic model of f(R,φ)gravity.It suggests that all of these forces for an equilibrium scenario cancel out each otherʼs effects and preserve the balanced condition,i.e.

The right panel of figure 5 makes it quite explicit that all forces are fulfilled by the appropriate stability criteria.

4.4.Energy conditions

Energy conditions play a major contribution in confirming the validity of compact structures.The following factors comprise the well-known energy conditions: There are four categories of energy:dominant energy conditions(DEC),null energy conditions (NEC),weak energy conditions (WEC),and strong energy conditions(SE)C,defined as

Figure 6 illustrates that all attributes are fully served for the investigated exponential f(R,φ) gravity model.

4.5.Equation of state (EoS) factors

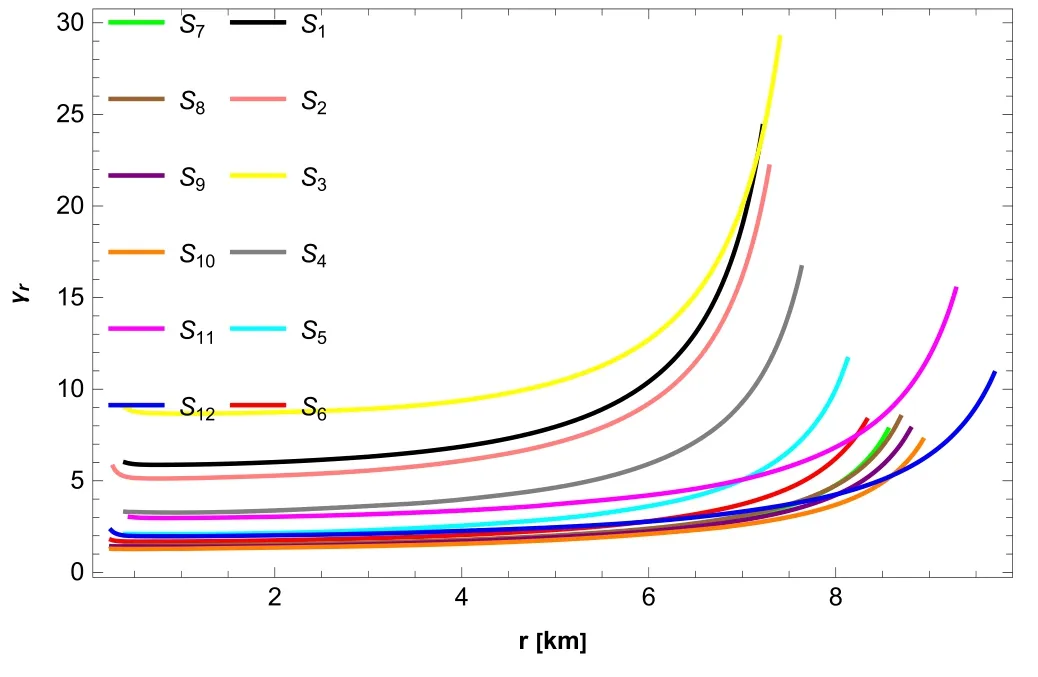
The condition 0

4.6.Mass-radius function,compactness parameter and surface redshift progression

The evolution of the mass distribution demonstrates that mass is constant at the core,i.e.M(r) →0.Also,the mathematical version of the compactness metric U(r)is provided as [79]

The surface redshift function Zs is described as

Fig. 6.Evolution of energy bonds for α=0.01,χ=1×107,w0=1,m=1,β=1 for(S1,S2,S3,S4,S5,S7,S8,S10,S11,S12)and β=1.5 for (S6,S9).

Figure 8 shows a graphical representation of the mass function,compactness parameter,and surface redshift.The plots of these factors show monotonically rising behavior.These graphs confirm the consistent nature of the realistic structures.

4.7.Stability analysis

The stability analysis in the f(R,φ)gravity is discussed in this section.The causality requirement is essential in the topic of stellar spheres.When the f(R,φ) model shows an inner configuration,the sound velocity of the pressure has to be smaller than the speed of the light.The causality element of pressure waves emerges in radial and transverse dimensions in anisotropic systems.All elements should be constrained to the velocity of context to produce an accurate f(R,φ) framework.The following phrase serves as the basis for the stability condition.

4.8.Adiabatic index

We also investigate the stiffness of EoS by examining the adiabatic factor.The adiabatic element value should be higher thanfor a steady structure.The adiabatic parameter proportion is denoted as

Fig. 8.Behavior of M (r),U (r),and Zs for α=0.01,χ=1×107,w0=1,m=1,β=1 for(S1,S2,S3,S4,S5,S7,S8,S10,S11,S12)and β=1.5 for (S6,S9).

Table 2.The numerical values of adiabatic index d critical adiabatic index for the different compact structures.

Our selected exponential f(R,φ) gravity model,as described in figure 10,demonstrates the stable nature of stellar formations.The stability of the model,taking into account the relativistic adiabatic index,requires further analysis due to potential instabilities arising from relativistic corrections to the adiabatic index,denoted as γ [82,83].To address this issue,a more rigorous condition was proposed in[84],which introduces the concept of a critical value,γcrit,for the adiabatic index.This critical value depends on the amplitude of the Lagrangian displacement from equilibrium and the compactness factor U(r) ≡The amplitude of the Lagrangian displacement is characterized by the parameter ζ.A specific form of this parameter allows for the expression of the critical relativistic adiabatic index.

The stability condition for the model is expressed as γ ≥γcrit,as shown in table 2.Notably,the condition γ ≥γcritis consistently met in all cases.Thus,we can confidently assert that the current toy model remains stable when subjected to local radial perturbations induced by relativistic corrections.

4.9.Comparison

Shamir and Malik [85] investigated the behavior of stellar structures in f(R,φ) theory of gravity by using three stars namely Her X-1,SAX J 1808.4-3658,and 4U 1820-30.In our recent work,we have investigated the behavior of stars for twelve different stars,which is more comprehensive analysis than [85].Malik [86] investigated the behavior of charged compact stars in the modified f(R,φ) theory of gravity,by taking four stars like Her X-I,Cen X-III,EXO 1785-248 and LMC X-IV.In our current analysis,we investigated the nature of stellar structures by using the Karmarkar conditions for twelve stars,which makes our work more generalized and comprehensive than the previous investigation.

Fig. 10.Behavior of γ for α=0.01,χ=1×107,w0=1,m=1,β=1 for (S1,S2,S3,S4,S5,S7,S8,S10,S11,S12) and β=1.5 for(S6,S9).

5.Conclusion

• The consistency of ρ,prand ptfor the model under consideration is shown in figure 2.The behavior of these graphs reaches its apex in the core and then declines towards the border.

• Figure 3 illustrates the gradient of ρ,prand pt.These graphs provide non-positive depictions,confirming that our findings are reliable.

• Figure 4 demonstrates that Δ>0,indicating that anisotropic factor is repulsive in nature.This observation confirms the occurrence of astrophysical stars.

• All of the forceshF,gF andaF are steady and display equilibrium manners,as seen in figure 5.

• Figure 6 represents the energy condition for the selected f(R,φ) model.Also,it is worth mentioning that our selected model confirms all of the relevant requirements.

• It is clear from figure 7 that the composition of EoS ratios is uniform.

• Figure 8 clearly shows the monotonically increasing nature of the mass function,compactness parameter,and surface redshift.

• The sound velocity componentsandexist among[0,1]for the exponential f(R,φ)model.Figure 9 shows that the causality conditions are appropriate for the proposed celestial configuration.

• The satisfactory nature of the adiabatic parameter can be noticed in figure 10.

Thus,our research revealed a consistent behavior for all required conditions and well-fitting behavior in the presence of a realistic structure.Also,it is worth saying that our obtained consequences are identical to the conclusions investigated by Asghar et al [62] in the f(R,T) gravity scenario.

Acknowledgments

Adnan Malik acknowledges the Grant No.YS304023912 to support his Postdoctoral Fellowship at Zhejiang Normal University,China.The author,Fatemah Mofarreh,expresses her gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number(PNURSP2023R27),Princess Nourah bint Abdulrahman University,Riyadh,Saudi Arabia.