Gravitational quasinormal modes of a parametrized Schwarzschild metric

Kai Lin and Hongsheng Zhang

1 Hubei Subsurface Multi-scale Imaging Key Laboratory,School of Geophysics and Geomatics,China University of Geosciences,Wuhan 430074,Hubei,China

2 School of Physics and Technology,University of Jinan,336 West Road of Nan Xinzhuang,Jinan 250022,China

Abstract Recently,a parametrized Schwarzschild metric(PSM)was proposed,in which n=2 to solve the differences of mass of M87* from different observations.We find the axial gravitational quasinormal modes of this metric are unstable for n>1.The decay rate of the quasinormal mode of the case n<1 is much smaller than the case n=1,which can be used to differentiate the PSM from a Schwarzschild one.

Keywords: black hole,quasinormal mode,matrix method

1.Introduction

Black holes were one of the most thoroughly studied objects in physics even before their eventual discovery,primarily due to our strong reliance on the principles of general relativity.For many years,astrophysical black holes were cautiously called black hole candidates or x-ray sources.In 2016,the direct observation of gravitational waves (GWs) originating from a binary black hole marked a significant milestone.This compelling evidence not only supported the presence of black holes but also confirmed the validity of general relativity within intense and dynamic gravitational regions [1].Later,the Event Horizon Telescope photographed the super massive black hole in the center of galaxy M87 [2],which presented further evidence for the existence of black holes.At the same time,it also yielded some puzzles.For example,significant discrepancies arise when comparing the results from the different techniques used to measure the mass of M87*.The mass measured using its shadow is about double the mass calculated using the dynamical gases around the hole [3].

Recently,Tian and Zhu presented a parametrized Schwarzschild metric(PSM)to resolve the deviation between different observations,i.e.the dynamical mass and the photo mass[4].There is a parameter n in the PSM and n=1 implies the Schwarzschild metric.We find that a naked singularity appears at the horizon for the case n>1.A naked singularity is a pathological structure of spacetime,where all physical laws lose their predictive capabilities;thus,a conjecture dubbed cosmic censorship has been proposed [5].Several studies have been conducted regarding this conjecture since its initial proposal.Some early studies were devoted to proving that any reasonable initial conditions do not lead to a naked singularity.However,one can find some counter examples since this version is too strong [6].As the cosmic censorship conjecture is pivotal in the framework of gravity theory,one tries to preserve it after some necessary concessions.One finds that the conditions which lead to a naked singularity is a zero measure set in the whole set of initial conditions.Thus,a naked singularity does not actually appear in realistic initial conditions,since a realistic initial condition should be stochastic in a statistical sense[7].Naked singularities are also studied in other research topics;for example,Hawking radiation [8].

For any celestial object,stability is a critical issue because small perturbations from cosmic environments are inevitable.Theoretically,a black hole is the most pure celestial object as it is only determined by three parameters.However,realistic black holes are not pure.They are constantly disturbed by particles and waves from all directions.The stability of black holes was first considered in[9].Generally,the eigen value of the perturbation mode is a complex number.A negative imaginary part of the eigen frequency implies that the mode in consideration is a decay mode,which means that the hole is stable against such a perturbation mode.Such a mode with an imaginary part is called a quasinormal mode (QNM).There have been many investigations of black hole QNMs [10].Here,we study the QNMs of the PSM and find they are unstable for n>1,which is suggested to fill the mass gap between different observations.

In the next section,we derive the axial gravitational perturbation of the background spacetime and investigate the QNM of the PSM in section 3.We find the black hole is unstable under the condition n>1.A brief conclusion is presented in section 4.

2.Axial gravitational perturbation of PSM

In[4],the PSM with a parameter n is proposed to discuss the gravity theory in the strong field region,

In order to analyze the property of this black hole solution,we first focus on the scalar curvature,which is given by

Thus we confirm that a naked singularity appears at the horizon.A naked singularity would destroy the initial problem,leading to a loss of predictive ability in terms of physical theory.With this in mind,we should treat theories with naked singularities very carefully.In fact,n=2 is required to resolve this discrepancy of masses of M87*measured in different observations.Clearly,this case results in a naked singularity at the horizon and it causes the whole theory to be ill-defined.

To investigate mechanical stability of a black hole,the standard method is to explore the QNMs of the hole.We selected the Regge–Wheeler gauge with magnetic quantum number m=0 [11].Under this condition,the metric with axial gravitational perturbation h0(r) and h1(r) is given by

where ω is the QNM frequency andPL(cosθ)is the spherical harmonic function.In appendices B and C,we can prove that the axial gravitational perturbation(or odd model)is given by

where L denotes the angular quantum number.

The tensor perturbation is,in fact,a type of GW.LIGO(The Laser Interferometer Gravitational-Wave Observatory)has detected the GWs from binary black holes [12–14].The waveform of a GW includes three phases: inspiral,merger and ringdown.The ringdown phase carries rich information about the black hole itself,making it a meaningful tool for investigating the properties of binary black holes.It has been found that the ringdown phase of a GW can be described by the waveform from the gravitational perturbation equation of a black hole.In the next section,we study the gravitational QNMs of the PSM.

3.QNMs of the PSM

The ringdown process can be described by QNMs.We consider the wave function of equation(5),which is outgoing at infinity,but ingoing at the horizon.It is difficult to obtain the analytical solution of the QNM master equation,so many numerical methods have been proposed,such as the Wentzel–Kramers–Brillouin (WKB) approximation method [15–17],the finite difference method[18,19],the Horowitz–Hubeny method[20],the asymptotic iteration method [21],the continued fractions method [22,23] and the matrix method [24–27].

In this work,we find that the boundary condition of QNMs depends on the values of the parameter n.For the case of n ≤1,V →0 as r →∞and r=rp,the boundary condition becomes

where x=∫dr/f(r) is the tortoise coordinate.From now on,for the sake of simplicity,we rescale r and ω by r →r/rpand ω →ω/rp.Thus the parameter rpbecomes 1 in the above equation.The QNMs can be dealt with by using many different methods.Here we derive the QNM frequency by a six-order WKB approximation and the finite difference method.

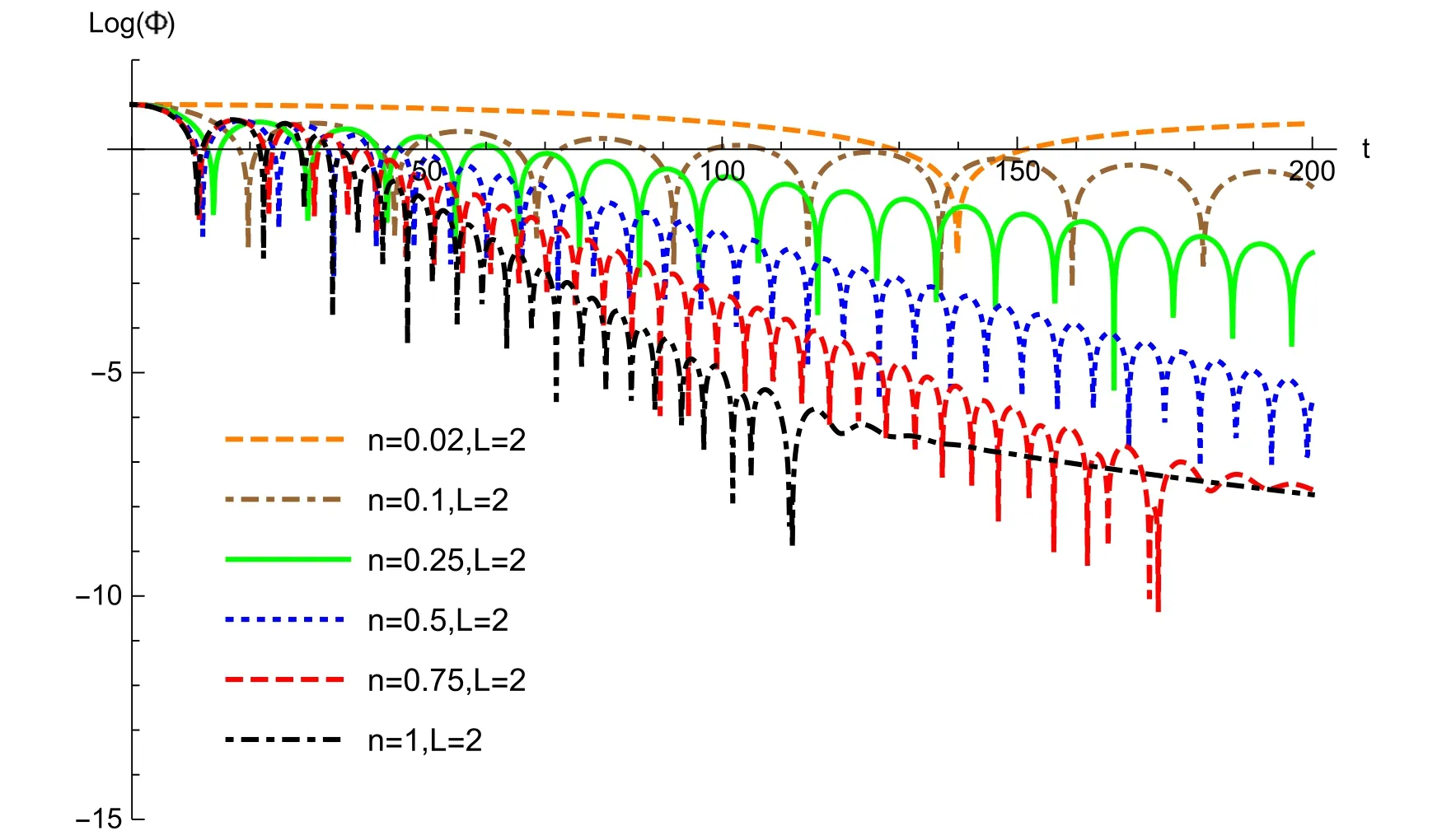
Fig. 1.Quasinormal modes for n=0.02,0.1,0.25,0.5,0.75 and 1.The angular quantum number L=2.

Table 1.The axial QNM frequency by WKB approximation with=0.

Table 1.The axial QNM frequency by WKB approximation with=0.

From table 1,one sees that the imaginary part of the QNM decreases with decrease of n.The modes decay slower and slower with a lower n.The modes of the Schwarzschild case n=1 case) decay faster than any n<1.

Furthermore,we explore the QNMs by the traditional finite difference method,in which the master equation reads

where u=t-x and v=t+x,respectively.Thus,the inverse transformation isx=(v-u).After discretization,we obtain the difference equation

where Δu and Δv are the step lengths in u-and v-directions,respectively.We solve the difference equation with the initial perturbation conditions as follows:

where u0,v0,vcand σ are some parameters,and we set Δu=Δv=0.1,v0=u0=0,vc=3 and σ=1 here.The numerical calculation results are shown in figures 1–3.

From figure 1,it is clear that the QNMs decay slower and slower when n decreases from 1 to 0.The modes of L=3,4 displayed in figures 2 and 3 lead to the same conclusion.Such QNM behavior can be applied to constrain the parameter n in a PSM.

On the other hand,for the n>1 case,V(rp)→-∞and V(∞)=0,which requires that Φ is in outgoing mode at infinity,but vanishes at the horizon,namely

Fig. 2.Quasinormal modes for n=0.02,0.1,0.25,0.5,0.75 and 1.The angular quantum number L=3.

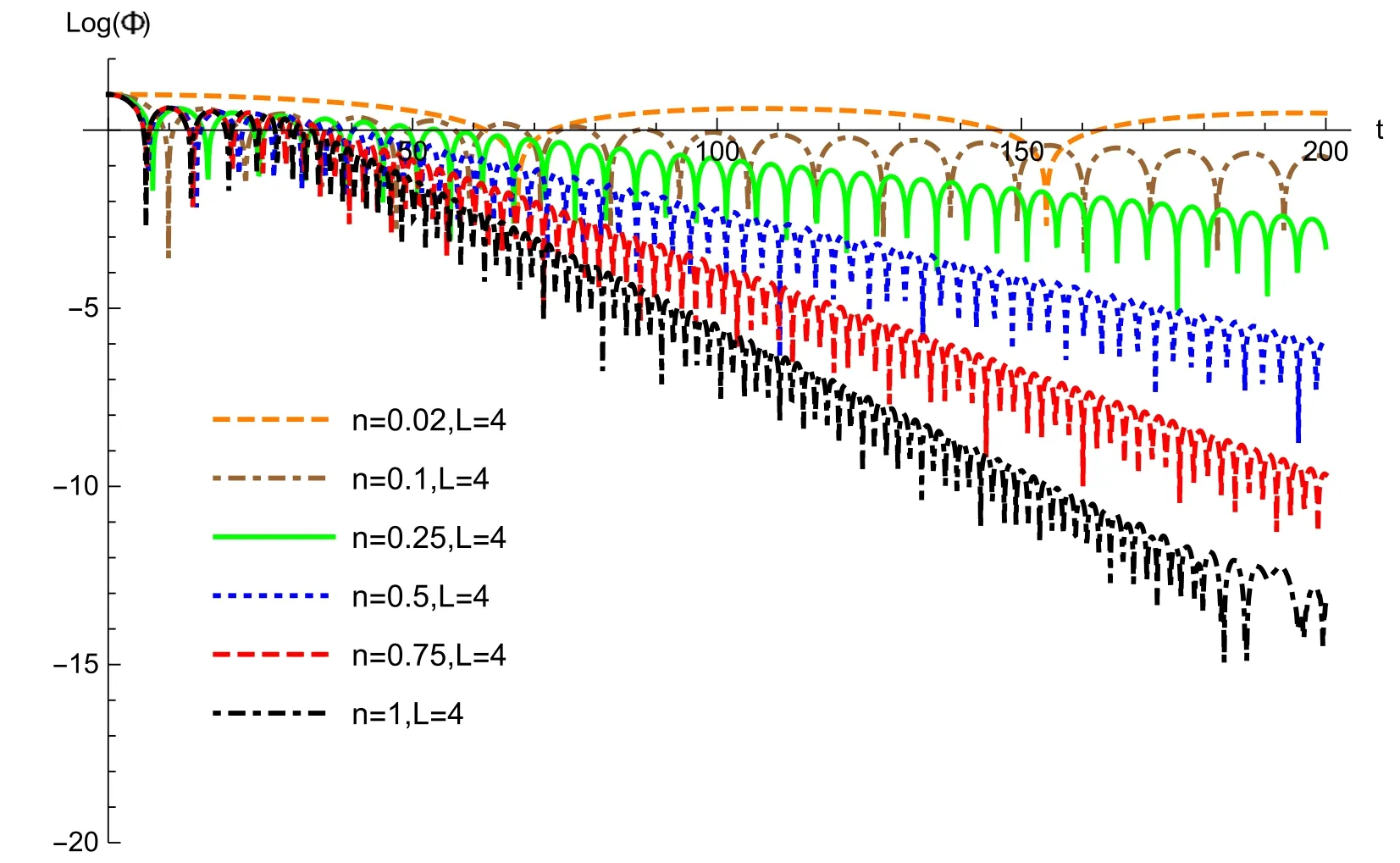
Fig. 3.Quasinormal modes for n=0.02,0.1,0.25,0.5,0.75 and 1.The angular quantum number L=4.

Furthermore,the potential function V(r) with a negative region also implies that the black hole spacetime is not stable under the axial gravitational perturbation.For a non-zero Φ at the horizon,every term of the equation of motion of QNMs(12) becomes divergent at the horizon.Thus this equation does not make sense for a non-zero Φ at the horizon.It is inconvenient to use the u-v coordinate system for finite difference method calculations of QNMs in this case because of the boundary condition at the horizon.Such a boundary condition is very similar to the case of anti-de Sitter (AdS)black hole QNMs.We try to solve the QNMs for the n>1 case following the approach applied in AdS black holes.Now,we rewrite the master equation as

By setting t=t0+iΔt and x=x0+jΔx in equation(12),the finite difference equation becomes

and the initial conditions are chosen as followswhere we set the parameters as t0=0,Δx=2Δt=0.2 CA=0.5,Ca=0.3 and Cb=-1.

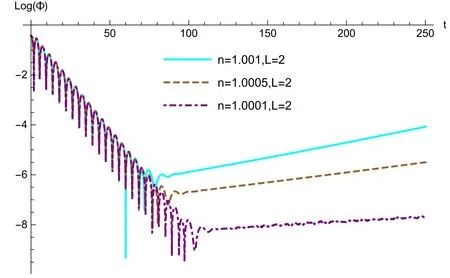
Fig. 4.Instability for n>1 case,where the matrix method with the order n=31 shows that the unstable frequency ω=0.6975+0.0636i with n=1.001,ω=0.6972+0.0637i with n=1.0005 and ω=0.6969+0.0638i with n=1.0001.

Another effective method to calculate the QNMs for the n>1 case is the matrix method[24–27].For this purpose,we set φ=ψexp (iωx) in equation (22),so that the master equation becomes

where Vr=V/f.We find the boundary condition requires Ψ(r)to vanish at horizon rp,while it becomes a constant as r →∞.Introducing the coordinates transformation z=rp/r and ψ ≡zΨ,so that ψ=0 at z=0 and z=1.By using the matrix method,we can numerically calculate the frequency of QNMs and we write down the values in the notes of figure 4.

Figure 4 displays that the late-time tail of the QNM starts to increase with respect to time even for an n that is slightly larger than one.If M87*is described by the PSM with n=2,it is unstable against axial perturbations.

4.Conclusion

A PSM is proposed to explain the mass discrepancy of M87*found from different observations [4].The first observation is dynamical mass,which is derived from the rotation of surrounding gases.The second observation is the recent image of microwaves of the hole.Setting n=2 in the PSM can heal such a discrepancy.We find that the PSM with n=2 is unstable against axial tensor perturbations for the case with n=2.

We calculate the QNMs of the PSM by using WKB approximation and time domain methods,respectively.For the case with n>1,we adopt a matrix method that is used in AdS black holes and find that the PSM is unstable against small perturbations.

For n in the interval n ∊(0,1),the imaginary part of the QNMs of the PSM decreases with a decrease of n.We could apply this property to constrain the parameter n from more and more astrophysical observations.

Acknowledgments

LK is supported by National Natural Science Foundation of China (NNSFC) under contract No.423007 and the Fundamental Research Funds for the Central Universities,China University of Geosciences (Wuhan) with No.G1323523064.HZ is supported by the National Natural Science Foundation of China (NNSFC) under contract Nos.127506 and 123519.

Appendix A.Existence of the PSM in a quintessence-like source model

The work [4] shows that the PSM cannot be realized in vacuum f(R) gravity,while it exists in general relativity with modified electrodynamics.We find that this metric also can be a solution of general relativity with quintessence-like matter.

Quintessence-like matter around a black hole was suggested in [28,29],for which the stress energy reads

where κ ≡8πGnand Gnis the gravitation constant.We show the distribution of ρ(r) in figure 5.

However,it is found that the density is divergent at the horizon.A possible reason is that a particle cannot be in a stable state at the horizon because of the black hole’s strong gravity.However,according to the distribution of density,the total mass of quintessence-like matter is

The result shows that the total mass of this matter is not divergent.It is easy to show that the AdM mass of the PSM metric is nM,which denotes the total mass of the scalar field and gravity field.In the case n=1,i.e.the Schwarzschild case,the total mass is M,which means that we do not need a scalar field.This coincides with our analysis of this spacetime in the main text.

Appendix B.Axial gravitational perturbation equation of the PSM in a quintessence-like source model

For axial perturbation,we set

Substituting the perturbation into the gravitational field equation,we derive the following perturbation equations:

where κ=8πG.Setting h1(r)=rΦ(r)/f(r),we obtain the axial gravitational perturbation equation:

Appendix C.Canceling non-linear electromagnetical terms in the gravitational perturbation equation

If the metric is obtained in non-linear electromagnetic theory,for axial gravitational perturbation,we can generally obtain a master equation as follows:

where δTAis the stress-energy perturbation.In[4],the authors treat the spacetime metric as the solution of non-linear electromagnetic field theory.In this paper,we only consider the perturbation of gravitational field without the perturbation of an electromagnetic field,which means δTA=0.In fact,we can always choose an action to cancel the effect of δTAin perturbation,because the theory does not constrain the form of the non-linear electromagnetic field’s action LEM(I).We demonstrate this point in detail here.

we set I ≡FμνFμνand Fμν≡∇μAν-∇νAμ.As a one-order perturbation field equation can be derived by a two-order perturbation of action,we respectively expand the corresponding quantities as follows:

where the superscript -and 1,2 respectively represent the background quantities and one-and two-order perturbation quantities.Therefore,the action also can be expanded as

Therefore,we set1L and L2as

One sees that the non-linear electromagnetical terms in S2only includes aL¯(I¯)part,which does not contribute to the gravitational perturbation equation.