含孔功能梯度板的动力学分析

娄光路,随岁寒,2*,孟 华

(1.商丘工学院 机械工程学院,河南 商丘 476000;2.苏州聚悦信息科技有限公司,江苏 苏州 215100)

功能梯度材料是一种特殊的多相复合材料,其体积分数在厚度方向上连续变化,因而具有优越的表面性能和机械性能.研究表明功能梯度材料作为涂层和界面区材料,可用于改善接触性能[1-2].功能梯度材料在结构上因其良好的可设计性,在功能梯度梁和杆等应用领域受到了广泛关注[3-5].其中,功能梯度纳米材料在结构中的应用也日益广泛,Yao等[4]研究了功能梯度纳米梁的自由振动问题,Jin等[5]分析了旋转功能梯度压电纳米杆的动力学特性.

同时,板作为经典的二维结构在工程中的应用更加广泛,因此研究板类结构的力学性能十分必要.近年来有部分学者研究了圆形功能梯度板的动力问题[6-7],研究圆板通常基于极坐标建立系统控制方程.更多文献是在笛卡尔坐标系中研究功能梯度方板的力学特性[8-12],这些文献涉及板的自由振动[8-10]、热弹性阻尼[11]及轴向运动条件下的振动特性[12].现有研究较少关注到内部含孔这一条件,事实上,在工程中为避免结构相互干涉或者用于加强固定等目的常常需要在薄板内部开孔,因此需要对带孔板建立相应的力学模型,进而分析其特性.在不包含孔的条件下,板的自由振动问题通常可以采用微分求积法[7]和有限元法[8]来求解.板内部含孔后,微分求积法将不能直接用于求解相关问题.由于有限元法将结构离散为若干单元,分别对各个单元建立单元矩阵,并组装成整体矩阵,进行问题求解.因此有限元法可用于求解含孔功能梯度板的自由振动问题.

假设材料由陶瓷和钢做成,材料特性沿着板的厚度方向按照幂指数形式连续变化.基于Kirchhoff薄板理论,结合虚功原理建立含孔功能梯度板的动力学有限元方程,在四边固支的边界条件下,求解得到系统前两阶固有频率,在纯钢板和纯陶瓷板条件下对比本文解和ANSYS解, 证明所建模型的有效性.

1 控制方程

一个长a宽b厚h的功能梯度矩形板结构如图1所示.

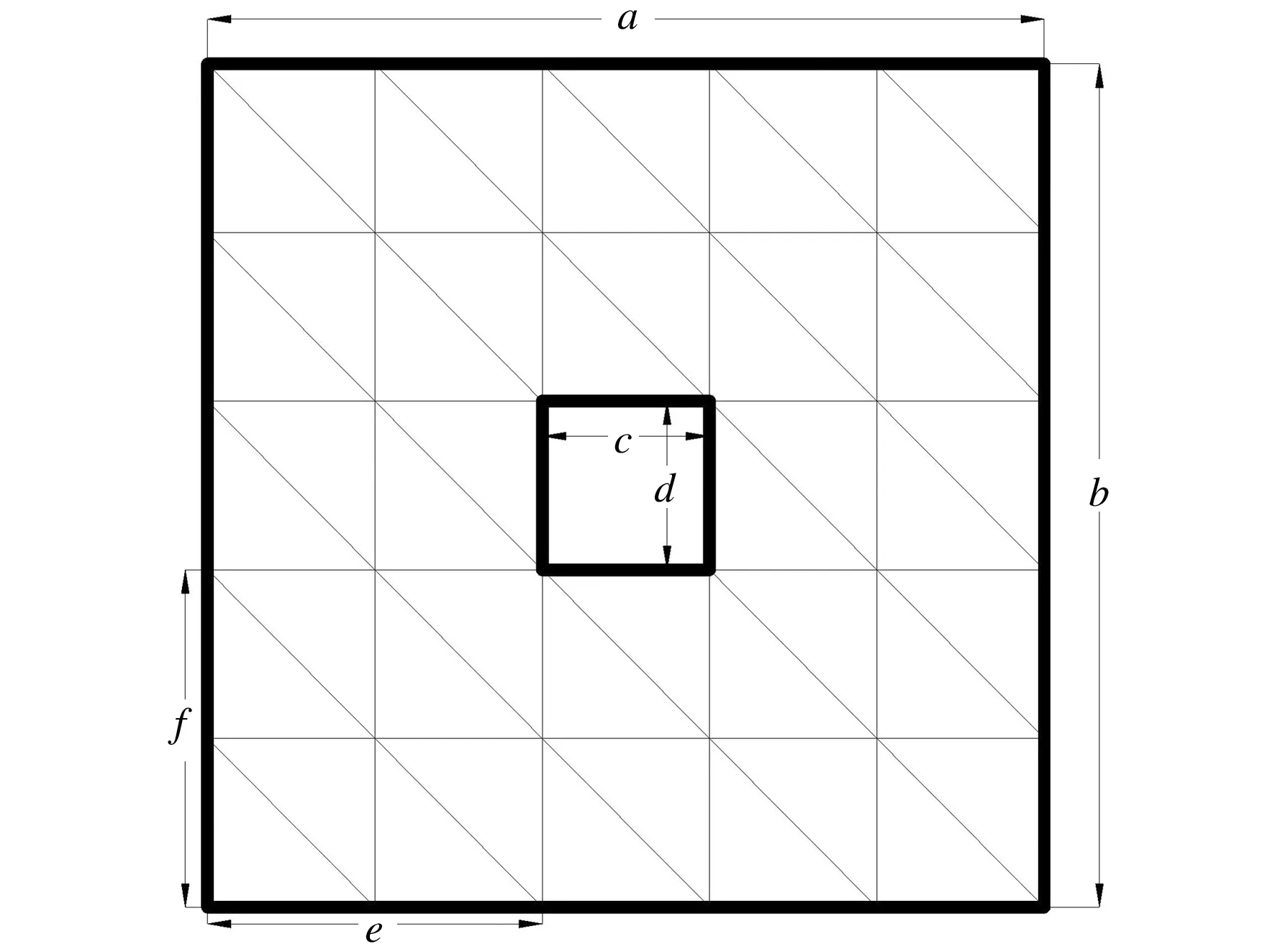
图1 含孔功能梯度板与单元划分结构

孔的长宽分别为c和d,孔距离板边界的距离分别为e和f.功能梯度板由陶瓷和钢复合而成,上表面为陶瓷,下表面为钢,其材料特性符合幂指数形式.功能梯度板的弹性模量E和密度ρ可分别表示为:

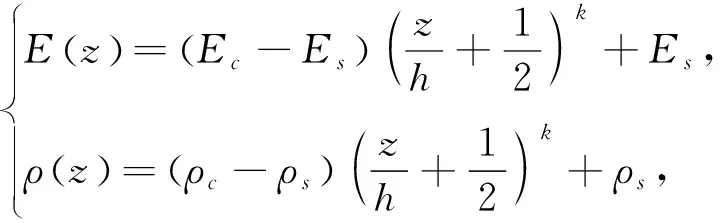
(1)

其中,k(k≥0)表示梯度指数,下标中的c和s分别代表陶瓷和钢.

采用3节点三角形单元,每个节点包含横向挠度以及x和y两个方向的转角,单元的广义坐标为:

(2)

采用广义坐标可将单元的横向位移可表达为:

w=N{d},

(3)

这里N代表形函数.

根据Kirchhoff薄板理论,功能梯度板的位移场为:

(4)

其中u、v分别表示板上任意一点在x和y方向的位移,w表示板中面上的横向位移.惯性力所做虚功为:

(5)

功能梯度板的几何方程为:

(6)

根据式(3)将几何方程整理成矩阵形式为:

ε=[B]{d},

(7)

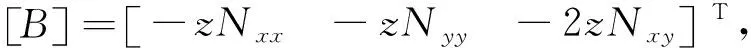
功能梯度板的物理方程为:

(8)

其中μ表示功能梯度板的泊松比,通常取值为0.3.

可以将式(8)简化为:

σ=[D]ε.

(9)

根据式(7)与式(9),功能梯度板的虚应变能表达式为:

(10)

将式(5)和式(10)代入如下虚功原理表达式结果为:

δU=δW.

(11)

可以得到含孔功能梯度板的有限元平衡方程为:

(12)

其中

2 数值算例

式(12)结合四边固支边界条件可得前两阶固有频率,为进行数值分析,功能梯度板的材料性能参数与几何参数如表1所列.

表1 物理参数值

为证明本文所建立有限元模型的有效性,采用ANSYS软件求解前两阶固有频率以及对应的模态函数,纯钢板(n=+∞)的前两阶模态结构如图2所示,纯陶瓷板(n=0)的前两阶模态如图3所示.在ANSYS中采用SHELL281单元,该单元为四边形单元,包含4个角点及4个边的中点共8个节点,每个节点有6个自由度.本文采用图1所示的单元划分,所得解与ANSYS解的对比结果如表2所列,对于纯钢板,本文解误差为0.17%,纯陶瓷板误差为2.06%,可见本文模型在单元数量很少的情况下能够得到比较精确的结果.

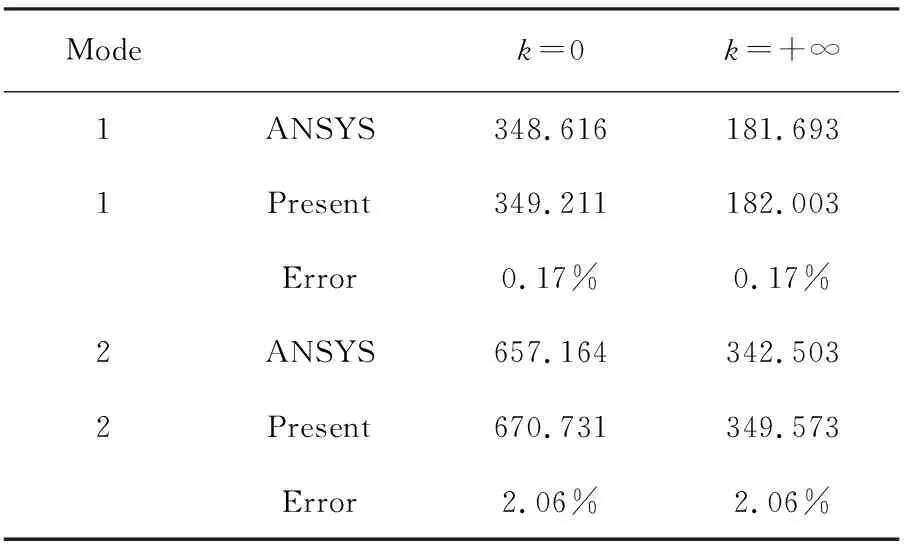
表2 前两阶固有频率对比

图2 纯钢板前两阶振动模态

图3 纯陶瓷板前两阶振动模态

功能梯度材料的最大优势是材料特性可设计,体现可设计的参数为梯度指数,因此有必要探讨梯度指数对自由振动的影响.由于工程中仅关注低阶固有振动,前两阶固有频率随梯度指数的变化情况如图4所示.由图4可见梯度指数增大过程中,前两阶固有频率变化有类似规律,即固有频率先是大幅降低,而后缓慢降低.由式(1)可知,梯度指数变化使得材料的弹性模量和密度相应变化.梯度指数n=0表示板为纯陶瓷;n=+∞表示板为纯钢.陶瓷弹性模量大、密度小;钢的弹性模量小,密度大.因此陶瓷板的固有频率最大,钢板的固有频率最小,且梯度指数越小,其变化对材料属性的影响越大,从而对固有频率的影响较大.根据图4可以推断,随着梯度指数的进一步增大,功能梯度板的前两阶固有频率收敛于钢板的前两阶频率.

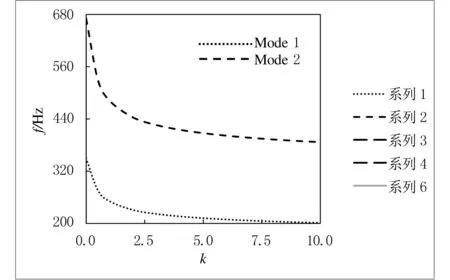
图4 前两阶固有频率与梯度指数关系

3 结论

应用Kirchhoff薄板理论和有限元法研究了含孔功能梯度板的自由振动问题,四边固支条件下通过与ANSYS软件结果对比证明了本文模型的正确性,随后重点分析了梯度指数对前两阶固有频率的影响.结果证实,随着梯度指数增大,前两阶固有频率先急剧降低,而后缓慢降低,最终收敛于纯钢板的前两阶频率.