一种联合修正的稳健Capon波束形成算法
唐佳雨,杨竞舟,胡登辉,张 暘,李大鹏
(1.南京邮电大学 通信与信息工程学院,江苏 南京 210003;2.中国电子科技集团新一代移动通信创新中心,江苏 南京 210019)
0 引言
自适应波束形成(Adaptive Beamforming)是阵列信号处理的一个重要分支[1],它是一种空域滤波技术,可以根据通信环境状况,不断地调整权重矢量,以达到增强期望信号、抑制干扰的目的。
20世纪60年代,Capon在文献[2]中提出了具有高分辨率和高干扰抑制能力的自适应波束形成算法,但该算法在某些情况下输出的SINR会大幅降低。为了提高Capon波束形成算法的稳健性,文献[3-5]提出了对角加载技术,本质是在接收信号的协方差矩阵上加上一个对角阵,等同于扩大了接收信号中噪声的功率。其中,文献[3]通过在样本协方差矩阵中加载一个缩放的特征矩阵,从而提高了算法的稳健性,但是在实际的应用过程中,很难确定加载量的大小。文献[4-5]虽然可以自动选择加载量,快拍数较低时仍能够输出较大的SINR,但在输入信号的信噪比(Signal to Noise Ratio,SNR)较高时,性能会明显下降。
近来又提出了可以提高算法稳健性的导向矢量优化技术。文献[6-9]提出了基于特征空间的优化技术。其中,文献[6]将协方差矩阵特征分解,但是在低SNR的环境下,噪声子空间与信号子空间的特征向量容易发生误判,所以输出性能会急剧恶化。文献[10-13]提出了不确定集约束技术。其中,文献[10]的主要思想是将导向矢量约束在假定的球面或椭球面上,导向矢量可通过求解二次约束二次规划(Quadratic Constrained Quadratic Programming)问题得出。文献[11]为了解决积分带来的运算量问题,将积分区域划分为网格,对每个网格的计算结果进行累加,极大地减小了计算量。文献[12]表明,如果积分的范围越大,则收集的冗余信号越多,在文献[10]的基础上增加了约束条件,使导向矢量被约束在一个不确定集内,将球面积分转化为圆环积分,但减少了一个干扰抑制的自由度。文献[13]由推导出的闭式解,采用图像法确定参数,完成算法的优化求解。
导向矢量优化仅优化了信号来向估计不准的问题,并未考虑协方差矩阵的影响。据此,文献[14-16]提出了协方差矩阵重构的技术。其中,文献[14]提出了基于线性积分的协方差矩阵重构算法,并且给出了积分求解的约束条件。除此以外,文献[16]基于干扰导向矢量和功率估计将干扰信号导向矢量约束在一个不确定集内并通过优化求解得出干扰噪声协方差矩阵。这一方法可以得到稳健的波束形成器,但是计算繁琐,一般需要借助工具包实现。
本文首先构建了一个远场窄带匀直阵列模型,得到了接收天线的接收阵列信号。接着由Capon波束形成算法的最优权矢,分析需要优化的问题。根据问题引出本文提出的联合修正的稳健Capon波束形成算法并进行求解,得到修正后的期望信号导向矢量和干扰噪声协方差矩阵,带入Capon波束形成器即可得到优化后的最优权矢,最后通过仿真验证本文提出的算法性能。
1 系统模型与问题分析
1.1 匀直阵列系统模型
设想一个如图1所示的匀直阵列模型。假设有一个1×N的SIMO信道,且位于远场的发射端有一个期望信号和M个互不相关的干扰信号,它们都是窄带信号,则接收的信号为:
X(t)=AS(t)+n(t)=
(1)
式中:A=[a(θ0),a(θ1),…,a(θM)]为N×(1+M)的导向矢量矩阵,a(θ0)为期望信号导向矢量,a(θ1)、a(θ2)、…、a(θM)为M个干扰信号的导向矢量,其中a(θk)=[1,ejβk,…,ej(N-1)βk],βk=2πdsinθk/λ,λ为波长,d为阵元间距,S(t)为期望信号与干扰信号的复包络,n(t)为N×1的噪声向量。
1.2 Capon波束形成技术
根据接收信号X(t),可以得到接收信号的协方差矩阵为:
R=E[X(t)XH(t)]=
(2)
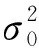
式(2)中:
(3)
(4)
式中:Rs、Ri+n分别表示期望信号协方差矩阵和干扰加噪声协方差矩阵。
接收信号协方差矩阵可通过下式计算得到:
(5)
式中:K表示快拍数,X(k)表示第k个快拍的接收信号。
Capon波束形成器原理是通过在将信号来向的响应设置为常量的约束条件下,选择能将阵列接收到的信号的功率最小的权矢[17]。所以,标准Capon波束形成的权重矢量为:
(6)
式中:P为Capon波束形成器的功率谱。
1.3 问题分析
在应用过程中,一般使用谱估计的方法得到信号的入射角度,进而得到导向矢量,这会产生导向矢量失配的问题,即由于信号入射的角度估算偏差而导致的导向矢量误差。对导向矢量估计不准,就会使输出的SINR降低。
在SNR较高时,由于期望信号功率较高,接收信号协方差矩阵中包含期望信号,根据式(6)可知,此时输出SINR将急剧降低。如图2所示,期望信号方向为0°,干扰信号为-27°和45°,当协方差矩阵中含有期望信号时,期望信号0°位置也产生了零陷。

图2 协方差矩阵中含有期望信号的方向图Fig.2 Directional patterns containing expected signals in the covariance matrix
近来,围绕Capon算法的优化,都基于这两个问题开展。但现有的很多算法的灵活性和稳健性都不够高。
本文提出一种联合修正的稳健Capon波束形成(Joint Modified Robust Capon,JMRC)算法,首先将接收信号协方差矩阵特征分解为信号空间和噪声空间,基于导向矢量与噪声空间的正交性,使期望信号导向矢量在噪声子空间的投影最优,对估计的期望信号导向矢量进行修正。该算法采用拉格朗日乘子法求解,可通过动态调节约束参数,达到在不同通信环境下都能在期望信号方向上获得最大输出响应的目的。再基于对残余噪声消除和对干扰功率的估计,对期望信号协方差矩阵特征分解,并由此得到投影矩阵,消除接收信号中的期望信号,修正协方差矩阵。将结果带入即可得到修正后的Capon最优权矢。该算法可以很大程度上解决现有很多算法稳健性和灵活性不足的问题。
2 联合修正的稳健Capon波束形成算法(JMRC)
JMRC算法包含两部分:导向矢量修正和干扰噪声协方差矩阵重构。
2.1 导向矢量修正
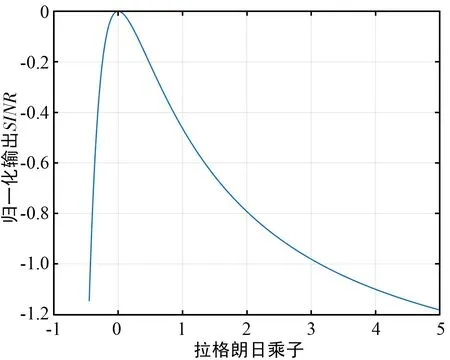
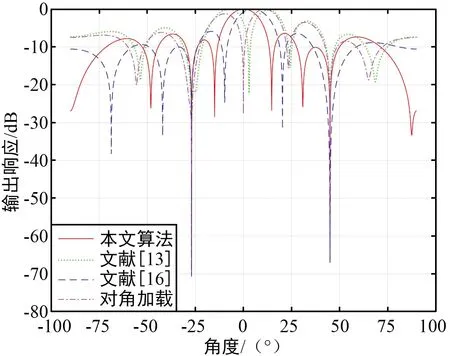
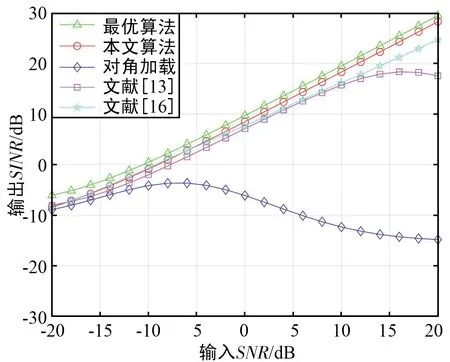
假设期望信号个数与干扰信号个数之和小于阵列天线数,即1+M (7) 对于协方差矩阵R,右乘En可得: (8) 而由式(2)可得: (9) 式中:A=Span{a(θ0),a(θ1),…,a(θM+1),…,a(θN)}为导向矢量张成的矩阵空间。 由式(8)和式(9)可得: ARsAHEn=0, (10) (AHEn)HRs(AHEn)=0。 (11) 式(11)成立的充要条件为AHEn=0,即: (12) 可改写为: (13) 式中:‖·‖2为矩阵-2范数。 (14) 由于其最小值一定取在约束条件的边界上,对于式(14)的求解可使用拉格朗日乘子法。所以构造如下拉格朗日函数: (15) 式中:λ为拉格朗日乘子。式(15)中,对a0求偏导可得: (16) 令式(16)等于0得: (17) 带入约束条件可得: (18) (19) 对式(19)求逆: (20) 带入式(18)可得: (21) (22) 解出λ为: (23) 结合式(17)~式(23)的结果可以得解出修正后的期望信号导向矢量a0。 设有一个功率为σ2的信号从δ角度入射,此时接收信号的协方差矩阵为: (24) 由式(6)可知此时的功率谱为: (25) 在实际过程中残余噪声可以用式(26)求得: (26) 式中:K为采样点数,θ∈Θ且Θ为除期望信号与干扰信号所在角度外的区域,θk为角度区域上第k个采样点。 由式(24)~式(26)可得实际噪声功率与噪声协方差矩阵为: (27) 残余噪声会影响协方差矩阵重构的稳健性。可以在消除残余噪声后对功率谱在期望信号角度区域内积分求得期望信号协方差矩阵,即: (28) (29) (30) 图3 与子空间的正交性Fig.3 QHXi(k)+QHXn(k),i(k)+QHXn(k), (31) 带入式(31): (32) 而: (33) (34) 式中:Θi为干扰信号所在角度区域。则修正后的干扰噪声协方差矩阵为: (35) 综合前文,本文JMRC算法步骤如下: 步骤1对接收信号协方差矩阵特征分解,由式(7)得到噪声特征向量并由此张成噪声子空间En。 步骤2基于En对期望信号导向矢量修正。选定约束参数ε,结合求得的pl,由式(23)计算出拉格朗日乘子λ的值。将λ的值带入式(17)即可得到修正后的导向矢量a0。 步骤3由式(29)对消除残余噪声后的期望信号协方差矩阵特征分解。选定参数J,得到子空间B1。 (36) 为了验证本文JMRC算法的性能,选取最优算法、文献[13,16]对角加载与本文提出算法进行对比,其中最优算法指导向矢量不存在失配且协方差矩阵中不含期望信号的Capon算法。设阵元个数N=8,阵元为间距为半波长的匀直阵列(Uniform Linear Array,ULA)。快拍数为K=512。为仿真方便,本文假设有一个来自0°的期望信号和两个分别来自-27°、45°的干扰信号。两个干扰信号的功率均为30 dBm,各个信道噪声是功率为0 dBm互不相关的高斯白噪声。假设存在5°的角度失配,即期望信号来向被估为5°。 输出SINR与拉格朗日乘子的关系如图4所示,由图可知,拉格朗日乘子λ的值接近0时的归一化输出SINR近乎最大。拉格朗日乘子与约束参数的关系如图5所示,若拉格朗日乘子的值近似于0,此时的约束参数ε的值约为2.5。故为了获取最佳性能,本次仿真的ε=2.5。 图4 输出SINR与拉格朗日乘子的关系Fig.4 Relationship between output SINR and Lagrange multiplier 图5 拉格朗日乘子与约束参数的关系Fig.5 Relationship between Lagrange multiplier and constraint parameter 图6给出了各算法的方向增益图,可以看出,本文的优化算法不仅在干扰方向-27°、45°上形成了很深的零陷,而且在期望信号0°方向获得了最大归一化输出SINR。其他算法虽然也在干扰方向上形成了零陷,但是文献[13]与对角加载技术在期望信号方向上也形成了较深的零陷,说明此时接收到的协方差矩阵中包含大量期望信号。文献[16]相较于上述两个算法性能有了很大提升,但是输出SINR与本文JMRC算法相比还存在一定差距。 图6 各算法方向图Fig.6 Directional diagram of each algorithm 图7给出了输出SINR与输入SNR变化的关系,可以看出,在SNR很低时,仿真的5种算法输出SINR都呈递增趋势,但对角加载技术由于未对导向矢量进行优化,输出SINR最低,且在-5 dB左右位置对角加载技术的输出SINR开始急剧下降,这是因为协方差矩阵中已包含了大量的期望信号。在10 dB附近,文献[13]算法输出SINR也出现了下降趋势。而本文JMRC算法呈一条直线,未出现输出SINR下降的情况,且在SNR较高时,相较文献[16],输出SINR也有较高的提升。 图7 输出信号SINR与输入SNR的关系Fig.7 Relationship between output signal SINR and input SNR 图8给出了输出SINR与导向矢量失配角度的关系,可以看出,当不存在导向矢量失配的问题时,5种算法的输出SINR大体一致。当角度误差增大时,对角加载技术、文献[13]和文献[16]算法的输出SINR明显降低,而本文JMRC算法输出SINR降低的幅度较小。 图8 输出SINR与导向矢量失配角度的关系Fig.8 Relationship between output SINR and steering vector mismatch angle 图9给出了输出SINR与快拍数的关系,可以看出,除对角加载技术与文献[13]算法外,其他算法对于快拍数K的变化并不敏感。对于本文JMRC算法而言,其与最优算法几乎有相同的输出SINR,且性能优于其他算法。 图10给出了SNR=20 dB下的输出SINR与干扰个数的关系,可以看出,本文JMRC算法、文献[16]算法对于干扰个数并不敏感,但本文算法对干扰个数的容忍程度大于文献[16],且输出SINR与最优算法相比并无较大差异。而对角加载技术和文献[13]算法的输出SINR显著降低。 图10 输出SINR与干扰个数的关系Fig.10 Relationship between output SINR and the number of interferences 在算法复杂度方面,文献[13,16]在求解时需要解决的凸优化问题复杂度高,一般需要使用CVX工具包实现。而本文算法主要使用特征分解求解,复杂度低且系统可以复用这一结构,减小了系统的额外开销。 本文首先对导向矢量进行修正。优化求解采用了拉格朗日乘子法,因为约束参数ε与拉格朗日乘子λ的关系,所以可以动态调节ε的取值而获得最大的输出SINR,具有较高的灵活性。选取ε=2.5即可得到最大的输出SINR,解决了导向矢量失配导致输出SINR降低的问题。然后对协方差矩阵进行修正,利用构造的投影矩阵Q对期望信号消除后再对干扰功率积分得到修正后的协方差矩阵,解决了协方差矩阵中存在期望信号而导致的期望信号方向产生零陷的问题。仿真结果表明,本文JMRC算法的输出SINR不会因为输入SNR增大而减小,且对于导向矢量失配角度、快拍数、干扰个数的变化不敏感。在通信质量较差的环境下仍然能够获得较高的输出SINR,稳健性高。但JMRC算法要求各个干扰信号之间相互独立,且入射信号需为远场窄带信号。因此,在未来的工作中,需要进一步研究适用于相干干扰、近场非平面波的稳健算法。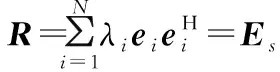



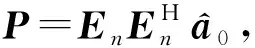
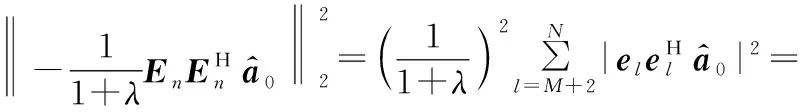
2.2 干扰噪声协方差矩阵修正
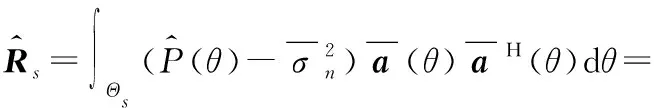
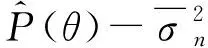
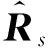


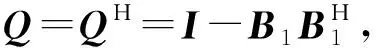


2.3 算法流程
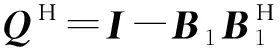
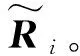
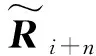
3 仿真分析



4 结论

