基于FPGA的Multi-h CPM高速解调系统设计与实现

刘誉楷,刘荣科,2*,陈祺治

(1.北京航空航天大学 电子信息工程学院,北京 100191;2.深圳北航新兴产业技术研究院,广东 深圳 518063)

0 引言

卫星互联网技术可以利用卫星信道连接全球范围内的用户,在现代通信系统中发挥了至关重要的作用。它不仅能够提供高速稳定的接入服务,且不受地理和地形的限制,可以满足各种应用需求,在电信、航天等各个领域都有着广泛的应用前景[1-3]。

在卫星通信系统中,信号调制与解调是实现高速数据传输的关键技术之一[4]。连续相位调制(Continuous Phase Modulation,CPM)技术通过控制信号的相位变化来调制信号,相较于其他的数字调制技术,CPM可以在较低误码率下提供更高的频谱效率[5]。此外CPM具有恒包络的特点,可以有效降低高功率放大器非线性效应的影响[6],适合应用于卫星等功放受限的场景。

多指数连续相位调制(Multi-h Continuous Phase Modulation,Multi-h CPM)是CPM的一种扩展形式。Multi-h CPM通过采用不同的调制指数,改变调制信号的相位偏移量。与传统的CPM技术相比,Multi-h CPM可以通过选择不同的调制指数来适应不同的信道环境,提高数据的传输效率,改善系统的容错性能[7]。

目前Multi-h CPM接收机中最常采用的算法是最大似然序列检测(Maximum Likelihood Sequence Detection,MLSD)算法[8]。但是由于Multi-h CPM相比于CPM信号,其解调的复杂度较高,还需要采用一些简化算法来降低算法的复杂度。降低Multi-h CPM的解调复杂度有两个主要方向:降低匹配滤波器数量和减少网格状态数。降低匹配滤波器数量的简化算法主要包括脉冲幅度调制(Pulse Amplitude Modulation,PAM)分解[9-10]、Walsh分解[11]、奇异值分解(Singular Value Decomposition,SVD)[12]、状态空间分类(State Space Partitioning,SSP)算法[13]和虚拟指数集解调算法[14]等。降低网格状态数的简化算法主要包括倾斜相位(Tilted Phase,TP)算法[15]、频率脉冲截断(Frequency Pulse Truncation,FPT)算法[16]和减状态序列检测(Reduced State Sequence Detection,RSSD)算法[17]等。以上算法中,除了TP算法之外,其他算法都会降低接收机的解调性能。在实际的系统设计时,通常将几种降低复杂度的算法联合应用,通过牺牲部分解调性能的方式,显著降低接收机系统的实现复杂度。

为了实现高效的Multi-h CPM解调,保证接收机的高速数据处理能力,除了降低解调算法的计算复杂度之外,还需要在硬件架构设计时,通过高度并行化的数据处理方案,提高系统的吞吐率。

现场可编程门阵列(Field Programmable Gate Array,FPGA)作为一种可编程的逻辑器件,具有可重构性强、高并发性能、高速运算能力、低功耗和灵活性等优点,可以支持多个逻辑电路并行计算,进行复杂的逻辑电路设计与实现,在信号处理和通信领域得到了广泛应用[18]。

因此本文设计并实现了基于FPGA平台下的Multi-h CPM解调系统,完成了Multi-h CPM的软输出维特比算法(Soft Output Viterbi Algorithm,SOVA)[19-20]、时频同步等功能,并且采用了TP算法和FPT算法,大幅度降低了系统的解调复杂度。通过仿真和实验验证,本文的Multi-h CPM接收机具有良好的系统性能,可有效满足实际应用需求。

1 Multi-h CPM系统模型

1.1 Multi-h CPM

Multi-h CPM的复基带信号可以表示为:

(1)

式中:ES为信号能量,T为码元周期,φ(t;a)为信号相位,其可以进一步表示为:

(2)

式中:ai∈{±1,±3,…,±(M-1)}为传输的M进制符号序列,hi∈{h1,h2,…,hn}为调制指数集,q(t)为相位脉冲响应,可以表示为频率脉冲响应g(t)的积分,即:

(3)

目前Multi-h CPM调制中最常用的脉冲函数为升余弦脉冲,其表达式为:

(4)

式中:L为关联长度。当L=1时,生成的Multi-h CPM信号为全响应信号;当L>1时,生成的信号为部分响应信号。

1.2 Multi-h CPM相位网格状态

Multi-h CPM信号在确定了调制参数的情况下,信号相位φ(t;a)仅与累加相位和关联长度内的传输符号有关,因此式(2)可以改写为:

(5)

式中:φn为累加相位,φ(t;a)为相关相位。

考虑到调制指数hi为有理数,因此Multi-h CPM信号的累加相位状态是有限的。令hi=m/k,其中m和k是互斥的两个质数,则累加相位的所有状态集合为:

(6)

综合考虑累加相位和相关相位的影响,Multi-h CPM信号的相位可以由下述状态序列决定:

sn={an-L+1,an-L+2,…,an-1,φn-L}。

(7)

相位状态转移的表达式为:

(8)

假设Multi-h CPM的调制进制数M=2,关联长度L=1,调制指数h={1/4,1/2},其相位状态转移如图1所示。从状态转移图中可以看到,Multi-h CPM的信号相位具有周期性的网格结构,根据网格图的转移关系可以清楚地描述当前的信号状态和下一码元对输出信号的影响。

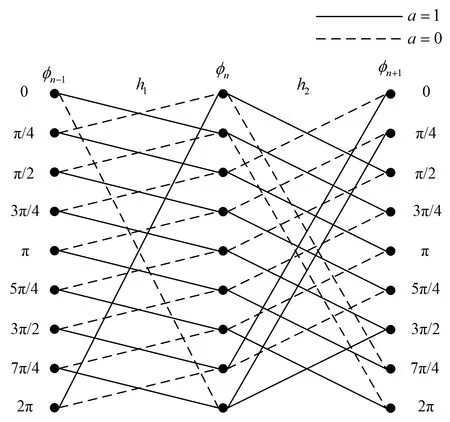
图1 Multi-h CPM相位状态转移图Fig.1 Phase state transition in Multi-h CPM system

在Multi-h CPM中,进制数M将会影响到状态转移的复杂程度。当M=2时,每个状态有两条转移路径,而当M=4时,每个状态有4条转移路径。而进制数M、关联长度L和调制指数h共同决定了网格状态数,随着Multi-h CPM调制进制数的提升和关联长度的提升,都会导致整个系统的状态数呈指数增长,进而导致解调的复杂度上升。

2 Multi-h CPM解调算法

2.1 Viterbi解调算法

假设信道为加性高斯白噪声信道(Additive white Gaussian Noise,AWGN),接收信号r(t)可以表示为:

r(t)=s(t;a)+n0(t),

(9)

式中:n0(t)为零均值高斯白噪声。

根据MLSD准则,接收机在所有可能的结果中搜索距离接收信号的欧氏距离最近的一组序列值作为检测结果,该检测器可以表示为:

(10)

MLSD的目标是通过求解似然函数来在所有可能序列中寻找使式(10)最小的序列。考虑到Multi-h CPM信号的恒包络特点,计算式(10)的最小值可以等价为计算式(11)的最大值。

(11)

由于Multi-h CPM信号具有相位网格特性,可以使用Viterbi算法完成信号解调工作。Viterbi算法中状态转移的度量值计算公式为:

(12)

整个Viterbi算法包括了分支度量计算、路径度量值更新、路径选择和路径回溯等几个步骤。分支度量计算通过计算接收信号和每个不同的符号序列下的相关值,获得不同状态下的不同路径度量值。路径度量值更新是将计算得到的分支度量与上一时刻对应状态下的累计度量值进行累加,获得当前时刻下的所有路径的累计度量值。路径选择是对比每个状态下所有路径的累计度量值,选择最大路径的度量值结果作为新的累计度量值。重复上述步骤,从而完成整个序列的搜索过程。路径回溯是选择度量值最大的状态,沿着度量值更新的路径进行路径回溯,最终实现Multi-h CPM的信号解调。

2.2 软输出Viterbi算法

由于传统的Viterbi算法在进行路径回溯后,只能获取符号序列的硬判决结果,而在通信系统中,解调器之后一般会级联译码器。考虑到译码器的纠错性能,译码器输入软信息相比于硬判决结果,可以获得更大的编码增益。在Multi-h CPM接收机解调时,为了能够给后级的译码器提供软信息,因此采用了软输出Viterbi算法。

图2中实线为t-6～t时刻最大累计度量值的回溯路径,即幸存路径。虚线为t-6～t时刻次大累计度量值的回溯路径,即竞争路径。节点Si在t时刻下的可靠性度量值Δt(Si)可以表示为幸存路径下的累计度量值和竞争路径下的累计度量值之差,即:

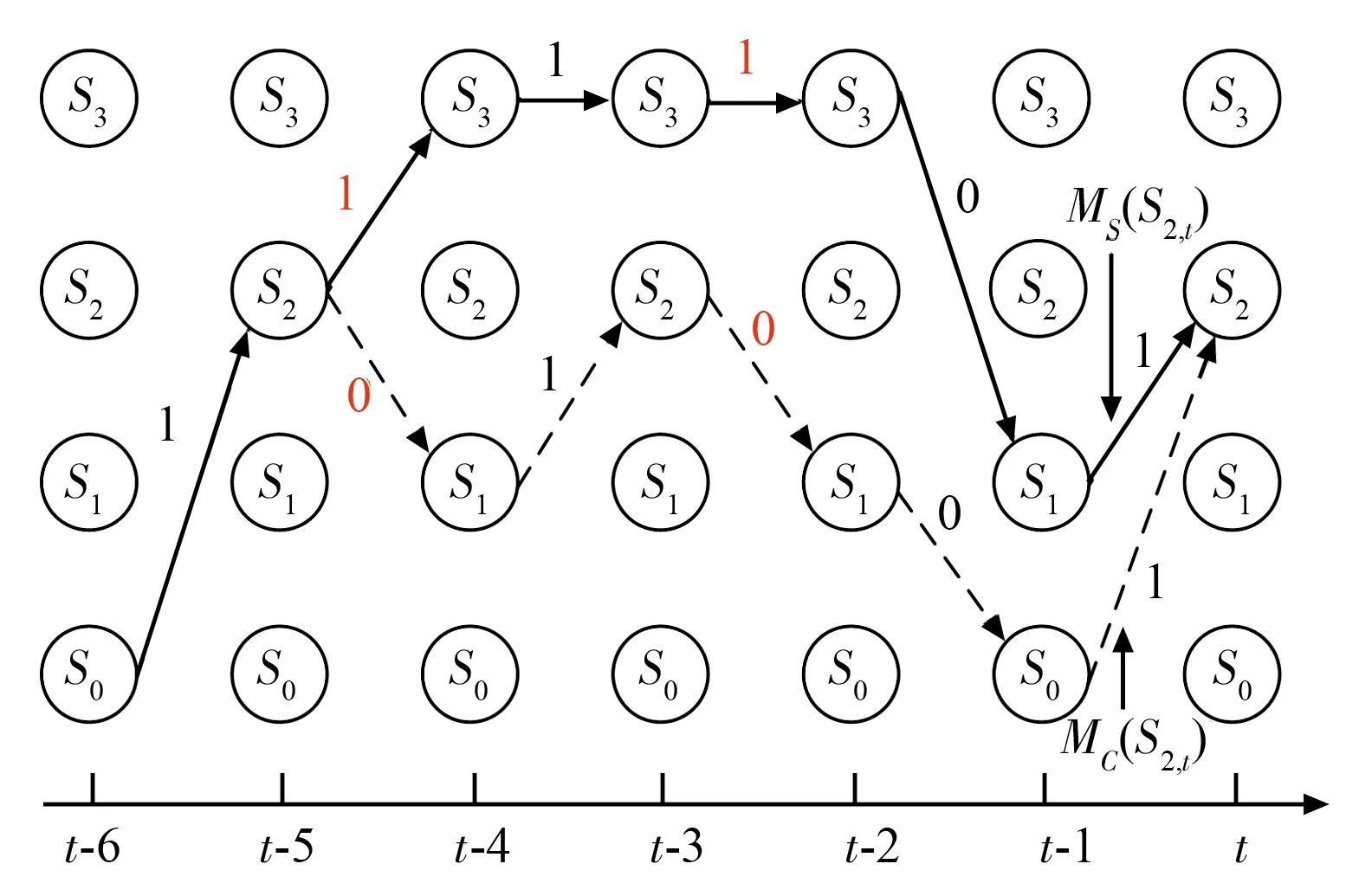
图2 幸存路径和竞争路径网格图Fig.2 Trellis diagram of survivor path and competing path

Δt(Si)=|MS(Si,t)-MC(Si,t)|。

(13)

由图2可以看出,幸存路径和竞争路径在t-5时刻开始分离,并且幸存路径和竞争路径的比特判决结果并不是完全相同。在t-4和t-2时刻,幸存路径的比特判决结果是1,竞争路径的比特判决结果是0。因此仅通过t时刻幸存路径和竞争路径下的度量值之差,不能完全表征可靠性度量值,还需要考虑幸存路径和竞争路径的比特判决结果,对可靠性度量值进行修正。

对于t时刻下的状态节点Si,可靠性度量值的更新算法计算过程如下:

① 存储节点Si的可靠性度量值Δt(Si),如果竞争路径不唯一,计算幸存路径和所有竞争路径的度量值之差,并将最小值存储到Δt(Si)。

② 将状态节点Si的可靠性数值初始化为+∞。

③ 比较状态节点Si下的幸存路径与竞争路径的判决结果,并计算判决结果不同的时刻与节点所在时刻下的差值,将结果记录到MEM。

④ 在所有的MEM>0的时刻中,找到可靠性数值未更新过的最小的MEM,记为MEMlow。

⑤ 将MEM=0到MEM=MEMlow时刻之间,可靠性最小的数值更新为MEMlow的可靠性。

通过可靠性更新算法之后,可以获得状态节点Si的可靠性度量值。结合路径回溯的硬判决结果与状态节点的可靠性数值,就可以得到译码器所需要的软信息结果。

2.3 Multi-h CPM降复杂度算法

2.3.1 倾斜相位算法

倾斜相位算法可以通过引入参考相位的手段将相位树从时变转化为非时变的形式,并且在无性能损失的前提下可以实现网格状态数减半。

在式(2)中,φ(t;a)的相位定义在实数域上,而考虑真实的物理相位,相位差为2π整数倍的相位是不能被区分的,所以对φ(t;a)进行如下处理:

(14)

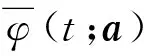
在Multi-h CPM中,信号的相位转移既与传输的信息有关,也与当前时刻有关,增加了信号解调的复杂度。为了解决此问题,使用单极性符号Un取代双极性符号an,其转换公式为:

(15)

使用单极性符号后,令第n个符号间隔内的时间t=τ+nT,信号相位可以重新表示为:

(16)

对式(16)的相位进行模2π,可以得到:

(17)

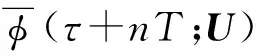
(18)

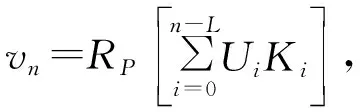
(19)

没有进行符号映射前,Multi-h CPM的信号相位是模2P。通过TP算法对信号的相位坐标系进行转换后,信号相位从模2P变成了模P。在进行Viterbi解调时,相位状态数降低为原来的1/2,可以有效地降低Viterbi解调的计算复杂度。由于TP算法只是通过坐标系变换重新映射了信号相位,因此不会影响到Multi-h CPM接收机的系统性能。

2.3.2 频率脉冲响应截断算法

针对部分响应Multi-h CPM信号,可以采用频率脉冲响应截断算法降低系统的计算复杂度。对于部分响应信号的CPM信号,由于其频率脉冲两端的幅度较小,对信号相位的影响可以忽略,因此考虑对频率脉冲响应曲线进行截断,去掉低能量部分,等效的降低了信号的相关长度L。

假设Multi-h CPM的调制参数M=4,L=3,h={5/16,6/16},其 FPT算法截断方式如图3所示。Multi-h CPM信号的频率脉冲响应函数在0T～0.5T和2.5T～3T这两个区间取值设置为0。由于其0.5T～2.5T区间内的能量占据了总能量的95%左右,因此通过截取频率脉冲响应,可以在仅损失少量信号能量的同时,有效降低响应长度。

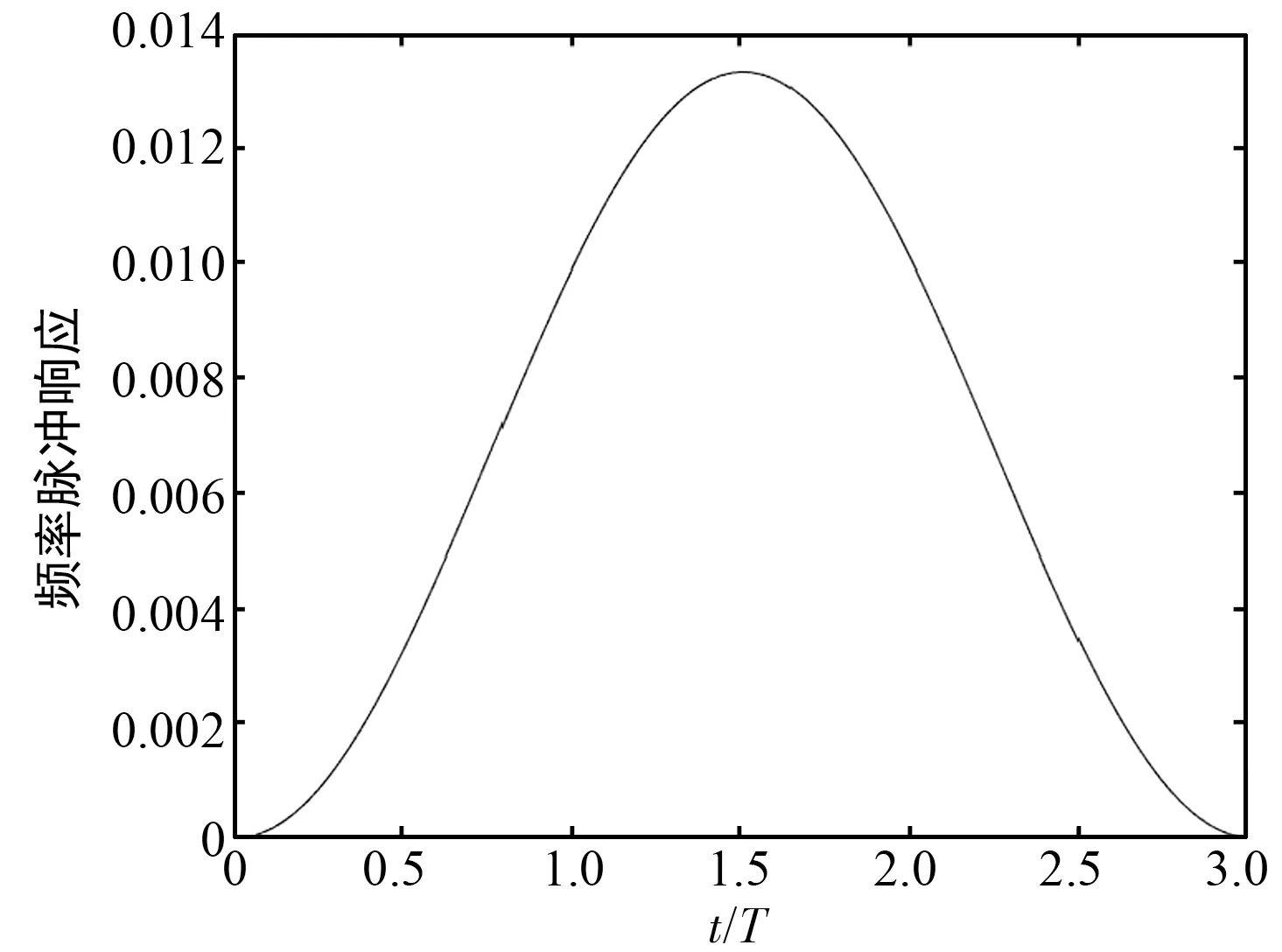
(a) 频率脉冲响应

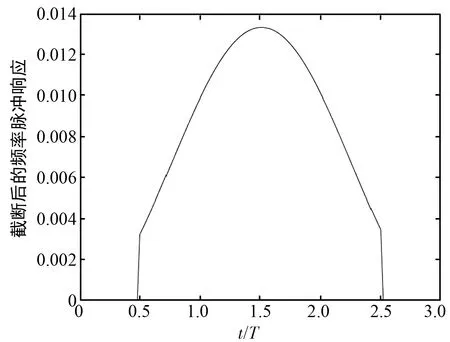
(b) 截断后的频率脉冲响应

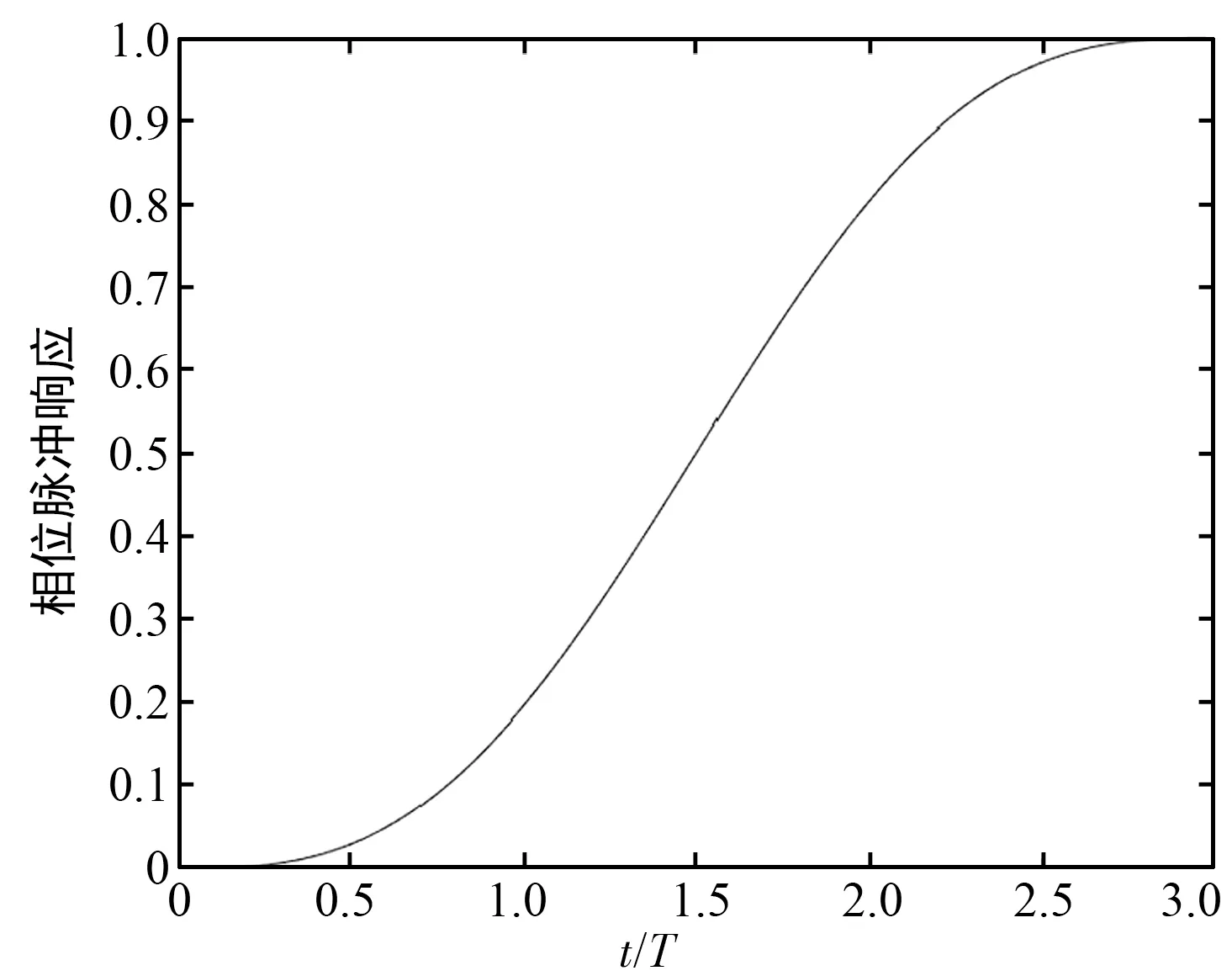
(c) 相位脉冲响应

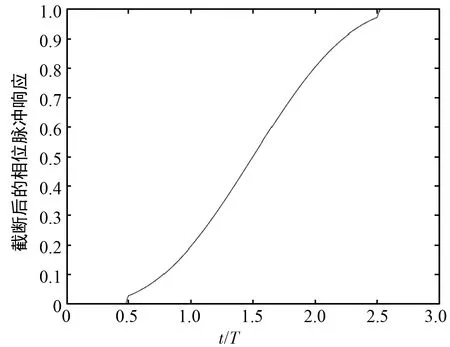
(d) 截断后的相位脉冲响应图3 频率脉冲响应截断算法示意图Fig.3 Frequency pulse truncation algorithm

检测区间发生变化后,Multi-h CPM的匹配滤波器构造如下:

(20)

使用了FPT算法之后,由于降低了响应长度L,Viterbi解调的网格状态数也降低为原来的1/M,从而有效降低了解调器的资源开销。但是不同于TP算法,FPT算法本质上是一个近似方法,会带来一定的串扰导致系统性能发生损失,不过其损失较小,对系统的影响可以忽略不计。

2.4 Multi-h CPM时频同步算法

2.4.1 定时同步算法

式(9)中,接收信号仅考虑噪声的影响,但在实际系统中,接收信号存在链路衰减、链路延迟和多普勒频偏等,因此实际的接收信号重新写作:

r(t)=Aej(2π(fc+Δf)(t-τ(t))+φ(t-τ(t);a))+n0(t),

(21)

式中:A是信号幅度,fc是中频频率,Δf是多普勒频移,τ(t)是链路延迟。因此接收机在进行Multi-h CPM信号解调时,需要保证接收机的本地信号和接收信号的时频同步。

假设仅存在定时偏差而不存在频率偏差时,Viterbi解调的累计度量值可以表示为:

(22)

图4给出了Multi-h CPM信号中定时误差对Viterbi解调的累计度量值的影响。可以看出,当接收机存在定时偏差时,Viterbi解调的累计度量值将会降低。利用该特点,可以采用超前-滞后门结构进行Multi-h CPM的定时同步。

超前支路信号rE和滞后支路信号rL可以表示为:

(23)

在[-0.5T,0.5T),超前支路累计度量值λE及滞后支路累计度量值λL相对于定时误差表现为凸函数,利用该特点可设计定时归一化度量值β来衡量超前支路累计度量值及滞后支路累计度量值的差值,其计算公式为:

(24)

当Multi-h CPM的调制参数确定后,定时归一化度量值β相对归一化定时误差Δt/T的曲线是固定的。从图5中可以看出,在[-0.5T,0.5T),定时归一化度量值β(Δt)与定时误差Δt近似成线性关系,在设计中作为定时误差估计曲线使用。基于上述曲线,在计算获取了超前支路累计度量值λE及滞后支路累计度量值λL后,通过计算定时归一化度量值,对照定时误差曲线,即可获得Multi-h CPM接收机的定时误差,修正定时误差即可完成定时同步。

2.4.2 频率同步算法

假设仅存在频率偏差而不存在定时偏差时,Viterbi解调的度量值可以表示为:

(25)

频率误差与累计度量值的关系图如图6所示,可以看出,当接收机存在频率误差时,累计度量值将会降低。与定时同步类似,可以采用升降频门结构进行频率同步。

图6 频率误差与累计度量值的关系图Fig.6 Effect of frequency error on metric values

升频支路的信号rU可以表示为:

(26)

降频支路的信号rD可以表示为:

(27)

对升频支路和降频支路的累计度量值进行归一化,可以得到频率归一化度量值:

(28)

当Multi-h CPM的数据速率为50 Mbit/s时,接收机的载波频率误差Δf对累计度量值的影响在[-80 kHz,80 kHz]呈现为凸函数,通过上述归一化设计后可以获取频率度量曲线,如图7所示。计算频率归一化度量值β(Δf),可以通过其曲线获取接收机的频率误差,修正频率误差即可完成频率同步。

图7 归一化频率误差曲线图Fig.7 Normalized frequency error curve

3 FPGA平台设计方案

3.1 整体设计方案

整个Multi-h CPM接收机整体结构如图8所示。接收机主要包括了信号预处理模块、SOVA解调模块、定时同步模块和频率同步模块。

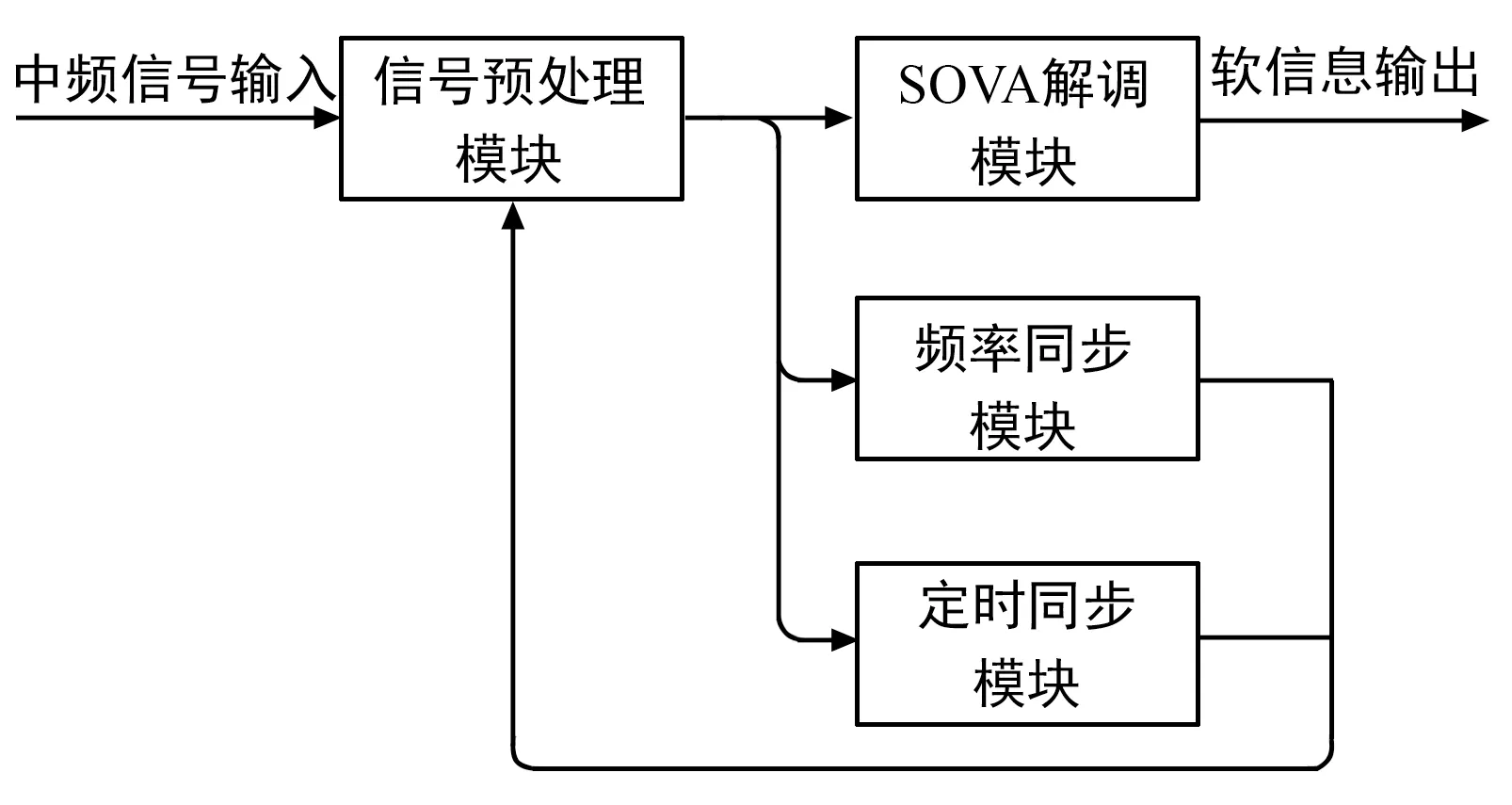
图8 Multi-h CPM接收机整体框图Fig.8 System block diagram of the Multi-h CPM receiver

信号预处理模块主要完成信号的预处理操作,包括对接收的中频信号进行去载波、为定时同步模块生成超前-滞后信号以及为频率同步模块生成升降频信号等操作。

SOVA解调模块主要完成Multi-h CPM的解调并生成软信息。整个SOVA过程中需要完成度量值计算、加比选以及路径回溯等操作。

定时同步主要修正接收机的定时误差,需要计算超前支路和滞后支路的累计度量值并且获取定时同步的误差值。

频率同步主要修正接收机的频率误差,需要计算升频支路和降频支路的累计度量值并且获取频率同步的误差值。

3.2 信号预处理模块

接收机从ADC处获取到高速中频数据流之后,首先对信号进行去载波操作,将信号从中频信号转为基带信号。降频处理由DDS载波生成器和FIR低通滤波器构成,其中DDS生成载波的具体数值由频率控制字决定,其计算公式为:

(29)

式中:fCLK为接收机主频,fIF为中频信号频率。为了保证DDS生成的信号频率精度,采用了32 bit的频率控制字,可以保证接收机生成的正弦信号频率误差小于0.1 Hz。

同样,升频支路和降频支路的信号也是通过DDS和FIR滤波器生成,通过更改频率控制字即可生成所需的不同频率信号。

对于超前支路和滞后支路的信号,通过对ADC的数据流进行延迟操作得到。未延迟的信号作为超前支路信号,延迟一次的信号作为正常的接收信号,而延迟两次的信号作为滞后支路信号。

3.3 SOVA解调模块

如图9所示,SOVA解调模块在接收到预处理模块的基带Multi-h CPM信号后进行信号解调,并且根据整个解调算法的处理步骤,可以细分为分支度量值计算单元、加比选单元、路径回溯单元和控制单元。

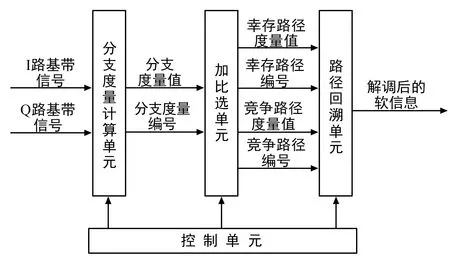
图9 SOVA解调示意图Fig.9 SOVA demodulator

控制单元为分支度量计算单元、加比选单元和路径回溯单元提供调制参数信息,并且对3个模块进行流程控制和协调,保证输入的基带信号可以以流水线形式完成数据处理。

分支度量计算单元接收前级预处理模块输入的I、Q两路基带信号与控制单元输入的调制参数信息。分支度量计算单元根据调制参数确定本地信号的生成,并且由内置的符号计时器计时确定当前的调制指数h。在得到相关的信息之后生成接收机本地信号,然后通过矩阵乘法完成分支度量的计算,将分支度量矩阵的结果输入到加比选单元。

加比选单元接收到分支度量计算单元不同状态下各个支路的分支度量值之后,通过控制单元输入调制指数信息,确定加比选的执行逻辑。加比选单元会在每个状态前一个符号周期存储的累计度量值的基础上,由当前的调制指数选择该状态所对应的分支度量值矩阵的分支,并将前一状态的累计度量值与对应的分支度量值相加,计算得到的新的分支度量值,并取度量值最大的路径作为幸存路径,次大的路径作为竞争路径,并将两个路径的信息输入到路径回溯单元。

路径回溯单元根据幸存路径的路径编号回溯度量值矩阵,并且根据回溯过程的各个状态确定解调的硬判决结果。此外,路径回溯单元利用幸存路径和竞争路径的累计度量值和比特硬判决结果,更新内部可靠性度量矩阵。完成路径回溯后,获取当前时刻累计度量值最大的状态和状态对应的可靠性度量,计算其对数似然比并作为最终软信息结果。

3.3.1 分支度量计算单元

分支度量计算单元的基本结构如图10所示。SOVA解调控制单元输入的调制参数信息,一方面,输入到修正参数计算器中,控制倾斜相位修正ROM地址,从本地存储的倾斜相位ROM中读取对应的倾斜值,与输入的I、Q两路信号进行复乘从而获取对应的经TP处理后的I、Q路信号。另一方面,调制参数输入到本地滤波器地址控制器中,经过地址控制器的计算后转换为本地滤波器地址,本地滤波器地址从本地滤波器ROM阵列中读取形成所有匹配滤波器对应的接收机本地信号。本地信号与经过TP处理的I、Q基带信号进行并行相关,即可得到SOVA解调的分支度量值。

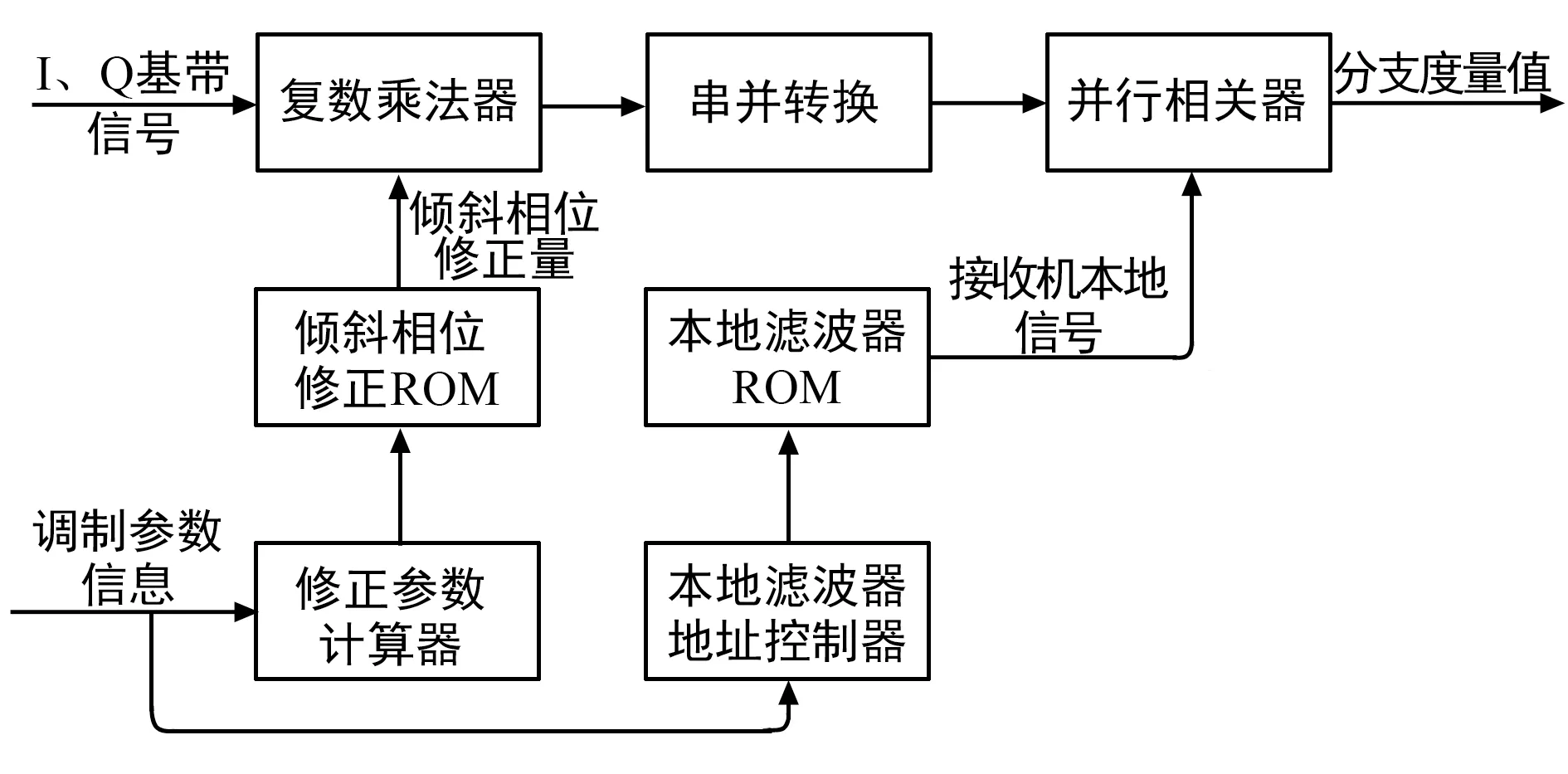
图10 分支度量计算单元示意图Fig.10 Branch metrics computing unit

并行相关器是分支度量计算单元的核心。以Multi-h CPM的调制参数M=4,L=3,h={5/16,6/16}为例,为了提高解调器的数据处理能力,在进行分支度量计算时需要对所有状态下的所有分支进行并行计算。即使采用了TP算法和FPT算法,Multi-h CPM依旧存在64个网格状态,256路分支路径,完全并行计算需要消耗大量的计算资源。为了简化并行相关器的计算复杂度,将整个相关运算拆解为接收信号复乘16组本地信号和对复乘结果进行两级相位旋转修正两个步骤完成。

考虑到对于单一复数a+bi,对其进行角度为π/2、π和3π/2的相位旋转后得到的结果分别为b-ai、-a-bi和-b+ai。在256路分支路径计算过程中,存在周期为4的相位旋转角度为π/2整数倍的情况,因此通过计算其中64路的分支路径结果,就可以得到所有的256路分支度量值。而在进行64路分支度量值的计算过程中,可以再一次利用相位旋转的思想进一步简化计算量。假设所有本地信号的初相为0,64路本地信号就可以进一步被简化成16路信号,计算得到16路相关值后,对相关结果乘以π/8、π/4和3π/8的信号相位,可获得剩余的48路相关结果。整个并行相关器的硬件实现架构如图11所示。

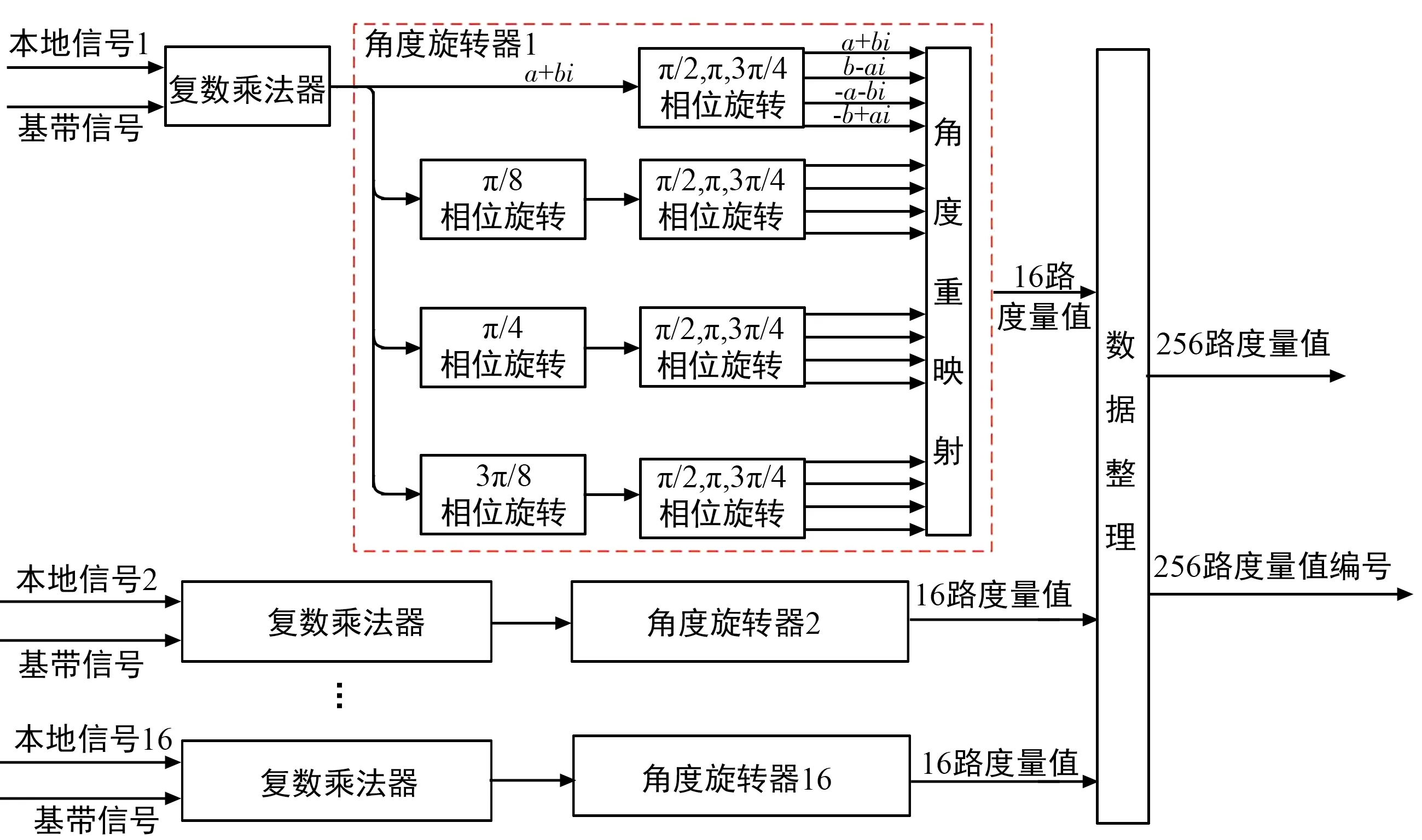
图11 并行相关器示意图Fig.11 Parallel correlator

不利用分支度量的相位旋转,需要同时并行256路复数乘法器。采用了相位旋转之后,只需要消耗16个复数乘法器和48个CODIC旋转器,就可以有效降低整体的资源消耗。同理,经过了分支度量单元之后,输入信号数率从采样速率降低到了符号速率,也降低了后级模块的数据处理压力。

3.3.2 加比选单元

加比选单元主要完成对各个状态下所有分支路径的度量值累加、比较和选择。来自控制模块的调制参数输入映射表中,确定来自分支度量计算单元生成的分支度量结果的具体映射方案。

整个加比选单元的硬件结构如图12所示。加比选单元中的状态分支度量映射实际是一个分选器,根据当前时刻每个状态的来源路径将所有的分支度量值映射至不同的状态中,即256路分支度量值每4个一组对应到Viterbi解调的64状态下。64个不同的状态都会从公用的累计度量值存储阵列中获取其对应的前一时刻累计度量值,随后利用其私有的加法器将分支度量值与前一时刻累计度量值相加得到4个累计度量值。4个累计度量值通过一个选择器,取其中最大的度量值作为当前时刻幸存路径的累计度量值,并将最大度量值所对应的路径记录为幸存路径,次大的累计度量值作为当前时刻竞争路径的累计度量值,其所对应的路径为竞争路径。

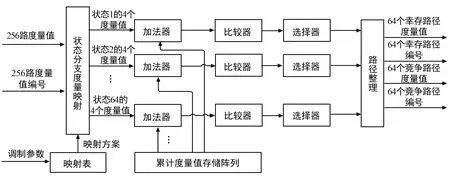
图12 加比选单元示意图Fig.12 Add-compare-select unit

在本单元的设计中,其所处理的数据速率远低于分支度量计算单元的数据速率,因此相比于分支度量计算单元需要全并行计算,加比选单元可以采用串并结合的方式完成计算,有效降低FPGA资源消耗。

3.3.3 路径回溯单元

路径回溯单元中存储有每个状态对应的可靠性度量矩阵。取SOVA的回溯长度为10,则每个状态均需要存储大小为10×4=40的可靠性度量矩阵。为了保证路径回溯的处理能力,10路路径回溯是并行处理。

整个路径回溯单位的硬件架构如图13所示。输入的路径度量值会首先会通过缓存比较器选出累计度量值最大和次大的状态。之后根据幸存路径和竞争路径的编号值,控制回溯地址从缓存阵列中获取前一时刻的度量值进行路径回溯,并且在回溯的同时要计算当前状态下的可靠性,将可靠性数据存储在可靠性度量矩阵之中。在计算可靠性数据的同时还需要对幸存路径和竞争路径下的解调比特结果进行判决,当幸存路径和竞争路径的硬判决比特结果不同时,对可靠性数值进行更新。

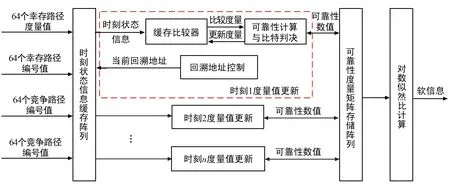
图13 路径回溯单元示意图Fig.13 Traceback unit

当回溯完成后,由于可靠性度量值矩阵中存储的是M进制符号的可靠性,还需要进行解映射操作,计算信息比特的对数似然比信息,才能得到最终的软信息结果。

3.4 时频同步模块

时频同步模块的具体结构如图14所示。整个时频同步过程包含了4个简化的前向Viterbi计算,信号预处理模块产生的超前-滞后信号和升降频信号,通过前文所述的分支度量计算单元和加比选单元,分别计算超前支路、滞后支路、升频支路和降频支路的累计度量值。计算获得累计度量值之后,不同于SOVA解调需要进行路径回溯,在升降频模块中仅需要计算各个支路的累计度量值的最大值。

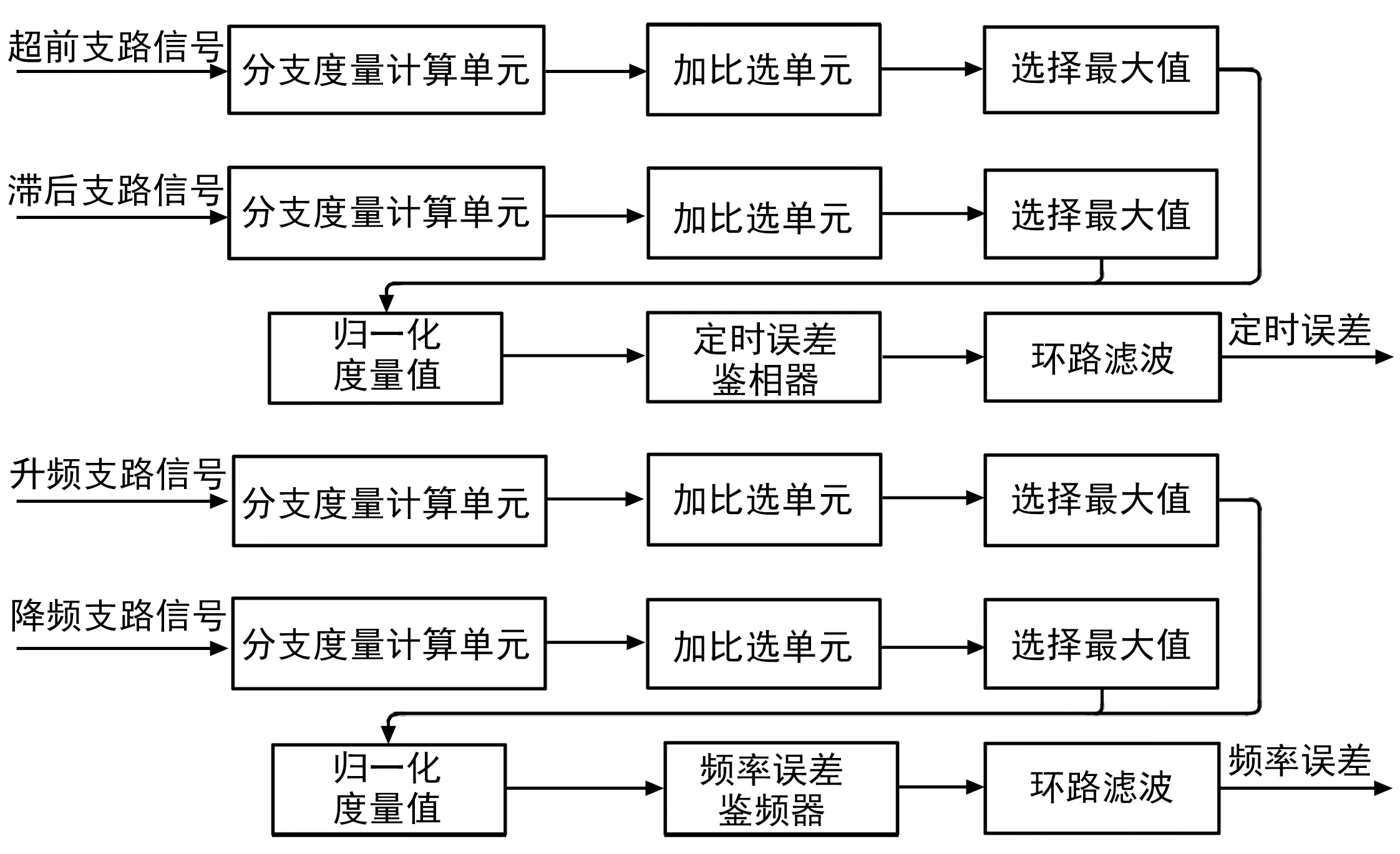
图14 时频同步模块示意图Fig.14 Time and frequency synchronizer

将超前支路和滞后支路的最大值送入到归一化模块中,计算得到定时归一化度量值,通过定时误差鉴相器得到接收机的定时误差。定时误差鉴相器本质上是一个查找表的ROM,其定时归一化度量值即为查找表的数据地址,根据不同的归一化度量值从ROM中获取定时误差。考虑到接收机数据存在噪声,直接计算得到的定时误差数值波动较大,因此通过一个环路滤波器,提高系统抗干扰能力。

频率同步与定时同步类似,根据升频支路和降频支路的累计度量最大值,获取频率误差结果。获取到定时误差和频率误差结果之后,将误差值反馈到信号预处理模块,修正定时误差和频率误差,完成接收机的时频同步。

4 实验

本文在FPGA硬件板卡对Multi-h CPM接收机的性能进行了测试。选取Multi-h CPM的信息速率为50 Mbit/s,调制进制M=4,关联长度L=3,采用的调制指数集h={5/16,6/16},并且在进行SOVA解调时,一次处理的数据块包含了20个数据符号。通过FPGA内部的集成逻辑分析仪(Integrated Logic Analyzer,ILA)抓取FPGA内部的数据运行结果,进行结果分析。

由图15可以看出,在初始的定时误差设置为0.25T的情况下,硬件系统可以在200个符号内完成定时同步的跟踪与锁定,且最终定时误差稳定在0附近,证明定时误差得到了修正。同时可观察到,在定时跟踪前期由于起始相位越界,同步过程中出现了波动,但后续状态稳定后没有发生类似的情况,证明FPGA环路能够实现稳定的定时跟踪。

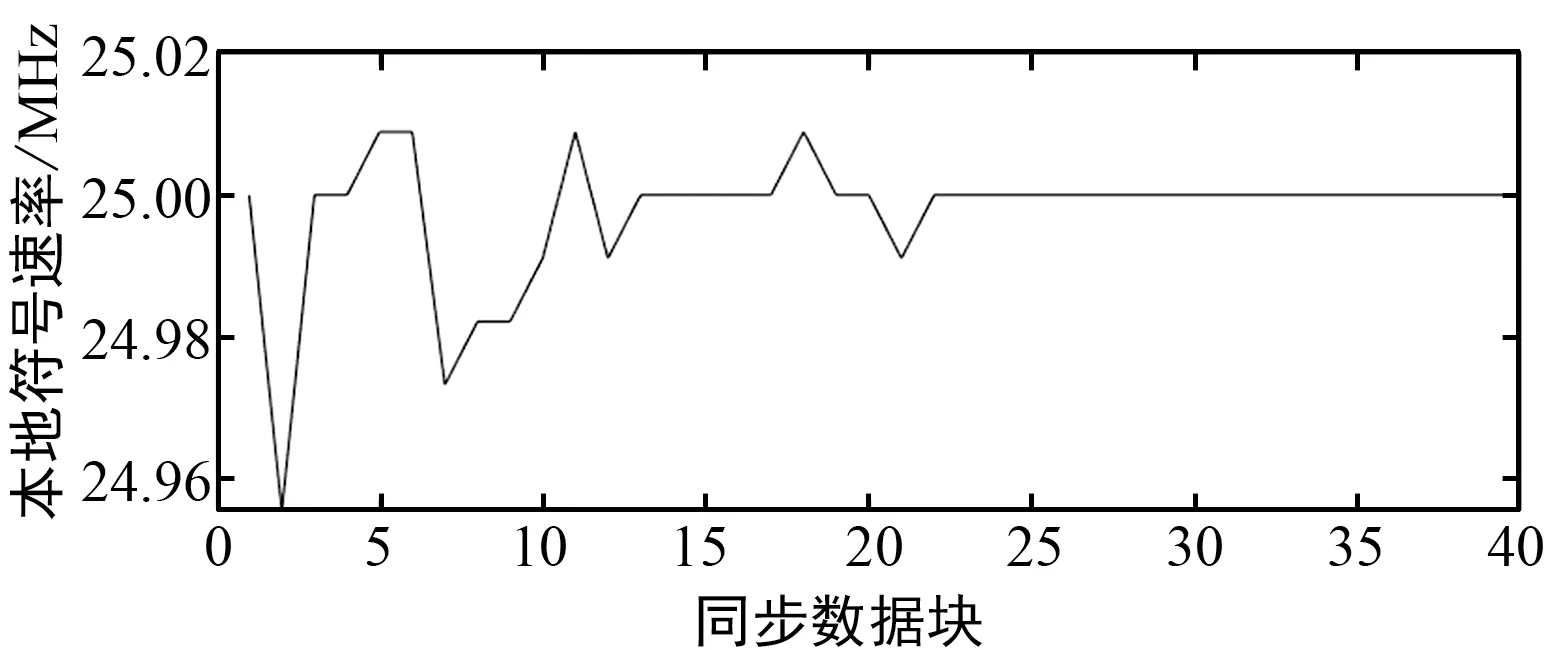
(a) 符号速率同步过程

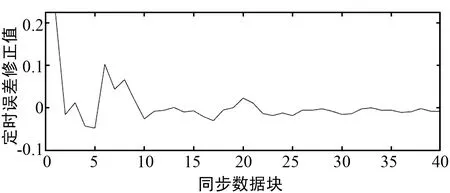
(b) 定时误差修正值图15 定时同步结果图Fig.15 Timing synchronization results

由图16可以看出,在初始的频率误差设置为150 kHz的情况下,硬件系统可以在200个符号内完成频率同步的跟踪与锁定,且最终频率误差稳定在0附近,证明频率定时误差得到了修正。同时可知,在频率跟踪过程中存在过冲,但过冲的幅度不大,信号载波频率波动较小,并且环路稳定后没有发生类似的情况,证明FPGA环路能够实现稳定的频率跟踪。

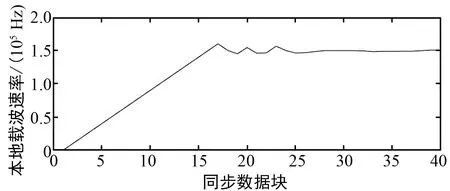
(a) 本地载波频率同步过程

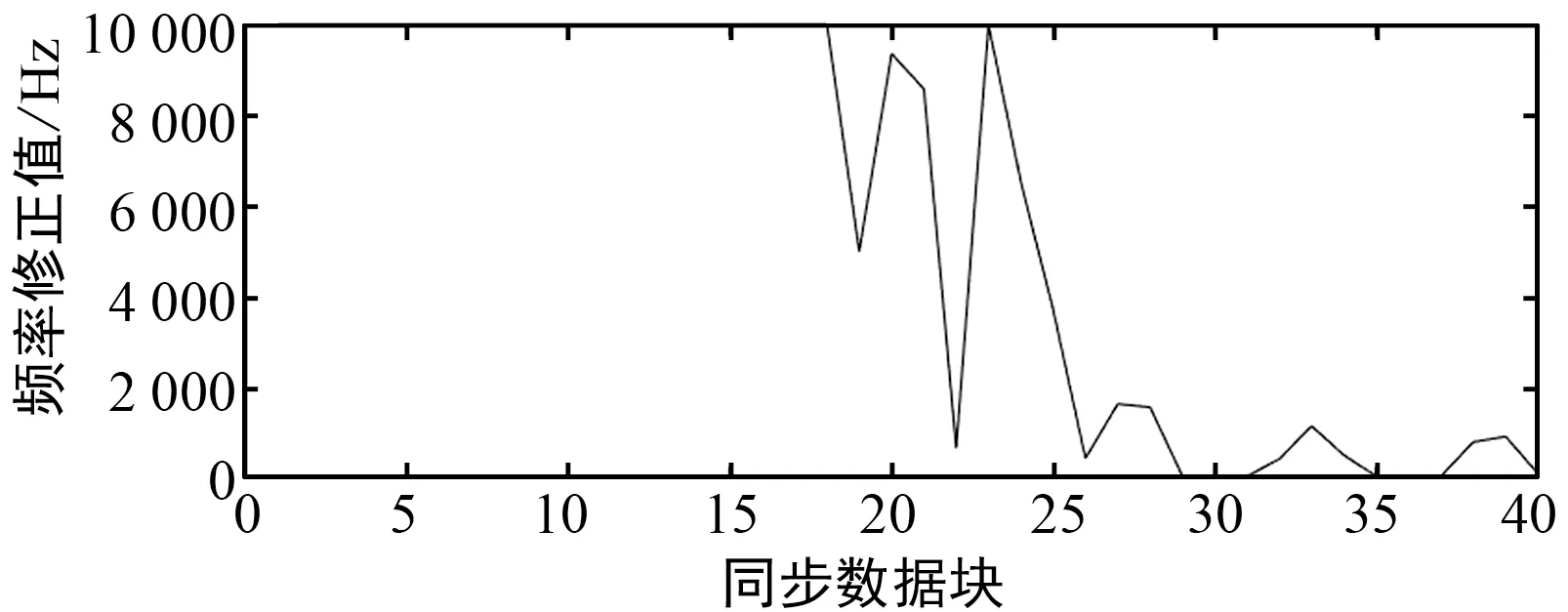
(b) 频率误差修正值图16 频率同步结果图Fig.16 Frequency synchronization results

在测试环境中追加150 kHz的多普勒频移和50 kHz/s的动态多普勒变化率,测试整个接收机系统在高动态多普勒环境下的解调能力。从图17的BER曲线可以确认定时和频率同步环路可以正常工作,没有发生定时或者频率同步环路失锁的情况,即使在低信噪比情况下,定时同步和频率同步依旧可以稳定跟踪时频误差。

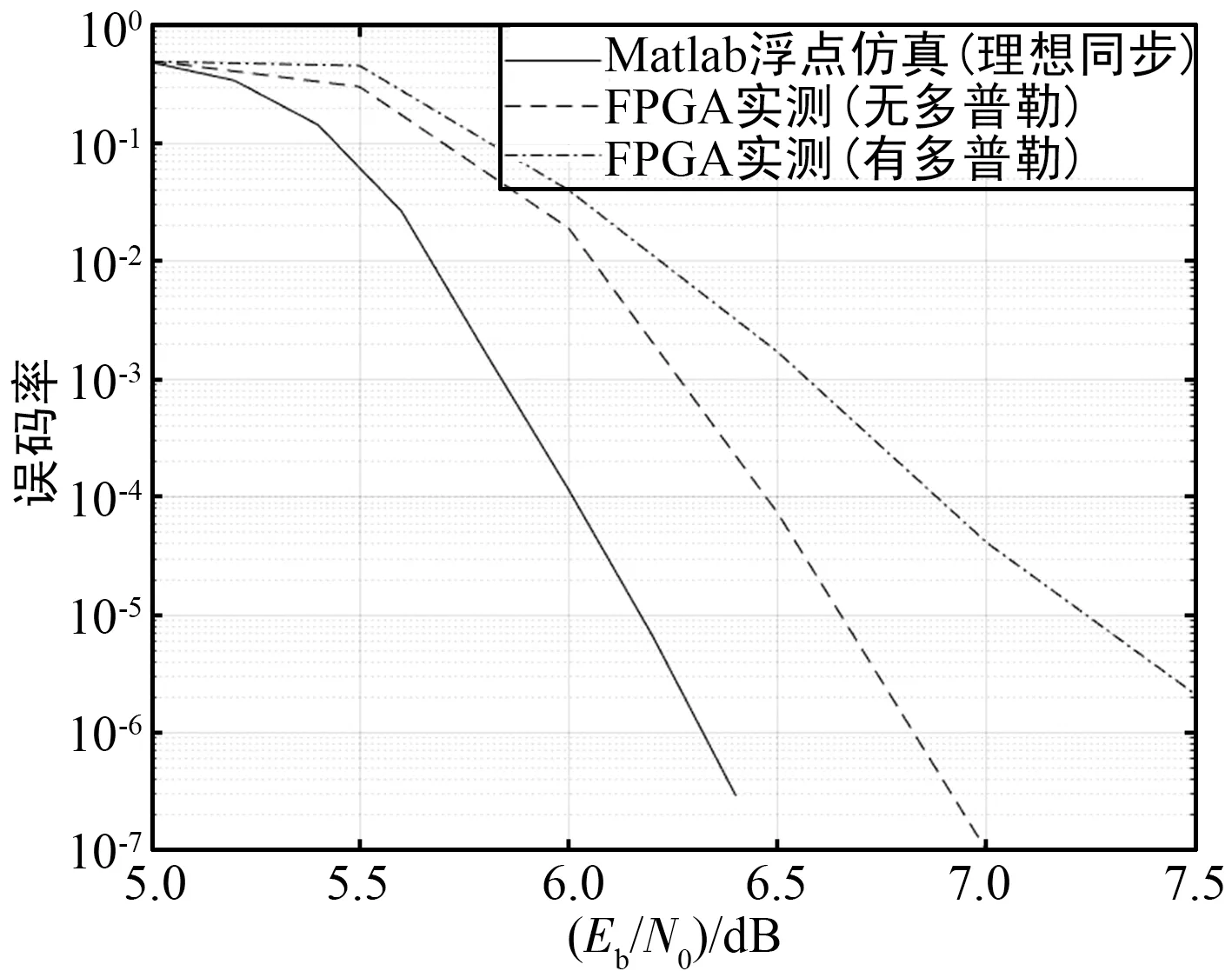
图17 误码率曲线Fig.17 BER curve

由图17可以看出,相比在Matlab软件中理想同步情况下的浮点仿真,基于FPGA平台搭建Multi-h CPM解调系统后,误码率性能存在一定的劣化。在无多普勒情况下,BER=10-5时的劣化程度约达0.45 dB。该劣化一方面来源于FPGA内部的定点量化损失,另一方面来源于定时同步损失。在高动态多普勒情况下,取BER=10-5为基准进行观察,接收机的实测性能损失从无多普勒频偏情况下的约0.45 dB提升至了1.2 dB,但该性能损失在实际系统中可以接受。

5 结束语

本文分析了Multi-h CPM调制解调原理和时频同步方案,设计了基于FPGA平台的Multi-h CPM接收机架构。针对Multi-h CPM接收机复杂度较高的问题,通过采用TP算法和FPT算法简化了Viterbi网格状态数,并且在FPGA中利用角度重映射思路,通过使用CODIC IP核代替了大量的复数乘法器,降低了系统的资源开销,保证了解调系统可以在FPGA实现高并行处理,提高了系统吞吐率。

本文通过ILA验证了程序在FPGA内部执行的稳定性和可靠性,结果表明本文设计的接收机架构在高动态多普勒环境下可以稳定实现时频同步功能,并且接收机的性能损失较小,具有良好的应用前景。