海潮模型在北斗精密单点定位中的影响分析
冯建强,边 超,王 乾
(1.南水北调中线信息科技有限公司,北京 100038;2.山东黄金集团蓬莱矿业有限公司,山东 烟台 265621)
海潮负荷是指海水质量周期性地作用于地球表面,使地球表面发生弹性变化[1]。研究表明,海潮负荷会对全球卫星导航系统(GNSS)的导航与定位产生厘米级影响,且沿海地区的影响是内陆地区的4~5倍[2]。精密单点定位(PPP)技术具备无需基准站、不受距离限制、高精度和低成本的优点,受到GNSS 用户青睐和支持[3-5]。王俊杰[6]等依托福建GNSS对闽海潮负荷位移进行了研究,结果表明海潮模型差异主要影响海潮负荷垂直分量,其影响数值是水平分量的3 倍左右;魏国光[7]等对香港地区GNSS 观测数据进行静态PPP 解算,获取PPP 坐标时间序列,求取分潮负荷位移参数,结果表明不同测站PPP 反演结果存在差异性,反演负荷位移参数在垂直分量上优于全球海潮模型;赵红[8]等利用改进的动态PPP 技术建立了香港地区海潮负荷位移模型,其精度优于静态PPP构建的海潮负荷位移模型,有效提高了海潮模型的适应性。2020年北斗卫星导航系统(BDS)正式组网完成,在导航、定位和授时方面均取得快速发展和应用[9-10]。目前针对海潮模型在BDS PPP中的研究还较少,本文基于国际GNSS服务组织(IGS)分析中心提供的观测数据,对比分析了海潮模型在BDS-2、BDS-3 和BDS-2+BDS-3 PPP中的影响。
1 海潮负荷的数学模型
海潮负荷的数学模型采用负荷格林函数褶积积分法表达,由海潮瞬时潮高和格林函数褶积积分求取,即[11]
式中,Lu、Lw、Ls分别为海潮负荷引起的站点径向、西向和南向位移;ρω为海水密度;φ、λ为计算点球坐标;φ′、λ′为负荷点球坐标;t为计算天文幅角初相开始时间;ψ为计算点到负荷点的球面角距;A为计算点到负荷点的球面方位角;为瞬时潮高;U(ψ)和V(ψ)分别为垂直和水平方向上的格林函数。
式中,k、g 分别为引力常数和重力常数;R 为地球半径;、为n阶负荷勒夫数;Pn()cosψ为勒夫让德函数。
测站与负荷点的球坐标有以下关系[12]:
瞬时潮高一般可展开为若干调和分潮潮高的总和,计算公式为:
式中,N为叠加潮波数;ωk为各分潮角频率;xk为各分潮天文幅角;ξk、δk分别为各分潮坐标分量的振幅和相位。
一般在计算过程中,海潮负荷只考虑4 个半日分潮、4个全日分潮、半月波、月波和半年波11个主要分潮的影响。
2 数据来源与方案设计
2.1 数据来源
为对比分析海潮模型在BDS-2、BDS-3 和BDS-2+BDS-3 PPP中的定性、定量影响,本文选取亚太地区具有BDS 观测数据的IGS 观测数据,借助Bernese 软件进行PPP 处理,卫星星历均采用事后精密星历。按照测站所在位置与海洋距离的远近,将测站划分为沿海、内陆两种,11个测站属于沿海地区、19个测站属于内陆地区。
2.2 方案设计与处理策略
本文设计了6 组对照实验,参数配置遵循控制变量法,其中方案1和方案2(BDS-2)、方案3和方案4(BDS-3)、方案5 和方案6(BDS-2+BDS-3)分别为对照实验。方案1~6 静态PPP 解算的卫星截止高度角均设置为10°,对流层延迟采用Saastamoinen 模型+GMF映射函数进行削弱改正,电离层延迟采用双频观测值消除电离层延迟影响,卫星星历采用IGS 数据中心公布的事后精密星历,天线相位采用IGS14 模型进行改正,固体潮采用IERS模型进行改正;方案2、方案4 和方案6 海潮模型采用FES2004 模型进行改正,方案1、方案3和方案5不进行改正。
3 结果分析
本文按照PPP 处理参数配置表进行PPP 解算,将2020 年年积日200~260 每天PPP 结果分别与以IGS 数据中心提供的测站三维坐标进行对比分析,并将两种模式解算结果与IGS 测站差值的互差作为海潮负荷位移量;同时进一步统计三维坐标互差的均方根(RMS),用以评价外符合精度。
3.1 海潮模型对BDS-2 PPP的影响分析
根据方案1 和方案2,统计两种模式解算2020 年积日200~260的测站结果与IGS测站差值的互差(表1)和RMS值(图1),可以看出,海潮模型对BDS-2 PPP在U 方向产生的位移大于N、E 方向的位移量,其中ABMF 站在U 方向的位移为厘米级,其原因可能是ABMF 站位于海洋地区,受海潮影响较大;海潮负荷模型对BDS-2 PPP 在N、E 和U 方向产生的位移均值为2.60 mm、3.02 mm、5.51 mm;各测站BDS-2 PPP均在U 方向误差最大,5 个测站在海潮模型改正前后定位结果均优于1 mm,其原因是接收卫星个数较多、数据观测质量较好、定位精度较高;加入海潮模型后,各测站在N、E 和U 方向定位误差均有所改善,但改善量有所区别,可能是由不同站点所处位置不同引起的。沿海和内陆地区测站海潮负荷模型均对PPP结果产生一定影响,总体而言,海潮模型使BDS-2 PPP 结果在N、E 和U 方向精度分别提升20.18%、20.20%、25.40%,U方向精度提升最显著,这与参考文献[13]的研究结果相吻合。

图1 BDS-2 PPP三维坐标残差RMS值

表1 海潮模型对BDS-2 PPP的位移量/mm
3.2 海潮模型对BDS-3 PPP的影响分析
根据方案3 和方案4,统计两种模式解算2020 年积日200~260的测站结果与IGS测站差值的互差(表2)和RMS值(图2),可以看出,海潮模型对BDS-3 PPP在N、E 和U 方向产生的位移量均为毫米级,在N、E和U方向产生最大位移量分别为4.87 mm、4.95 mm 和8.88 mm,均值分别为2.85 mm、3.92 mm 和5.31 mm;各测站BDS-3 PPP 均在U 方向误差最大,在N、E 和U 方向最佳定位RMS 值分别为1.10 mm、1.50 mm、6.02 mm,海潮模型改正后,在N、E和U方向最佳定位RMS 值分别为0.83 mm、1.27 mm、5.15 mm;总体而言,海潮模型使BDS-3 PPP 结果在N、E 和U 方向精度分别提升14.81%、14.22%、15.30%,这与参考文献[14]的研究结果一致。

图2 BDS-3 PPP三维坐标残差RMS值
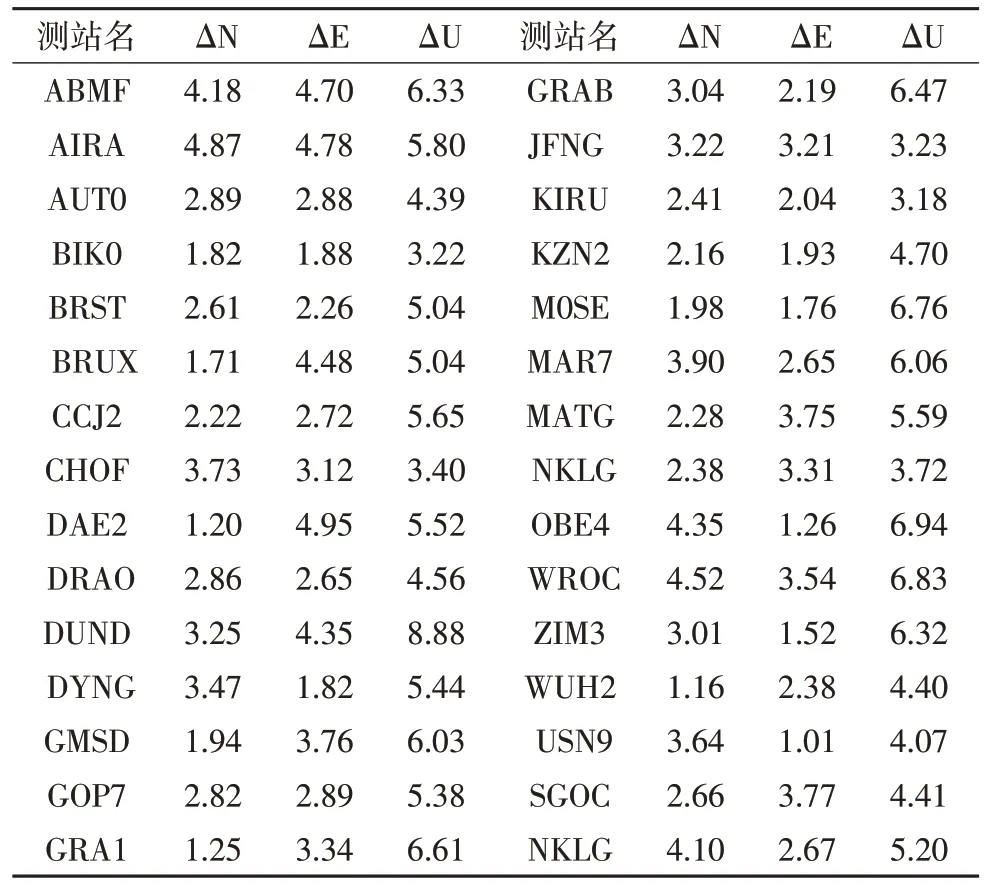
表2 海潮模型对BDS-3 PPP的位移量/mm
3.3 海潮模型对BDS-2+BDS-3 PPP的影响分析
根据方案5和方案6,统计两种模式解算2020年积日200~260 的测站结果与IGS 测站差值的互差(表3)和RMS 值(图3),可以看出,海潮模型对BDS-2+BDS-3 PPP 在N、E 和U 方向产生的位移量均为毫米级,在N、E和U方向产生最大位移量分别为3.49 mm、3.67 mm和5.91 mm,均值分别为2.27 mm、2.22 mm和4.10 mm;与BDS-2、BDS-3 PPP 相 比,BDS-2+BDS-3 PPP 结果精度明显提高,海潮模型改正前BDS-2+BDS-3 PPP 在N、E 和U 方向的最佳定位RMS值分别为0.81 mm、0.52 mm、3.63 mm,改正后的最佳定位RMS 值分别为0.74 mm、0.46 mm、3.10 mm;总体而言,海潮模型使BDS-2+BDS-3 PPP 结果在N、E和U方向精度分别提升9.13%、9.41%、10.01%,这与参考文献[13]的研究结果吻合。与BDS-2、BDS-3 PPP相比,海潮模型对BDS-2+BDS-3 PPP精度提升量较小,且在三维方向提升精度相当,其原因可能是BDS-2+BDS-3 PPP精度较高导致误差改善量受限。

图3 BDS-2+BDS-3 PPP三维坐标残差RMS值

表3 海潮模型对BDS-2+BDS-3 PPP的位移量/mm
4 结语
本文分析了海潮模型对BDS-2、BDS-3 和BDS-2+BDS-3 PPP的影响,结果表明静态PPP过程中加入海潮模型,对BDS-2、BDS-3 和BDS-2+BDS-3 PPP 三维方向坐标精度均有不同程度的提升,提升效果均为毫米级,其中U 方向提升效果最佳,N、E 方向效果相当。与BDS-3 和BDS-2+BDS-3 PPP 相比,BDS-2 PPP 的提升效果更显著,可能是由BDS-3 和BDS-2+BDS-3 PPP 精度较高所导致的。因此,今后BDS PPP 过程中推荐加入海潮模型,以进一步提高PPP 精度。本文在实验过程中只对比分析了全球海潮模型(FES2004)对BDS PPP 的影响,不同海潮模型在不同地区的适应性将是后续研究的重点。

