基于规则网格的复杂断层网络处理与建模

牛露佳,王双威,曾义文,朱晨媛,王占刚

中国矿业大学(北京)地球科学与测绘工程学院,北京,100083

内容提要:断层建模是三维地质结构建模中的主要过程之一。断层面建模过程中需要根据断层间的空间接触或者切割关系进行几何曲面的裁剪,目前方法利用三角网求交算法进行曲面裁剪,但是该算法处理复杂断层面切割关系时往往不稳定。笔者等提出了基于规则网格的复杂断层网络处理与自动化建模的方法和流程,详细讨论了基于网格化的断层网络模型形式化理论表达、建模流程中的断层网络空间关系构建以及相交裁剪处理算法等核心步骤。利用测试数据和煤矿三维地震构造解释数据进行了验证,表明该方法可以有效处理多条互相切割、主辅关系复杂的断层网络,具有较好的算法稳定性;与SKUA—GOCAD断层建模方法对比,能够减少交互过程,提高断层建模的自动化程度。

三维地质结构建模(Structural Geological Modeling)用于构建结构模型来表达地下地质对象的几何形态及对象间的空间关系(Myers, 2003;Caumon et al., 2009;Wang Zhangang et al., 2016;Bi Zhengfa et al., 2022)。结构建模需要处理地质构造的接触关系以及切割关系,其中,断层建模主要解决断层面的构建以及切割关系处理问题。复杂断层网络处理切割关系主要涉及X型,Y型、λ型、T型、交叉型、半Y型和半λ型等断层间的组合方式(朱良峰等,2008;李兆亮等,2015)。

断层建模的一般流程是利用断层控制点或者断层棱边数据进行空间插值生成断层面,然后根据不同断层间的空间接触或者切割关系进行几何曲面的裁剪。断层面采用不规则三角网(TIN,Triangulated Irregular Network)表达,利用三角形求交进行曲面裁剪。这些算法需要显式处理断层网络中主辅断层的削截关系来提高断层建模的自动化程度,如基于测地线的路径切割算法(李兆亮,2015),断层的错动和错层处理(刘光伟等,2018)。在隐式地质建模(Renaudeau et al., 2019;Irakarama et al., 2021;de Kemp, 2021;Grose et al., 2021)中,断层的处理不依赖于三角网的求交,比如GemPy(de la Varga et al., 2019)以及Grose等(2021)根据断层两盘的运动学特征处理断层,这类方法需要断层的几何形态和运动学的数学描述,相关文献中呈现的断层以及切割关系相对简单。从以上研究可以看出,基于不规则三角网的断层面求交裁剪是复杂断层网络间切割处理与建模的主要手段。不规则三角网求交一般采用计算几何中的三角形求交算法以及改进算法(Moller, 1997;赵景昌等,2014),但是在实际应用中三角网求交算法稳定性差,直接影响着断层建模的自动化处理能力,尤其针对多期构造或者断层网络的处理(蒋钱平等,2008;Pellerin et al., 2014)。

不采用三角网求交算法进行复杂断层面切割裁剪处理是断层建模仍需研究和解决的问题。为此,表达三维地质结构的网格化模型与建模方法被提出以解决地质对象切割、剖切分析等方面的技术难点,比如GTP(吴立新等,2003),规则网格(Graciano et al., 2018),Cut-Cell网格(Mallison et al., 2014 ),角点网格(于瑞涛,2018)和广义棱柱网格(GPG)(Li Xin et al., 2018 )。基于网格化模型的切割算法可以有效实现地质体的剖切处理并取得了较好的效果,如李长春等(2008)基于GTP实现三维地质体的剖切,Zhou Cuiying等(2020)提出垂直投影三角形网格(VPTN)实现地质体的剖切。这类方法的特点是根据地质分层特性,地质界面的分片构成单元(四边形或者三角形)在空间XY方向上具有相同的离散结构,曲面分片单元顶点都在三棱柱或者四棱柱边上,分片单元的切割裁剪只需要在Z方向上进行求交处理,消除了几何图形求交算法的误差影响,保证了算法的稳定性(Zhou Cuiying et al., 2020)。研究人员也在探索利用网格化方法进行断层建模,比如基于GTP的断层交互建模(车德福等,2008),基于角点网格的局部多级加密(于瑞涛,2018)和六面体元角点移位(刘少华等,2022)。然而,这些方法以交互为主,能自动处理的断层比较简单。因此,自动化处理复杂断层网络的切割裁剪以及断层建模仍是一个问题。

由于网格化模型在切割算法稳定性方面的优势,笔者等提出基于网格化的断层网络模型形式化理论表达,基于此提出基于规则网格的断层网络建模流程,详细讨论了建模流程中断层空间关系构建以及断层相交裁剪处理方法。

1 方法原理

1.1 形式化理论表达

基于网格化的断层网络模型形式化表达为FaultModel={Ω,F,R},其中,定义域Ω={Ωj}表示模型整体空间XY方向的网格化离散域,Ωj是离散单元,类型可以是三角形、四边形等,j=1...m,m是离散单元数量;断层集合F={Fi},i=1...l,l表示断层的数量;断层空间关系集合R={rij},rij=表示两个不同断层Fi和Fj的空间关系。断层面Fi和关系rij的定义如下:

(1)断层面Fi是单值曲面,Fi的分段函数表达为:

u=(x,y),Fi的定义域Ω1∪Ω2∪…∪Ωn⊆Ω。显函数zi(x,y)为离散单元上的插值函数,描述断层Fi在(x,y)位置处的z值。

(2)断层空间关系rij定义两个断层面是否相交的拓扑关系以及两个断层面Z方向上的方向关系。

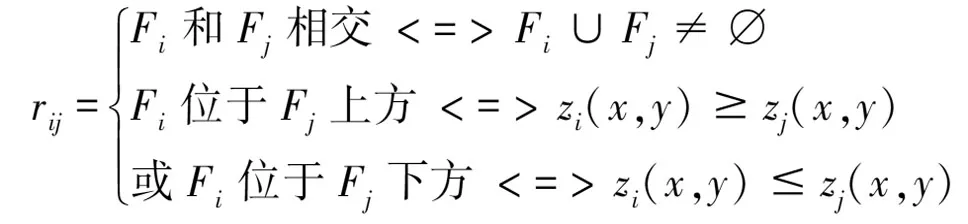
可见,由于关系rij定义了空间上下关系,不能处理X型断层组合。根据此关系可以得到如下推论:

推论1:Fi位于Fj的上方且Fj位于Fk的上方,则Fi位于Fk的上方。即:

zi(x,y)≥zj(x,y)且zj(x,y)≥zk(x,y),则zi(x,y)≥zk(x,y)

推论2:Fi位于Fj的下方且Fj位于Fk的下方,则Fi位于Fk的下方。即:

zi(x,y)≤zj(x,y)且zj(x,y)≤zk(x,y),则zi(x,y)≤zk(x,y)

Fi与Fj的关系rij根据实际地质情况,利用Fi与Fj的削截主辅关系以及形成先后顺序进行设置。

若Fj是主断层,Fi是辅断层,则Fj切割Fi,Fi和Fj相交且Fi位于Fj上方或Fi位于Fj下方。

如果离散单元采用三角形单元对定义域Ω进行网格化离散,地质模型表达和建模类似主TIN法(李元亨等,2010)或者GTP建模(吴立新等,2003;车德福等,2008)。

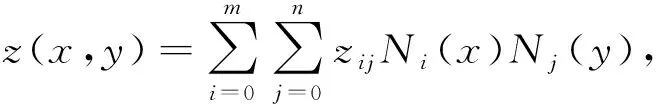
1.2 基于规则网格的断层面数据结构

将定义域Ω在XY方向上按一定分辨率均匀离散形成的规则网格称为基网格,基网格单元称为单元柱。如图1,断层面在基网格控制下进行网格化,在单元柱内中形成四边形对象称为Interface。断层面F由Interface拼合而成,即F={Interfaceij}={},Interface由5个属性组成,包括4个网格点z值和Interface所在断层F编码id。

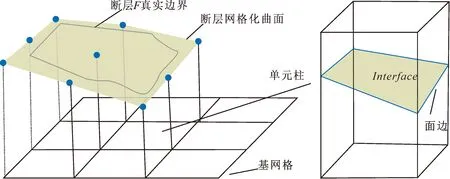
图1 断层F网格化 (a)和单元柱(b)Fig.1 Fault F in regular grid(a) and Pillar(b)

通过基于网格化的断层网络模型形式化表达和Interface定义,断层建模实质上将断层面按网格化生成后进行切割处理,核心过程是在基网格的单元柱内根据断层空间关系进行Interface的求交和裁剪处理。由于单元柱内不同Interface的差异是z值,求交和裁剪主要根据z值大小关系进行算法设计,有利于算法稳定性。断层空间上下关系决定了Interface间的上下关系,通过空间关系二叉树(见3.1)管理所有断层关系,达到自动化处理的目的。

2 总体实现流程

复杂断层网络建模处理流程如图2所示,主要步骤包括:

(1)基网格设置,根据建模源数据区域范围和建模网格分辨率将定义域在XY方向上均匀离散形成的基网格。

(2)断层网络空间关系构建,根据实际地质情况,利用断层的削截主辅关系构建断层空间关系,包括空间上下关系和相交关系。通过空间关系二叉树序列(见3.1节)记录所有断层空间上下关系,相交关系表记录断层相交关系。

(3)网格化断层面生成,逐个断层处理,根据当前断层F的区域范围,利用薄板样条插值算法或者有限差分插值算法(Irakarama et al., 2021)生成Interface拼合的网格化断层面,即F={Interfaceij}。同时,使用主成分分析法计算断层输入控制点的最佳投影面,在最佳投影面上提取断层边界的真实最小凸包并进行调整作为断层真实边界条件。

(4)断层边界延伸预处理,对空间关系二叉树中存在相交关系的断层将切割主断层面的区域范围外延至所有被切割辅断层区域范围的最小公共外包,并对延伸部分进行标记(见3.2节)。

(5)在单元柱内实现Interface相交裁剪,在单元柱内实现两个或者多个Interface四边形求交裁剪算法(见3.3节)。将隶属同一断层的Interface处理后的有效曲面拼接起来,进行Delaunay三角剖分生成相交裁剪后的三角网化断层面。

(6)后处理,利用断层真实边界条件对相交裁剪后的三角网化断层面进行边界裁剪,生成最终的断层面。后处理会消除断层网格化造成的 “假相交”切割关系(见3.1节)和断层延伸标记边界(见3.2节),保证断层网络模型空间拓扑的合理性。

下文将重点对断层间空间关系构建、断层边界延伸预处理和Interface相交裁剪3个核心步骤进行详细介绍。

3 核心步骤

3.1 断层网络空间关系

根据断层间空间关系rij的定义,使用空间关系二叉树和相交关系表记录断层空间位置上下和是否相交的信息。空间关系二叉树的数据结构定义如下:

FaultRelationBinaryTree {

树结点集合D:每个结点一一关联断层集合F={Fi}中对应断层;

结点关系集合H:结点关系为二元关系:

(1)D中存在唯一的根结点root,在关系H中无前驱;除根结点,其他结点必有唯一前驱结点,即父结点。

(2)除叶结点,每个结点至多有两个孩子结点,即左子结点和右子结点。

根据断层空间关系集合R={rij}构建结点关系,规定:父结点断层与左子结点断层和右子结点断层都相交;左子结点断层位于父结点断层上方;右子结点断层位于父结点断层下方。从断层主辅关系,相对于子结点,父结点为主断层结点。

空间关系二叉树描述了有切割联系的断层关系,当断层数量过多需要降低树深度,空间关系二叉树应满足平衡二叉树的结构要求(图3)。在整个建模工区,相互有切割联系的断层关系会形成多个空间关系二叉树,整体构成空间关系森林。空间关系二叉树按中序序列进行存储,每个断层记录按中序遍历的序列位置编号,形成断层关系存储表(图3c)。根据存储序列编号,无需遍历二叉树,通过编号顺序可判断出两个断层的空间上下关系,如判断断层F2与F4的空间上下关系,F2的中序遍历位置索引号(5)大于F4的索引号(1),故F2位于F4的下方。

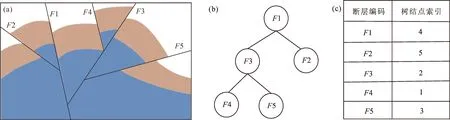
图3 断层模型剖面图(a)、空间关系二叉树(b)和存储表(c)Fig.3 Fault model section(a)、 Space relationship binary tree(b) and Storage table(c)

相交关系表记录任意两个断层间是否存在切割关系。相交关系表的意义在于处理断层网格化后的“假相交”关系,保证断层建模的正确性。断层“假相交”切割由规则网格分辨率引起。如图4(a)中断层F3切割F2,F2切割F1,而F1和F3实际中并没有相交。但是按断层网格化处理,由于网格分辨率,F3网格化后与F1相交(图4b)。“假相交”切割关系需要在相交关系表中设置F1和F3不相交,Interface相交裁剪步骤不处理F1和F3的切割关系,后处理步骤根据断层真实边界进行裁剪。

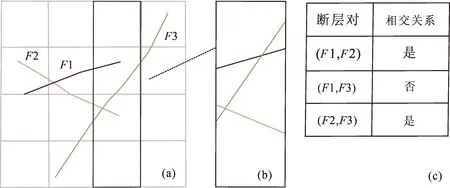
图4 断层切割示意图:(a) 断层实际分布、(b) 图框网格内断层网格化后结果和相交关系表(c)Fig.4 Faults cutting: (a) actual faults distribution, (b) faults in regular grid and intersecting relationship table (c)

3.2 断层边界延伸预处理

由于断层面裁剪在单个单元柱内进行处理,而裁剪前的断层所覆盖的单元柱会超出断层实际区域。如图5a所示,断层F1与F2相交,断层所覆盖单元柱有重叠域,也有非重叠域。若F1切割F2且F2在F1下方,在非重叠域上F2在裁剪处理后会出现错误(图5b),其原因在于F1为主断层切割辅断层F2,但是F2的单元柱超出了F1的覆盖范围。若将断层F1延伸到F1和F2边界的最小公共外包(图5c),可以保证断层裁剪的正确处理,得到如图5d所示结果。因此,断层边界延伸预处理就是对存在相交关系的主辅断层,将切割主断层的区域范围外延至所有被切割辅断层区域范围的最小公共外包,对主断层延伸部分进行标记。断层面后处理阶段应舍弃标记部分。

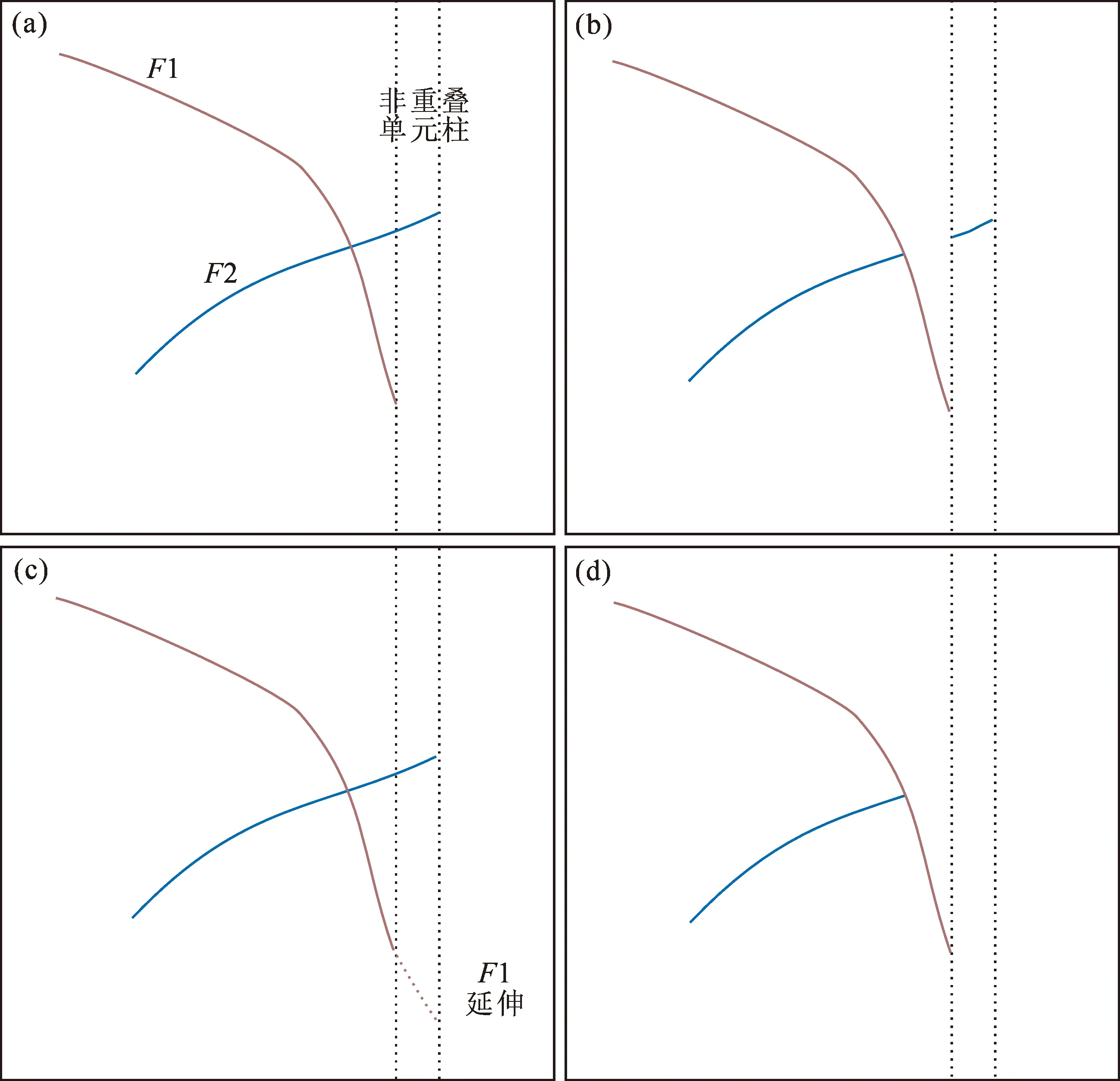
图5 断层延伸处理:(a)待处理断层;(b)不合理情况;(c)延伸处理;(d)最终结果Fig.5 Fault extension preprocess:(a) original faults; (b) unreasonable case; (c) fault extension; (d) final result

3.3 断层相交裁剪处理

断层相交裁剪只需在单元柱内实现Interface相交裁剪。在单元柱内,断层面Interface的4个顶点都在单元柱的棱上(图1),相邻顶点构成的边位于侧柱面上,称为面边。位于Interface内且与单元柱内部有交集的边或线称为内边,内边的顶点可能在面边上,也可能位于Interface内。face是Interface经过相交裁剪后保留的有效部分。最终Interface的有效部分由若干face构成。

根据交点个数和位置差异,单元柱内两个不全等Interface的相交可以枚举出10种情况(图6)。

图6 单元柱内Interface间相交示意图Fig.6 Intersection between two Interfaces in the cell column

从图6可以得到两个Interface相交的特点:①交点一定在单元柱的侧面或者棱上;②交点是两个Interface在单元柱同一侧面上的面边交点;③交线是交点顺次连接而成;④两个顺次连接的交点形成的边可以是内边或者面边。根据以上特点,单元柱内Interface求交裁剪步骤如下:

(1)根据单元柱内断层的空间关系二叉树中序遍历,新遍历的Interface(记为newInterface)和所有已经完成遍历处理的Interface(记为oldInterface)进行面边求交(图7a,b),newInterface每个面边被oldInterface递归打断成多段;

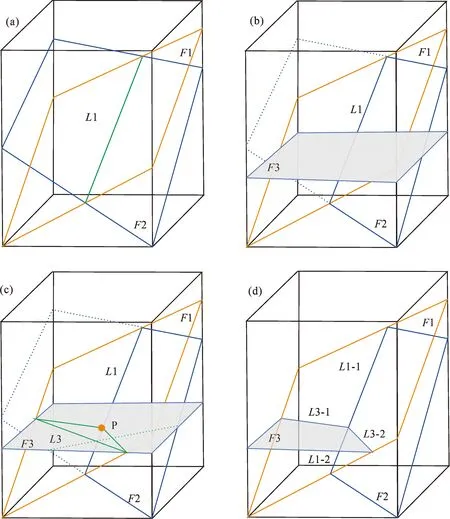
图7 单元柱内Interface相交裁剪(F1切割F2和F3,F2在F1下方,F3在F1上方): (a) F2为newInterface, F1为oldInterface; (b) F3为newInterface,L1为F1和F2的有效内边interiorEdge,L2为F2的有效面边段;(c) L3为F3和F1相交的内边,虚线为无效的内边和面边段,P为L1和F3交点Fig.7 Interface cutting in a cell column (F1 cut F2 and F3, F2 below F1, F3 above F1): (a) F2 is the newinterface, F1 is oldinterface; (b) F3 is newinterface, L1 is the valid interior edge of F1 and F2, L2 is the valid face edge segment of F2; (c) L3 is the interior edge of the intersection of F3 and F1, the dashed line is the invalid interior and face edge segments, and P is the intersection of L1 and F3

(2)判断newInterface面边的每个分段与oldInterface的空间上下关系是否满足newInterface和oldInterface的空间上下关系,不满足的面边段被剔除,满足的段为有效面边段,如图7bF2的面边处理;(3)将newInterface与oldInterface的面边交点依次连接形成内边,并剔除与面边重合的内边,如图7a内边L1。内边实际为newInterface和oldInterface的交线;

(4)将oldInterface上有效内边与新的内边在XY投影面上计算交点,记为P(图7c),内边相应被打断为多段;

(5)判断内边的每个分段与oldInterface的空间上下关系是否满足newInterface和oldInterface的空间上下关系,不满足的内边段被剔除,满足的段为有效内边;

(6)使用深度优先遍历将所有有效的面边段和内边段构成封闭的最小环,即为newInterface相交处理后的有效曲面(图7d)。

单元柱内所有Interface重复以上步骤进行。处理完成后,将隶属同一断层的Interface处理后的有效曲面拼接起来,进行Delaunay三角剖分生成相交裁剪后的三角网化断层面,进入后处理流程。

4 实验分析

利用Visual C++2019实现了本文方法,测试环境为CPU R7 5800H,16G内存和64位微软Windows 10操作系统。首先利用花状构造断层数据进行测试,并与SKUA—GOCAD 19进行了对比;然后利用煤矿三维地震断层解释数据进行验证。

4.1 对比测试

花状构造的断层网络测试

数据中有8个断层(图8a),其中,F1为主断层,4个分支断层F2、F3、F4、F5与F1相交,F2切割断层F3、F8,F5切割其他与之相交断层。基网格分辨率为1002和20002,利用二维薄板样条插值算法逐一构建网格化断层曲面,并根据断层建模总体流程进行自动化处理。得到建模结果如图8所示,断层网络切割处理结果符合断层组合关系,基网格分辨率越高,曲面光滑性越好。

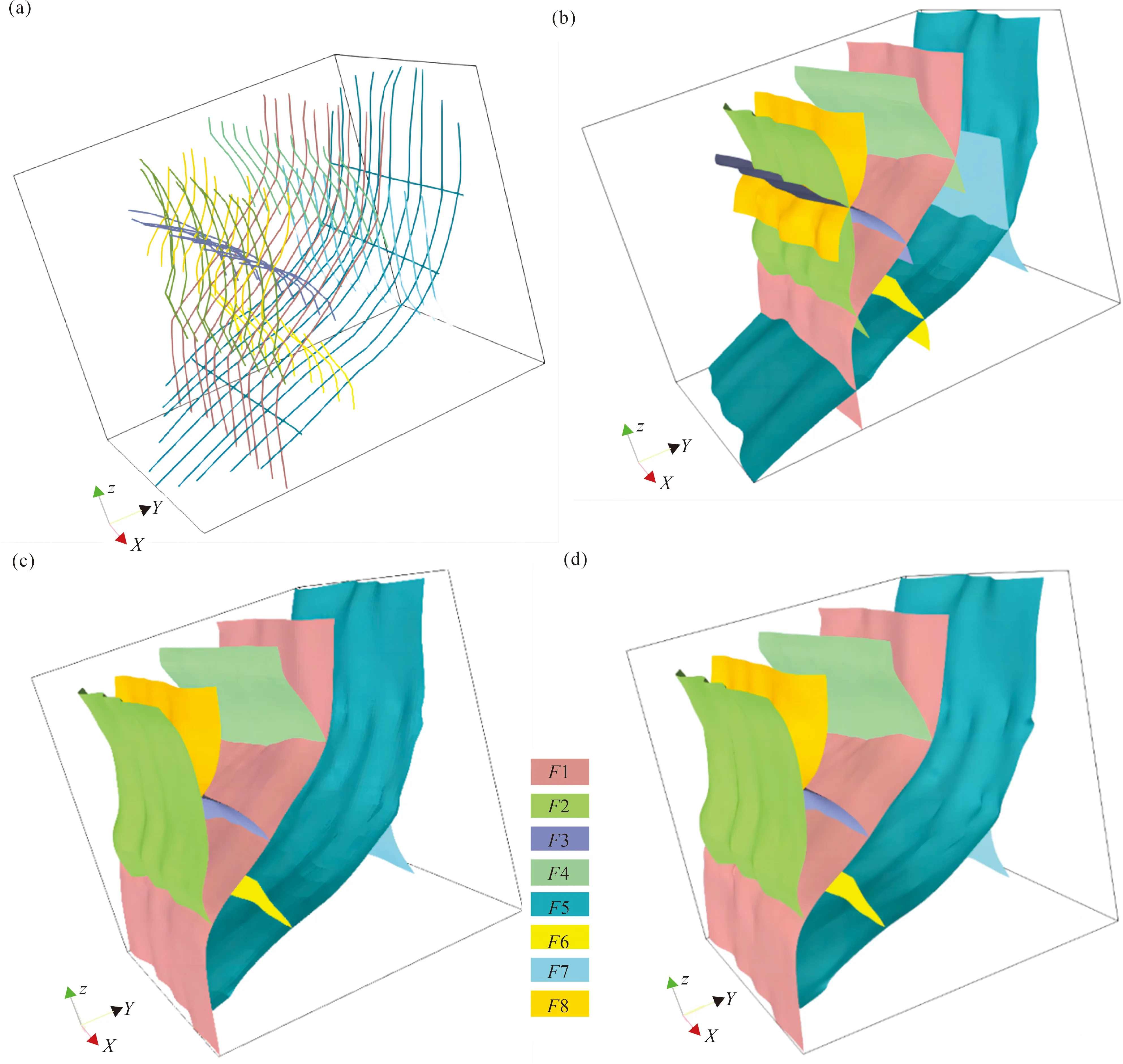
图8 花状构造断层建模:(a) 源数据:断层棱边;(b) 单个断层面生成结果;(c) 基网格分辨率1002的结果;(d) 基网格分辨率20002的结果Fig.8 Flower structure fault modeling: (a) source data: fault edges; (b) fault surface; (c) results of base grid resolution 1002 and (d) results of base grid resolution 20002

以此花状构造数据为测试数据,对比本文方法与SKUA—GOCAD 2019在建模流程和处理结果上的差异。在SKUA—GOCAD 19中利用Structural Modeling功能,输入图8a中8个断层的源数据,采用DSI空间插值算法生成断层面,设置断层间的主辅关系,得到建模结果如图9a所示,结果中断层F1和F2以及F2和F3的断层关系未能正确处理。利用GOCAD的Edit Contacts交互式对建模结果进行修正,最终得到断层切割关系正确的模型效果如图9b所示。该测试表明,相比SKUA—GOCAD断层建模方法,本文方法具有较好的算法稳定性,能够减少交互过程,提高断层建模的自动化程度。

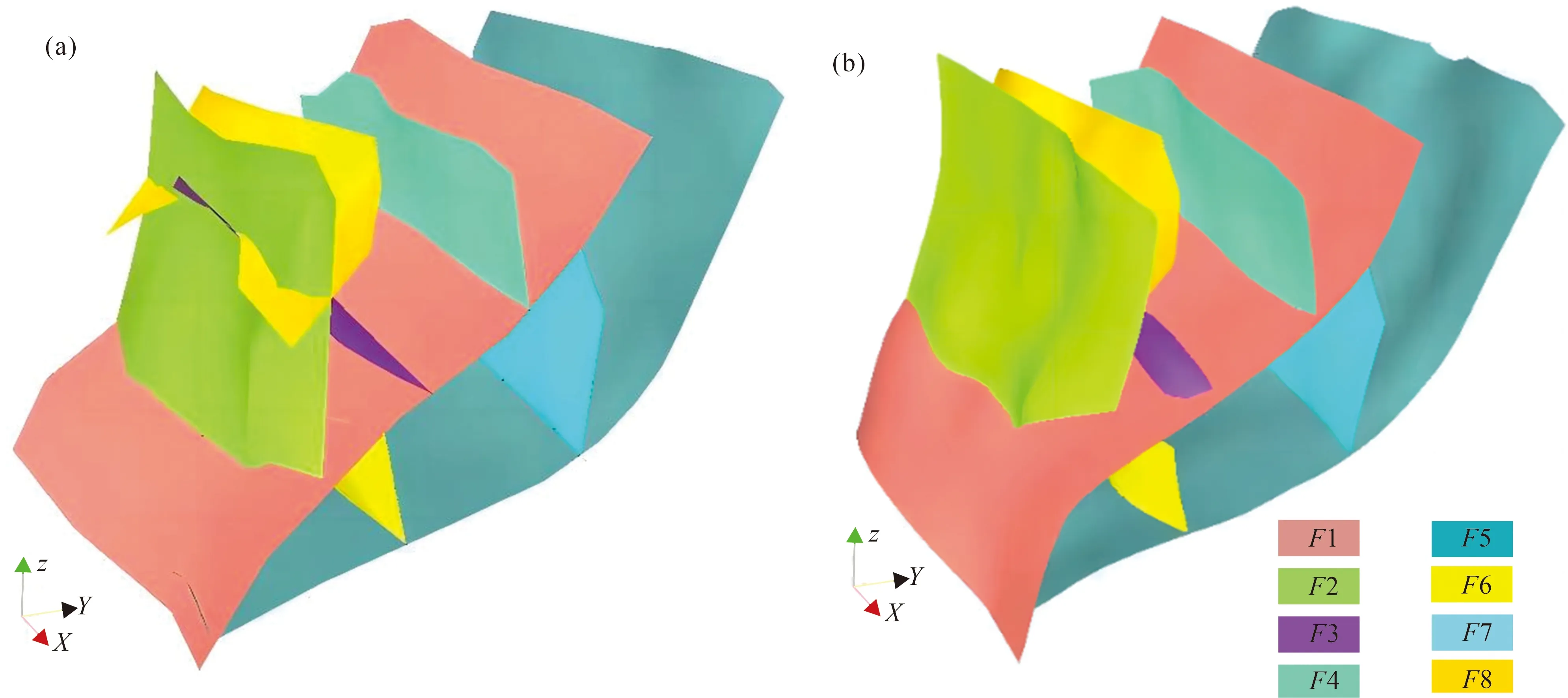
图9 SKUA—GOCAD2019花状构造断层建模结果: (a)直接建模结果; (b)交互修正断层边界Fig.9 Flower structure fault modeling result in SKUA—GOCAD2019: (a) direct modeling results; (b) interactive corrected fault boundaries

仍以花状构造数据为测试数据分析基网格分辨率对建模性能的影响。在相同测试环境下记录不同分辨率下的断层建模所需时间,结果如表1所示。从测试结果可以看出,对于地质模型基网格分辨率5002,本文方法在180 s内运行,可以满足一般建模性能需求,但对于高分辨基网格,建模耗时在分钟和小时数量级,还需进一步提升建模效率。

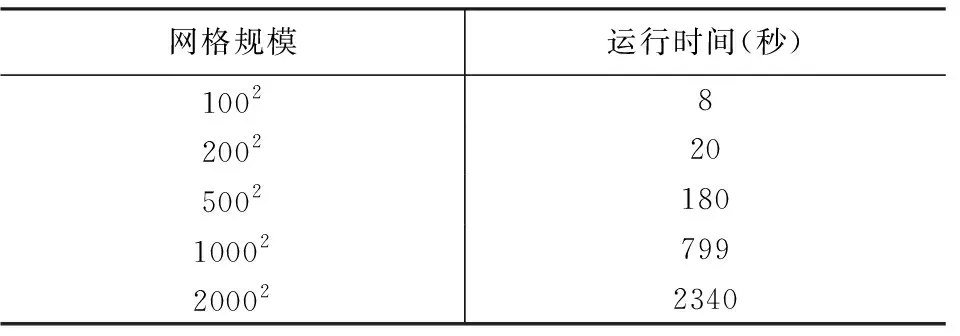
表1 不同基网格分辨率下的断层建模运行时间Table 1 Running time of fault cross-cropping at different base grid resolution

4.2 真实数据

根据某煤矿三维地震断层解释数据,选取了具有复杂切割关系的9个断层,断层输入数据如图10a所示,其中,断层DF1切割断层DF0、DF2,断层DF5切割断层DF4、DF6、DF7、DF8。基网格分辨率为5002,利用二维薄板样条插值算法逐一构建网格化断层曲面,并根据断层建模总体流程进行自动化处理。建模结果如图10c所示,断层网络切割处理结果符合断层关系,如图10d中断层DF5切割断层DF4、DF6、DF7、DF8的处理结果正确。

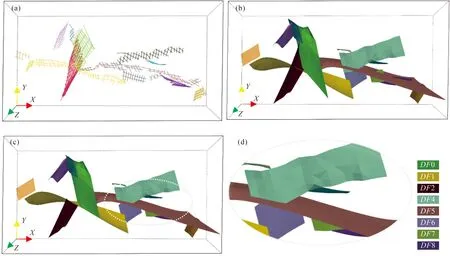
图10 某煤矿断层网络建模:(a) 源数据:断层棱边;(b) 单个断层面生成结果;(c) 断层建模结果;(d) 局部放大图Fig.10 Fault network modeling in a coalmine : (a) source data: fault edges; (b) fault surface; (c) fault modeling results; (d) local magnification plot

5 结论

针对复杂断层面切割裁剪处理算法稳定性以及断层建模流程自动化等问题,笔者等提出了基于规则网格的复杂断层网络处理与自动化建模的方法和流程,详细讨论了基于网格化的断层网络模型形式化理论表达、建模流程中的断层网络空间关系构建以及相交裁剪处理算法等核心步骤。通过基于网格化的断层网络模型形式化表达和Interface定义,将断层面建模转化为在基网格单元柱内根据断层空间关系进行Interface的求交和裁剪处理,该过程具有较好的算法稳定性。利用断层的削截主辅关系构建断层间空间关系,通过空间关系二叉树和相交关系表管理所有断层的空间关系,按照统一的流程进行断层切割裁剪和后处理,最终得到符合断层关系的建模结果。

测试验证表明,本文方法可以有效处理多条互相切割、主辅关系复杂的断层网络,具有较好的算法稳定性;通过与SKUA—GOCAD断层建模方法对比,能够减少交互过程,提高断层建模的自动化程度。

本文方法缺点和不足为:① 不能处理多值断层曲面,如S型断层曲面和和直立或近直立断层;② 断层空间关系需要严格的空间上下关系, 故不能处理X型断层组合;③ 基于基网格的断层表达是一种拟合方法,断层面的精度依赖基网格分辨率;④ 由于采用规则网格,在高分辨率基网格上,建模性能低;⑤ 最终构建的断层不规则三角形网格质量还比较差,没有进行网格优化处理。

本文方法的后续研究可以采用自适应基网格和并行处理提升建模性能,也可以将基网格由规则网格推广到三角形网格,提高基于GTP和主TIN等地质建模方法的自动化水平。