复合板压力容器内件受力有限元分析

李小虎

（森松（江苏） 重工有限公司， 上海 200135）

近些年来， 金属复合材料得到快速发展和广泛应用， 有效解决了处理含腐蚀性介质化工生产装置中压力容器设备制造成本高的问题。 应用金属复合材料制造的塔器、 反应釜等都有内件 （塔盘、填料、挡板等），内件需要焊接在压力容器上，当复合板材料中含有钛等难溶金属时， 内件就只能焊接在复层上， 这使得焊接结构的受力变得尤为复杂［1-8］。

目前， 针对这类复合板设备进行的受力研究主要在复层参与的强度计算方面［9-12］，设备内件的设计则主要是考虑内件的支撑载荷。其中，通过计算剪切力进行的焊脚设计和研究， 在很多情况下并没有详细考虑设备内压的影响［13-14］。 这种内件承载计算不考虑内压影响的计算方法是否安全是值得深入研究的，比如，很多高压反应器，在运行阶段， 设备的总体薄膜应力被控制在0.67 倍基层材料屈服强度以下，会不会存在这样的情况，即在这个应力水平下复层的应力已经超过其屈服值而失去进一步承载内件载荷的能力。 或者另一种情况，即复层没有屈服，但复层由于内压作用而产生的薄膜应力影响了其上焊接内件的外部承载能力。带着上述问题，文中对焊接在复合板复层上的内件进行受力分析， 评价内件在同时承受内压和外载荷条件下的承载能力， 并将之与无内压情况进行对比分析，总结其受力特点和作用原理。

1 复合板与内件焊接结构有限元模型

1.1 几何模型

复合板与内件焊接结构有限元分析几何模型涉及的压力容器内径为4 000 mm， 复合板基层厚度为40 mm，复合板复层厚度为4 mm，内件厚度为10 mm，内件宽度为150 mm。 内件与复层焊角打磨圆角半径为10 mm。 容器基层材料为SA-533 A CL2,复层及内件材料为SA-240 316L。 容器设计温度为250 ℃，此温度条件下2 种材料的基本属性参数见表1。

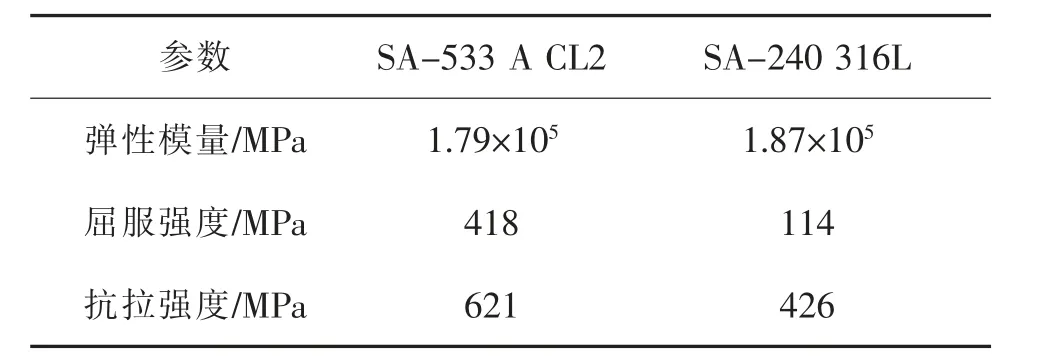
表1 容器与内件材料基本属性参数

1.2 有限元模型及网格划分

应用ANSYS 软件进行分析。复合板筒体结构具有对称性，建立轴对称模型并进行模型网格划分。 模型中，复层划分为3 层网格，基层划分为8层网格，内件厚度方向7 层网格。有限元模型及网格划分见图1。

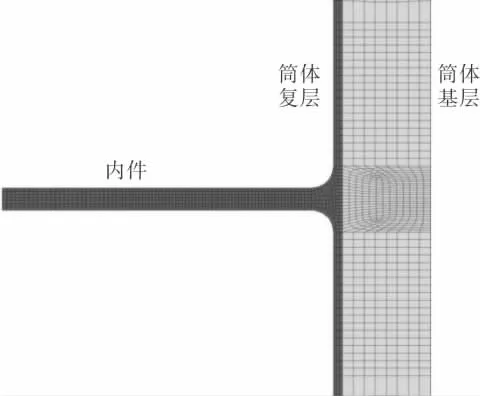
图1 复合板内件模型及网格图

2 内件受力理论基础及分析条件

2.1 理论基础

本文主要的研究重点是复合板复层上内件在承受内压和外载荷共同作用下的受力特点。 大多数情况下，内件与复层焊接会产生明显的局部位置塑性变形， 此时运用线弹性理论进行分析已经无法准确模拟其受力特点， 需要采用弹塑性理论进行分析［15］。

弹塑性分析又分为理想弹塑性分析和真实弹塑性分析， 其最大的区别在于真实弹塑性分析需要提供材料的真实应力-应变曲线，而理想弹塑性分析仅需要弹性模量和屈服强度参数。 相比于真实弹塑性分析， 理想弹塑性分析既能充分考虑材料进入屈服后的应力重分布， 又能解决大部分材料无法提供真实应力-应变曲线的问题，因此本文采用理想弹塑性分析进行计算。

2.2 分析条件

内件受力分析分为2 步进行， 第一步为静态分析，即将外部载荷设置为一个确定的值，考察内压变化对内件受力的影响， 内压变动范围设定为0～9 MPa。第二步为动态分析，在第一步的基础上添加外部载荷变化， 外部载荷p 随时间t 的变化关系式见式（1）。

式中：p 为内件端部竖直外载荷的数值， 单位MPa；t 为加载时间的数值，单位s。

3 内件受力计算结果及原因分析

3.1 静态载荷分析

3.1.1 应力分布

按照所定分析条件进行的有限元模拟分析结果表明，在设备内压和竖直载荷的共同作用下，复合板复层在较高内压下达到了整体屈服， 而且最大应力维持在材料屈服强度不再增加， 而基层材料始终处于弹性状态。 其中，内压8 MPa、竖直载荷0.65 MPa 条件下，复合板及内件焊接结构应力分布云图见图2。

图2 复合板及内件焊接结构应力分布云图

3.1.2 应变分布

图2 中复合板及内件焊接结构对应的应变分布云图见图3。 从图3 可以看出，由于竖直载荷的作用，内件发生了向下的偏移，且在连接根部区域出现了较大塑性变形（1.185%）。

图3 复合板及内件塑性应变云图

3.2 动态载荷分析

3.2.1 模拟结果

在将外部载荷随时间发生的动态变化 （时间每增加1 s，竖直载荷增加0.01 MPa）纳入考虑的情况下， 考察不同内压条件下内件竖直位移随时间的变化情况，结果见图4。 由于计算时间内位移跨度较大， 因此采用了对数位移图对加载前期的位移特点进行详细表示。

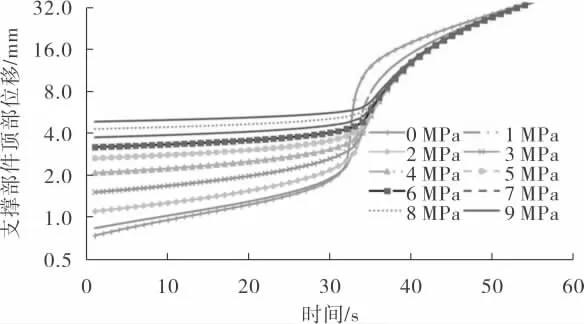
图4 支撑件顶部位移对数图

评价内支撑件的承载能力是以它在相同载荷条件下的位移大小来判断的， 基于此可以将图4的0～9 MPa 内压加载位移曲线按照时间和位移划分为3 个特征阶段，①弹性阶段（0～30 s）。 ②屈服加速阶段（30～40 s）。 ③位移趋同阶段（40～50 s）。

3.2.2 弹性阶段

以从图4 提取的部分数据（表2）为例进行内件承载能力的分析。 由表2可以知道，在内件竖直载荷增加0.1 MPa 条件下，0 MPa 内压时内件端部位移增加了0.217 mm，9 MPa 时端部位移仅增加0.143 mm；在内件竖直载荷增加0.3 MPa 条件下，0 MPa 内压时内件端部位移增加了1.112 mm，9 MPa 时端部位移仅增加0.769 mm。 总之，弹性阶段主要有2 个特点，①压力越低位移越小，即压力越低承载能力越好。②随着竖直载荷的逐渐增加，压力越低位移增幅越来越大， 低压高承载能力的特性越来越不明显。

表2 不同外载荷增量和不同筒体内压条件下内件端部位移增量 mm

3.2.3 屈服加速阶段

以图4 中0 MPa 内压曲线为例进行内支撑件承载能力的分析， 可以看出， 材料进入屈服后，0.01 MPa 的载荷增幅就会使位移显著增加 （由2.47 mm 增至7.073 mm）， 但随着筒体内压的提高， 这种屈服加速现象逐渐减弱。 材料发生屈服时0.01 MPa 载荷增量下内件端部位移情况见表3。

表3 材料发生屈服时0.01 MPa 载荷增量下内件端部位移 mm

从表3 可以知道， 内压0 MPa 下位移增量为4.603 mm，内压9 MPa 下位移增量仅为0.261 mm。同时，在此阶段，内件位移量出现反转，逐渐变成内压越高位移越小， 最大位移出现在0 MPa 内压工况下，内压0 MPa 和0.64 MPa 竖直载荷时的总位移为10.257 mm，内压3 MPa 及0.64 MPa 竖直载荷时的总位移仅为4.088 mm， 两者相差1.5倍以上。总之，在屈服加速阶段，内件根部发生屈服，且随着竖直载荷进一步增加，屈服位移出现加速。

3.2.4 位移趋同阶段

以内件承受1 MPa 坚直外载荷时产生的坚直位移为例进行内支撑件承载能力的分析，模拟在内压0～9 MPa 下内件产生的的竖直位移，所得结果几乎均大约为68 mm。 总之，在位移趋同阶段，竖直方向外载荷进一步增加，内压引起的强化承载效果逐渐减弱。

3.3 原因分析

3.3.1 概论

内件在端部竖直外载荷及内压作用下的变化规律主要由以下3 个方面决定， ①内件根部区域截面上屈服区的占比率。 更大的屈服区占比率意味着弹性区域的进一步减少， 为了承载相同的负载增量，需要更大的变形来实现。②筒体承压会产生表面拉力， 这对内件承受竖直载荷而产生的下沉弯矩具有一定的抵抗作用。 ③由于复合板基层的存在，即使在内件屈服后，基层仍然能够起到一定的支撑作用。基于此，内件承压条件下的表现需要分情况进行具体分析。

3.3.2 情况1

情况1 为不承受内压的情况， 对应的内件受力分析示意图见图5。 当图5 中的内件承受向下的坚直外载荷时， 会在内件根部形成一个上方受拉、下方受压的线性应力梯度（图6），当图5 中的内件承受的向下外载荷变大时， 图6 的应力梯度会逐渐变大，然后在表面首先形成屈服区域，并向中间扩展，最后整个厚度截面达到屈服（图7）。 图5 中，F 为内件端部载荷，A-A 为截面位置。 图6、图7 中，Sy为材料屈服限，H 为内件截面沿厚度坐标（从下至上），S 为应力。

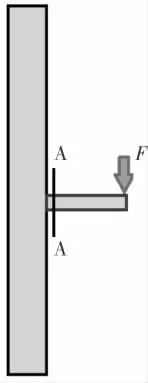
图5 非受压内件受力分析示图

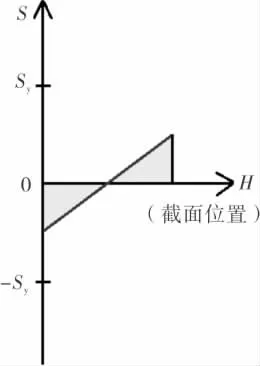
图6 未达到屈服时截面应力示图

图7 达到屈服时截面应力示图

3.3.3 情况2

情况2 为承受内压的情况， 对应的内件受力分析示意图见图8。 图8 中内件的根部会存在一个由内压引起的预紧力（图9），这时再增加竖直外载荷， 内件根部顶层会首先因为内压和弯矩的应力叠加而达到屈服， 此屈服还会由于底部2 种应力方向相反而延迟出现（图10），这是受内压和非受内压最主要的区别。 因此，在初始阶段，对于非受压筒体而言，竖直外载荷较小，内件根部仍然处于弹性状态，所以位移值最小。而对于受压情况下的内件而言， 顶部存在的应力叠加使之更容易到达屈服，因此初始位移较大。 图8 中，p 为筒体内压。 图9 和图10 中，S1为纯内压下应力，S2为截面底部应力。

图8 受压内件受力分析示图

图9 内压预紧初始截面应力图

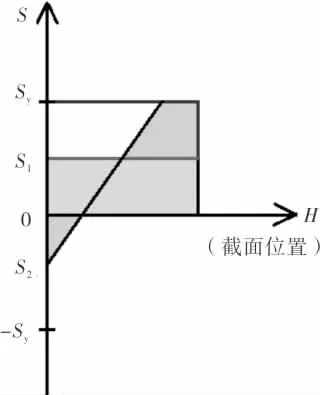
图10 顶部表面屈服时截面应力图

3.3.4 情况3

情况3 为， 内件随着内压的提高表现的屈服特点越来越不明显情况。 对于未受内压的内件而言，在整个截面到达屈服后，位移由于失去进一步承载能力而迅速扩大， 这符合理想弹塑性材料的特点。但随着内压提高，这种屈服特点会越来越不明显， 图4 中以内压8 MPa 为特征的曲线就是这种情况的典型例子。这是因为随着内压的提高，内件与筒体连接的部分在仅承受内压的条件下已经随着复合板复层一起屈服了， 因此并不存在显著的再次屈服特性。 这种情况下， Mises 应力几乎不变，一直为材料的屈服值，仅三向应力的数值发生变化，见图11。

图11 支撑件根部三向应力及Mises 组合应力图

3.3.5 情况4

情况4 为，初始内压已经导致了复层屈服，此时提供支撑的部分转移到了复合板基层上， 由于基层仍然处于弹性状态， 因此可以对内件起到支撑作用。工程上大多数复合板复层都很薄，因此这种支撑作用很明显。对于承受较高压力（导致复层屈服的情况）的内件，在整个受力过程中存在2 个阶段， 第一阶段通过三向应力的调整来达到抵抗竖直载荷，该阶段理论上限与常压状态几乎一样。当载荷进一步增加时需要依靠复合板基层支撑，该阶段位移已经很大， 支撑内件因而基本失去了原有功能，因此进一步分析的意义不大。

4 结束语

通过有限元建模和数值分析， 对内压和竖直载荷作用下的复合板设备内件的受力特点进行了总结，得到3 个结论，①在竖直载荷未引起常压容器内支撑部件发生显著屈服前 （低载荷阶段），增加内压会提高支撑部件的位移值， 而且压力越高位移就越大，即内压作用偏负面。②对于常压条件下可以计算通过的支撑件， 只要内压的增加尚未导致复合板基层屈服， 就可以认为内压和竖直载荷的共同作用不会导致结构大变形而被破坏。 如果内件要求的装配精密度更高， 建议根据实际结构情况， 采用可以考虑塑性变形的分析设计方法来详细设计。 ③对于结构完全相同的支撑件和设备筒体， 内压的增加并不会导致支撑部件最大承载能力降低。相反，高内压情况下支撑件的显著屈服阶段更不明显且位移更小，更平稳。