基于柔索并联的细长杆件吊装减摇系统动力学分析与试验研究
孙茂凱, 王生海, 韩广冬, 关 婕, 陈海泉, 孙玉清
(1.大连海事大学 轮机工程学院,辽宁 大连 116026; 2. 大连船舶重工集团有限公司,辽宁 大连 116000)
船用起重机可完成海上货物转移、舰船补给以及水下机器人的布放回收等工作,是海洋工程领域的核心装备之一。然而,由于船舶的非线性动基座激励,加之海上风浪流等因素影响以及起重机本身的欠驱动特性,吊重的摆动是不可避免的。自20世纪80年代以来,很多学者对船用起重机吊重防摆问题开展了大量研究。
Baptista等[1]早在20世纪90年代提出一种新的滑轮-刹车机械防摆装置,这种机械防摆装置被称之为马里兰索具,绳索与滑轮之间的摩擦控制技术简单,控制系统也有较强的鲁棒性。Arker等[2]提出采用RBTS(rider block tagline system)进行船用起重机吊重摆动的主动控制,但未进行相关动力学建模,同时其机械机构会影响起重机的有效作业范围。在电子式减摇方面,Singhose等[3-5]采用输入整形技术来抑制陆用起重机吊重的摆动,并先后设计出SI (specified-in-sensitivity)和RM (reduced-modification)等输入整形器。Ku等[6]采用PD(proportion differentiation)控制器实时控制绳索的张力,搭建了1∶100浮吊缩比模型,通过仿真分析和试验验证了吊重防摆效果。Henny等[7-8]针对船舶升沉、横摇以及纵摇3自由度运动的情况,设计位置时延反馈控制器根据角度测量实时输出主吊臂的变幅和回转信号,从而实现对吊重面内角和面外角的控制。Sun等[9]针对起重机双摆系统提出一种自适应减摆控制方法,通过仿真分析发现自适应减摆控制方法可以有效消除小车运动而引起的双摆现象。孙宁等[10]针对有双摆效应的起重机系统提出了一种新型的鲁棒控制策略,有效消除了吊钩和负载的两级摆动,并通过试验验证了所提控制器的有效性。王鹏程等[11]对一种回转式船用起重机系统,采用拉格朗日方法建立动力学模型,考虑了船体受海浪作用产生的6自由度运动对起重机系统状态的影响。訾斌等[12]对双起重机柔索并联作业情况,运用虚功原理和运动学关系矩阵建立了双起重机系统的动力学模型。Wang等[13]研究了细长杆件这类双摆系统起吊全程的防滑和防摆控制问题,相关研究成果提高了相关作业的安全性和效率。王生海等[14]提出一种三绳牵引机械防摆装置,设定的恒张力控制方法相比于无防摆时的面外角和面内角分别减小达92%和69%以上,同时陈海泉等[15]对该装置的张力进行仿真和试验研究。近年来,海上补给、风电安装、管线吊装等作业越发频繁,其中常涉及细长杆件类结构物的吊装,这种吊装作业往往效率低、风险大,然而目前针对动基座激励下细长杆件动力学及运动补偿控制的研究还几乎处于空白状态。
本文在前期机械式防摆装置相关研究工作基础之上[16],建立了船舶动基座激励和多柔索约束条件下细长杆件双摆系统动力学模型,并进行了动力学仿真分析,同时在细长杆件吊装试验台上进行试验验证,试验结果表明细长杆件吊装减摇装置对动基座激励下的细长杆件双摆系统有一定的减摇控制效果,相关的研究成果有望为实际工程提供关键技术支撑。
1 细长杆件吊装减摇装置结构及控制原理
1.1 细长杆件吊装减摇装置控制原理
如图1所示,细长杆件吊装减摇装置吊臂上布置有3个减摇臂和3根减摇索,并且3根减摇索的末端汇聚于新型吊钩处,三者形成一个稳定的力三角形;通过实时采集吊装减摇装置的起升和变幅动作信号、吊重摆角信号和减摇索张力信号,采用同步柔顺控制策略,来控制减摇索的收放,并保证减摇索上的张力始终处于设定范围内,从而实现细长杆件类结构物摆动的抑制。

1.船舶运动模拟装置; 2.细长杆件类结构物; 3.新型吊钩; 4. 三根减摇索I; 5.减摇臂I; 6.主吊索; 7.三根减摇索III; 8. 三根减摇索II; 9.减摇臂II; 10.起重机塔筒; 11.减摇臂III; 12.起重机主吊臂。图1 细长杆件吊装减摇装置三维结构Fig.1 Three-dimensional structure of the anti-swing device for slender payload
2 细长杆件吊装减摇系统模型
为了方便研究细长杆件吊装减摇系统的运动规律,在建模过程中做以下假设:①忽略主吊索和减摇索弹性形变以及质量;②忽略细长杆件吊装减摇系统各处的干摩擦;③吊钩为质量集中的质点、细长杆件为质量均匀分布的刚体。
2.1 运动学模型
图2为细长杆件吊装减摇系统的简图,图2中:x0y0z0为惯性坐标系;x1y1z1为船体坐标系;x2y2z2为起重机坐标系。假定吊钩为质点,细长杆件为质量均匀分布的刚体,吊钩与细长杆件的质心在空间坐标系中的坐标分别记作P1,P2;O2E为起重机主吊臂;P1D为主吊索长度记为l1;吊钩质心到细长杆件质心的距离记为l2;EF为前减摇臂;HMN和HRS分别为左右横向减摇臂,θ2y为主起升臂的变幅角度;θ2z为起重机的回转角度;θ1x和θ1y分别为船舶运动模拟装置设定的纵摇角度以及横摇角度(相对应于船舶运动的纵摇和横摇);β1,β2分别为前减摇臂以及左右横向减摇臂的夹角。起重机在实际作业时主要受船舶横摇影响比较大,因此本文只考虑了细长杆件减摇系统的面内角,定义P1在x0y0z0中的坐标为0PP1=[xP1yP1zP1]T,定义LP1F为F到P1的空间距离,其余坐标点及距离的表示方法以此类推,下文不再一一列举。

图2 吊装减摇装置简图Fig.2 The diagram of the anti-swing device
P1以及P2在起重机坐标系x2y2z2中的坐标为
(1)
(2)
其中D在起重机坐标系x2y2z2的坐标为
(3)
同时F点、N点以及S点在起重机坐标系x2y2z2坐标分别为
(4)
(5)
(6)
主减摇索P1F与辅减摇索P1N的长度分别为
(7)
(8)
当θ1的角度为0时,分别对主减摇索P1F及辅减摇索P1N的速度边界条件进行求解,对主减摇索P1F及辅减摇索P1N的长度进行求一次导,可得主减摇索P1F及辅减摇索P1N的速度



(LO2Hsinθ2y+LMNsinθ1sinθ2y+l1-LO2Dsinθ2y)·
(10)
定义Rx,Ry,Rz分别为关于x轴,y轴以及z轴的旋转矩阵,其表达式为
(11)
(12)
(13)
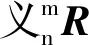
(14)
(15)
可求吊钩P1在惯性坐标系中的坐标
(16)
0P1=[0 0 0]T为O1在惯性坐标系x0y0z0中的坐标,1P2=[LxLyLz]T为O2在船体坐标系x1y1z1中的坐标,将式(1)、式(14)及式(15)代入式(16)中可求惯性坐标系x0y0z0中吊钩P1的表达式
xP1>=Lxcosθ1y+cosθ2z(LP1Dcosθ1+LO2Dcosθ2y)cosθ1y+
Lzcosθ1xsinθ1y+Lysinθ1xsinθ1y+LPDsinψo·
(cosθ1xsinθ2z-cosθ2zsinθ1xsinθ1y)+(LO2Dsinθ2y-
LP1Dcosθ1)(cosθ1xcosθ2zsinθ1y+sinθ1xsinθ2z)(17)
zP1=cosθ1xcosθ1y(-LP1Dcosθ1+Lz+LO2Dsinθ2y)-
(Lx+LP1Dcosθ1+LO2Dcosθ2y)sinθ1y+
(Ly-LP1Dsinθ1)cosθ1ysinθ1x
(18)
2.2 静力学模型
定义主减摇索P1F及两根辅减摇索P1N,P1S张力分别为F1,F2和F3,FR为主吊索P1D的张力,吊钩与细长杆件的重力之和为GP,吊钩的质量为m1,细长杆件的质量为m2,吊钩与细长杆件的质量之和为m,如图3所示,细长杆件系统无外在激励时,细长杆件以及吊钩在自身重力、主吊索张力以及3根减摇索张力的作用下保持静平衡状态。

图3 细长杆件静平衡分析Fig.3 Static balance analysis of slender payload
定义F1=[F1xF1yF1z]T,F2=[F2xF2yF2z]T,F3=[F3xF3yF3z]T,当船舶基座激励为零细长杆件不受外力作用时,主吊索P1D处于竖直状态,两根辅减摇索受力大小相等方向相反,即F2y=-F3y故只研究一侧辅减摇索的张力F2即可,在此情况下,只需要考虑面x00z0内的静平衡问题。
式中:i1x和i1z为主减摇索P1F的方向向量;i2x和i2z为辅减摇索P1N的方向向量;i3x和i3z为与P1N对称的减摇索P1S的方向向量;xF,zF,xN,zN,xS及zS的坐标可由式(4)~式(6)得知。
面x00z0内的静平衡方程为
F1x-F2x-F3x=0
(22)
F1z-F2z-F3z-mg+FRz=0
(23)
由于减摇索P1N,P1S在空间坐标系中的对称性
(24)
将式(19)~式(21)和式(24)代入式(22)以及式(23)可得
(25)
由于减摇索受拉不受压得特性可知
FRz≥0
(26)
由式(25)、式(26)可得张力F1的约束条件为
(27)
2.3 动力学模型
如图4所示,仅考虑船舶横摇激励,即细长杆件以及吊钩在面x00z0内运动,在船舶横摇激励下,细长杆件与吊钩之间存在相互作用力,吊钩受到3根减摇索的约束力作用,同时约束力对吊钩下方的细长杆件面内角的摆动也有一定的抑制效果。

图4 细长杆件动力学分析Fig.4 Dynamic analysis of slender payload
主吊索张力在x0及z0方向的分量分别为
(28)
FEx以及FEy为细长杆件在x方向和z方向上的受力,根据牛顿第二定律可知吊钩在面x00z0内的运动方程为
(29)
(30)

(31)
(32)


(33)

(34)
定义3根辅减摇索在面x00z0内的合力分别为
fx=F1x-F2x-F3x
(35)
fz=F1z-F2z-F3z
(36)
根据牛顿第二定律可得
(37)
对细长杆件进行受力可得
(38)
消掉FR可得
(39)
可求一级摆角θ1的加速度

(40)
为求细长杆件的摆角θ2,对细长杆件进行单独受力分析,并对细长杆件的质心P2取矩如图5所示,最后可求细长杆件的二级摆角θ2。
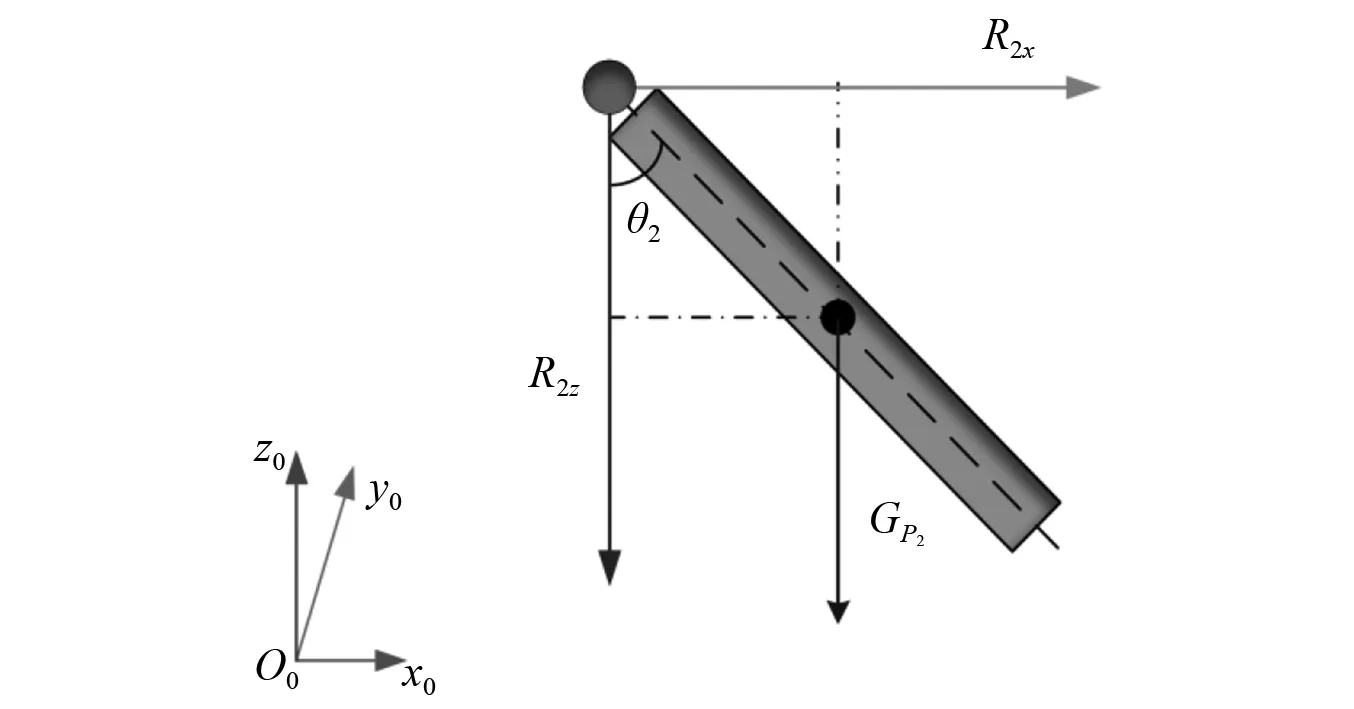
图5 细长杆件受力分析Fig.5 Force analysis of slender payload
细长杆件质心的力矩总和为
(41)
其中细长杆件质心至吊钩处的距离为l2,由牛顿第二定律可知
(42)
细长杆件的旋转轴位于吊钩处,可知细长杆件的转动惯量为
(43)
将式(42)以及式(43)代入式(41),可求细长杆件二级摆角θ2的加速度

l1l2m2cos(θ1-θ2){-fx+secθ1·
(44)
在细长杆件减摇系统的控制部分通过设定恒张力控制模型使3根减摇索的合力始终阻碍吊重的相对运动,张力设定模型如下
(45)
式中:F1s,F2s和F3s为静平衡条件下3根减摇索P1F,P1N和P1S的张力设定值;δ1,δ2和δ3为设定的张力阈值。最后通过MATLAB/SIMULINK软件对细长杆件减摇系统进行仿真分析。
3 细长杆件吊装减摇系统仿真
3.1 减摇索速度仿真
对减摇索的速度进行仿真分析,可以确定当起重机的变幅机构以一定速度进行变幅动作时,可以确定减摇索的收放速度,以此来确定各减摇索驱动机构的执行速度,因此,对减摇索的速度边界条件进行仿真,具有一定的工程意义。系统选取的参数与所搭建的试验台的实际参数保持一致,其中细长杆件吊装减摇系统的参数选取为:LOE=1.3 m,LEF=0.5 m,LOH=0.3 m,LHM=0.25 m,LMN=0.75 m,LOD=1.2 m,LOA=0.9 m,β1=0°,β2=10°,起重机的工作空间设定为:主吊索长度变化范围l1=0.2~1.4 m,起重机主吊臂的变幅范围θ2y=0°~80°。
当起重机以3 (°)/s进行变幅动作时,减摇索P1F以及P1N的速度变化趋势如图6和图7所示,减摇索P1F的速度随变幅角度和绳索长的增加呈先变大后减小的趋势,减摇索P1F速度的最大值在主吊索1 m,变幅角度为0°时取得。减摇索P1N的速度随变幅角度增大而减小,随主吊索的增大而增大,减摇索P1N速度最大值在变幅角为0°,主吊索为1.4 m时取得。

图6 减摇索P1F的速度变化趋势Fig.6 Velocity trend of the anti-swing cable P1F

图7 减摇索P1N的速度变化趋势Fig.7 Velocity trend of the anti-swing cable P1N
当起重机以0.1 m/s进行起升动作时,减摇索P1F以及P1N的速度变化趋势如图8和图9所示,减摇索P1F的速度范围在0.04~0.10 m/s,最大值在变幅角度80°,主吊索为1.4 m时取得,减摇索P1N的速度范围在0.04~0.07 m/s,最大值在变幅角度为0°,主吊索长度为1.4 m时取得。随着主吊索长度的增加,减摇索P1F呈现增加的趋势,而减摇索P1N呈先减小后增加的趋势。随着变幅角度增加,减摇索P1F呈现增加的趋势,而减摇索P1N呈先减小后增加的趋势。

图8 减摇索P1F的速度变化趋势Fig.8 Velocity trend of the anti-swing cable P1F

图9 减摇索P1N的速度变化趋势Fig.9 Velocity trend of the anti-swing cable P1N
3.2 细长杆件减摇系统仿真分析
(1)为研究恒张力控制减摇方法对细长杆件减摇系统所简化成的带约束力的二级摆是否可以有效抑制,分别在横摇θ1y=6sin(πt/3),θ1y=10sin(πt/3)条件下对有减摇措施以及无减摇措施进行仿真分析,如图10~图13所示。从仿真曲线可以看出:①由于细长杆件与吊钩之间构成的系统存在相互作用力,当无减摇措施时,θ1与θ2的摆动角度的最大值达不到设定的横摇角度;②所提的恒张力控制方法在特定工况下可以对θ1和θ2都可以实现良好的减摇效果,对θ1和θ2的平均减摇效果可达80%以上;③θ1曲线比θ2曲线更平滑是由于3根减摇索的控制力直接施加在吊钩处,而细长杆件受到吊钩以及自身摆动的作用力导致。
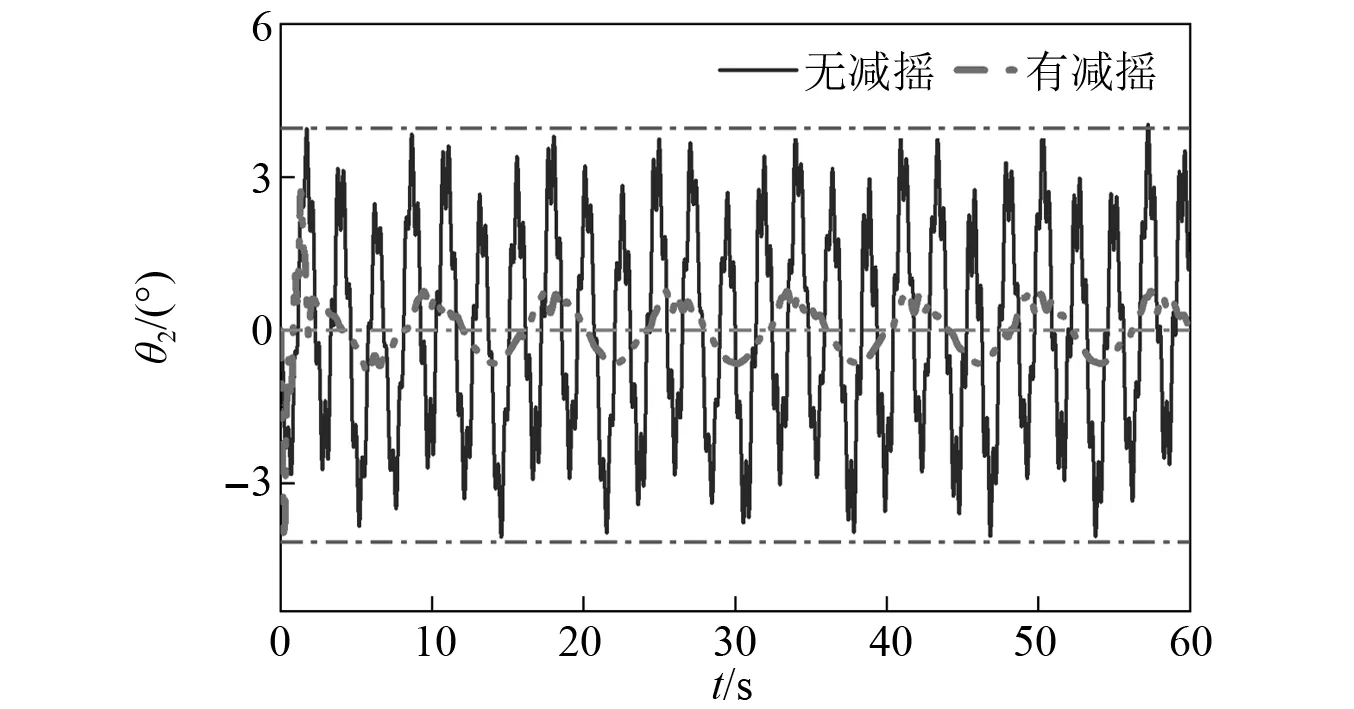
图11 θ1y=6sin(πt/3),θ2幅值变化Fig.11 θ1y=6sin(πt/3),amplitude change of θ2
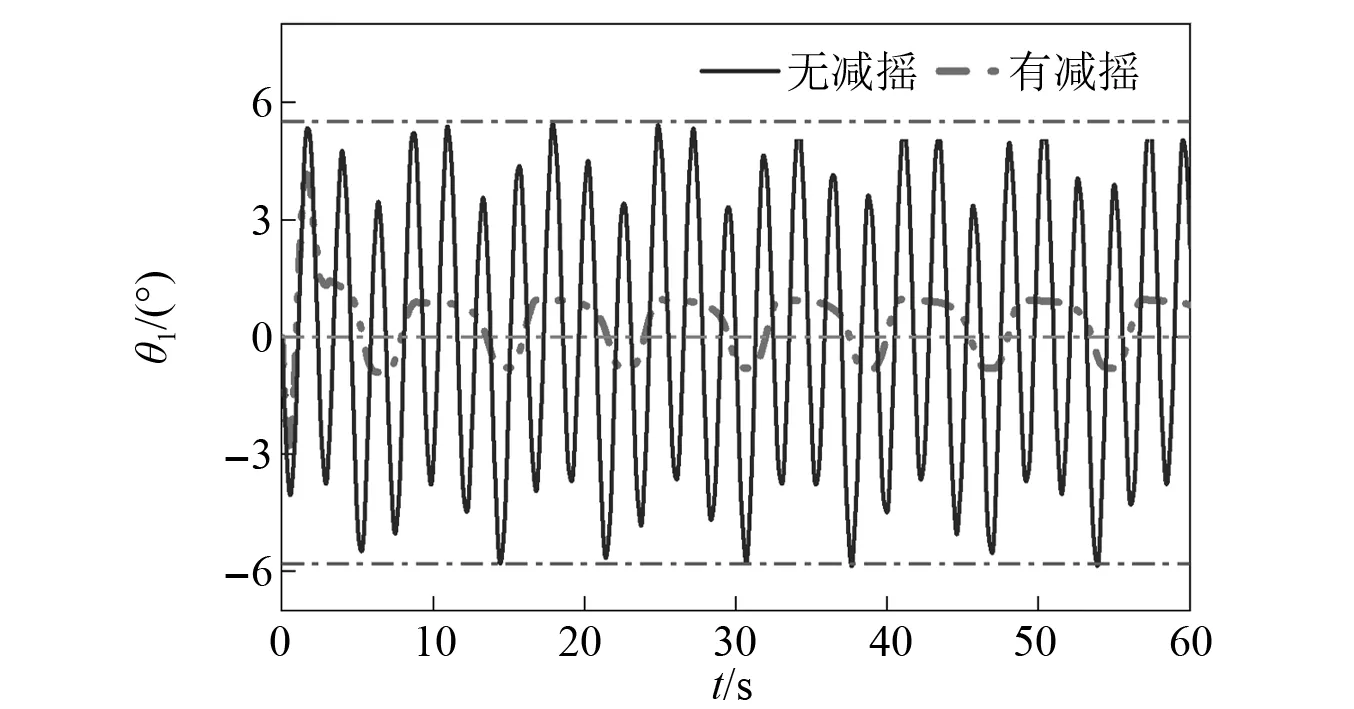
图12 θ1y=10sin(πt/3),θ1幅值变化Fig.12 θ1y=10sin(πt/3),amplitude change of θ1
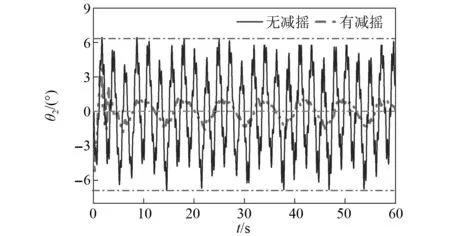
图13 θ1y=10sin(πt/3),θ2幅值变化Fig.13 θ1y=10sin(πt/3),amplitude change of θ2
(2)在横摇θ1y=6sin(πt/3)条件下分别对θ1和θ2设置初始角度,对θ1=0°,θ1=20°以及θ2=0°,θ2=20°的3种组合情况在有减摇措施和无减摇措施分别进行仿真分析,如图14~图19所示,通过仿真曲线可知:①θ1=0°,θ2=20°对比于θ1=20°和θ2=0°的情况,前者在有减摇措施下θ1和θ2的摆动可以更快的被抑制;②当设定θ1和θ2的初始角度都为20°时,吊钩与细长杆件的质心处于共线状态,在有减摇措施下θ1和θ2趋于稳定的时间以及趋势基本一致。

图14 θ1=0°,θ2=20°时,θ1幅值变化Fig.14 θ1=0°, θ2=20°,amplitude change of θ1
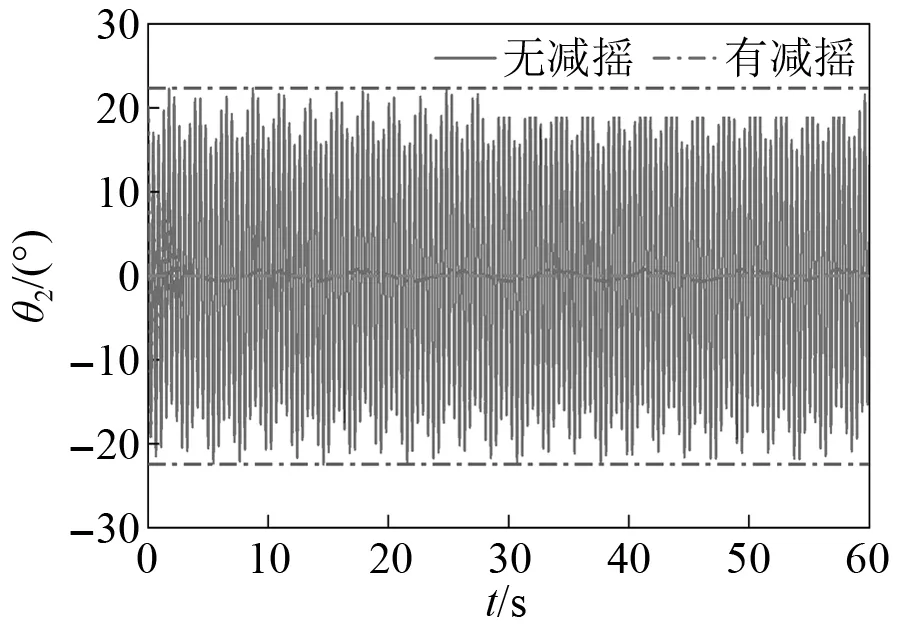
图15 θ1=0°,θ2=20°时,θ2幅值变化Fig.15 θ1=0°, θ2=20°,amplitude change of θ2
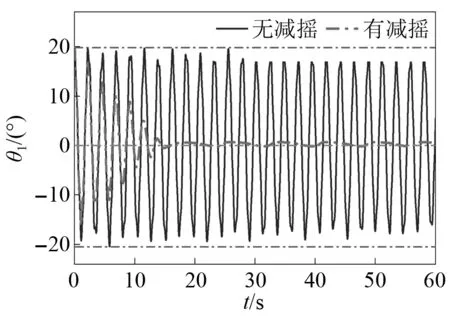
图16 θ1=20°,θ2=0°时,θ1幅值变化Fig.16 θ1=20°, θ2=0°,amplitude change of θ1

图17 θ1=20°,θ2=0°时,θ2幅值变化Fig.17 θ1=20°, θ2=0°,amplitude change of θ2

图18 θ1=20°,θ2=20°时,θ1幅值变化Fig.18 θ1=20°, θ2=20°,amplitude change of θ1

图19 θ1=20°,θ2=20°时,θ2幅值变化Fig.19 θ1=20°, θ2=20°,amplitude change of θ2
4 细长杆件吊装减摇装置试验验证
如图20所示,在吊装减摇装置试验台上开展了细长杆件吊装减摇试验,其中船舶运动模拟装置可模拟船舶六自由度运动,试验平台采用阀控液压马达驱动卷筒实现减摇索的收放动作,由于液压系统有一定的时滞性和惯性,难以实现减摇索的精确控制。在摆角的测量中,选择摆角测量装置对细长杆件一级摆角进行测量,而对细长杆件二级摆角测量则采用高码率相机采集视频,然后进行数据分析后得出。

1.船舶运动模拟装置; 2.起重机塔筒; 3.主起升臂; 4.液压站; 5.摆角测量装置; 6.减摇索; 7.细长杆件类结构物; 8.新型吊钩。图20 细长杆件吊装减摇装置试验台Fig.20 The anti-swing device for slender payload
在控制台将船舶运动模拟装置的横摇激励设置为θ1y=6sin(πt/3),细长杆件结构物的质量为10 kg,新型吊钩的质量为8 kg,细长杆件类结构物的长度为0.9 m,主吊索的长度为1 m。图21和图22为无减摇措施时仿真与试验的对比曲线,图23和图24则为吊装减摇系统介入工作时仿真与试验的对比曲线。在无减摇措施和吊装减摇系统介入工作时,θ1以及θ2的仿真曲线和试验曲线基本一致,验证了细长杆件吊装减摇系统动力学模型的正确性,由于液压系统的时滞性和惯性,仿真结果与细长杆件吊装的试验结果存在一定的误差,但仍在可接受范围内。

图21 θ1y=6sin(πt/3),θ1幅值变化Fig.21 θ1y=6sin(πt/3),the amplitude change of θ1

图22 θ1y=6sin(πt/3),θ2幅值变化Fig.22 θ1y=6sin(πt/3),the amplitude change of θ2

图23 θ1y=6sin(πt/3),θ1幅值变化Fig.23 θ1y=6sin(πt/3),the amplitude change of θ1

图24 θ1y=6sin(πt/3),θ2幅值变化Fig.24 θ1y=6sin(πt/3),the amplitude change of θ2
如图25所示,在吊装减摇系统装置原理上研发的克令吊防晃装置2021年已成功在中远海运集团2.7 万t船舶上得到示范应用,可在4级海况下完成吊重转运定位作业。细长杆件吊装减摇系统动力学分析可为细长杆件类结构物的吊装及转运提供一定的理论依据。

图25 克令吊防晃装置实船应用Fig.25 Application of anti-swing device for marine crane
5 结 论
本文针对细长杆件类结构物吊装作业困难问题,提出了基于柔索并联的细长杆件吊装减摇系统,运用机器人学和牛顿欧拉方法建立了船舶动基座激励和多柔索约束条件下细长杆件双摆系统动力学模型,研究了减摇索的收放速度、船舶运动激励下不同一级摆角和二级摆角初始值对细长杆件减摇系统摆动规律的影响,最后通过试验来验证仿真结果。
(1)论文将细长杆件吊装减摇系统简化为受约束二级摆,并在船舶动基座激励和多柔索约束条件下进行动力学建模与仿真分析。
(2)在细长杆件减摇系统仿真与试验中,在设定工况下有减摇措施相比于无减摇措施时θ1和θ2的摆动幅度均减小70%以上,通过试验说明减摇系统对细长杆件这类双摆系统也有良好的摆动抑制效果。
(3)在受约束二级摆存在初始摆角条件下,本文所提的减摇措施对细长杆件双摆系统同样有效,同时在相同初始摆角条件下θ1和θ2趋于稳定的时间以及趋势基本一致。
(4)在细长杆件吊装减摇试验台上进行试验时,θ1以及θ2的仿真曲线和实际试验曲线基本一致,验证了细长杆件吊装减摇系统动力学建模的正确性。
论文研究结果可为细长杆件双摆系统减摇控制器设计奠定一定数学基础,同时对细长杆件类结构物的吊装和转运提供一定理论依据。

