基于本征正交分解和卡尔曼滤波的结构损伤识别
杨少冲, 姚 远, 张 凯, 宋康宁, 刘家亮, 靳佳林, 马连华, 方有亮
(1. 河北大学 建筑工程学院,河北 保定 071002; 2. 河北大学 质量技术监督学院,河北 保定 071002)
由于各种环境和力学因素的影响,结构易产生一定程度的损伤。损伤传统上被定义为系统几何或材料特性的变化[1],对结构的安全性、可靠性和使用寿命产生不利影响。结构振动损伤识别技术是近年来结构健康监测领域重要的研究方向之一[2],也是结构健康监测技术的核心[3],如何实现实时、快速的在线损伤识别,是目前损伤识别技术的关键。从已有文献看,用于土木工程领域的在线损伤识别方法已取得长足的进展,但还处于起步阶段,有着较大的进步空间[4]。
本征正交分解(proper orthogonal decomposition,POD)方法是一种较为高效的模型降阶技术,该方法能在减少模型自由度的同时,对其主要特征信息进行提取,保证数值模型具有足够高的精度。该方法通过试验或数值模拟得到的响应数据,构造用于模型降阶的基向量,可以快速、准确地反映出研究对象的主要特征,实现模型降阶。由于POD方法能够在保持高精度的同时从少量的POD模态中提取结构特征,它已被广泛用于模型降阶中[5]。近年来,POD模型降阶方法在航空航天[6-7]、计算流体力学[8]、材料力学[9]等领域都得到了广泛应用,在近期的研究中,Lu等[10]全面综述了POD方法在不同领域的应用,并对该方法的发展前景进行了展望。在土木工程领域中,Eftekhar Azam等[11]研究了基于POD方法对动力结构系统降阶建模的性能,通过对快照矩阵进行奇异值分解(singular value decomposition,SVD)构建降阶模型,结果表明该方法得到的降阶模型可以达到较高的精度,且优于模态分析。
除在模型降阶方面有较高的效率和精度外,基于POD方法得到的结构本征正交模态(proper orthogonal modes, POMs),可以用于表征结构损伤的位置和程度,Galvanetto等[12]较早地利用该方法对简支梁进行了数值模拟,成功识别出损伤的程度和位置,并在之后的研究中仅利用传感器数据成功对损伤进行识别[13],而不需要较为精确的数值模型。在国内的损伤识别领域中,杨斌等[14]将奇异值分解与POD方法相结合,通过结构各单元的应力分布进行损伤识别分析,成功识别出结构的损伤及其位置;王丹生等[15]在早期利用POD方法对简支梁结构的损伤位置进行了识别,验证了该方法的有效性,并在近期的研究中,将POD方法与粒子群优化算法相结合[16],对剪切型建筑物进行损伤检测,有效地识别出不同程度的损伤。
而在利用POD方法进行损伤识别分析时,需要利用一段时间的响应构造快照矩阵进行分析,当出现损伤时,需要进行重复的训练阶段[17],因此要对传统方法进行改进,使其能够更加快速、准确地对损伤进行识别。卡尔曼滤波法(Kalman filter,KF)方法是一种以最小均方差为准则的状态最优估计法[18],根据不断采集的新数据对上一步识别结果进行修正,广泛应用于结构的各项参数识别中,它能够对系统下一步的走向做出有根据的预测,可用于在线识别。黄进鹏等[19]利用扩展卡尔曼滤波法(extended Kalman filter,EKF)对车桥耦合作用下的桥梁结构进行分析,成功识别出桥梁结构的损伤,并有一定的抗噪能力。Liu等[20]提出了一种基于未知激励的EKF方法的递归估计,在识别结构系统参数的同时,成功对未知外部激励进行了识别。然而,基于KF方法的损伤识别是一个典型的反问题,在处理大型结构时,状态向量的维数过大往往会对KF方法的计算效率产生不利的影响,也可能会导致KF方法收敛困难、识别结果不准确[21],因此考虑利用POD方法对结构进行降阶分析,可以很好地解决KF方法在处理大型结构时收敛困难的问题。
1 基于POD的动态模型降阶
本文提出的基于动态响应数据驱动的模型降阶主要是根据获取的系统动力学响应构造快照矩阵,选择一组最能够表征系统特征的标准正交基,以获取结构的主要特征。
当结构受到外部载荷的影响时,其动力响应可以用下面的运动方程来描述
(1)
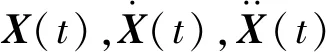
在利用POD方法进行模型降阶时,我们考虑位移响应向量X∈Rm,R为实数的集合,m为位移响应向量X的维数。对于线性系统,位移响应可以写成如下的变换形式
(2)
式中:yi为模态坐标下的位移响应,排列在列向量y中;{φi},i=1,…,m为一组标准正交基,称为POMs;φ为坐标转换矩阵,由所选取的正交基组成,表示为
φ=[φ1φ2…φm]
(3)
通常,我们仅需要保留前几阶POMs,就可以跟踪系统的演化,因此定义了式(2)的简化表示
(4)
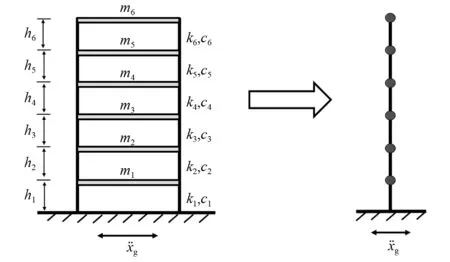
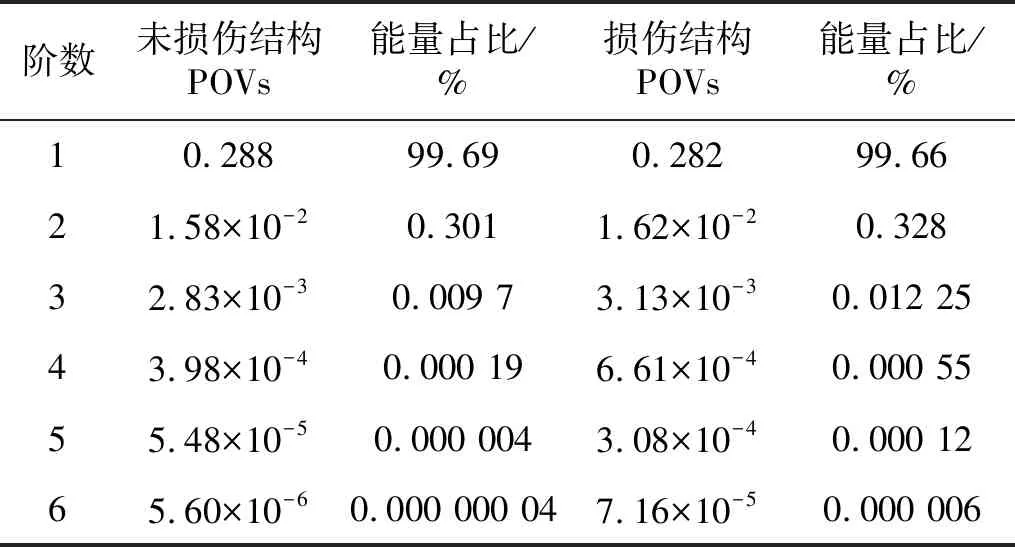
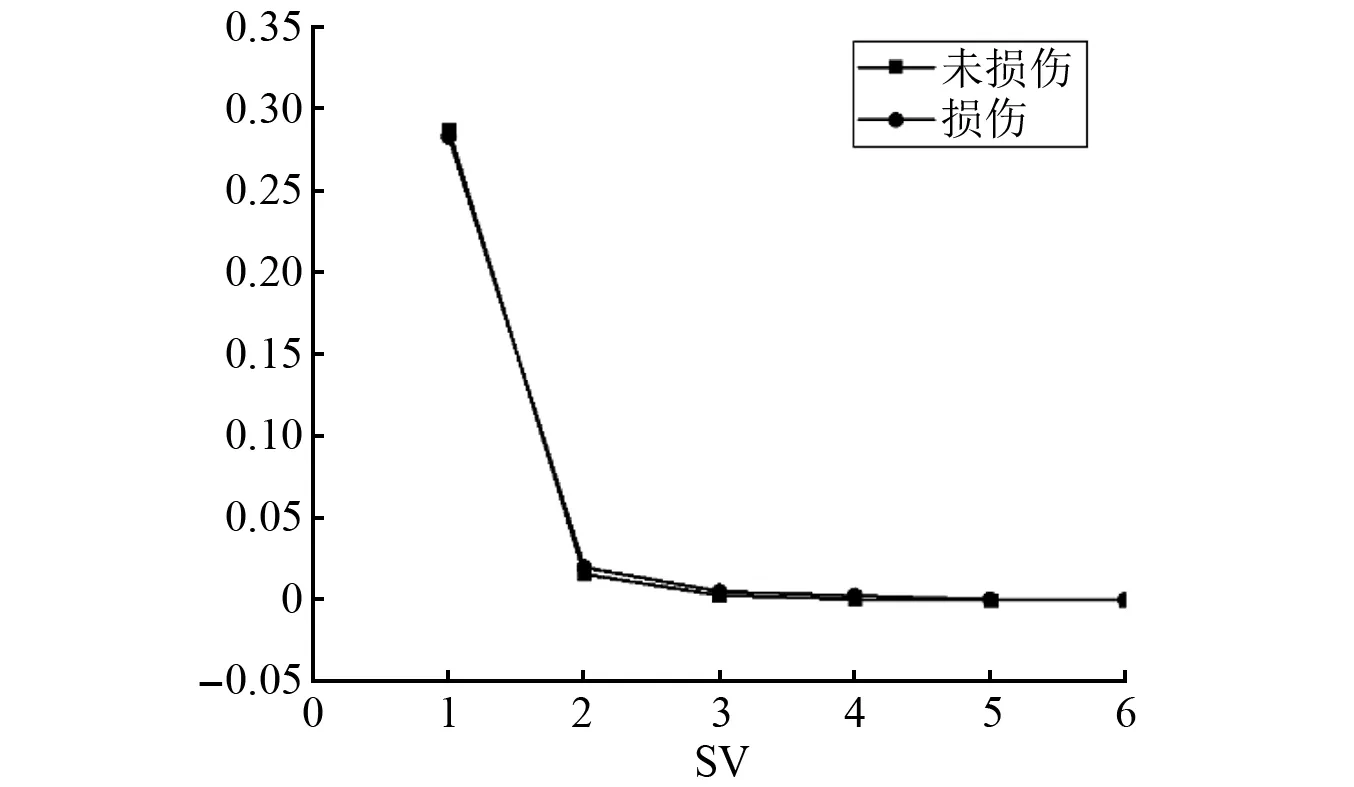
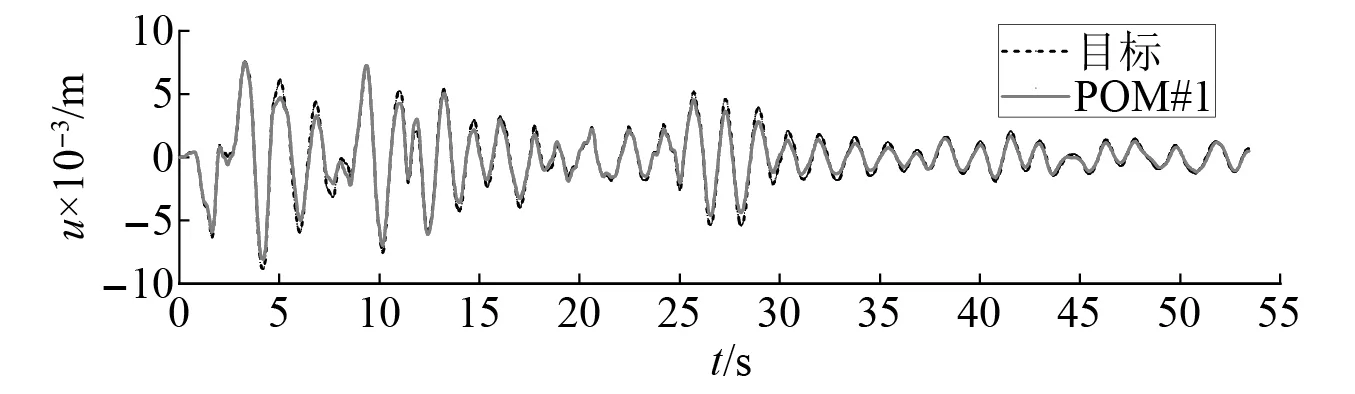
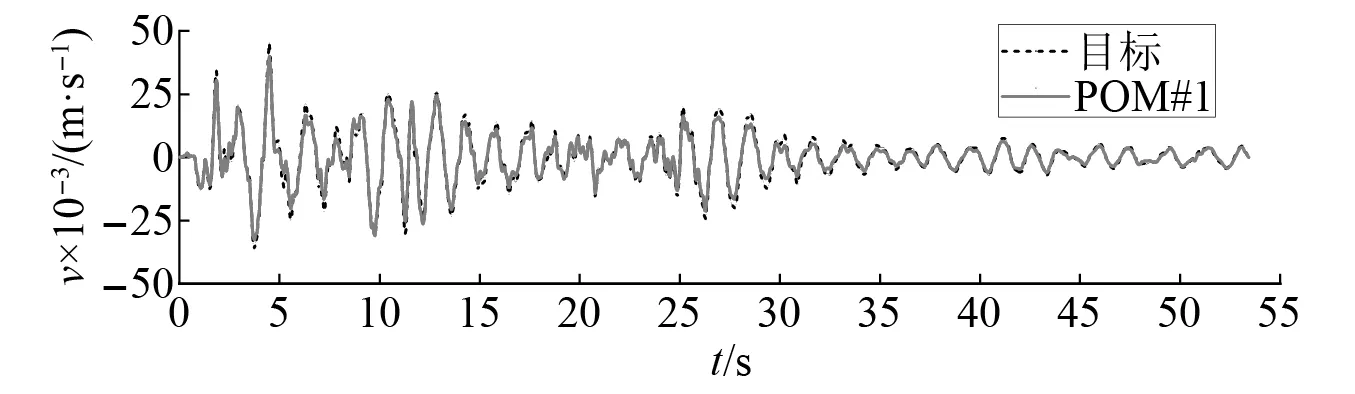
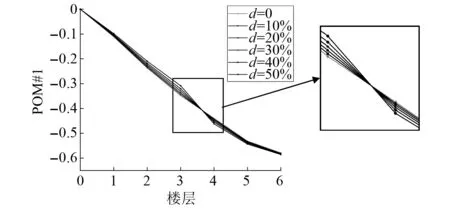
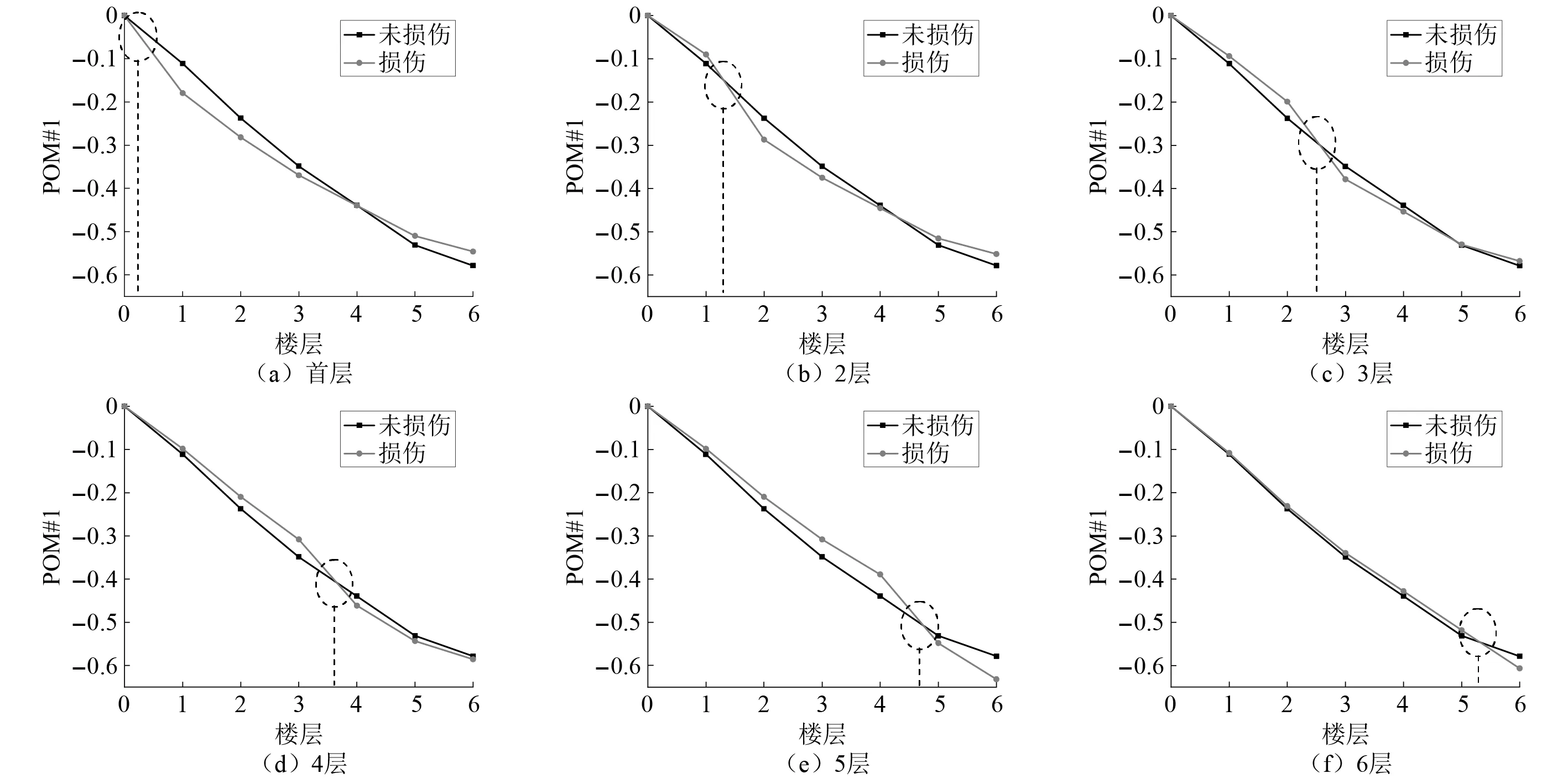
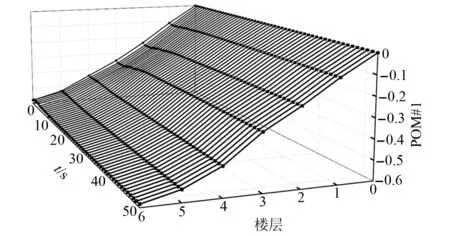
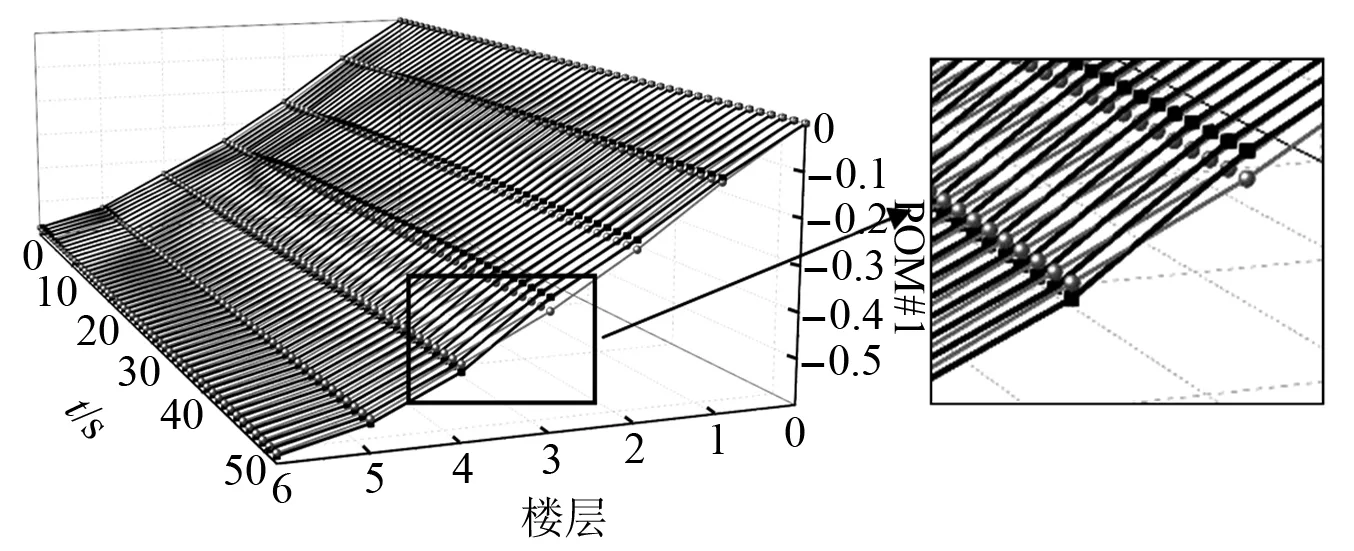
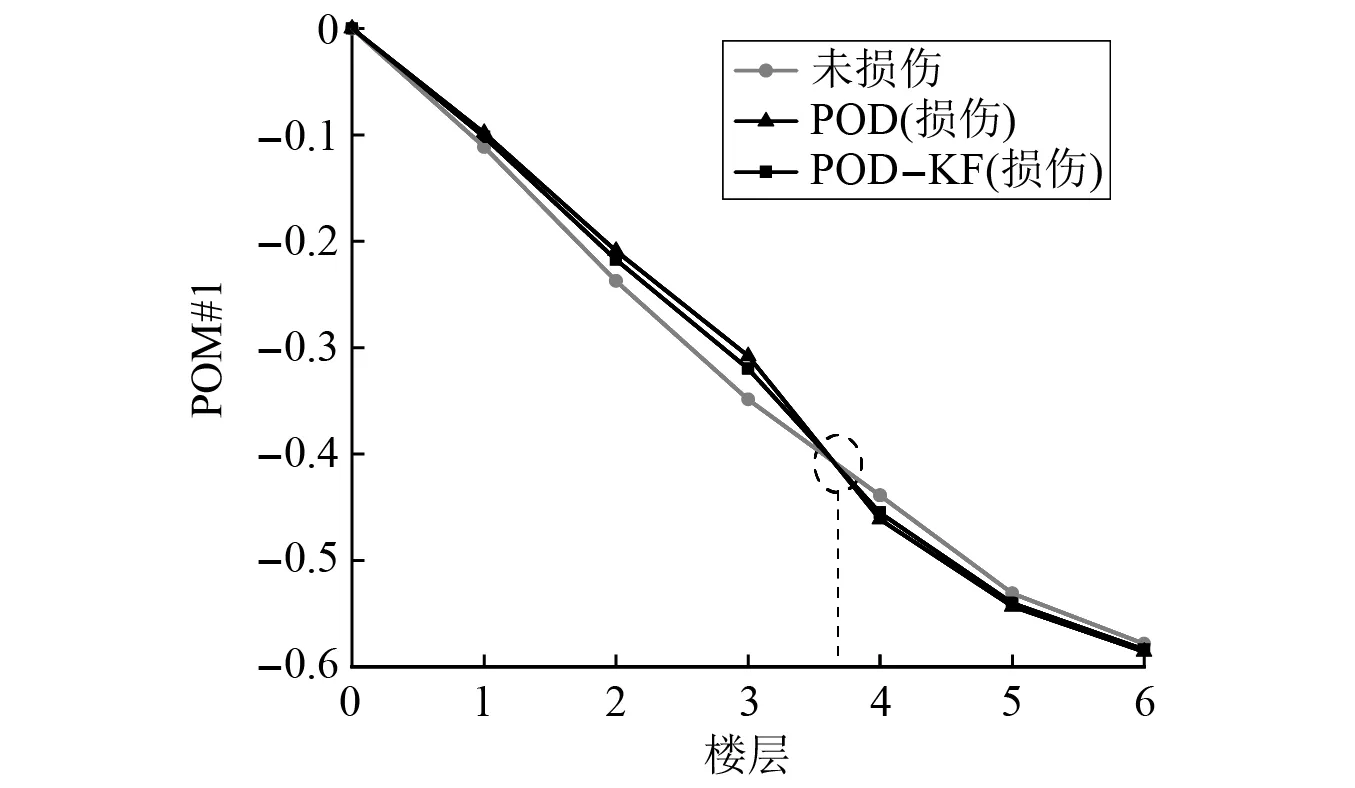
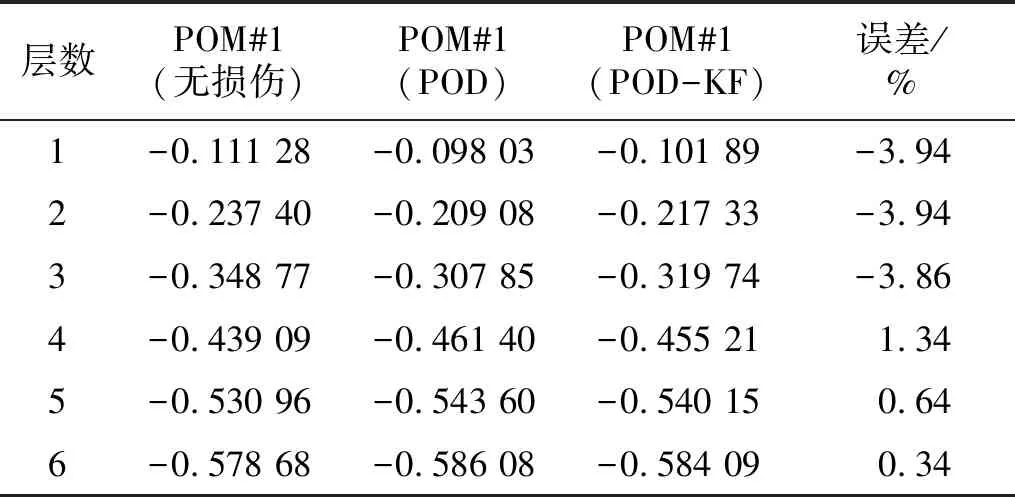
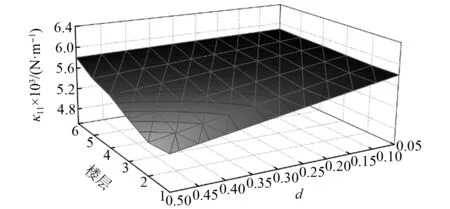
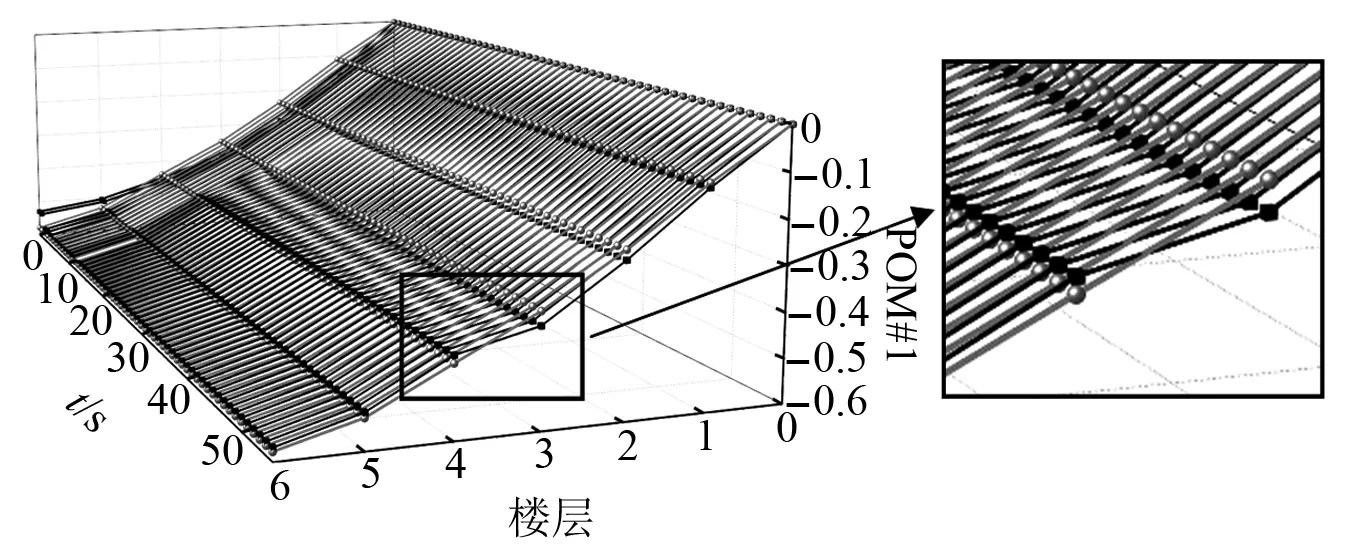
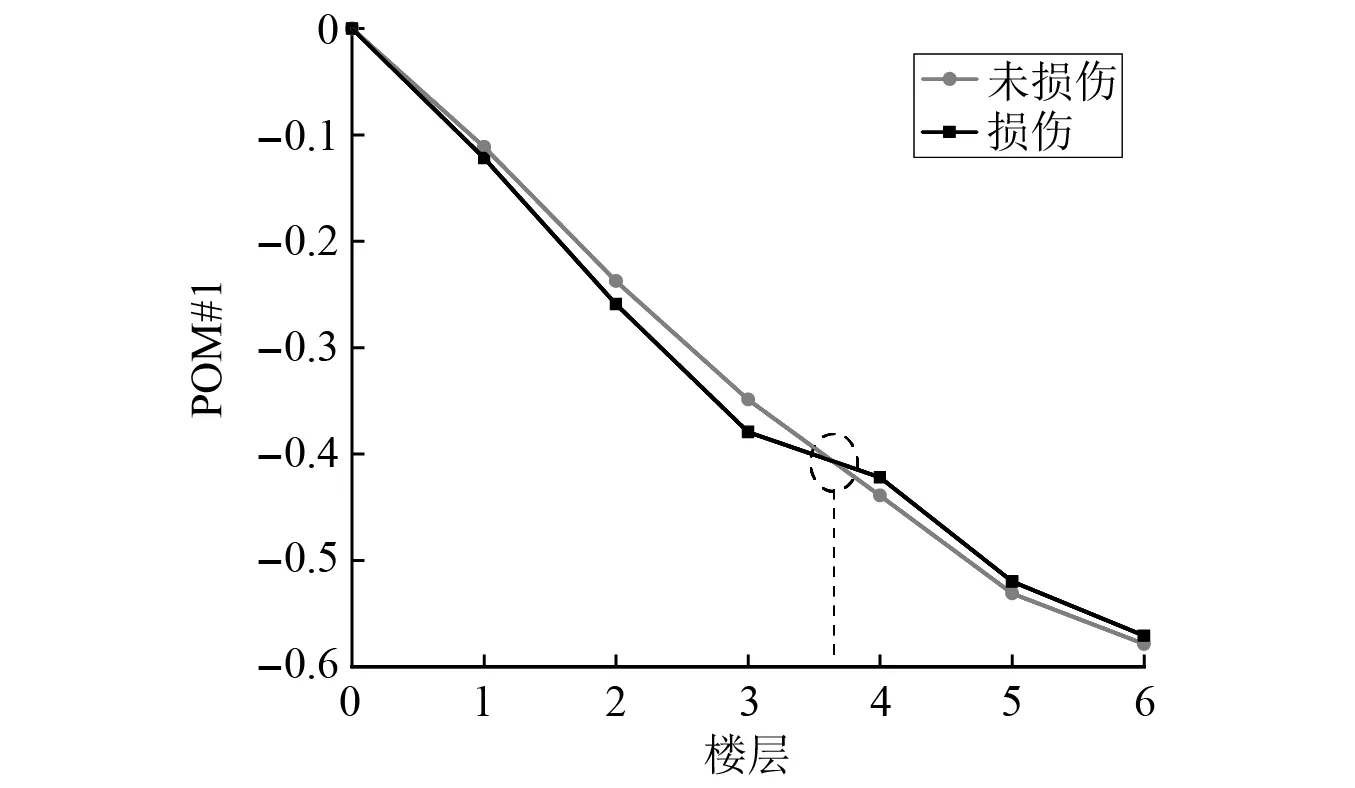
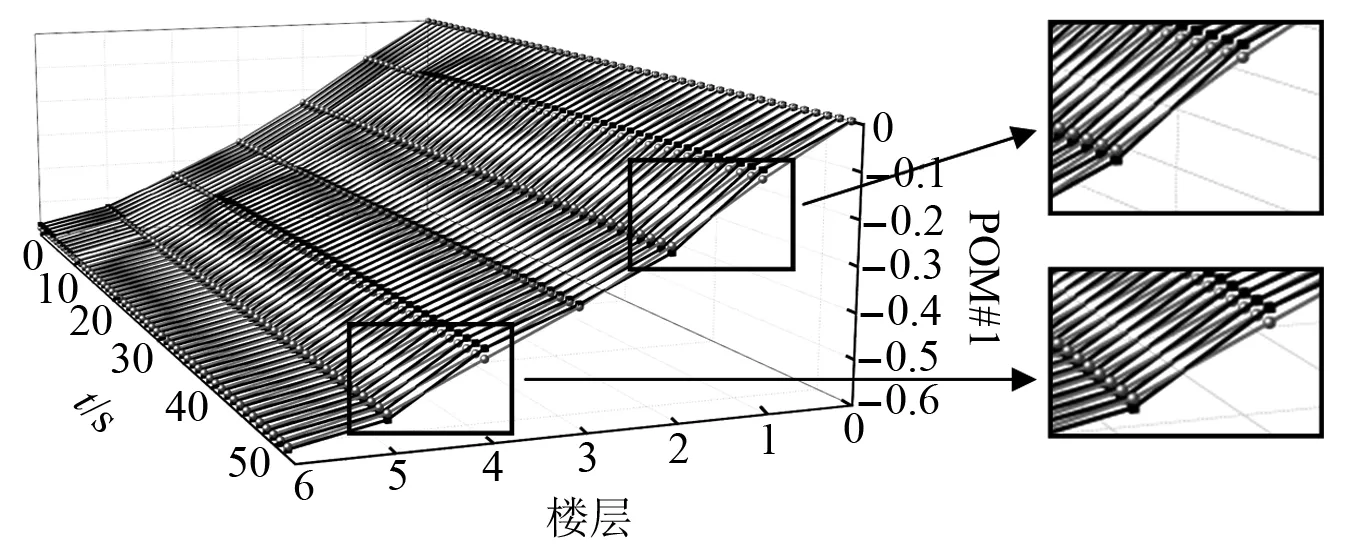
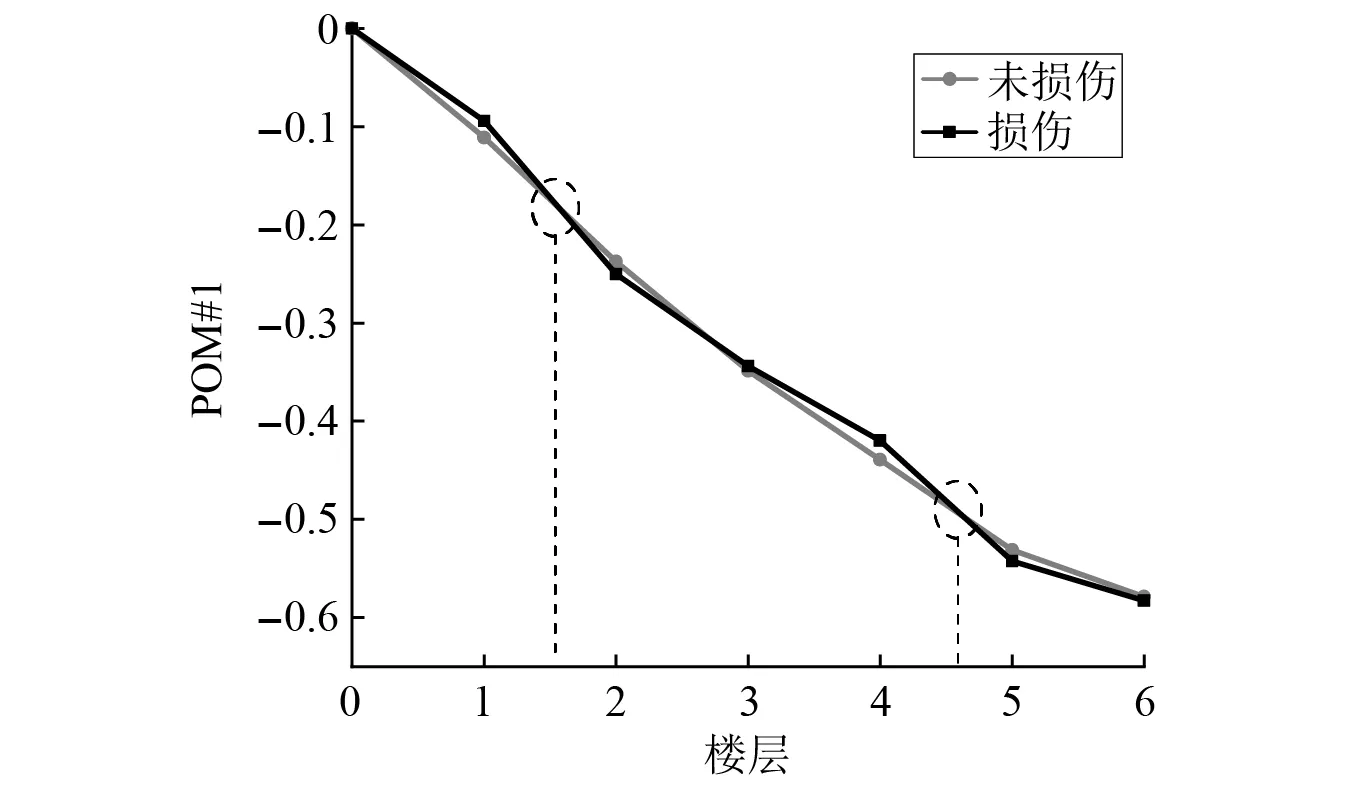
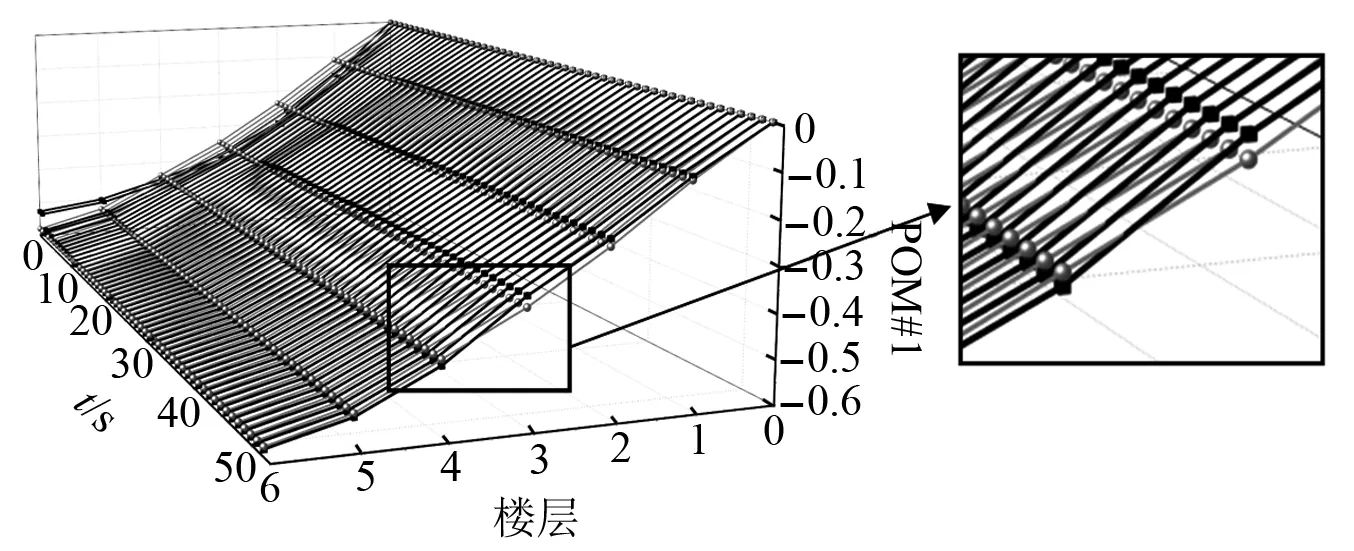
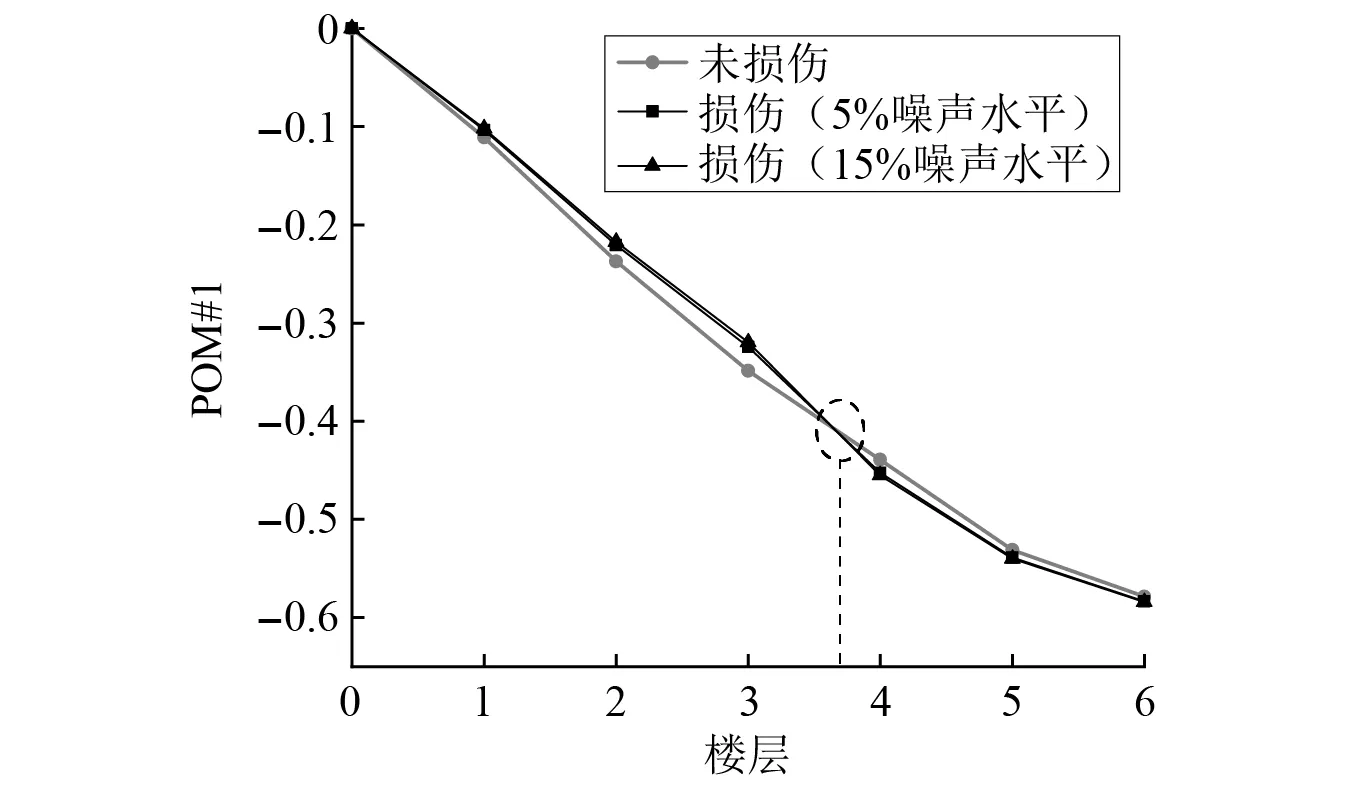
式中:考虑l 首先,需要为向量X提供一个子空间,计算n个时刻的位移u(k)=u(tk)(k=1,…,n),并将其收集到快照矩阵U中 U=[u(1)u(2)…u(n)] (5) 对快照矩阵U进行奇异值分解,可以得到 U=L·S·RT (6) (7) 当满足p≥99%时,即可认为前l阶POMs可以表示原始系统的大部分特征。以式(7)作为准则,选取此时的l值作为保留的特征模态阶数,将快照矩阵奇异值分解后得到的左奇异矩阵的前l阶列向量组成降阶矩阵。 在研究过程中,发现较大的奇异值所对应的特征向量具有相对较多的能量,由于本文所研究的对象为线弹性模型,而线性系统的状态可以用单个POM来表征,因此在对线弹性模型进行损伤识别分析时,仅需要选择最大奇异值Sii所对应的POM即可。求得结构在无损条件下模型的一阶POM与结构发生损伤时模型的一阶POM,并绘制图像,图像中损伤结构一阶POM发生突变的位置即为结构中损伤发生的位置,同时随着损伤程度的增大,其图像在损伤位置处的突变值也越大。 对于线性结构,通过一阶POM便可以对结构的损伤进行识别。然而基于SVD的POD方法会对损伤识别的实时性产生影响,因此本文的研究重点是开发一种用于在线实时更新结构POMs的方法,从而对结构前期的微小损伤以及不同程度的损伤进行快速识别。 KF方法是一种基于系统状态方程,通过系统输入和输出的观测数据,以最小均方误差为最佳估计准则,对系统的最优状态进行估计的算法,广泛用于结构各项参数的快速识别。 KF方法的核心思想是利用前一时刻的估计值和现在时刻的测量值不断对状态向量进行更新,来获取状态向量的最优估计值。在计算时首先定义系统方程式(8)和观测方程式(9) xk=Ak-1xk-1+Bk-1uk-1+wk-1 (8) yk=Hkxk+vk (9) (10) 式中:xk为系统在k时刻的状态向量;uk为已知的系统输入值;Ak为系统的状态转移矩阵;Bk为已知输入的位置矩阵;wk为系统噪声;yk为系统在k时刻的观测值;Hk为系统观测转移矩阵;vk为系统的观测噪声。 之后便可以根据上述系统方程和观测方程得到5个KF方法的基本方程。首先是状态预测过程,即根据第k时刻状态对k+1时刻的状态进行预测 (11) (12) 接下来进入更新阶段,定义实际的测量值与通过观测方程得到的估计值之间的误差为 (13) 定义此刻测量值与预测值之间误差的协方差矩阵,并写出更新矫正后的状态估计方程 (14) (15) 式中,R为观测噪声的协方差矩阵。则后验误差协方差矩阵可以表示为 (16) 式中,卡尔曼增益Kk作为最优加权值,其作用是使后验误差协方差矩阵取值最小,通过计算可以表示为 (17) 通过将以上公式循环迭代求解,就可以通过给定的初值x0和初始误差协方差P0,根据已知的观测值进行递推,对系统的状态进行最优估计。 本文考虑利用KF方法对基于POD的损伤识别方法进行改进,当出现损伤时,直接利用KF方法对所保留的投影子空间(即保留的POMs)进行在线更新,以达到实时定位损伤的目的。 为了考虑降阶模型子空间随时间的变化,将式(4)所保留的POMs以向量的形式排列如下 (18) 式中,Πl,k表示的POMs可以随时间改变,考虑到因损伤导致的系统演化,子空间随时间的演化可以表示为 (19) 与传统KF方法一样,式(19)需要用一个观测方程来补充,并根据测量值对子空间进行更新,设置测量值 (20) 首先进入预测阶段 (21) (22) 对卡尔曼增益进行计算 (23) 对子空间进行更新并对其滤波误差协方差矩阵进行求解 (24) (25) 通过对上述公式进行迭代求解,便可以实时对结构的POMs进行在线更新,以达到识别损伤的目的。 本章首先对POM的损伤敏感性进行分析,考虑了一个受地震加速度激励的六层剪切型框架,如图1所示。各层质量为:m1~m6=400 kg;层间刚度分别为:k1=120 kN/m,k2=k3=k4=100 kN/m,k5=k6=70 kN/m;层间阻尼分别为:c1=6 kNs/m,c2=c3=c4=5 kNs/m,c5=c6=3.5 kNs/m。地震动选择EL-Centro波,作用于框架底部,峰值加速度为PGA=0.5g,采样时间间隔为0.02 s,所收集位移响应的总时间为55 s。 图1 六层剪切型框架计算模型Fig.1 Calculation model of six-story shear frame 首先对该结构的动响应进行求解,利用Newmark-β法计算框架结构在地震作用下的位移和速度响应,并选取其位移响应作为观测值,同时为了更贴近实际情况,在位移响应中加入了5%的高斯噪声。之后对该剪切型框架进行POD分析:利用获取的位移响应构造快照矩阵,对其进行奇异值分解得到结构的POMs,如图2所示,从图2可以看出POMs所包含的能量随着阶数的增大而急剧减小,同时从表1的结果中发现,一阶POM的能量占比已经达到了99%,可以用于表示结构的主要特征并保证降阶模型有足够的精度。将全阶模型的结构响应与一阶POM构成的降阶模型的结构响应进行对比,如图3和图4所示,可以看出降阶模型和全阶模型的速度、位移响应大致吻合,再次证明了一阶POM可以揭示出该系统最本质的特征。 表1 未损伤结构和损伤结构本征值及能量占比 图2 未损伤结构和损伤结构的本征值(POVs)Fig.2 POVs of undamaged and damaged structures 图3 全阶模型与降阶模型三层、四层间位移响应Fig.3 Displacement response at the inter-story between the third and fourth floors of the full-order model and the reduced-order model 图4 全阶模型与降阶模型三层、四层间速度响应Fig.4 Velocity response at the inter-story between the third and fourth floors of the full-order model and the reduced-order model 图5 位于第三层和第四层间不同程度损伤结构的一阶POMFig.5 The first-order POM of structures with different degrees of damage located at the inter-story between the third and fourth floors 同样,将损伤施加到其余楼层位置,以验证该方法对不同位置损伤进行识别的可行性。图6为1~6层分别发生50%损伤的一阶POM图,从图6可以看出:对于不同的损伤位置,一阶POM对损伤均有着较高的敏感性;当损伤程度相同的情况下,框架底部及其相邻层发生损伤时其识别效果最明显,这是由于其距载荷施加的位置较近,其他楼层识别效果虽然相对较弱,但同样可以对损伤进行识别。 图6 d=50%,未损伤结构与不同位置损伤结构的一阶POMFig.6 d=50%,the first-order POM for the undamaged structure, and for the damaged located at a varying inter-story level 综上所述,对于剪切型框架结构,传统POD方法得到的一阶POM在处理损伤问题时有着较高的敏感性,而本研究的目的是开发一种能够实时跟踪损伤演化的方法,接下来将利用POD-KF方法对数值模型进行损伤识别分析,验证其有效性。 本章利用所提出的POD-KF方法对结构损伤进行识别,将加入高斯噪声的位移响应作为KF方法的观测值进行识别。在进行滤波前,需要对算法的协方差矩阵进行设置:初始协方差矩阵Ξ0=1×10-12I;系统噪声协方差矩阵WΠ=1×10-10I;观测噪声协方差矩阵Vy=1×10-10I。上述参数被称作卡尔曼滤波调节参数,通常需要在进行滤波之前进行设置与调整,这些参数应不断调整到最优值,以允许在滤波的同时对变化的参数做出快速反应[22]。本文所提出的方法能够利用结构响应对结构的时变参数进行追踪,因此调试的根本宗旨是能尽量利用测量方程,也就是使卡尔曼增益在迭代过程中始终保持较大值。 模型选用第3章的剪切型框架模型,而损伤的设置与上章有所不同,本文所分析的是时变损伤(即在分析的某一时刻出现一定程度的损伤),首先考虑单损伤工况,损伤出现时间设置在第8 s,损伤程度为50%,损伤位置位于第三层和第四层之间;利用POD-KF方法对其进分析,识别结果如图7所示。 图7 d=50%,POD-KF法一阶POM时程图Fig.7 d=50%, the first-order POM time-history diagram of the POD-KF method 图7的结果显示,当损伤出现在第8 s时,结构的一阶POM图像开始发生变化,但是在第10 s左右便可以很快收敛到稳定值,并且在损伤位置处发生突变。为了更加直观地看到损伤识别结果,图8对比了POD-KF方法得到的损伤与未损伤结构的一阶POM时程变化,灰色的球型线表示未损伤结构,而黑色的方形线表示损伤结构,可以看出当损伤发生时,方形线的时程图像会在损伤位置出现明显的突变。 图8 d=50%,POD-KF方法损伤与未损伤结构一阶POMFig.8 d=50%, the first-order POM of damaged and undamaged structures by POD-KF method 正如第2章提出的方法,这里对损伤结构的POMs的求解,并不需要像传统POD方法一样,需要对损伤结构模型进行重新训练获得,而是利用KF方法不断进行更新,以更好地与实际测量的结构响应相匹配,大大缩短计算时间。由于当损伤出现时,没有经过重新训练,因此子空间更新的最终结果会与传统POD方法有一定的差异,如图9所示。 图9 d=50%,POD-KF方法一阶POM与POD方法对比Fig.9 d=50%, comparison of the first-order POM of POD-KF method and POD method 图9将传统POD方法得到的结果与通过KF方法更新后达到稳定的POM进行了对比,并在表2中列出了两者间的误差,误差较小,说明利用KF方法更新的POM具有较高的精度。同时为了验证该方法对不同损伤程度与不同损伤位置的可行性,对利用一阶POM构成的降阶模型进行分析,考虑降阶刚度κ11的变化,从图10的结果中我们可以看出,当损伤位置从1层变到6层,损伤程度从0.05%增加到50%时,降阶刚度κ11呈现线性的变化,这为KF方法的应用提供了前提。 表2 POD-KF方法与传统POD方法对比 图10 降阶刚度矩阵对不同位置和损伤程度的变化Fig.10 Variation of reduced order stiffness matrix on different positions and damage degrees 而对于大型结构,大损伤对系统参数会产生较为明显的影响,小损伤则影响较小,再加上噪声的存在,导致目前大多数损伤识别方法无法对小损伤进行识别。然而如果不对小损伤加以重视,其会在极短的时间内发展为大损伤,在人们还未察觉的情况下对整个结构进行破坏,因此探究本文提出的方法对小损伤的敏感性,无论是在理论和实际工程中,都是一个值得研究的内容。 仍采用第3章提出的框架模型,设置损伤位于第三层和第四层之间,损伤出现时间设置在第8 s,为了验证该方法对小程度损伤的敏感性,损伤程度为5%,利用POD-KF方法对其进行损伤识别分析,识别结果如图11所示。 图11 d=5%,POD-KF方法损伤与未损伤结构一阶POMFig.11 d=5%, the first-order POM of damaged and undamaged structures by POD-KF method 结果显示,当损伤程度较小时,本文提出的POD-KF的方法仍可以较为高效地对其进行识别,从图像中可以看出,利用KF方法进行更新后,仍然能够很快收敛到稳定值,并将达到稳定后损伤结构与未损伤结构的一阶POM进行对比,结果如图12所示,可以看出当出现小程度损伤时,一阶POM的曲线在损伤处会发生突变,具有较好的识别效果,综上所述,本文采用的POD-KF方法即使是处理较小程度的损伤时仍具有较好的识别效果,证实了该方法识别结构早期微小损伤在理论上的可能性。 图12 d=5%,损伤结构与未损伤结构的一阶POM对比Fig.12 d=5%, comparison of the first-order POM between damaged and undamaged structures 然而在实际工程中,结构损伤往往不是单独存在的,而是多个不同的损伤同时存在,这对结构的威胁更大,因此接下来将考虑多工况损伤,损伤出现时间同样设置在第8 s,损伤程度为50%,但是损伤位置设置为两位置损伤,分别在第二层和第五层。利用POD-KF方法对其进分析,识别结果如图13所示。 图13 d=50%,多损伤工况下POD-KF方法损伤与未损伤结构一阶POMFig.13 d=50%, the first-order POM of damaged and undamaged structures by POD-KF method in multi-stage damage 在图13中对比了POD-KF方法得到的损伤与未损伤结构的一阶POM时程变化,灰色的球型线表示未损伤结构,黑色的方形线表示损伤结构,当损伤出现在第8 s时,与单损伤工况结果一致,结构的一阶POM图像开始发生变化,同样在第10 s左右便可以收敛到稳定值,并且在损伤位置处发生突变。可以看出当损伤发生时,方形线的时程图像会在损伤位置出现明显的突变。图14比较了POD-KF方法得到的一阶POM终值与未损伤结构的一阶POM,与图6中的结果相比较,发现当损伤出现在某两层时,其图像是其单层损伤图像的叠加:设置第二层、第五层出现损伤,其图像可以看作是图6(b)和图6(e)的叠加。该结果表明,所发展的POD-KF方法无论是处理单损伤工况还是多损伤工况,均可以对其进行快速、准确地识别。 图14 d=50%,多损伤工况下损伤结构与未损伤结构一阶POM对比Fig.14 d=50%, comparison of the first-order POM between undamaged and damaged structures in multi-stage damage 由于实际工程中更容易受到外部环境、监测设备等诸多因素的影响,所得到的响应数据往往需要考虑不同水平的噪声,为了使该方法更好地应用于工程实际,本节在第4章单损伤工况的基础上,添加了更高水平的噪声,以验证该方法在实际工程中的适用性。 选择的工况与第4章单损伤工况相同,但是在位移响应中加入了15%的高斯噪声,利用POD-KF方法对其进行分析,识别结果如图15所示。 图15 d=50%,高水平噪声下POD-KF方法损伤与未损伤结构一阶POMFig.15 d=50%, the first-order POM of damaged and undamaged structures by POD-KF method in a high level of noise 图15对比了噪声水平增高后POD-KF方法得到的损伤与未损伤结构的一阶POM时程变化,可以看出图像前4 s的结果相比于低水平的噪声,黑色的方形线波动较大,这说明在该算法的初始阶段,噪声影响较大,但随着POD-KF方法的推进,图像逐渐收敛到稳定值,之后在第11 s左右,图像在损伤位置处发生变化,并逐渐稳定,成功识别出结构的损伤。图16表示了不同水平噪声下损伤识别结果误差,可以看出虽然有一定的差异,但是基本重合,仍然满足损伤识别的要求。该结果说明,得益于卡尔曼滤波显著的降噪能力,POD-KF方法在处理高水平噪声时仍有着出色的识别能力,有着较强的抗噪能力,并且随着时间的推进,稳定性会持续增强,这为该方法应用到实际工程中提供了前提。 图16 d=50%,不同水平噪声下损伤结构与未损伤结构的一阶POM对比Fig.16 d=50%, comparison of the first-order POM between damaged and undamaged structures in different levels of noise 本研究充分利用POD和KF的优点,并将两者有机结合,发展了一种基于子空间更新的、数据驱动的POD-KF损伤识别方法,并以六层剪切型框架为例,通过数值试验,验证了该方法的有效性。主要得到以下结论: (1)利用KF方法对子空间进行更新,可以动态跟踪反应结构损伤演化的一阶POM,无论是单损伤工况还是多损伤工况,均可以实时、快速地对结构的损伤进行识别,而不需要高精度的模型,结果表明该方法可以在保持较高精度的前提下,大大减少计算量,并可以有效地抑制噪声,即使在处理结构早期小程度的损伤时,仍具有较高的精度。 (2)KF方法在识别结构参数时需要同时对外载荷进行识别,具有很大的局限性;而本文所采用的POD-KF方法,仅利用不断获取的位移响应数据便可对结构的一阶POM进行更新,无需对外载荷进行求解,使其能够对受复杂载荷影响的结构进行快速识别,具有一定的创新性。 综上所述,利用POD-KF方法对结构的一阶POM进行更新具有实时识别损伤的能力,该方法可为基于响应数据驱动的动力学降阶以及结构损伤识别领域提供新的理论和技术支撑。在接下来的研究中,将考虑更复杂的模型,并针对实际工程中的问题进行分析,在满足损伤识别精度的同时,对传感器的数量以及位置进行优化。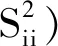
2 基于POD-KF的结构损伤识别方法
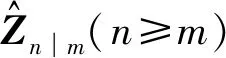
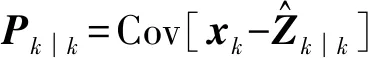
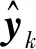
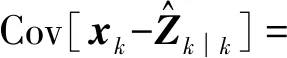
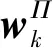
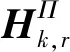
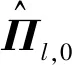
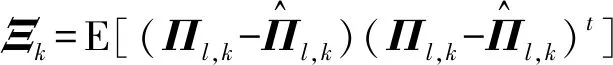
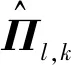
3 一阶POM的损伤敏感性分析
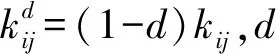
4 POD-KF方法的数值验证
5 抗噪性分析
6 结 论

