高陡山区大跨度钢箱梁悬索桥风致振动试验和气动外形优化
陈应高, 康 佳, 唐浩俊,3, 郑凯锋, 李永乐,3
(1.西南交通大学 土木工程学院,成都 610031; 2. 贵州省交通规划勘察设计研究院股份有限公司,贵阳 550081;3. 风工程四川省重点实验室,成都 610031)
在我国的西南山区,横断山脉与云贵高原受澜沧江、金沙江以及怒江等的切割,峡谷沟壑遍地,地形表现出极大的落差。山区峡谷阵风强烈,风切频繁,桥址区的风速场在空间分布复杂[1],受河谷走向急变及高陡山体的遮挡,来流风与水平面往往存在较大的夹角。当大跨度桥梁跨越高陡峡谷时,易受到大攻角强风的不利影响,对结构的抗风安全提出了更高的挑战。桥梁的风致振动包括发散振动和限幅振动,也是大跨度桥梁在设计阶段就需要考虑的控制性因素之一。
颤振是一种发散振动,当来流风速超过桥梁的颤振临界风速时桥梁可能出现振幅不断增大的扭转振动或弯扭耦合振动。山区大跨度悬索桥多采用钢桁加劲梁,而大风攻角下钢桁加劲梁的颤振性能可能会出现明显下降。王云飞等[2]对大风攻角范围下的钢桁梁大跨度桥的颤振临界风速进行了测试并对比了多种气动优化措施,发现大风攻角与小风攻角颤振性能差异明显,且不同攻角对同种优化措施的敏感程度不同。Wang等[3]对山区大跨度钢桁架悬索桥进行了节段模型风洞试验,结论指出设置气动翼板和中央稳定板有助于提高主梁的颤振临界风速,且提高程度受安装的位置和高度影响。郭俊杰等[4]考虑了山区可能出现的大攻角来流,以某大跨钢桁梁悬索桥为对象,研究了不同风攻角下不同形式的稳定板对桥梁颤振性能的影响。
钢箱梁是大跨度悬索桥加劲梁的另一种形式,在其两侧安装风嘴可以使截面表现出流线体特性,有利于桥梁的颤振稳定性。随着桥梁跨度不断增大,采用分离式双箱梁或多箱梁更有利于桥梁的颤振稳定性,例如土耳其1915恰纳卡莱大桥,其主跨为2 023 m;我国的西堠门大桥,其主跨为1 650 m,都采用了分离式双箱梁。但是,随着来流风攻角的增大,流线型箱梁断面逐渐表现出钝体截面的特性,颤振性能同样将发生明显下降[5]。安伟胜[6]在研究龙江大桥颤振性能时指出,桥梁在正攻角下颤振性能较差,优化人行栏杆构造和增大透风率可以明显改善主梁断面的气动性能。
涡激共振是一种限幅振动,也是大跨度悬索桥设计中需要重点考虑的问题。来流风经过钝体主梁时易发生分离并在尾流侧产生交替脱落的漩涡。当漩涡脱落频率与桥梁的竖弯或扭转频率接近时,桥梁可能在周期性漩涡的激励下发生竖向或扭转方向的共振现象。钢桁梁由纵横交错的杆件与桥面板组成,不同构件的漩涡脱落特性不同,且彼此之间存在明显的气动干扰现象,这在一定程度上减小了钢桁梁发生涡激共振的可能性[7]。翟晓亮等[8]针对跨越高原峡谷的钢桁梁悬索桥开展了风洞试验,指出该桥设置中央稳定板前后均没有在设计风速以下发生涡激共振现象。Fang等[9]研究了某钢桁梁悬索桥的涡振性能,发现检修道等附属设施的存在可导致周期性漩涡脱落,造成桥梁发生扭转涡振。钢箱梁在大风攻角来流作用下的涡振问题较为突出。张佳[10]通过研究大跨度钢箱梁悬索桥涡振性能发现,原断面在+5°攻角发生了明显的涡激共振,通过减小栏杆基石的高度可以有效抑制涡振;张建等[11]研究了导流板对扁平钢箱梁断面涡振性能的影响,结果表明紧贴风嘴的宽导流板能有效地抑制加劲梁涡振;朱思宇等[12]针对流线型扁平钢箱梁的涡振性能进行了风洞试验,指出较大的正攻角下人行道护栏会显著影响桥面上方气流漩涡的结构与位置,进而影响加劲梁的涡激振动性能。
由此可见,大跨度悬索桥结构纤柔,阻尼较小,加劲梁的自振频率较低,容易发生风致振动。安装气动措施是提高桥梁颤振稳定性和减小涡振响应的最有效方法,可有效改善山区大跨度悬索桥的气动措施包括中央稳定板、水平导流板、改变护栏透风率等。对于钢桁梁与钢箱梁在颤振优化上都有较好的应用。如设置中央稳定板是两种桥型较为常用的方案,能较明显提升颤振临界风速,考虑到上桥面行车以及美观问题,桁架中多考虑设置下中央稳定板或是不同高度的上下中央稳定板组合;导流板有水平导流板和斜导流板之分,钢箱梁多在风嘴处设置,并可考虑不同倾角[13],钢桁梁则多选择在上桥面两侧或是桁架内侧设置导流板;两种桥型都有较多考虑对护栏的透风率和高度进行优化,端部护栏多增大透风率以减小对来流的分离作用,中央护栏多封闭以在一定程度上起到中央稳定板的效果[14]。但是,由于这些气动措施的安装,加劲梁的气动外形将发生改变,故有利于加劲梁颤振性能的气动优化措施不一定有利于涡振性能,而大攻角来流对桥梁抗风性能的不利影响则更进一步激化了这一矛盾性。
山区大跨度悬索桥采用钢箱加劲梁的情况较少。为了更好地掌握高陡山区钢箱梁悬索桥的抗风性能,明确气动优化设计思路,充分考虑气动优化措施在工程中的实用性并与试验设计相结合。本文以主跨780 m的钢箱梁悬索桥作为研究对象,针对桥梁颤振性能较差的问题,从提高护栏透风率、增设中央稳定板、改进风嘴构造3个途径入手,对加劲梁的气动外形进行了优化设计,并通过风洞试验进行了验证。同时,结合桥梁的涡振响应进一步评价了气动优化设计思路的有效性,为山区大风攻角下的大跨度钢箱梁悬索桥的气动优化及其风洞试验设计提供参考。
1 结构动力特性
1.1 工程背景
绿汁江大桥主桥采用单塔单跨悬索桥设计,全桥设有2根主缆,中心间距为28 m。绿汁江桥总体布置如图1所示,主跨为780 m,主缆矢跨比为1 ∶11。桥塔全高156 m,采用C50混凝土桥塔。绿汁江大桥(见图1)地势起伏大,越岭线路长,地形狭窄。峡谷两侧山高,气流受阻,垂直方向气候差异明显,桥址区风特性复杂。
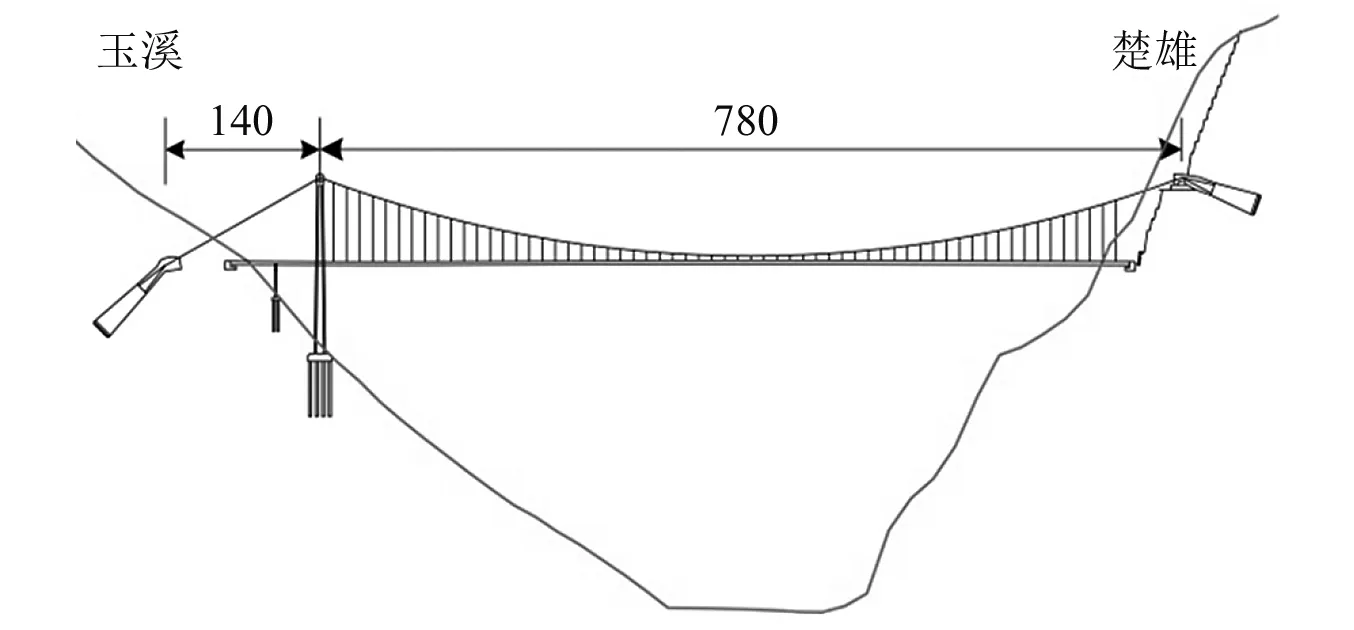
图1 主桥立面布置图(单位:m)Fig.1 Elevation of the bridge (m)
绿汁江大桥加劲梁用整体式钢箱梁设计,箱梁高3 m,宽31.4 m,左右两侧布置有外侧防撞护栏和检修道护栏,中间布置有中央防撞护栏。在原设计方案中,外侧防撞护栏高度为1.56 m。由于新的规范要求,后将两侧的防撞护栏高度增加到了1.9 m。1/2加劲梁的标准截面图如图2所示。此外,在防撞护栏的外侧还设置了检修道护栏,其下为挡水板。在桥面下侧设置了检修车轨道,其两侧为导流板。
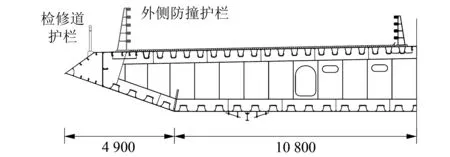
图2 绿汁江桥加劲梁标准断面(mm)Fig.2 Standard cross-section of the girder (mm)
绿汁江大桥跨越高陡山区深大峡谷,周围地势起伏剧烈。根据JTG/T 3360-01—2018《公路桥梁抗风设计规范》[15],对于一些特别地形地区,可增加均匀流场-7°和+7°风攻角下的颤振稳定性检验。另外,考虑到该桥位处平均风速随攻角增大下降明显,以及±7°时风洞试验裸桥的阻塞率已经达到5.6%,确定了绿汁江大桥颤振检验时需要考虑的风攻角α,并再结合桥址区风特性的数值模拟[16],确定了各风攻角对应的设计基准风速U0和颤振检验风速Ucr,如表1所示。

表1 桥梁的设计风参数
1.2 结构动力特性
绿汁江大桥采用单塔钢箱梁悬索桥方案,建模基于有限元分析软件ANSYS分析桥梁结构的动力特性,在有限元模型中,加劲梁和主塔用Beam4单元进行模拟,材料分别为钢材和C50混凝土。主缆采用高强钢丝,用Link8杆单元进行模拟。主缆和加劲梁之间通过平行双吊索连接,吊索采用Link8杆单元模拟,材料为钢材。施加相应约束后,有限元模型如图3所示。

图3 桥梁的有限元模型Fig.3 Finite element model of the bridge
对桥梁进行模态分析,得到结构的动力特性。桥梁的颤振临界状态通常可由竖弯和扭转基频确定,考虑了一阶对称扭弯模态组合和一阶反对称扭弯模态组合,各模态频率及振型如表2所示。将正对称扭弯模态参数和反对称扭弯模态参数分别代入计算平板颤振临界风速的理论公式。这里考虑了JTG/T 3360-01—2018《公路桥梁抗风设计规范》中所给出的Selberg公式和Van der Put公式,取它们的平均值对两种模态组合进行评价。正对称扭弯模态组合对应临界风速仅为反对称扭弯模态组合对应临界风速的0.66倍。显然,正对称扭弯模态组合更不利,即绿汁江大桥的颤振临界状态由正对称扭弯模态组合控制。
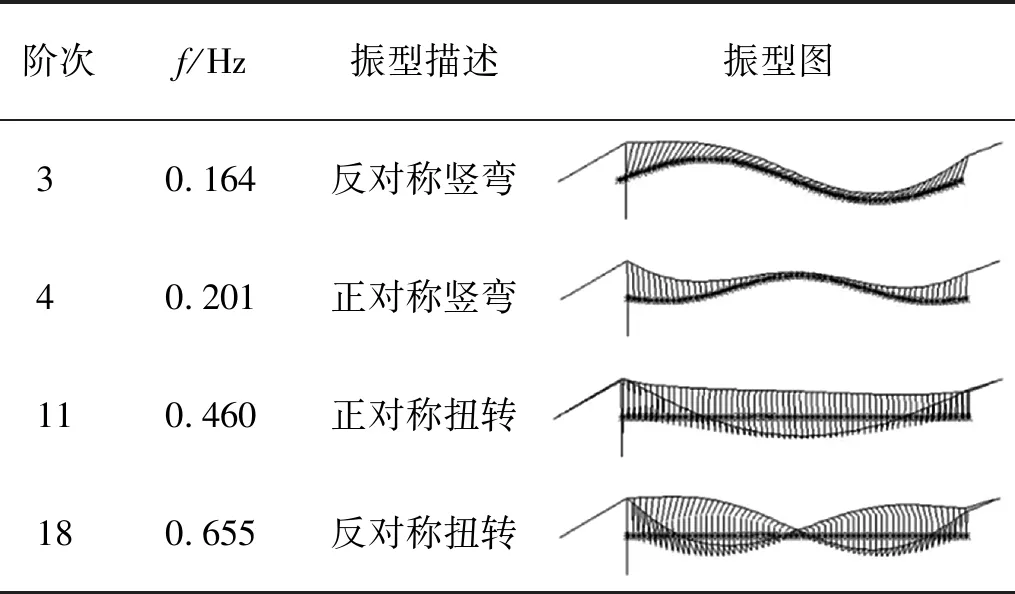
表2 桥梁的动力特性
2 桥梁颤振性能及优化对策
2.1 节段模型风洞试验参数
试验在西南交通大学XNJD-1工业风洞第二试验段中进行,直接测试均匀来流作用下模型发生颤振失稳的临界风速。试验中,来流风向不变,通过旋转模型的方式实现了0°,±3°,±5°,±7°风攻角的模拟。刚性模型由两侧各4根拉伸弹簧悬挂支撑,实现了可竖向振动和绕模型轴线转动的二自由度振动系统。模型两端设置了竖向端板,以减少端部三维绕流对模型气动特性影响,保证节段模型风洞试验的二维流场特性。安装在风洞中的动力节段模型如图4所示。在模型上游放置了眼镜蛇三维脉动风速测量仪测试来流风速大小。
采用直接测量法进行颤振试验时,要求模型系统满足动力节段模型的相似律,即要求模型与原型的弹性参数、惯性参数和阻尼参数之间保持一致。节段模型按照1/45的几何缩尺比严格模拟加劲梁的几何外形,包括附属设施。其中,护栏在满足透风率等效的基础上进行了适当的简化。根据对颤振机理的认识,该桥正对称扭弯模态组合更不利于其颤振稳定性,故根据一阶正对称扭转和竖弯的模态参数确定了试验系统的动力参数。模型系统较好地满足了如表3所示。
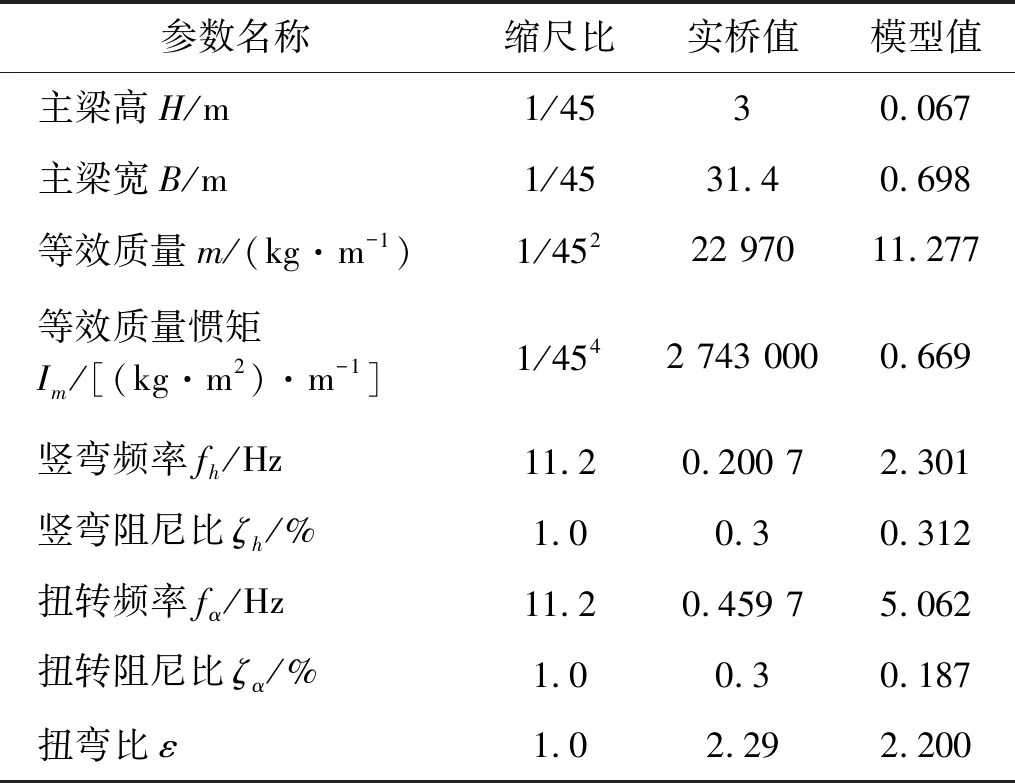
表3 试验系统的主要参数
2.2 桥梁的颤振临界风速及优化思路
首先,通过风洞试验测试了加劲梁原断面的颤振性能,7个测试攻角下桥梁的颤振临界风速如表4所示,并根据风速比将试验风速换算至了实桥风速。由试验结果可以看到,桥梁在零攻角和负攻角下的颤振性能良好,临界风速大于检验风速,但桥梁在正攻角下的颤振性能较差,临界风速小于检验风速。
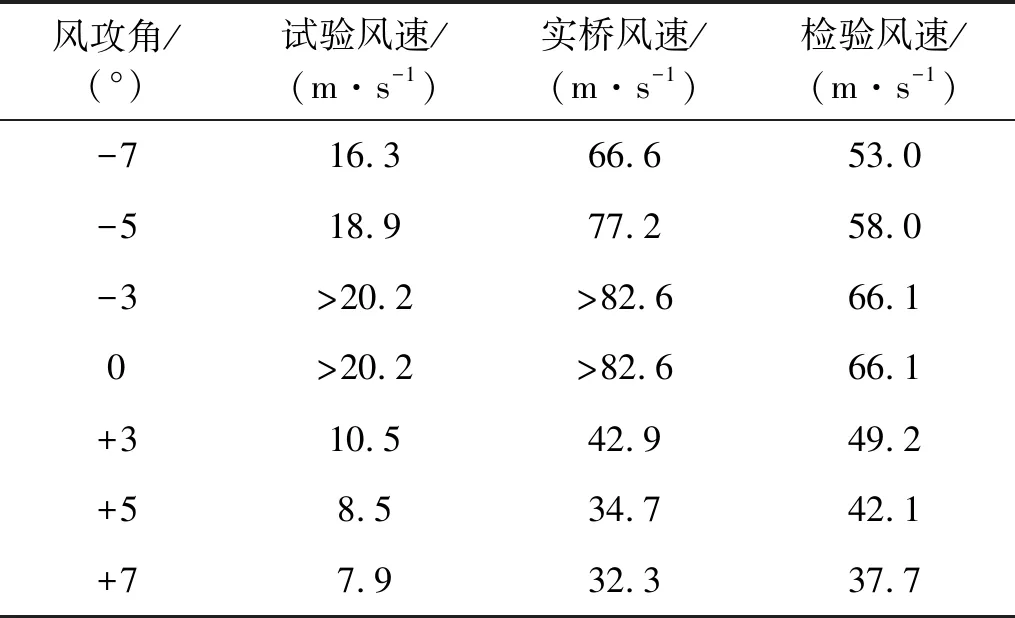
表4 桥梁的颤振临界风速
然后,对桥梁进行气动优化设计,通过有效的优化措施提高桥梁在正攻角下的颤振性能。由试验结果可以看到,桥梁的颤振临界风速随着正攻角的增大而明显减小,且表现为单自由度扭转颤振。结合前期研究成果,在大风攻角下,当来流风速高于桥梁的颤振临界风速时,来流易在迎风侧发生分离,并在端部形成大尺度漩涡,该漩涡在加劲梁扭转振动的过程中向背风侧转移,使气动力对结构做正功,成为驱动桥梁扭转颤振的主要因素。将从以下3个方面对加劲梁的气动外形进行优化:
(1)拆除端部的附属设施,以减小对来流风的阻碍。需要说明的是,实际工程中无法对附属设施进行拆除,此项比选的主要目的是确认以上对桥梁扭转颤振驱动机理的讨论。
(2)在桥面风嘴位置增设导流板,以增强对来流风的引导,减小端部漩涡的尺度及强度。
(3)在桥面中央增设竖向稳定板,阻碍迎风侧漩涡向背风侧移动,减小气动力输入的能量。
2.3 拆除端部附属设施
在箱梁两侧设置风嘴可以使来流风更平顺的经过桥面,降低流动的分离,但是该桥防撞护栏较高、透风率较小,且风嘴上还设置有检修道,其下侧为挡水板,这些附属设施的存在可能造成来流的分离,弱化了风嘴的作用,降低了桥梁的颤振稳定性。为了确定以上分析,将桥面两侧的防撞护栏和检修道护栏进行拆除,如图5所示,标记为优化方案A。
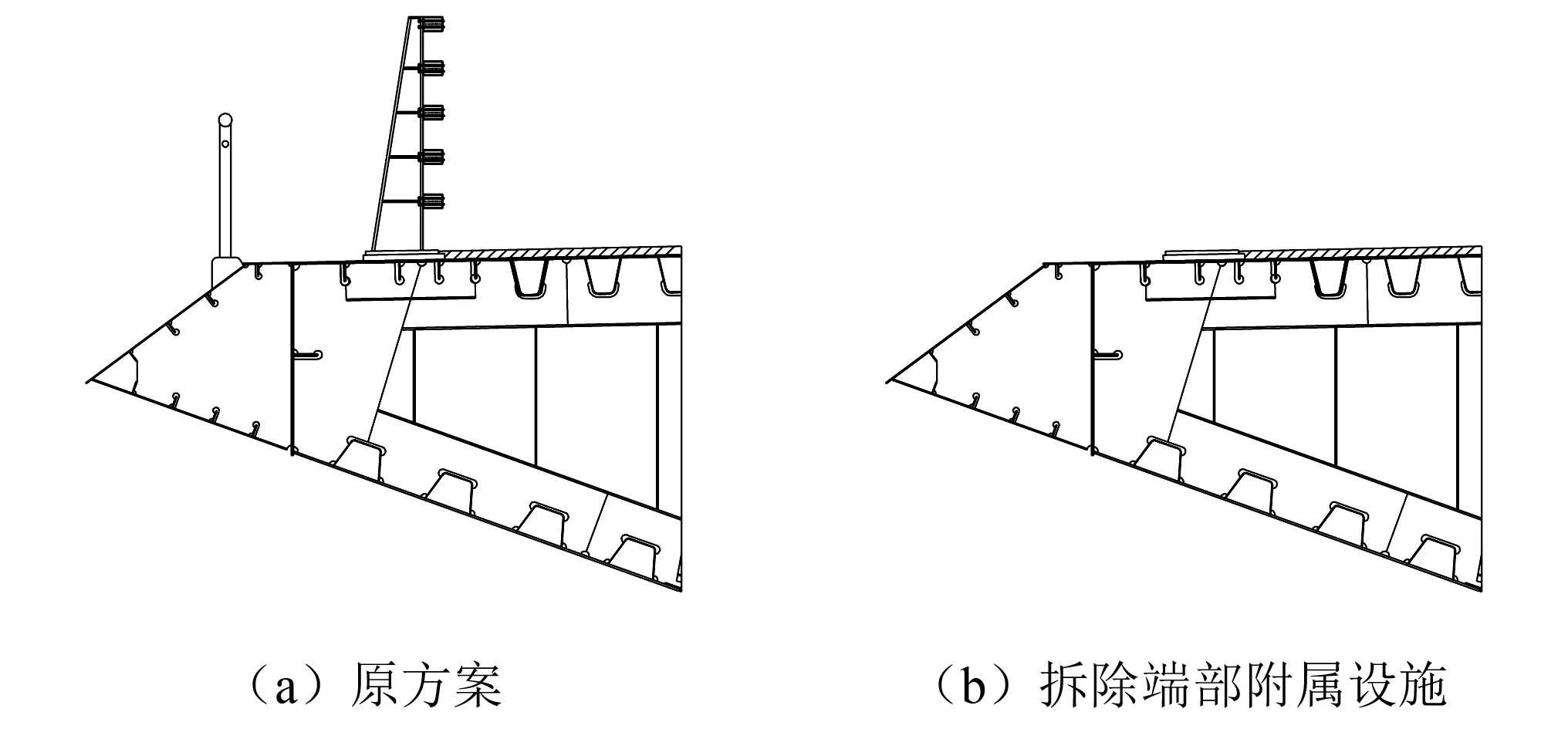
图5 优化方案A示意图Fig.5 Diagram of the optimized scheme A
该组试验工况的扭转阻尼比为0.17%、竖弯阻尼比为0.25%。通过节段模型风洞试验进行测试,采用优化方案A后,桥梁在+3°和+5°风攻角下的颤振性能得到显著提升。当实桥风速大于72 m/s时,仍未出现颤振失稳现象。这反映了关于桥梁颤振原因分析的合理性。
2.4 风嘴处增设导流板
为了降低端部附属设施的不利影响,在风嘴上侧增设了导流板,以期使来流能够更加平顺地进入桥面,减少流动的分离,提高桥梁的颤振稳定性。考虑到在工程中的应用性,与常规的横向平行设置导流板的方案有一定区别,并进一步提出了短导流板和长导流板两种方案。其中,短导流板连接挡水板边缘及风嘴中部,原风嘴的角度并未改变,标记为优化方案B1;长导流板连接挡水板边缘及风嘴边缘,相当于增大了原风嘴的角度,标记为优化方案B2,如图6所示。
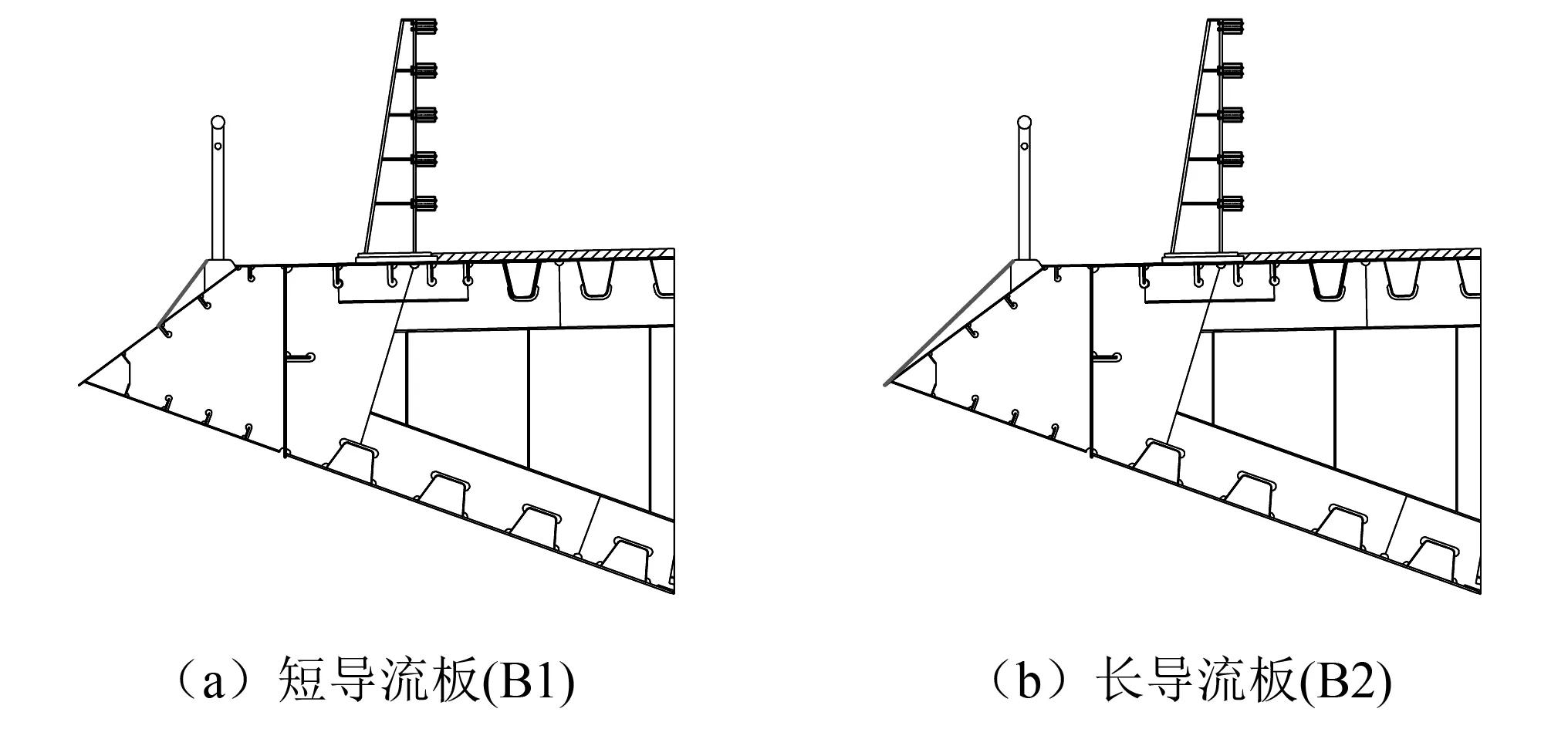
图6 优化方案B示意图Fig.6 Diagram of the optimized scheme B
该组试验工况的扭转阻尼比为0.28%、竖弯阻尼比为0.29%,试验结果如表5所示。结果表明,两种优化方式均有效,正攻角下桥梁的颤振临界风速明显提升,各攻角下桥梁的颤振临界风速均满足检验风速的要求。其中,短导流板的设置没有改变原先的风嘴角度,对桥梁的颤振性能更为有利。
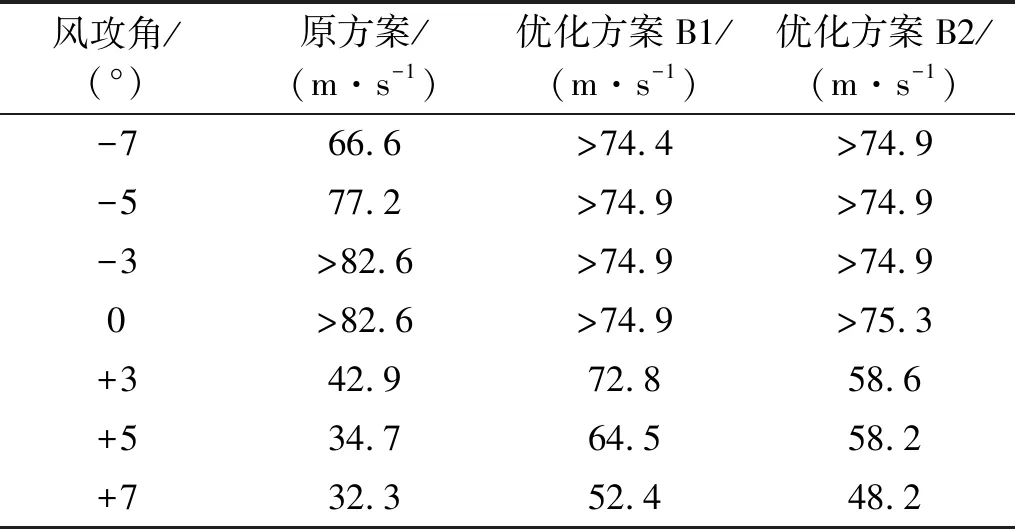
表5 设置导流板后桥梁的颤振临界风速
2.5 桥面中央增设竖向稳定板
除了通过设置导流板以削弱端部漩涡的生成外,还通过在桥面中央设置竖向稳定板以阻碍漩涡的移动。竖向稳定板的有效性已得到许多研究的验证,在实际工程中也得到了较为普遍地应用。在一定的高度范围内,随着中央稳定板的高度增加,颤振优化效果也更好[17-19]。在本研究中,通过封闭内侧防撞护栏以代替竖向稳定板,并考虑了两种高度的稳定板。其中,矮稳定板高度与内侧防撞护栏高度一致,标记为优化方案C1;高稳定板高度与外侧防撞护栏高度一致,约为内侧防撞护栏高度的1.4倍,标记为优化方案C2,如图7所示。
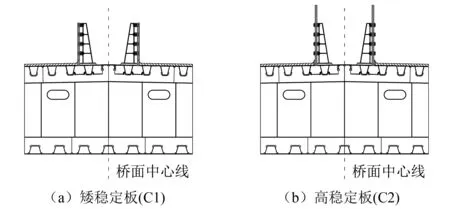
图7 优化方案C示意图Fig.7 Diagram of the optimized scheme C
该组试验工况的扭转阻尼比为0.19%,竖弯阻尼比为0.31%,试验结果如表6所示。当设置矮稳定板后,桥梁在+3°风攻角下的颤振临界风速得到了明显提升,但在+5°风攻角下的颤振临界风速仅有小幅提升,其原因是端部漩涡的尺寸会随着攻角的增大而增大,稳定板高度较低无法对漩涡的移动形成有效阻碍。增加稳定板高度后,桥梁在+5°风攻角下的颤振临界风速也得到明显提升,但在+7°风攻角下的颤振临界风速仅有小幅提升。桥址区出现较大的正攻角的可能性要小,对应的颤振检验风速也较低.虽然+7°风攻角下桥梁的颤振临界风速较低,但仍然满足颤振检验风速的要求。此外,设置高稳定板后,桥梁在零攻角和负攻角下的颤振临界风速没有出现明显下降,均大于颤振检验风速。
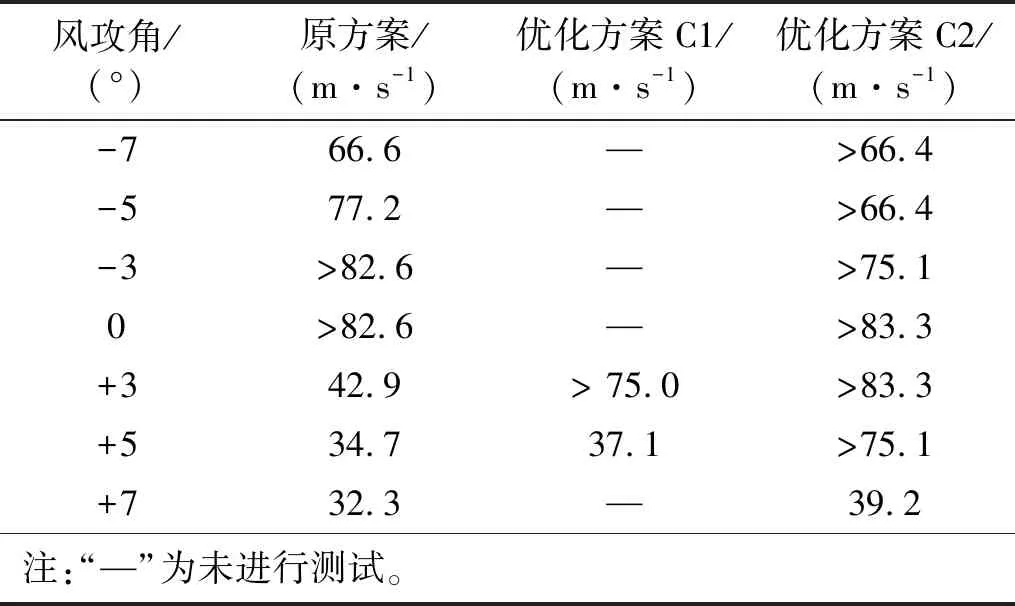
表6 设置稳定板后桥梁的颤振临界风速
3 桥梁涡振性能
第2章对桥梁的颤振性能进行了测试和优化,发现在风嘴处增设导流板或在桥面中央增设稳定板都能够有效提升桥梁的颤振性能,满足颤振检验风速的要求。除了颤振稳定性以外,桥梁在常遇风速下可能出现的涡激共振也同样需要关注。涡激共振是大跨度桥梁容易在低风速下出现的一种风致限幅振动。流线型箱梁在大风攻角作用下会逐渐表现出钝体的特征,存在发生涡激共振的可能性[20-21]。因此,本章将比较设置这两种气动措施后,桥梁的涡振性能,并据此对两种措施的有效性做进一步评价。
通过节段模型风洞试验测试该桥的涡振响应,试验参数与颤振试验保持一致。来流为均匀流,逐步增大风速,测试模型的振幅大小。节段模型的涡振振幅ym与实桥的涡振振幅yp按式(1)进行换算[22]
(1)
式中,进行竖弯涡振振幅换算时n为几何缩尺比,进行扭转涡振振幅换算时n为1。
首先,测试了在风嘴处设置导流板后桥梁的涡振响应,同样考虑了0°,±3°,±5°,±7°共7个风攻角。图8和图9分别给出了实桥竖向涡振振幅和扭转涡振振幅随实际风速的变化规律。由试验结果可以看到,设置短导流板(优化方案B1)或长导流板(优化方案B2)后,桥梁的涡振响应呈现相似的规律。在负攻角下,桥梁没有发生涡激共振现象;在零攻角下,桥梁发生了振幅较小的扭转涡振;但在正攻角下,桥梁在竖直和扭转方向均发生了幅度较大的涡激共振,且攻角越大振幅越大。总体来看,桥梁在+5°和+7°风攻角下的涡振响应最显著,竖向涡振存在一个锁定区间,扭转涡振存在两个相邻较近的锁定区间。各锁定区间内,最大振幅对应的风速受攻角的影响较小。
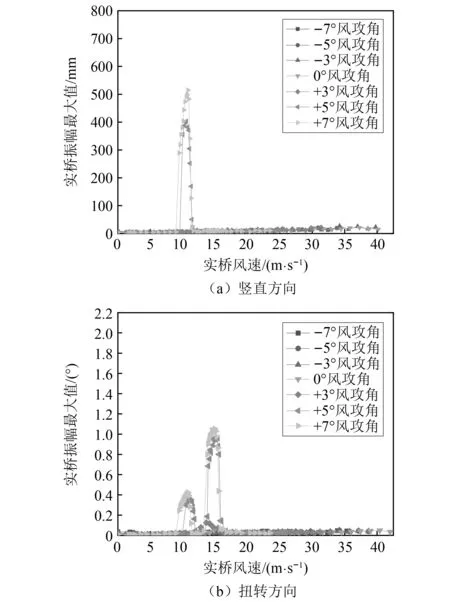
图8 采用优化方案B1后桥梁的涡振响应Fig.8 VIV response of the bridge with optimized scheme B1
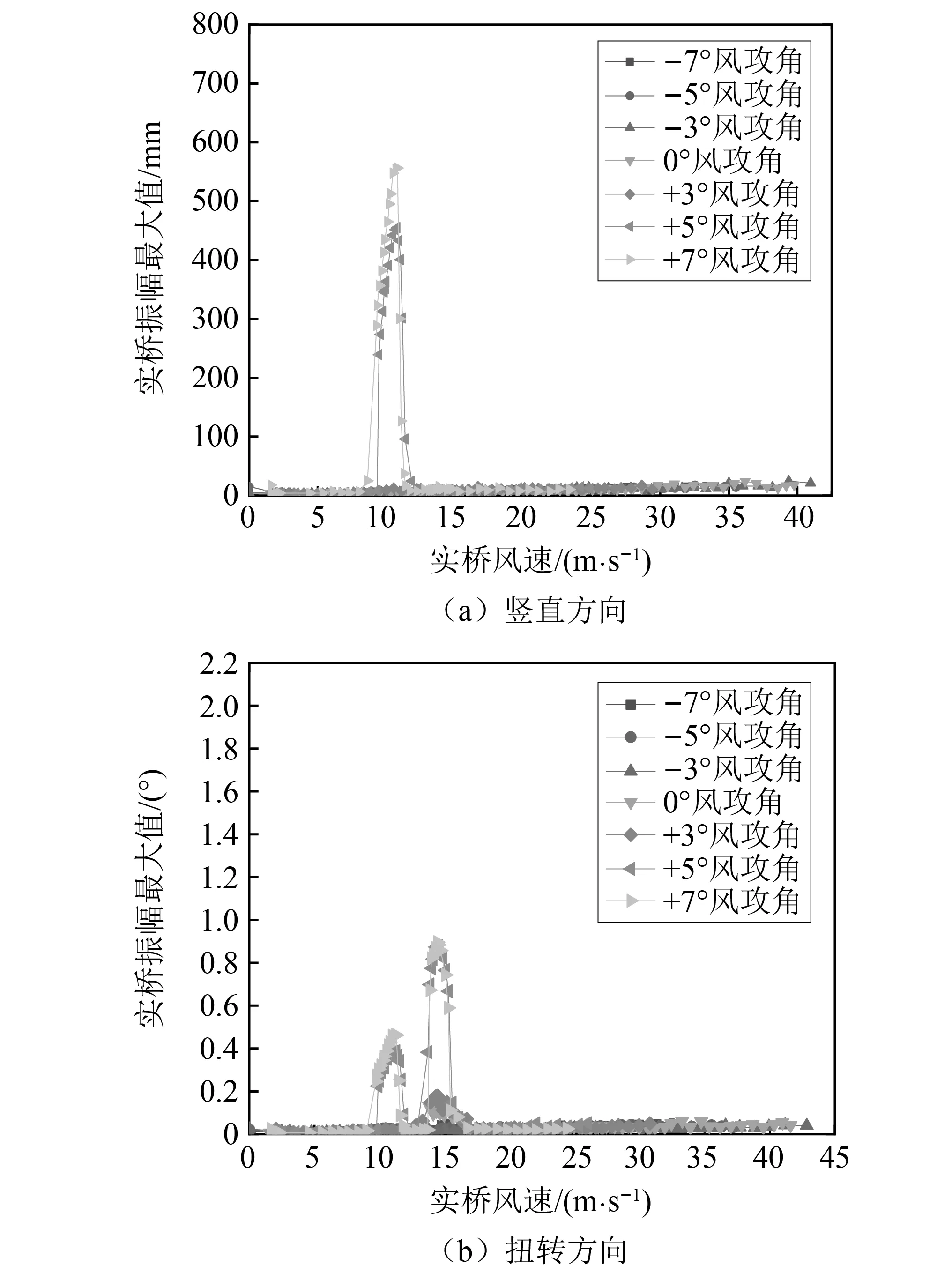
图9 采用优化方案B2后桥梁的涡振响应Fig.9 VIV response of the bridge with optimized scheme B2
然后,测试了在桥面中央增设竖向稳定板(封闭内侧防撞护栏)后桥梁的涡振响应,考虑了0°,±3°,±5°共5个风攻角。由于采用优化方案C1时桥梁在+5°风攻角下的颤振临界风速不能满足检验风速的要求,故仅测试了优化方案C2对应的涡振响应。图10给出了实桥竖向涡振振幅和扭转涡振振幅随实际风速的变化规律。与短导流板方案B1相比,安装中央稳定板后桥梁的竖向涡振振幅有所降低,+5°风攻角下最大振幅降低了35.2%,但是桥梁在-3°风攻角下也出现了较为明显的涡振。桥梁的扭转涡振振幅有所增加,+5°风攻角下最大振幅增加了37.5%,且桥梁在所有测试攻角下都出现了明显的涡振,对应的振幅和锁定风速相近。考虑到桥址区的来流出以负攻角为主,因此负攻角下桥梁存在发生涡振的可能更为不利。
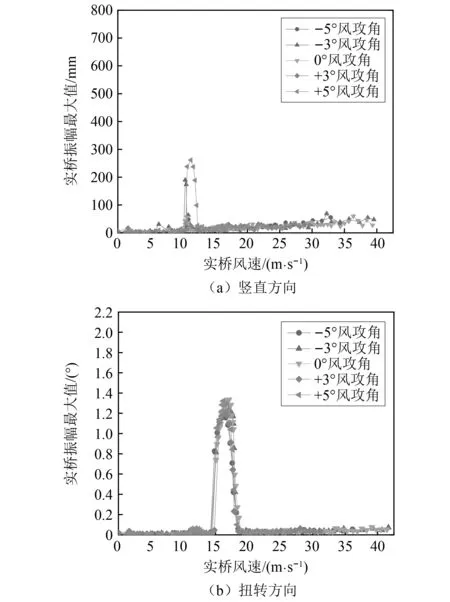
图10 采用优化方案C2后桥梁的涡振响应Fig.10 VIV response of the bridge with optimized scheme C2
JTG/T 3360-01—2018《公路桥梁抗风设计规范》指出涡激共振检验宜在均匀流场、0.25倍设计紊流强度流场、桥址设计紊流强度流场中进行,并以0.25倍设计紊流强度流场作为最终涡激共振评价依据。桥梁纵向脉动风速的设计紊流强度Iu可按式(2)计算。
(2)
式中:Z为主梁的基准高度;z0为桥址区的地表粗糙高度。
该桥桥址区位于高陡山区,周围被起伏剧烈的山体环绕,属于D类地表,故地表粗糙高度z0为1.0 m。该桥桥面距离水面的高度为318 m,对跨越深切河谷的桥梁可按照上述高度的2/3确定主梁的基本高度Z为212 m。将以上参数代入式(2)可得该桥纵向脉动风速的设计紊流强度Iu为18.7%,故0.25倍的设计紊流强度为4.7%。在西南交通大学XNJD-1风洞中,在模型前方设置格栅板以形成紊流场,然后通过调整格栅板的透风率以及格栅板到模型的距离来更改紊流强度,以满足试验需要,如图11所示。

图11 紊流场中的节段模型Fig.11 Segmental model with turbulent flow
仅针对优化方案B1进行了测试,图12给出了该桥在0.25倍设计紊流强度流场下涡激共振振幅最大值随风速的变化关系。与图8中的结果对比可以看出,在紊流场中,桥梁在7个测试风攻角下均未出现明显的涡激共振现象。各攻角下桥梁的竖向振动、扭转振动响应随着风速的增加而增加。
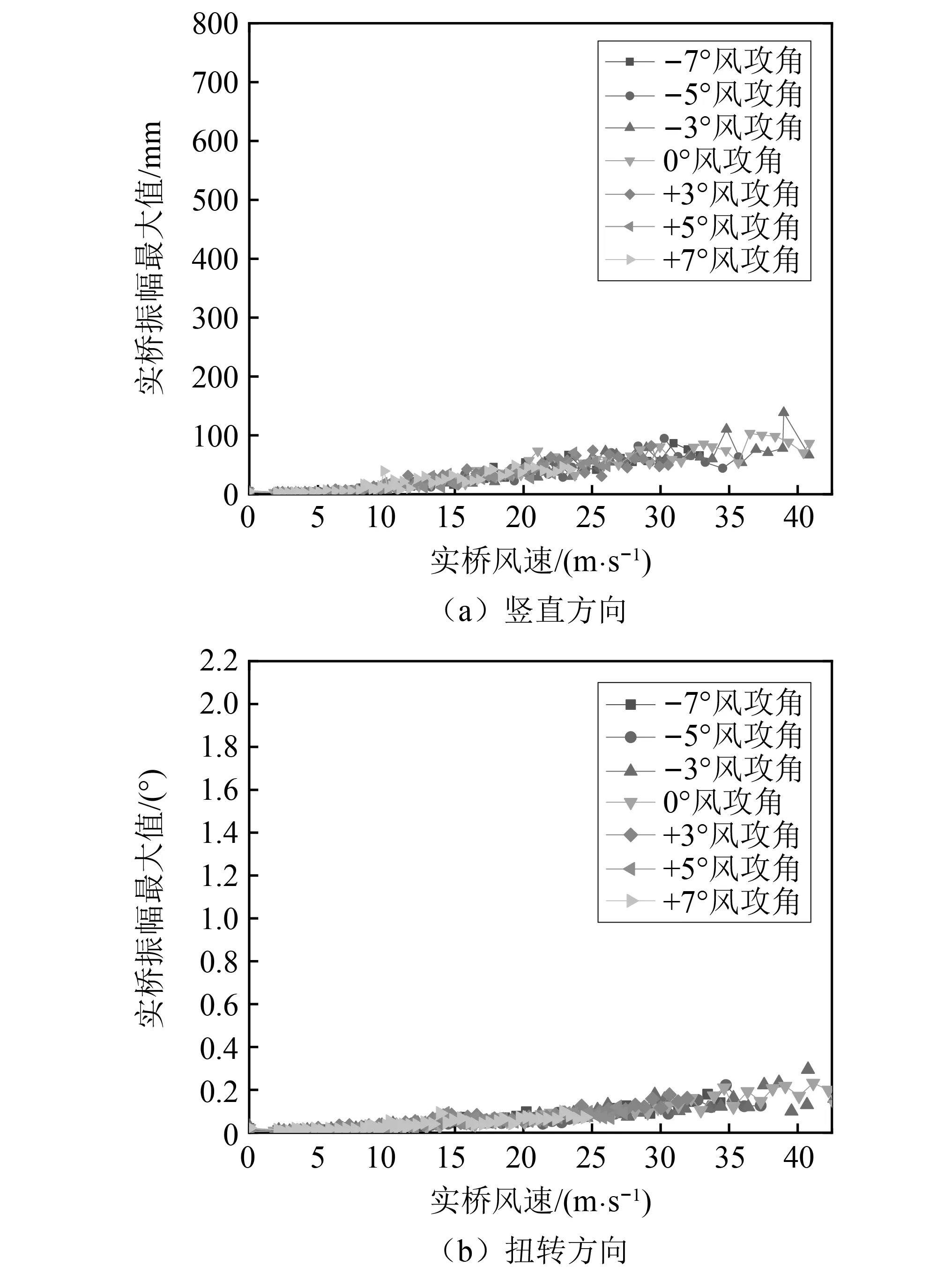
图12 紊流场中桥梁的涡振响应Fig.12 VIV response of the bridge with turbulent flow
4 结 论
本文对跨越高陡山区的大跨度钢箱梁悬索桥的抗风性能进行了试验研究,测试了不同风攻角下的颤振性能,发现较高的防撞护栏和风嘴上方的检修道不利于桥梁在正攻角来流下的颤振稳定性。因此,设计了有利于桥梁颤振稳定性的气动优化措施,并结合桥梁的涡振性能对气动优化措施的有效性进行了评价,即在满足颤振性能的基础上尽可能减小涡振的产生,得到以下主要结论:
(1)在风嘴上侧增设导流板可以有效改善桥梁的颤振稳定性。导流板的存在可以使来流风更加平顺地进入桥面,减少流动的分离,有利于削弱大攻角来流下端部漩涡的生成。该措施的有效性与其长度有关,当导流板较长而覆盖了整个风嘴时,相当于增大了原风嘴的角度,削弱了导流板的有效性。
(2)在桥面中央增设竖向稳定板也可以有效改善桥梁的颤振稳定性。随着正攻角的增大,桥面迎风侧大尺寸漩涡的形成及其向背风侧的移动将成为驱动桥梁发生扭转颤振的主要原因,故需要更高的稳定板才能有效阻碍漩涡移动,提升桥梁的颤振稳定性。
(3)导流板和稳定板的设置都可以提升桥梁的颤振性能,但在较低风速下桥梁都存在发生涡振的可能性。稳定板的设置能阻碍漩涡的移动,但并没能改善来流在迎风侧的分离,桥梁竖向涡振振幅减小,但扭转涡振振幅增大,且在各测试攻角下均出现了较大的扭转涡振;而导流板的设置可以在一定程度上改善来流的分离,抑制端部漩涡的产生,桥梁仅在较大的正攻角下才出现涡振。故两种优化措施从抑振机制上存在区别,考虑到桥址区以负攻角来流为主,故设置稳定板不利于桥梁的涡振性能。
(4)本文选择了山区较少使用的钢箱梁悬索桥,在风洞试验设计中选择了-7°~+7°的大风攻角,并考虑了颤振气动优化措施对涡振性能的影响。基于对颤振机理的认识,通过减小来流分离、阻碍漩涡移动两个方面设计了气动优化措施,在验证措施的有效性后又进一步比较了它们对桥梁涡振的影响,相关方法和结论可为后续山区钢箱梁的气动优化提供参考。但本文仍存在一些局限性,如可采用精细程度更高的大比尺模型进行试验,以提高涡振的测试精度;在措施选取上受实际工程应用性的限制,优化措施考虑较少,且试验还可以考虑更大风攻角;另外,本文侧重于试验设计,缺少对内在研究机制的分析,后续可针对优化方案进行CFD分析,明确断面附近流场情况以及漩涡的形成与移动情况,对断面颤振和涡振的产生机理进行解释。

