迎风面肋板对方柱流场和气动力的影响研究
蒋 媛, 刘锦阳, 刘 锐, 回 忆
(1. 中国电建集团成都勘测设计研究院有限公司,成都 610072;2. 重庆大学 土木工程学院,重庆 400045)
方形或矩形截面高层建筑作为工程中典型的钝体结构,其截面形状显著影响流动分离、剪切层和旋涡脱落,这些流场特征对于结构的气动荷载至关重要[1]。因此,许多学者提出了基于截面形状改进的气动外形修正技术[2-3]。
气动修正技术主要包括整体修正,如锥化、扭转和开洞[4-5]等和局部角修正,如圆角和切角[6]等,其中,局部角修正技术在建筑上应用更为广泛,因其对结构整体改变较小、施工方便等特点。大量风洞试验证明,局部角修正能降低模型上的气动力[6-7],圆角使模型的阻力和升力减小了约 40%和30%[8]。
为了解释局部角修正的流场机理,一些流动可视化技术,如油流法、烟迹法、粒子图像测速(particle image velocimetry,PIV)和数值模拟等被用来研究模型周围的流场信息[9]。研究表明,角修正能抑制前角区域的流动分离,进一步影响了剪切层和旋涡脱落特征。圆角和倒角通过改变前缘分离点的位置,使剪切层更靠近模型侧壁面,侧壁面分离泡变小,进而造成尾流区变窄,背风面尾涡拉长和斯托罗哈数增大[10]。然而,切角具有不同的流场机理,来流在切角区域形成小的局部旋涡,旋涡的外边界提供了一个光滑的虚拟表面使来流更易通过前角区域,并导致剪切层和涡脱等流场变化,从而减小气动力[11-12]。
此外,外立面附属物,如阳台、竖条、水平和竖向肋板也会局部改变高层建筑的气动外形,并降低风效应[13]。Stathopoulos等[14]发现阳台能降低建筑迎风面的局部风压。Hui等[15-16]通过大量风洞试验系统的研究了水平和竖向肋板对高层建筑风压和风荷载的影响。他们发现水平肋板能显著降低明显上的负压极值,竖向肋板能更好的减小高层建筑的整体风荷载,横风向脉动层风力的最大降低57.3%。Liu等[17]通过PIV试验探究了外伸附属物的流场机理,结果发现水平和竖向肋板都能使模型尾涡拉长,竖向肋板明显减小模型周围的脉动风速,并减小了剪切层曲率。然而,由于激光反射和模型的遮挡效应,模型近壁区的流动情况无法准确评估。因此,该研究只能定性地讨论外伸肋板对模型周围流场特征的影响。艾辉林等[18]利用大涡模拟(large eddy simulation,LES)研究了超高层建筑外立面复杂装饰条的风荷载特性。发现建筑表面装饰条的风荷载体型系数和局部脉动风压均呈现凹形分布,即拐角区域数值较大,建筑平顺区域相对较小。程旭[19]基于LES结果发现水平肋条可以影响高层建筑侧风面分离涡的形成和脱落,竖向肋条能使剪切层靠近模型侧壁面。
如前所述,大多数研究已经验证了竖向肋板能改善模型表面风压和风荷载。然而,外伸肋板的流场修正机理仍需系统地研究。因此,本文使用LES进一步阐明竖向肋板的流场机理,主要探讨了竖向肋板对前角流动分离、剪切层、涡脱等流场的影响,并解释了方柱上总气动力的变化的流场原因,最后,基于大量的模拟结果定量的研究了竖向肋板的布局优化。
1 数值方法
1.1 控制方程
本文采用三维大涡LES湍流模型。小涡通过亚网格尺度(subgrid-scale streese,SGS)模型进行模拟,大涡的则通过直接求解滤波操作后的流体控制方程。不可压缩流滤波后的N-S方程为
(1)
(2)
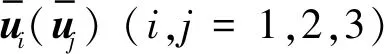
SGS亚格子应力张量τij通过涡黏模型计算得到
(3)
(4)
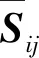
涡黏性系数νt由Smagorinsky-Lilly模型计算得到
(5)
式中:von Karman常数k=0.42;Smagorinsky常数Cs=0.1;Δ为滤波尺度。
1.2 模型信息、计算域和网格分辨率
方柱模型的尺寸为D×D×4D(方柱宽度D=50 mm),如图1所示。一般数值模拟中模型展向长度LZ取值为1≤LZ/D≤6,展向长度4D在文献中[20-21]使用最多,此长度既可以节约计算成本,也能得到准确的流场结构和风荷载,因此,本次模型的展向长度为4D。Hu等[22]发现迎风角的角修正比背风角更有效,因此,本次也在模型的迎风角附近布置两个竖向肋板(见图1)。肋板有两个布局参数,如表1所示。表1中:b为肋板到方柱边缘的距离;d为肋板的外伸长度。肋板的厚度为0.02D。
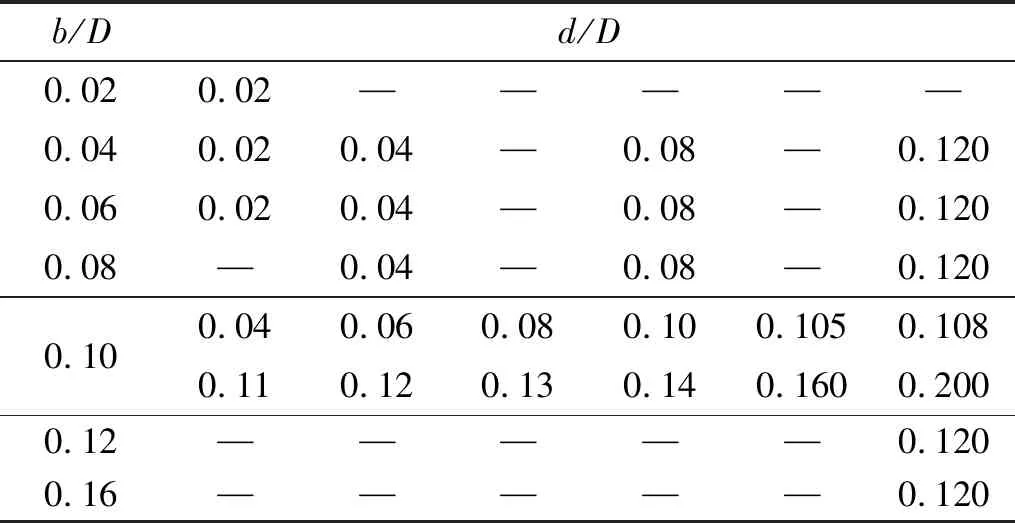
表1 计算工况
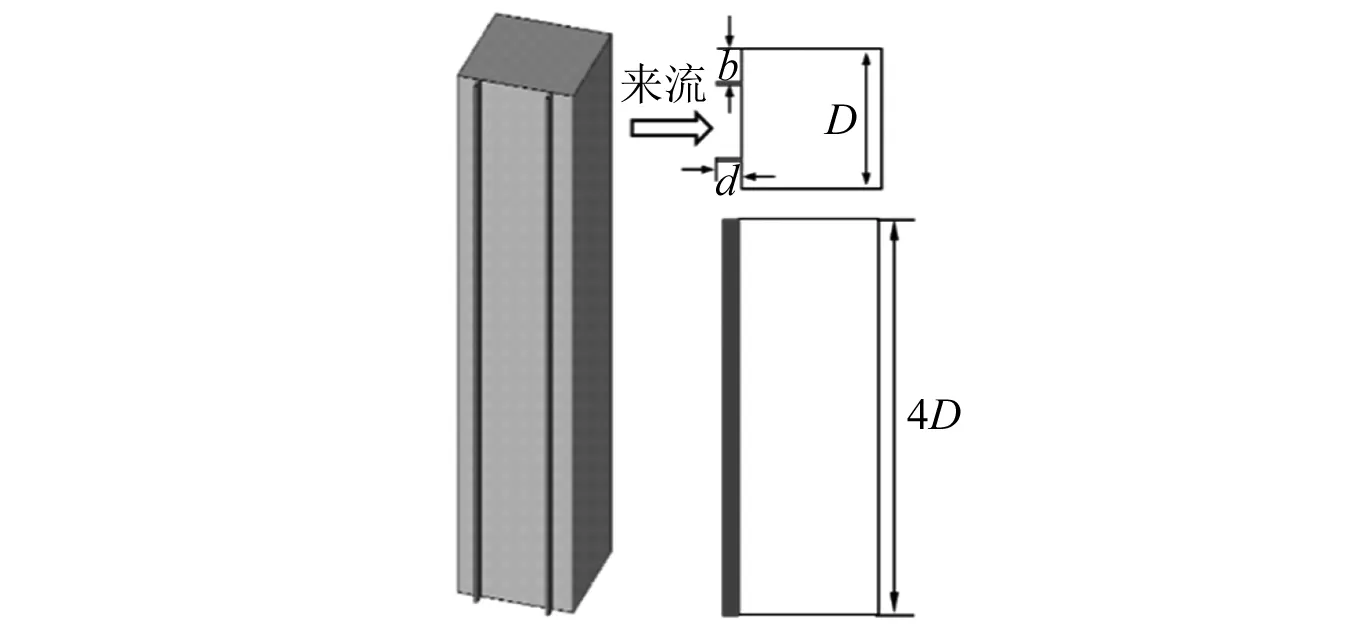
图1 计算模型Fig.1 Computational model
计算域的大小为30D×20D×4D,如图2(a)所示。方柱底面中心为坐标原点,入口到原点的距离为10D。计算域宽度为20D,对应的阻塞率为5%。
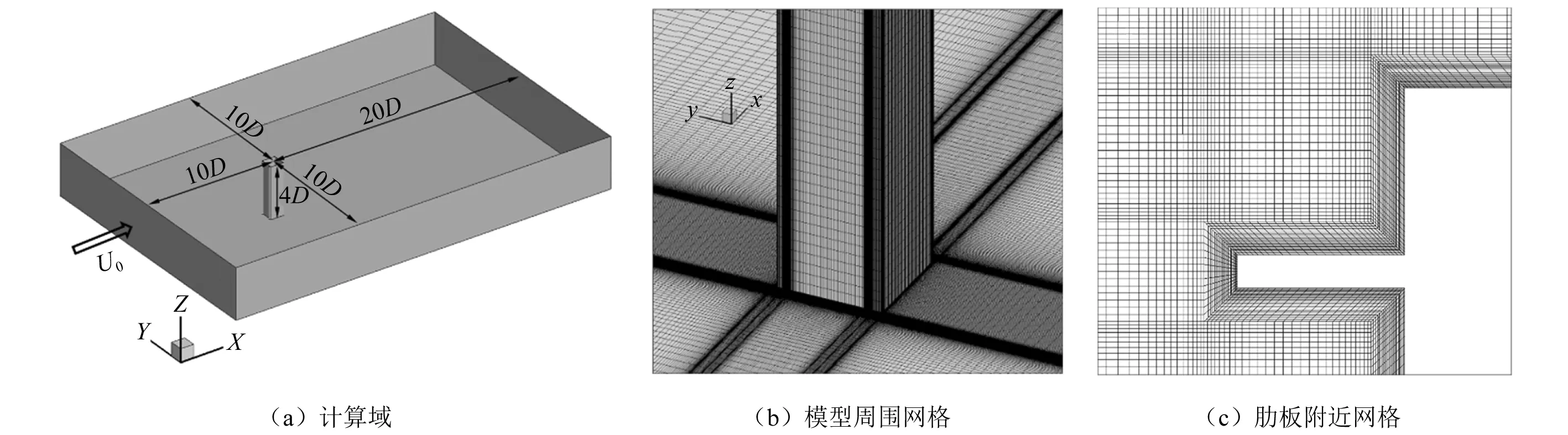
图2 计算域和网格布局Fig.2 Computational domain and mesh configuration
图2(b)和图2(c)为模型和肋板附近的网格。整个计算域内使用结构化网格。模型近壁区域的网格增长率为1.06,远离壁面区域的网格增长率为1.1,展向网格分辨率δZ/D=0.1,该分辨率满足Tamura等提出的展向网格分辨率的最低要求(δZ/D≤0.1)。本次使用3种网格方案进行网格无关性验证,如表2所示。杜晓庆等[23]检验了时间步长对模拟精度的影响,发现无量纲时间步长t*=tU0/D≤0.025时(t为模拟的时间步长),模拟结果无明显差异,本次模拟的无量纲时间步长为0.013,小于杜晓庆等建议的时间步长。
1.3 边界条件及求解策略
本研究主要考虑外伸板对流场结构的影响,因此,入口边界采用均匀来流,均匀流忽略了来流风剖面的影响,及顶部自由端效应。顺风向风速U0=6.4 m/s,其他两个方向风速为0,对应的雷诺数为Re=2.2×104。出口边界为自由流。计算域侧壁为对称边界,顶部和底部采用周期性边界。方柱表面是无滑移壁面边界条件。
数值模拟使用ANSYS Fluent软件。采用有限体积法求解不可压缩流的控制方程。压力-速度耦合选择SIMPLEC算法。动量离散采用有界中心差分格式,时间离散采用二阶隐式格式。迭代计算的收敛残差设置为1×10-5。模拟时长约为40个涡脱周期。

表2 网格信息
1.4 气动力定义和结果验证
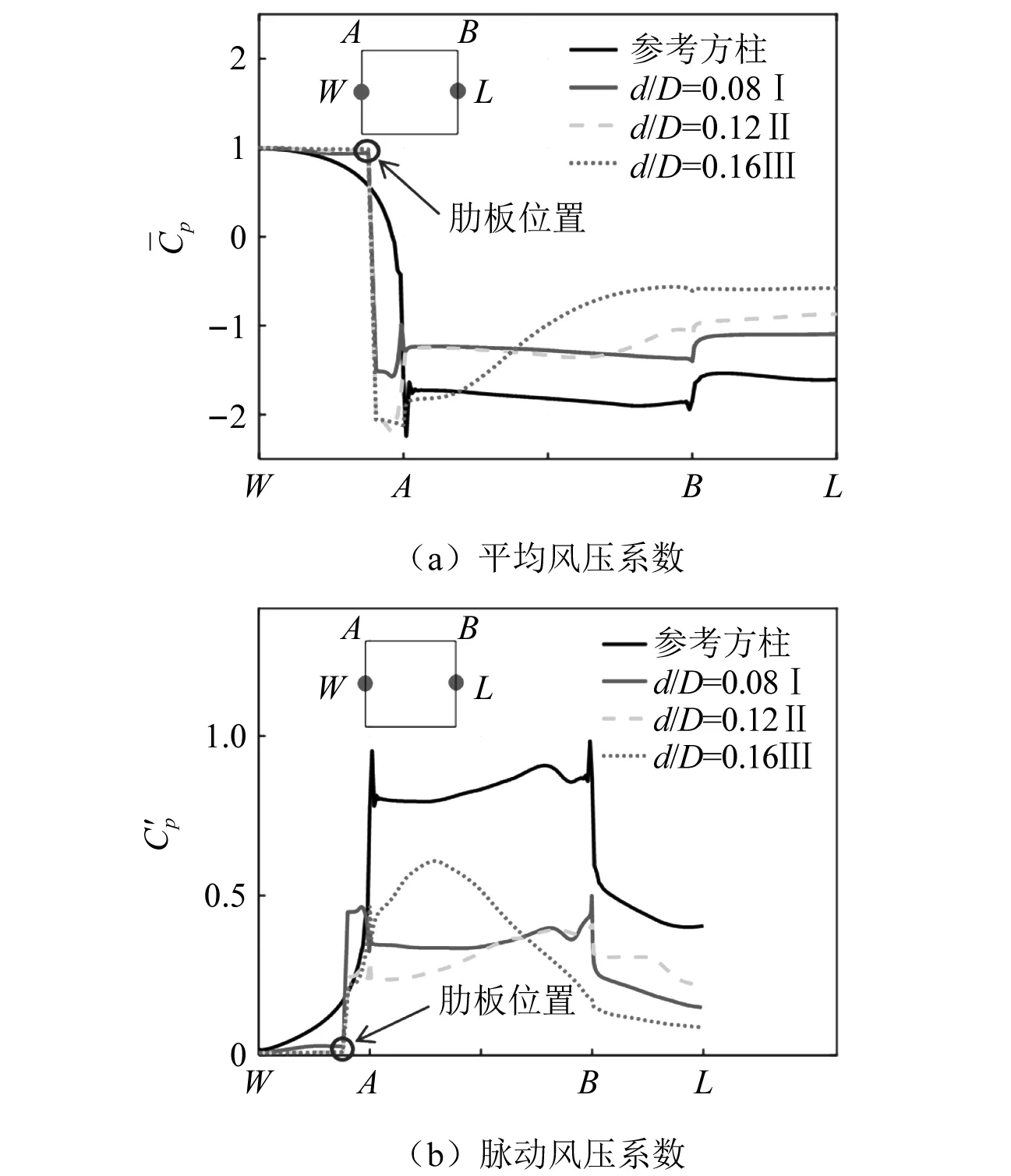
无量纲压力系数Cp、阻力系数Cd和升力系数Cl定义为
(6)
(7)
(8)
式中:p为方柱表面压力;p∞为参考压力;ρ为空气密度;Fd,Fl分别为总阻力和总升力;LZ为方柱展向长度。
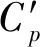
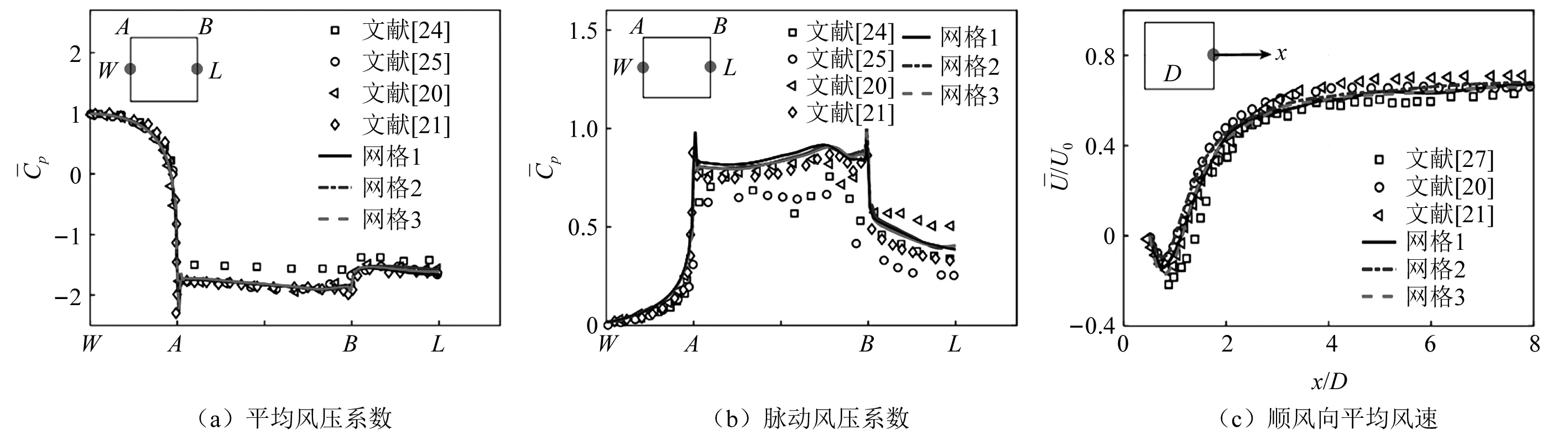
图3 方柱压力和速度分布及验证Fig.3 Comparison of pressure and velocity distributions with the previous studies
表3验证了全局参数结果,包括气动力、斯特劳哈尔数(St=fD/U0,f为涡脱频率)、尾流形成长度(Lf)等。结果表明,尽管模拟和试验条件相似,但不同研究的结果差异明显。本次的LES结果在合理的范围内,表明模拟结果是可靠的。
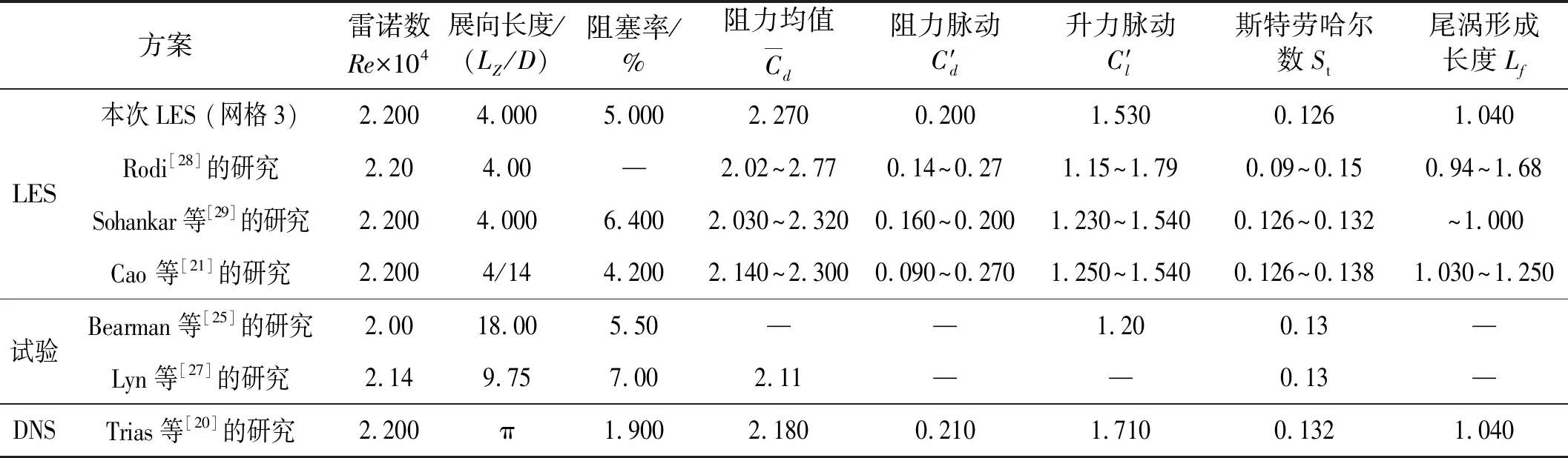
表3 参考方柱LES结果及验证
2 外伸长度的影响
2.1 平均流场结构
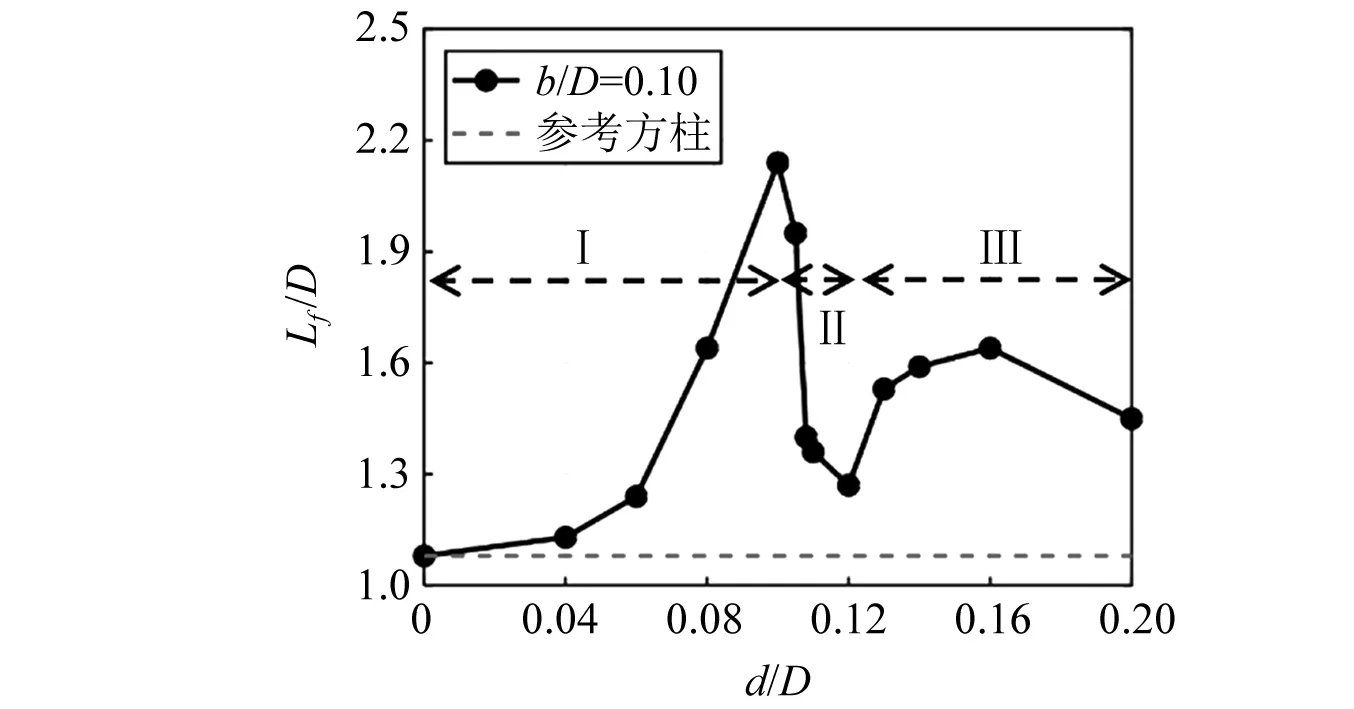
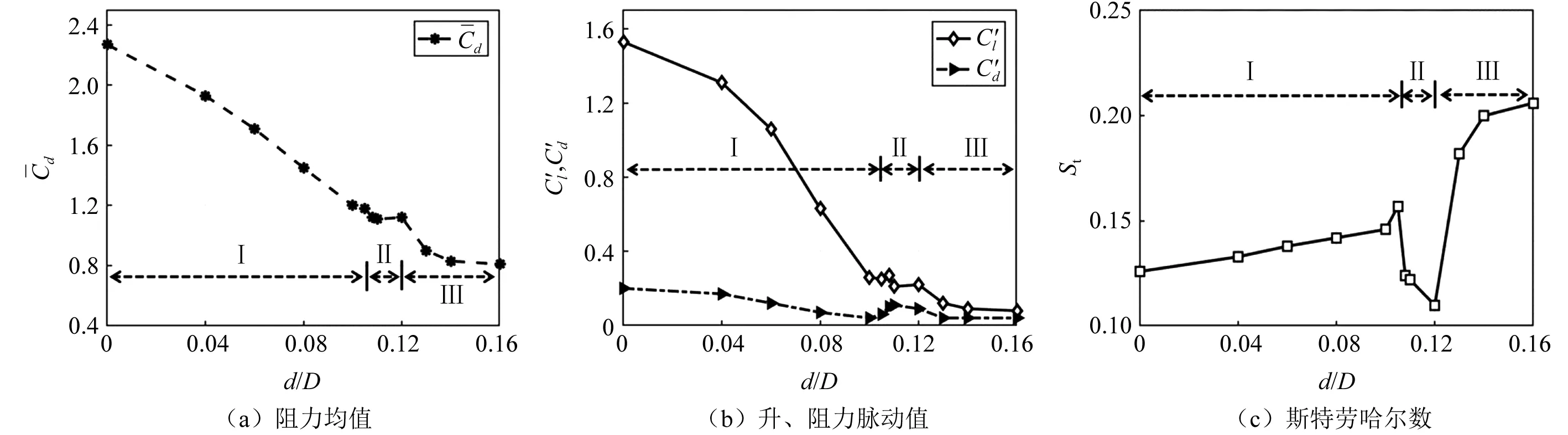
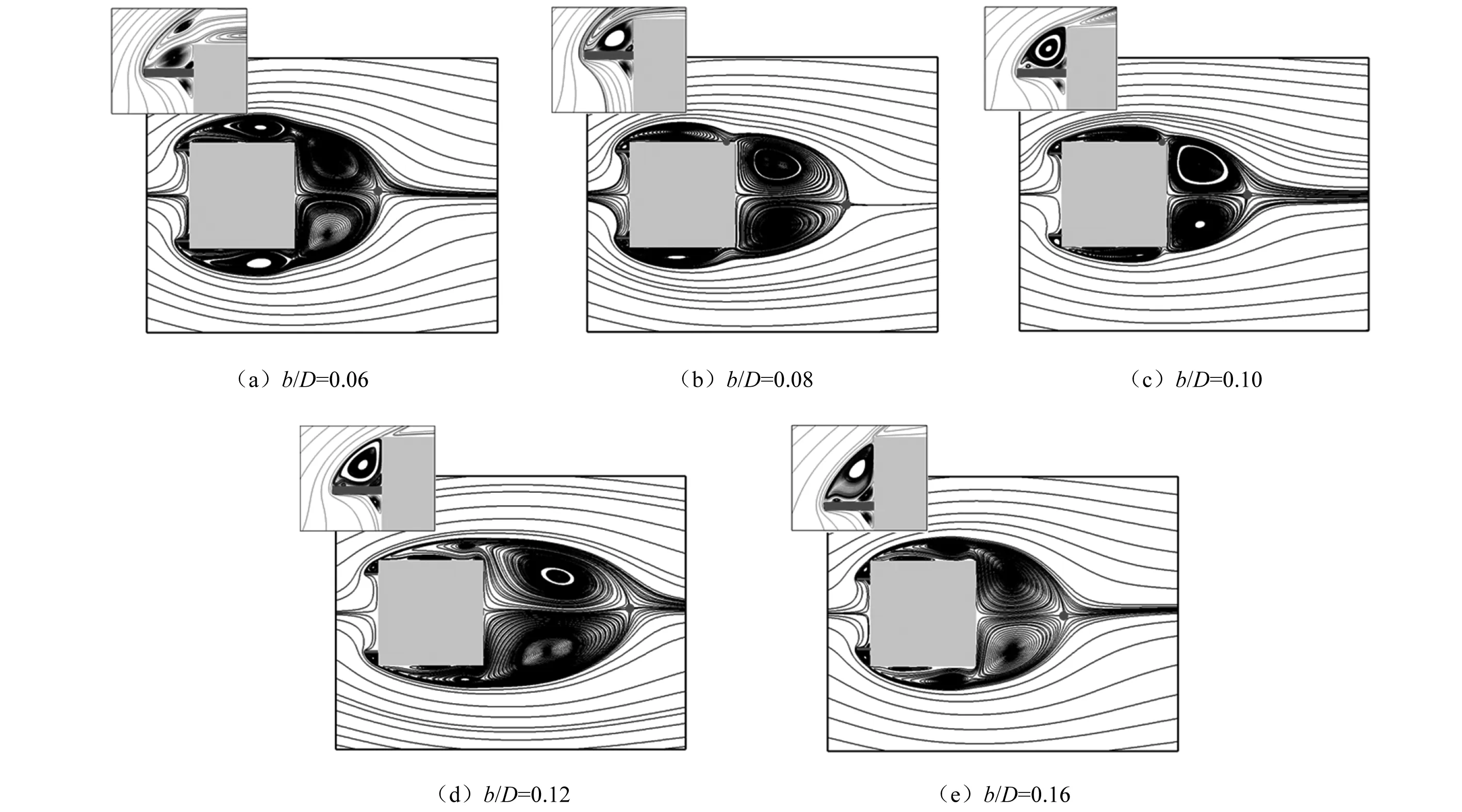
图4展示了外伸长度d对模型周围平均流场的影响,肋板的位置b/D=0.10。可以看出,来流先从肋板的前缘分离,再在模型迎风角区域形成小的局部旋涡。不同外伸长度的肋板对分离剪切层、局部旋涡形状和平均流动结构产生不同的影响。由图4(b)可知,当肋板较短时(d/D≤0.06),前角旋涡呈扁平状,分离流会再附到迎风面。此时外伸板对平均流场影响较小(见图4(a)),可以看到尾涡被略微拉长。当肋板长度增大时(0.060 图4 不同肋板长度下模型周围平均流线(b/D=0.10)Fig.4 Mean streamlines around cylinders with different d at b/D=0.10 由图4(c)~图4(d)可知,当d进一步增加(0.105 图5用尾涡形成长度Lf进一步量化分析肋板长度d对尾涡尺寸的影响,Lf表示为从横截面中心到尾部驻点的水平距离,见图4(a)。由图5可以看出,参考方柱Lf最小。当肋板较短时Lf略微增大(d/D≤0.06)。当0.06 图5 不同外伸长度下模型的尾涡形成长度LfFig.5 Wake formation length Lf of cylinders with different d 由上述平均流场结果可知,不同外伸长度d的肋板模型周围流场呈现3种典型的流动模式:即完全分离流(Ⅰ型,0 图6 模型表面风压分布(b/D=0.10)Fig.6 Wind pressure distribution on cylinder surfaces for b/D=0.10 图7 外伸长度对气动力和斯特劳哈尔数的影响Fig.7 Effect of extension depth d on aerodynamic forces and Strouhal number 图7(c)为模型的斯特劳哈尔数(St)与外伸长度的关系图。由图7(c)可知,竖向肋板会显著改变模型的涡脱频率,St为d的函数。图7(c)中,St在d/D=0.105和 0.120时突然下降和上升,这两个值是本研究中的3种流动模式类型的分界点,表明流动模式的变化导致了St的突然变化。在Ⅰ型流动中,随着肋板长度的增加,St从0.126开始逐渐增加。然而,在Ⅱ型流动中,当d/D=0.120时,St下降至0.110。在Ⅲ型流动中,剪切层的稳定再附使St跃升到较大的值。当d/D=0.160时,St最大达到0.210。 图8 位置参数b对气动力的影响Fig.8 Effect of location parameter b on aerodynamic forces 表4 最优布局参数和最优气动力 图9 模型周围平均流线(d/D=0.12)Fig.9 Mean streamlines around cylinders of d/D=0.12 为阐明竖向肋板的作用机理,在雷诺数Re=2.2×104时,采用LES方法研究迎风面肋板对方柱流场和气动力的影响。通过大量模拟分析了流场信息、风压分布和气动荷载。得出以下结论。 (1) 外伸竖板的存在使模型前角区域产生了局部旋涡,该旋涡明显影响模型周围的流场结构。不同外伸长度d的肋板模型周围流场呈现3种典型的流动模式:即完全分离流(0 (2) 流动模式也影响模型表面的压力分布。在Ⅰ型流动中,虽然,带板模型的压力分布与参考方柱的压力分布基本一致,但随着d的增加,侧壁面和背风面风压的减小趋势逐渐显著。在Ⅱ型流动中,剪切层的周期性再附,使侧壁面后缘附近观察到压力恢复现象。这种压力恢复在Ⅲ型模式中更加明显。同时,剪切层的稳定再附导致侧壁面的脉动风压出现了局部峰值。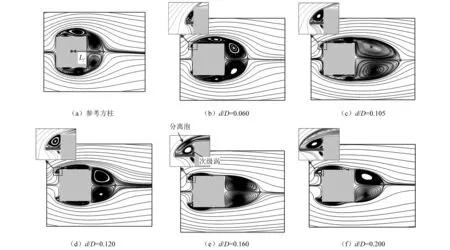
2.2 风压、风荷载和涡脱特征
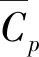
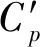
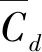
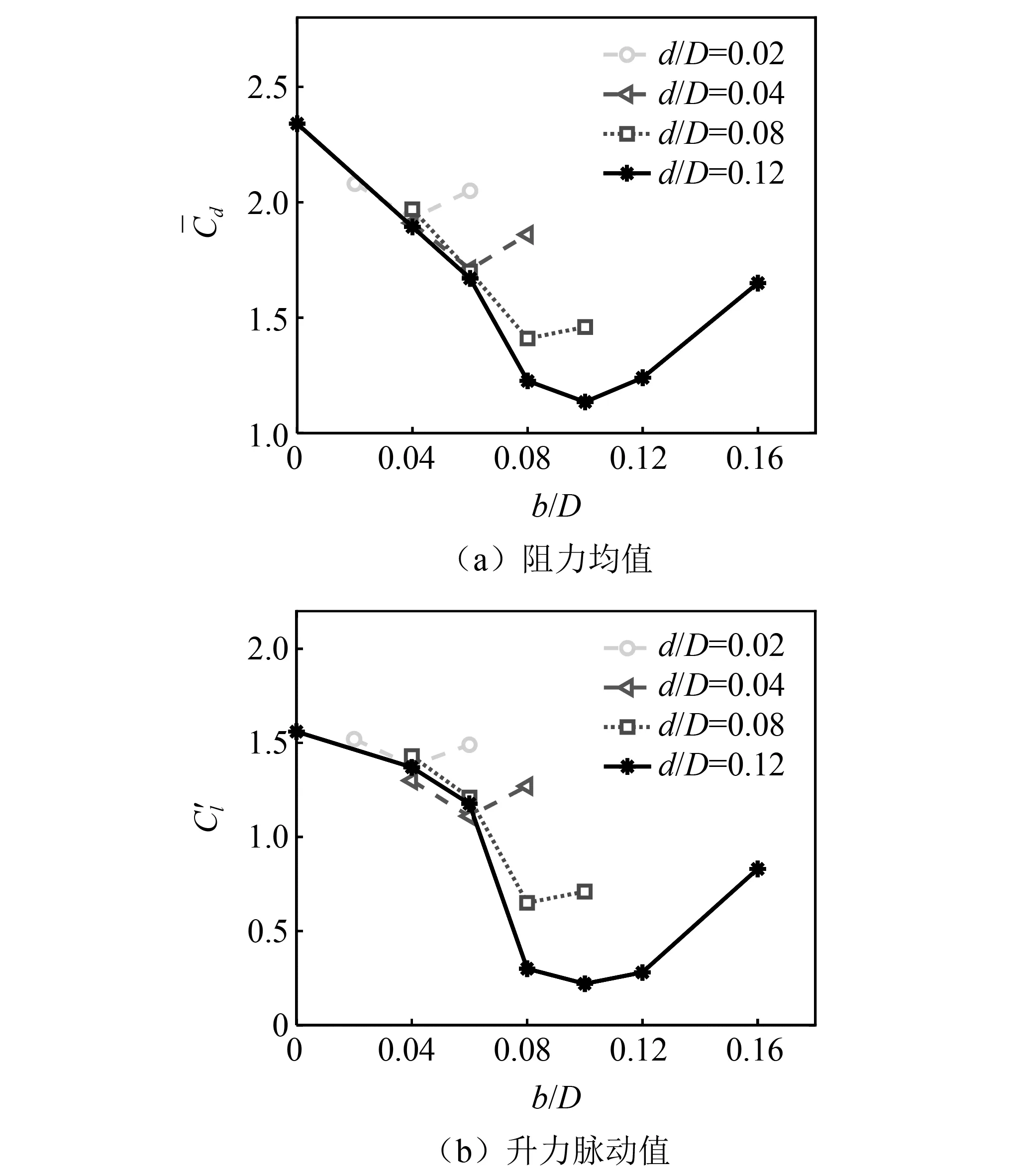
3 肋板的布局优化
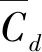
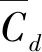

4 结 论