基于Johnson接触模型的内啮合直齿轮系统多状态啮合动力学建模与分析
马晓婧, 石建飞, 张天临, 党兴武, 张 力
(1. 兰州理工大学 机电工程学院,兰州 730050;2. 兰州兰石石油装备工程股份有限公司,兰州 730000)
内啮合齿轮具有中心距小,磨损轻,传动平稳,使用寿命长等[1]特点。由于单齿和双齿之间周期性交替啮合以及齿侧间隙的存在,伴随着转速和载荷的变化,齿轮啮合时出现齿面啮合、轮齿脱离、齿背啮合等多状态啮合行为。准确的解释齿侧间隙所引起的多态啮合行为可为齿轮结构设计优化提供理论指导。目前,齿轮之间的啮合力主要通过线性弹簧阻尼模型计算,该模型由质量单元、弹簧单元和阻尼单元所组成[2]。在涉及长周期且存在冲击时,法向啮合力的变化可为系统动态冲击分析提供基础。基于Hunt等[3]的早期工作,Lankarani等[4]提出改进啮合力模型,该模型解释了传动过程中所发生的能量耗散。Kahraman等[5]早些时候将其用于分析结合误差激励的单自由度齿轮系统的动力学特性。Nevzat等[6]对齿轮非线性动力学模型进行综述,为分析齿侧间隙对齿轮啮合过程的影响奠定了基础。Liu等[7]基于线性弹簧阻尼系统的振荡衰减周期,获得了用于描述啮合过程中能量损失的线性模型中的阻尼项。Chen等[8]将齿侧间隙和齿面摩擦相结合,进行了齿轮非线性动力学特性分析。而单齿和双齿交替啮合特性的研究主要集中在齿轮的时变啮合刚度。Huang等[9]考虑单齿和双齿啮合特性的影响,基于能量法推导了直齿轮系统时变啮合刚度的分析模型。苑士华等[10]计算弹流润滑状态下的圆柱齿轮啮合特性,分析了不同运行参数对摩擦力和啮合力的影响。向玲等[11]综合动态侧隙、齿面摩擦、齿轮偏心及时变啮合刚度等因素,建立了齿轮-转子-滚动轴承系统的弯扭耦合非线性动力学模型。石建飞等[12]推导了在齿侧间隙影响下的齿面啮合、脱啮和齿背啮合3种动力学模型。恒定的齿隙可以清楚地描述齿轮系统的齿面啮合、轮齿分离和齿背啮合,但它不能有效区分齿面或齿背啮合时的单齿和双齿啮合。然而,这可以通过时变齿隙来准确识别单双齿啮合情况[13]。Li等[14]建立了具有动态齿隙的齿轮系统在内外组合周期激励下的非线性动力学模型。Wang等[15]基于有限元法建立了考虑齿轮几何误差和中心距偏差的时变齿隙模型。在以往齿轮系统中,动态啮合力模型被表征为隐式函数。因此,在非线性动力学分析中,需要通过数值迭代来计算每个时间步长内的啮合力。这不仅使其计算成本增高,对计算程序的性能也有考验且因齿轮的法向啮合力是实际工程应用中阻尼的重要来源,以往模型并没有将传动过程中的能量耗散计入其中。在目前有关齿轮系统的非线性动力学研究文献中,尚未见到考虑多状态啮合行为对渐开线内啮合直齿轮系统影响的报道。随着考虑的因素越来越全面、工况越来越复杂,应根据不同啮合状态下齿轮齿廓、啮合线和受力情况分段建立各个啮合状态下齿轮系统动力学模型。
本文在考虑齿面摩擦对齿轮系统的影响,基于Johnson接触力模型,提出了一种计入能量耗散的改进渐开线内啮合直齿轮传动系统动力学动态啮合力计算模型。在该啮合力模型中,克服了目前现有模型的局限性,在考虑冲击过程中的能量耗散下,将动态啮合力定义为显式函数。同时,基于渐开线内啮合圆柱直齿轮传动原理、时变齿隙以及轮齿间的受力情况,分别建立齿轮副系统在单齿齿面啮合、双齿齿面啮合、单齿齿背啮合、双齿齿背啮合和轮齿脱离多状态下的动力学模型。该研究可为齿轮传动系统的动态性能优化、参数设计和进一步研究提供了有益的参考。
1 时变参数的计算
1.1 基于Johnson接触模型的动态啮合力
齿轮啮合力的确定是预测齿轮传动系统动态性能和承载能力的关键。对齿轮系统进行动态特性分析时,大多数啮合力模型是基于Hertz压力,具有Hertz接触理论[16]的限制性,迫使这类模型只能用于低间隙的啮合条件。传统模型将啮合力表示为隐函数的数学形式,使其在实际应用中计算成本偏高。
本文中动态啮合力计算模型基于Johnson接触力模型[17]而改进。在齿轮啮合时,啮合轮齿间会产生碰撞或冲击行为而导致能量的散耗。Lankarani等建立了计入能量耗散的啮合力模型,提出用恢复系数ce进行修正,并证实了该系数的有效性。同时,将啮合力定义为显式函数,消除低间隙的使用限制且计算更简便,由(1)式计算得到。
(1)
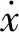
(2)
(3)
(4)
式中, ΔR为齿侧间隙,式(4)中常数Y为对于内部接触难以找一个单一表达式来获得良好拟合,即Y可表示为
(5)
综上,可以得到齿轮副啮合力数学表达式,如式(6)所示
(6)
(7)
式中,i=k,d分别为齿轮齿面和齿背。
1.2 基于弹流润滑理论的摩擦因数
齿面摩擦因数主要受轮齿几何形状、表面硬度、接触压力和齿面相对滑动速度等因数的影响。本文考虑弹流润滑下的摩擦因数。根据He等[18]的研究,第i对啮合齿轮副的时变摩擦公式表示为式(6)。
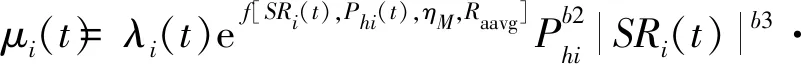
(8)
f[SRi(t),Phi(t),ηM,Raavg]=b1+b9eRaavg+
b4|SRi(t)Phi(t)lgηM|+b5e-|SRi(t)Phi(t)lg ηM|
(9)
式中,Raavg=(Ra1+Ra2)/2为平均表面粗糙度;ηM=0.058为动态黏度;bi(i= 1,2,…,9)为经验因子,其值参见Chen等的研究。第i对啮合齿轮的最大赫兹压力Phi(t)表示为式(10)
(10)
式中:fe=Tp/bRbpcosα为单位法向载荷;ρri(t)为第i对啮合齿轮的相对曲率半径。
在式(8)、式(9)中,无量纲滚滑率SRi(t)=2vs(t)/ve(t),vs(t)为齿面滑移速度,ve(t)为卷吸速度。λi(t)为摩擦力的方向系数,可通过式(11)得到。
λi(t)=sgn[vs(t)]
(11)
式中, sgn(·)为符号函数,用于确定摩擦力的方向。
2 内啮合齿轮系统多状态啮合动力学模型
在低速重载的条件下,齿轮系统处于齿面啮合状态。在高速轻载的条件下,齿隙会引起周期性的轮齿脱离或齿背啮合行为。为了更好地理解齿轮传动系统的多状态啮合特性,假设齿轮副为刚性支承,只考虑齿轮的扭转振动,渐开线内啮合圆柱直齿轮在齿面和齿背啮合状态下简化的物理模型如图1所示。

图1 齿轮副的简化物理模型Fig.1 A simplified physical model about gear
该模型中主、从动轮的转动角位移分别为θp和θg,转动惯量分别为Ip和Ig,齿侧间隙为D(τ),齿面啮合刚度和阻尼分别为KK,CK,齿面摩擦因数为μK;齿背啮合刚度和阻尼分别为Kd,Cd及齿背摩擦因数为μd;齿轮副动态传递误差为e(τ),其中齿面误差激励e(τ)=eK(τ),齿背误差为激励e(τ)=ed(τ)。其余算例参数如表1所示。
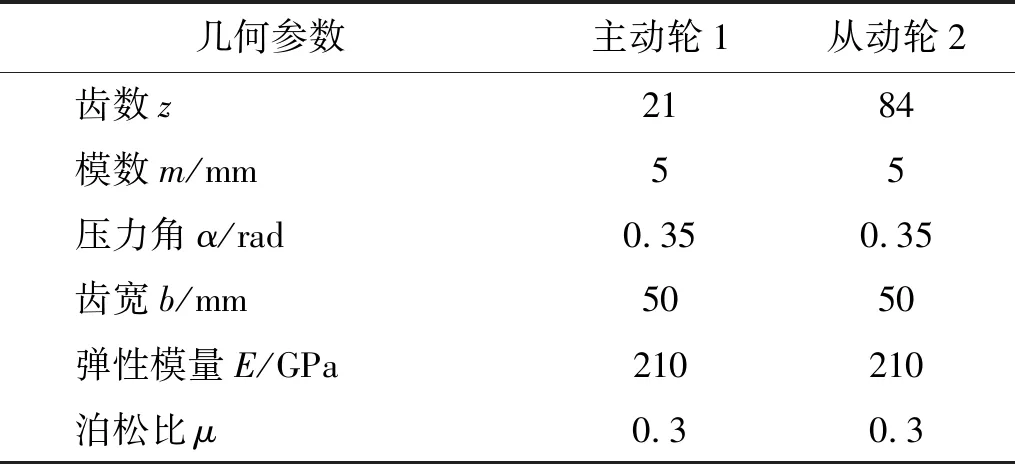
表1 齿轮参数表Tab.1 Gear parameter table
2.1 内啮合直齿轮系统多状态啮合分类
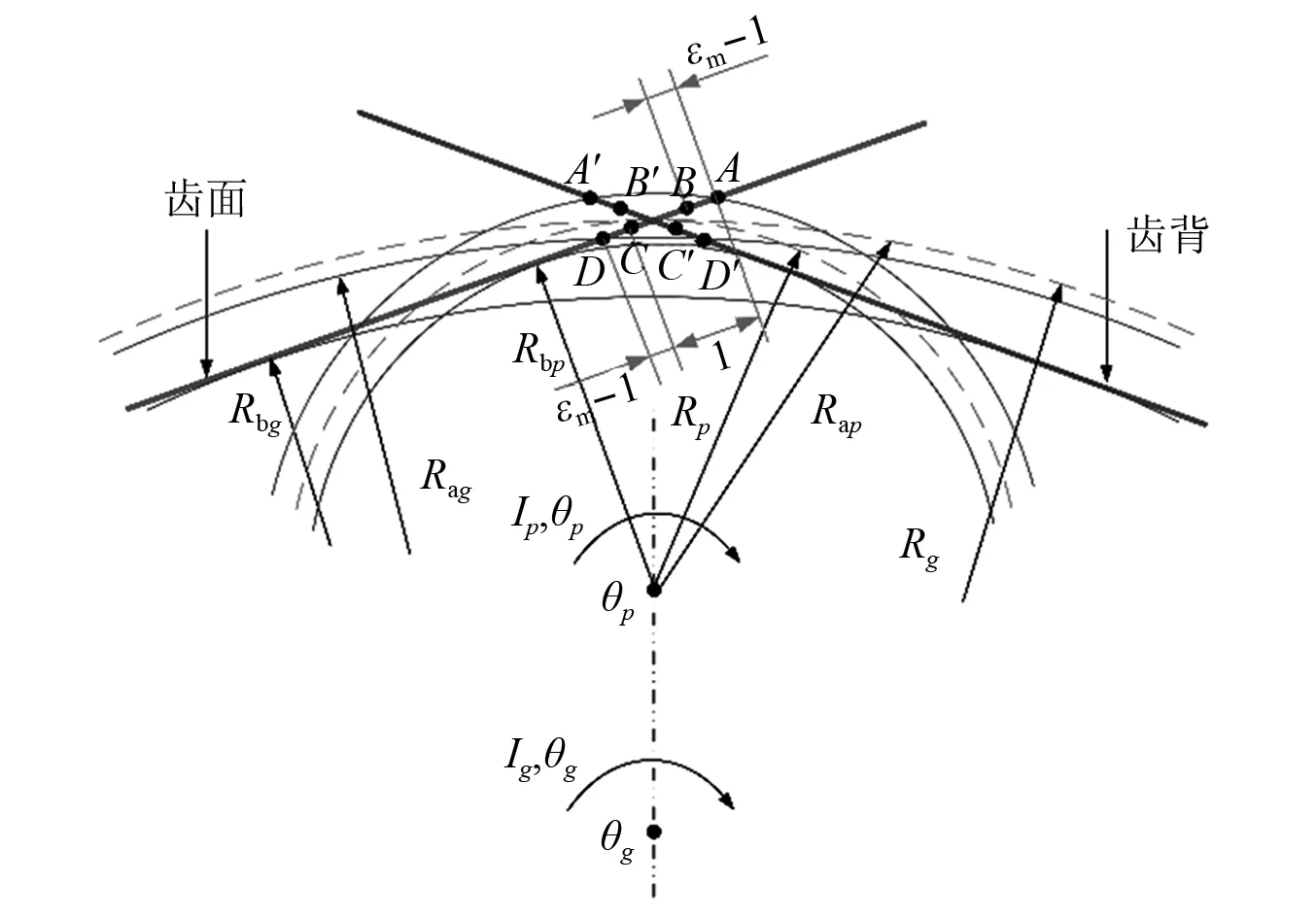
图2 内啮合直齿轮的齿面和齿背啮合示意图Fig.2 A meshing schematic diagram of a spur gear pair with drive-side and back-side tooth meshes
基于啮合过程中啮合点的位置以及相对位移量与齿侧间隙的几何关系,齿轮啮合状态及其边界条件可分为:
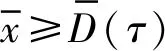
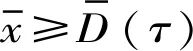
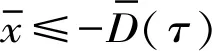
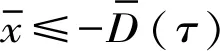
式中:Tm=2π/(zpωp)为一个完整的啮合周期,包括单齿和双齿啮合(AC或A′C′);zp,ωp分别为主齿轮的齿数和旋转角速度。根据上述5种啮合状态,分别建立相应的动力学模型如下。
2.2 系统多状态啮合动力学建模
2.2.1 双齿齿面啮合状态
双齿齿面啮合状态下啮合点处受力分析图,如图3所示。有两对轮齿同时参与啮合,由于存在加工误差及轮齿的变形,所以对工作区内两对齿所受载荷的分配有所变化。FNp1,FNp2,FNg1和FNg2为作用在主、从动齿轮上的法向正压力,方向沿着啮合线方向。Ffp1,Ffp2,Ffg1和Ffg2为作用在主、从动齿轮上的摩擦力,方向垂直于啮合线方向。
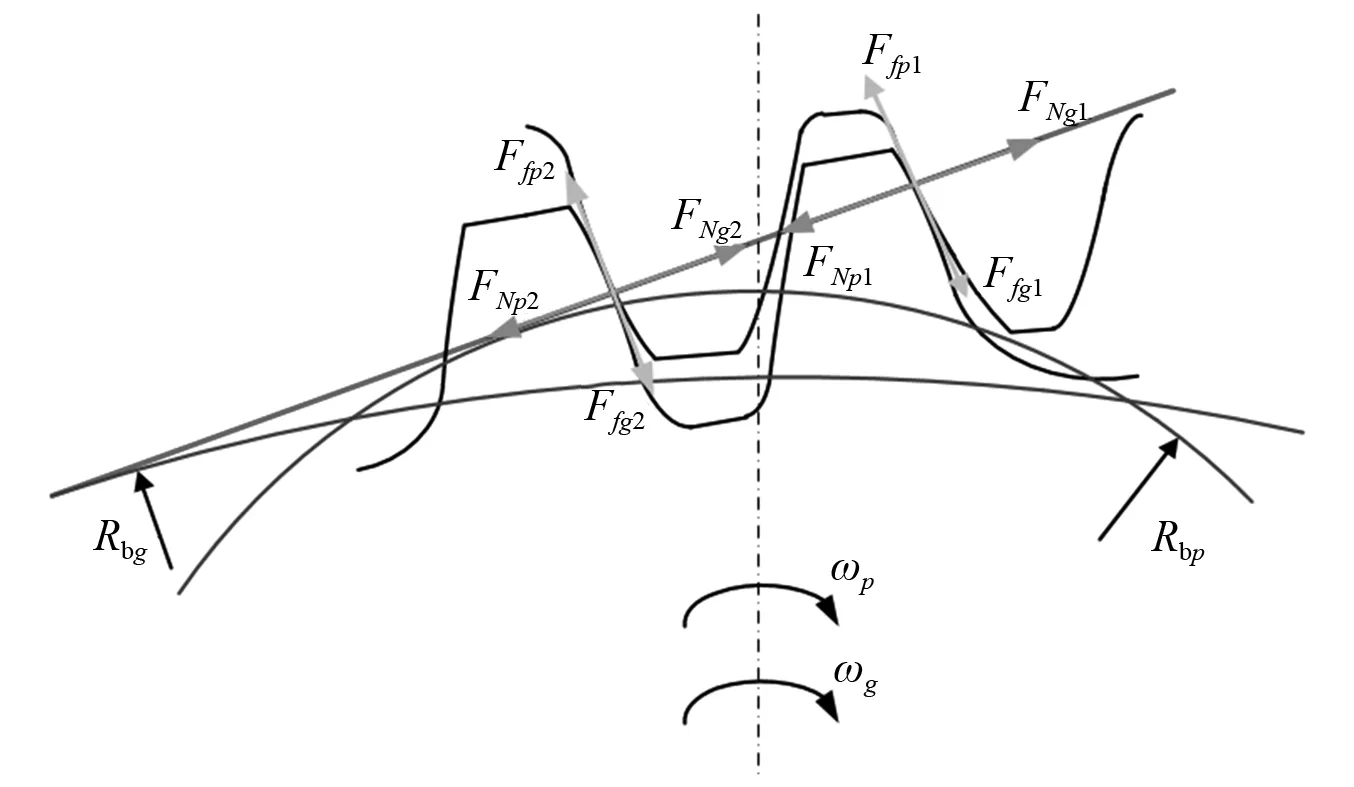
图3 双齿齿面啮合状态下啮合点处受力分析图Fig.3 A schematic diagram of force analysis of the spur gear pair under double-tooth drive-side meshing state
根据内啮合齿轮传动原理和第二牛顿定律,可得双齿齿面啮合状态下主、从动轮的绝对转动方程
(12)
式中,两轮齿齿面法向正压力FNp1,FNg1,FNp2和FNg2,可由式(13)计算得到。式(14)中,Fm为作用在两轮齿啮合力,可由式(6)计算得到。
FNp1>=FNg1>=Lk1(τ)Fm,FNp2>=FNg2>=Lk2(τ)Fm
(13)
式中,Lk1(τ),Lk2(τ)为负载分担比可由文献[19]得到。作用在两轮齿齿面的摩擦力Ffp1,Ffg1,Ffp2和Ffg2与摩擦因数μki(τ)(i=1,2)和齿面法向正压力成正比,可由式(14)计算得到。
Ffp1=Ffg1=λk1(τ)μk1(τ)Lk1(τ)Fm,
Ffp2=Ffg2=λk2(τ)μk2(τ)Lk2(τ)Fm
(14)
式中,时变摩擦力方向系数λki(τ)与啮合点的位置有关,在节点附近齿面滑移速度方向发生变化,导致摩擦力方向发生变化。故时变摩擦力方向系数λki(τ)与齿面滑移速度vm(t)相关,可由式(11)计算得到。
式(12)中的Sdp1(τ),Sdp2(τ),Sdg1(τ),Sdg2(τ)分别为齿轮副的摩擦力矩,可以写为
(15)
(16)
将式(13)中的两个公式相减,即可得到双齿齿面啮合状态下齿轮系统的相对扭转动力学方程,如式(17)。
(17)

2.2.2 单齿齿面啮合状态
单齿齿面啮合状态下啮合点处受力分析图,如图4所示。FNp2和FNg2是作用在主、从动齿轮上的正压力,方向沿着啮合线方向。Ffp2和Ffg2是作用在主、从动齿轮上的摩擦力,方向垂直于啮合线方向。
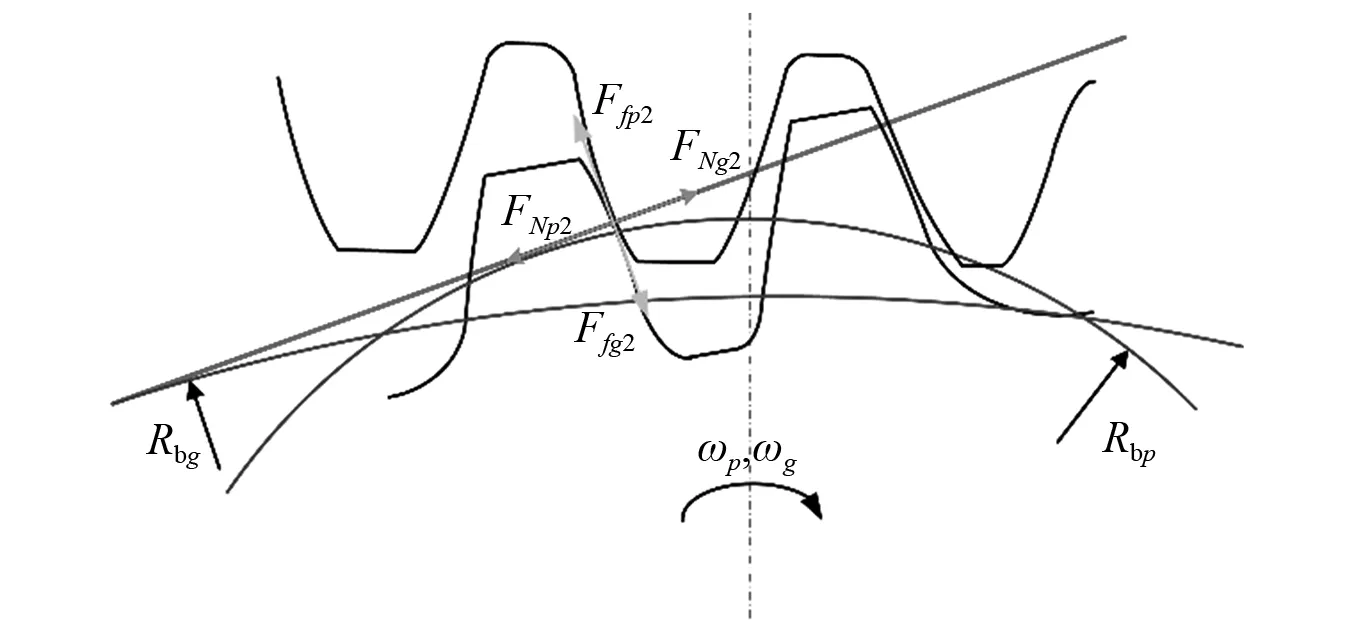
图4 单齿齿面啮合状态下啮合点处受力分析图Fig.4 A schematic diagram of force analysis of the spur gear pair under single-tooth drive-side meshing state
根据内啮合齿轮传动原理和第二牛顿定律,可得双齿齿面啮合状态下主、从动轮的绝对转动方程
(18)
式中,两轮齿齿面法向正压力FNp2和FNg2,可由式(19)计算得到。式(18)中,Fm为作用在两轮齿啮合力,可由式(6)计算得到。
FNp2=FNg2=Fm
(19)
式中,作用在两轮齿齿面的摩擦力Ffp2和Ffg2与摩擦因数μki(τ)和齿面法向正压力成正比,可由式(20)计算得到。
Ffp2=Ffg2=λk2(τ)μk2(τ)Fm
(20)
将式(18)中的两个公式相减,即可得到单齿齿面啮合状态下齿轮系统的相对扭转动力学方程,如式(18)所示。
(21)
2.2.3 双齿齿背啮合状态
双齿齿背啮合状态下啮合点处受力分析图,如图5所示。有两对轮齿同时参与啮合过程,由于存在加工误差及轮齿的变形,所以对工作区内两对齿所受载荷的分配有所变化。FNp1,FNp2,FNg1和FNg2为作用在主、从动齿轮上的正压力,方向沿着啮合线方向。Ffp1,Ffp2,Ffg1和Ffg2为作用在主、从动齿轮上的摩擦力,方向垂直于啮合线方向。
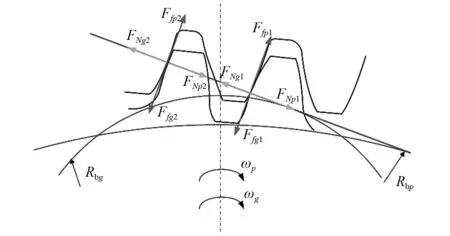
图5 双齿齿背啮合状态下啮合点处受力分析图Fig.5 A schematic diagram of force analysis of gear teeth under double-tooth back-side meshing state
根据内啮合齿轮传动原理和第二牛顿定律,可得双齿齿背啮合状态下主、从动轮的绝对转动方程
(22)
式中,两轮齿齿面法向正压力FNp1,FNg1,FNp2和FNg2,可由式(23)计算得到。式(23)中,Fm为作用在两轮齿啮合力,可由式(6)计算得到。
FNp1>=FNg1>=Ld1(τ)Fm,FNp2>=FNg2>=Ld2(τ)Fm
(23)
式中,Ld1(τ),Ld2(τ)为负载分担比可由Pedrero等的研究得到。作用在两轮齿齿面的摩擦力Ffp1,Ffg1,Ffp2和Ffg2与摩擦因数μdi(τ)(i=1,2)和齿面法向正压力成正比,可由式(24)计算得到。
Ffp1=Ffg1=λd1(τ)μd1(τ)Ld1(τ)Fm,
Ffp2=Ffg2=λd2(τ)μd2(τ)Ld2(τ)Fm
(24)
式中,时变摩擦力方向系数λdi(τ)与啮合点的位置有关,在节点附近齿面滑移速度方向发生变化,导致摩擦力方向发生变化。故时变摩擦力方向系数λdi(τ)与齿面滑移速度vm(t)相关,可由式(11)计算得到。
式(22)中的Sdp1(τ),Sdp2(τ),Sdg1(τ),Sdg2(τ)分别为齿轮副的摩擦力矩,可以写为
(25)
(26)
将式(24)中的两个公式相减,即可得到双齿齿面啮合状态下齿轮系统的相对扭转动力学方程,如式(27)所示。
(27)
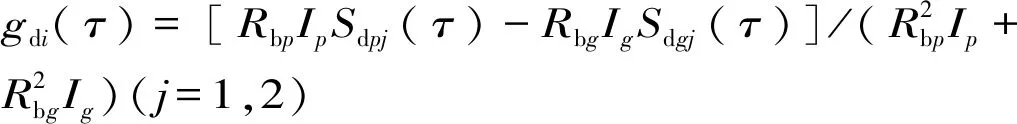
2.2.4 单齿齿背啮合状态
单齿齿背啮合状态下啮合点处受力分析图,如图6所示。有一对轮齿同时参与啮合过程。FNp2和FNg2为作用在主、从动齿轮上的正压力,方向沿着啮合线方向。Ffp2和Ffg2为作用在主、从动齿轮上的摩擦力,方向垂直于啮合线方向。
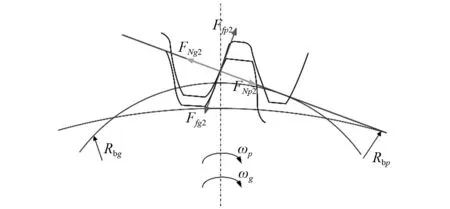
图6 单齿齿背啮合状态下啮合点处受力分析图Fig.6 A schematic diagram of force analysis of gear teeth under single-tooth back-side meshing state
根据内啮合齿轮传动原理和第二牛顿定律,可得单齿齿背啮合状态下主、从动轮的绝对扭转方程
(28)
式中,两轮齿齿面法向正压FNp1,FNg1,FNp2和FNg2,可由式(29)计算得到。式(29)中,Fm为作用在两轮齿啮合力,可由式(6)计算得到。
FNp2=FNg2=Fm
(29)
式中,作用在两轮齿齿面的摩擦力Ffp2和Ffg2与摩擦因数μdi(τ)和齿面法向正压力成正比,可由式(30)式计算得到。
Ffp2=Ffg2=λd2(τ)μd2(τ)Fm
(30)
将式(28)中的两个公式相减,即可得到双齿齿面啮合状态下齿轮系统的相对扭转动力学方程,如式(31)所示。
(31)
2.2.5 轮齿脱离状态
脱齿状态示意图,如图7所示。根据内啮合齿轮传动原理和第二牛顿定律,可得轮齿脱离状态下主、从动轮的运动学方程
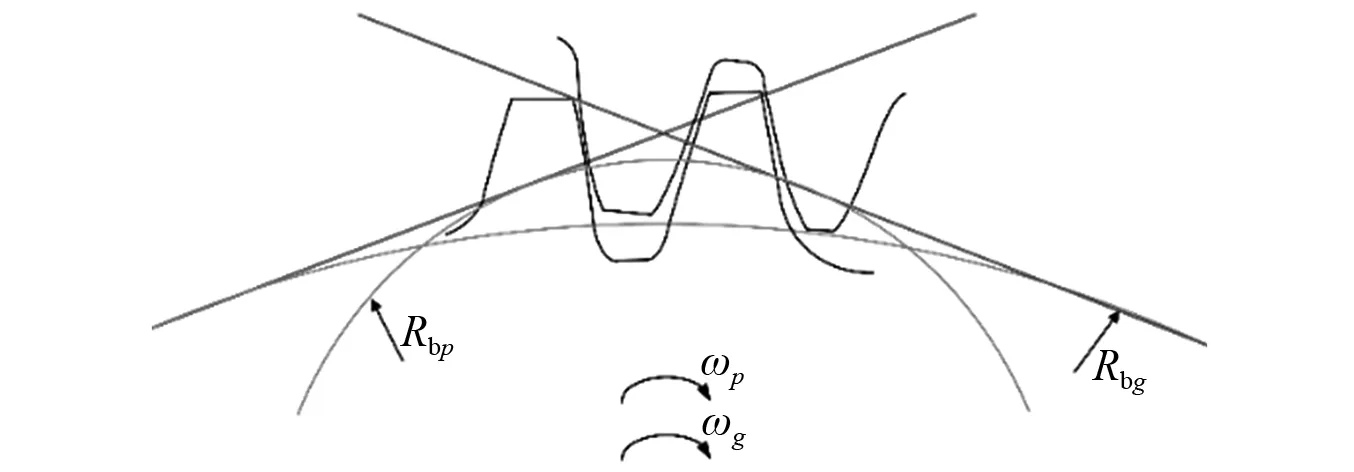
图7 脱齿状态示意图Fig.7 A schematic diagram of the gear pair under teeth disengaged state
(32)
将式(32)中的两个公式相减,即可得到轮齿脱离状态下的动力学方程,如式(33)所示。
(33)
2.3 系统多状态啮合的无量纲归一化模型
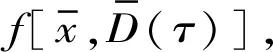
(34)
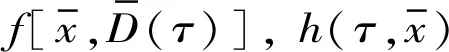
(35)
(36)
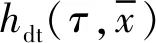
(37)
(38)
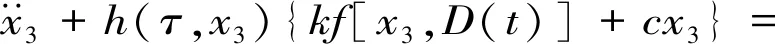
(39)
其中
h(t,x3)=
(40)
hdt(t,x3)=
(41)
(42)
因此,得到包含双齿齿面啮合、单齿齿面啮合、双齿齿背啮合、单齿齿背啮合、轮齿脱离等5种状态的内啮合圆柱直齿轮系统非线性动力学无量纲归一化表达式,如式(39)。该模型为研究齿轮系统的非线性动力学和多态啮合行为提供了模型基础。
3 系统多状态啮合行为辨识与分析
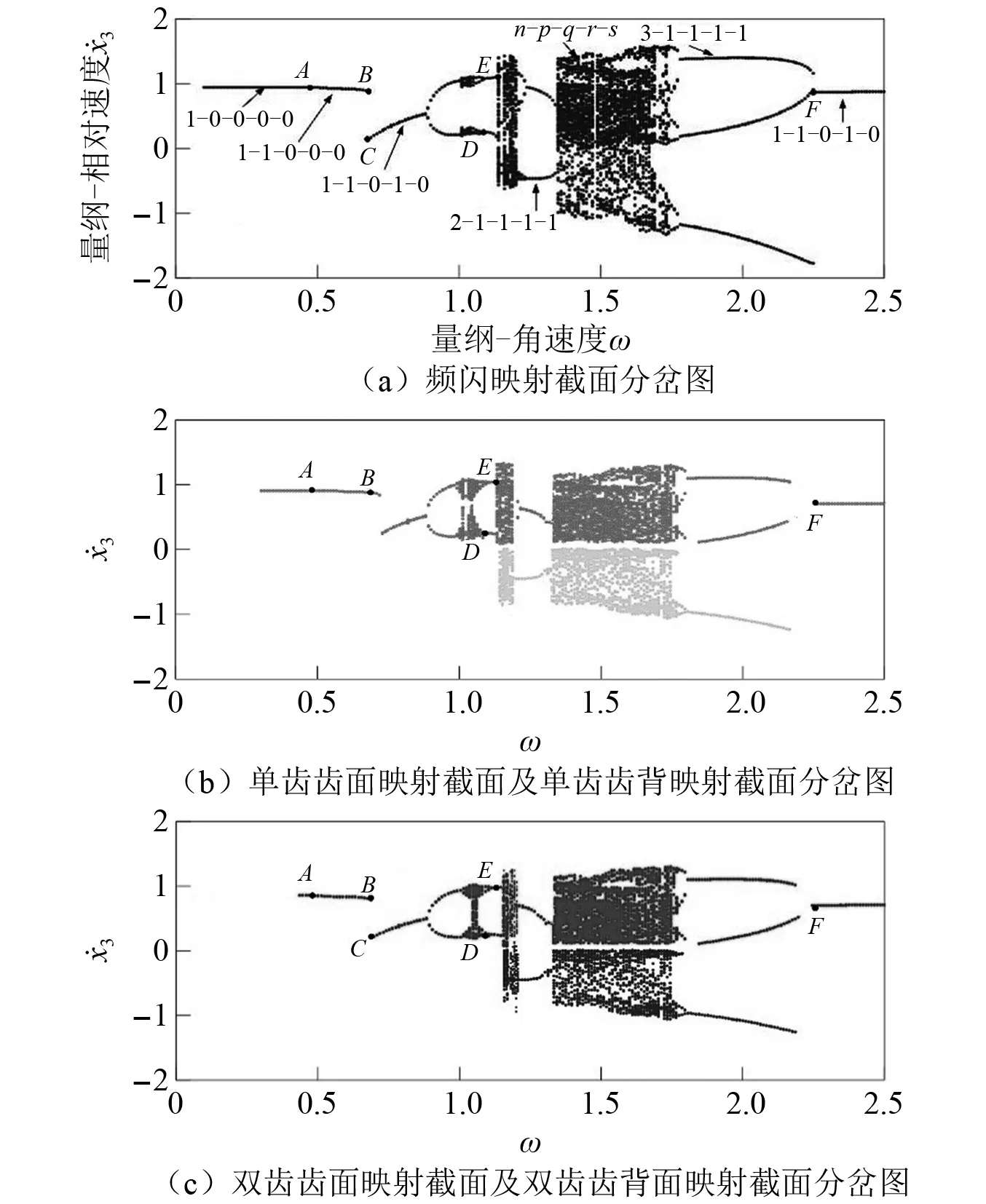
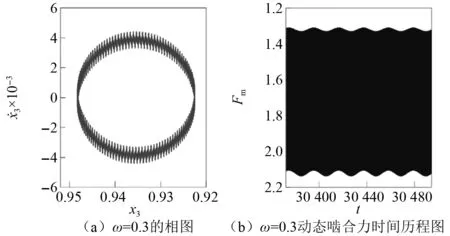
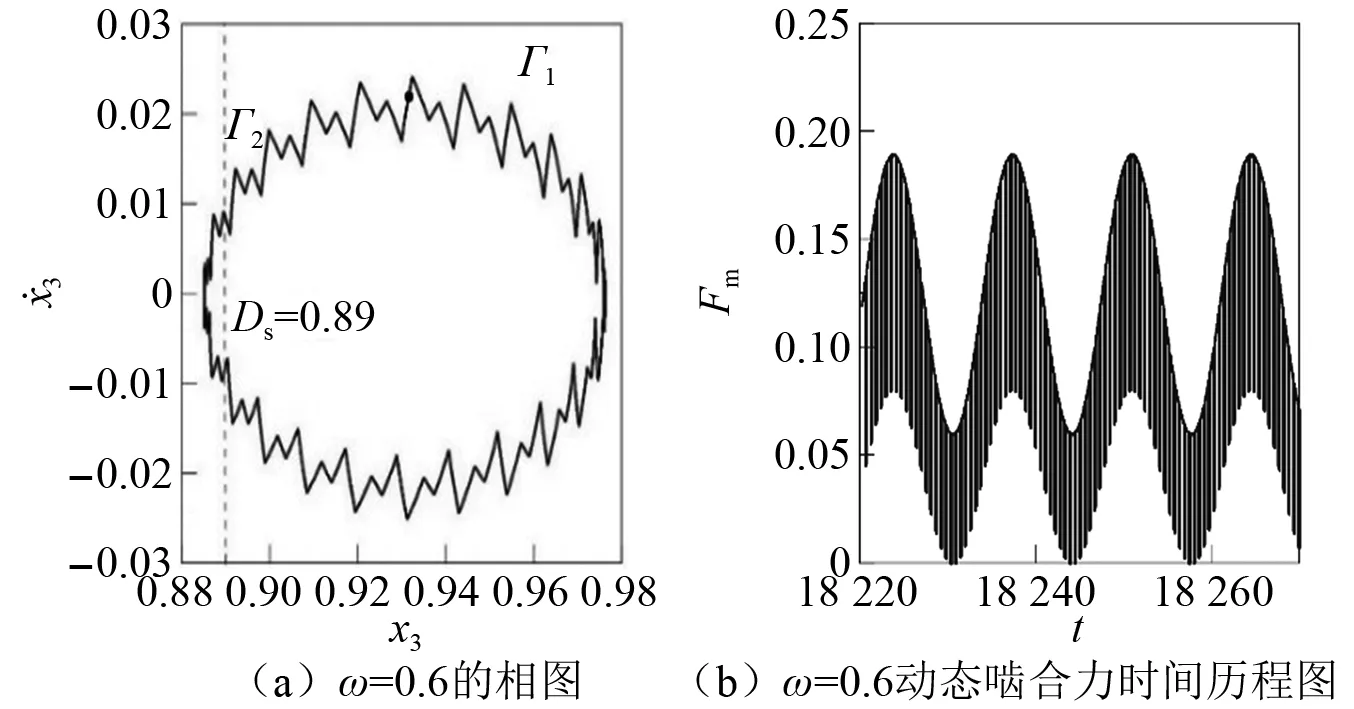
通过第2章的分析,得到渐开线内啮合圆柱直齿轮多状态啮合的动力学模型。因此,根据轮齿间相对位移量与齿隙的数值关系,可以观察到相平面内五态啮合行为的存在区域。通过时变齿隙能够准确辨别工作区内单双齿啮合情况,假设Dd为在双齿啮合区域的无量纲齿隙,Ds为在单齿啮合区域的无量纲齿隙,其中Ds>Dd。
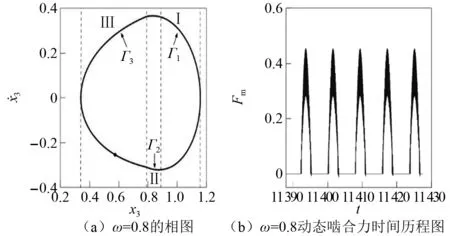
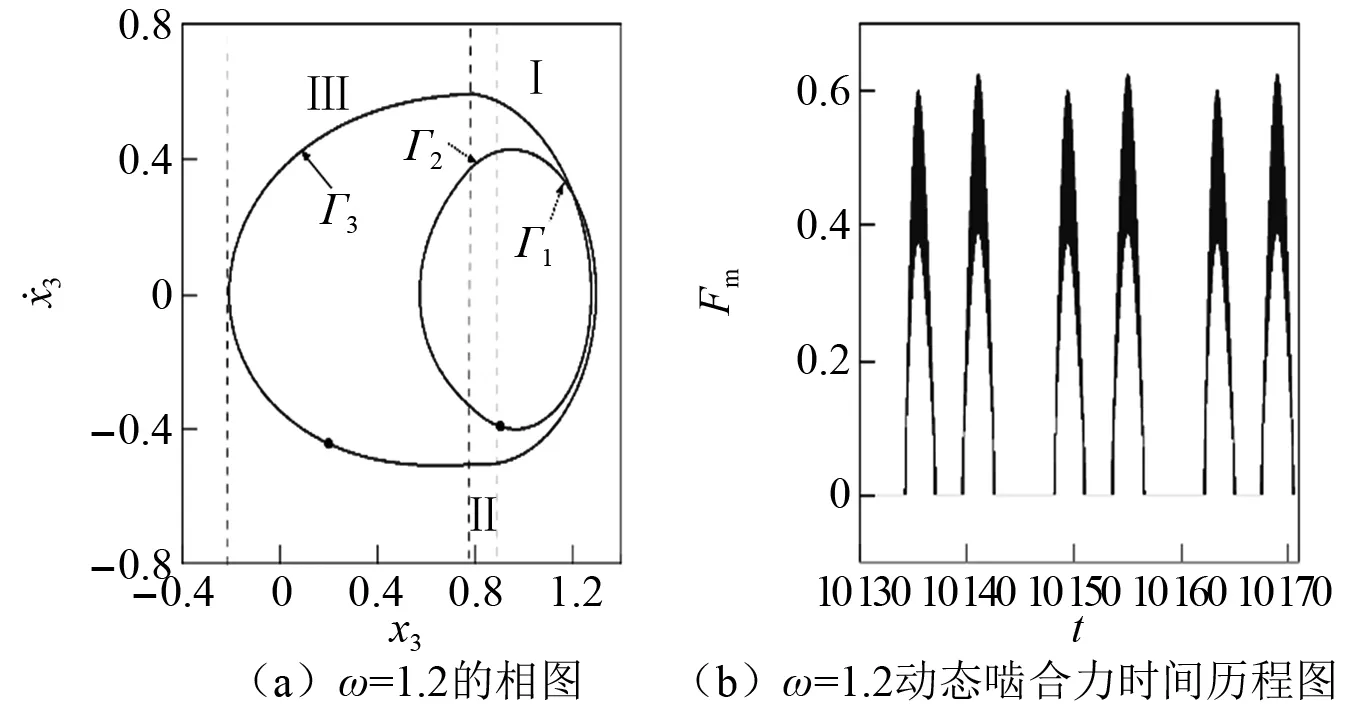
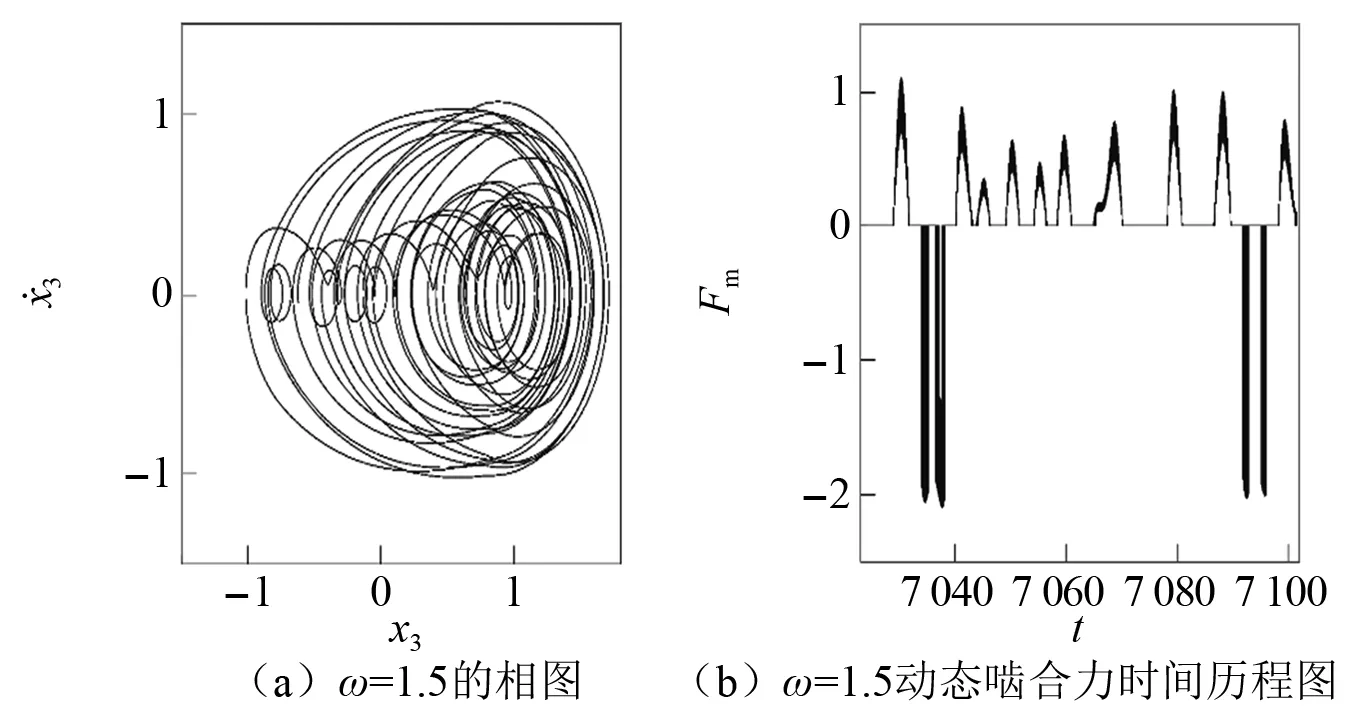
如图8所示,单齿齿面啮合存在于Ⅰ区(x3≥Ds)。单齿脱离存在于Ⅱ∪Ⅲ∪Ⅳ区(|x3| 图8 相平面五态所占面积Fig.8 The existence area of five meshing states in the phase plane 根据上述5种不同的Poincaré映射部分,齿轮系统的多状态啮合运动可以用符号n-p-q-r-s来表示。其中:n为系统周期运动次数;p为单齿齿面啮合次数;q为单齿齿背啮合次数;r为双齿齿面啮合次数;s为双齿齿背啮合次数。若p,q,r或s为零,则表示无单齿齿面啮合、单齿齿背啮合、双齿齿面啮合、双齿齿面背啮合多态啮合的发生。通过分析n-p-q-r-s的运动特性,可得到齿轮系统的多态啮合行为的非线性动力学特性。 设F=0.16,ε=0.23且以啮合频率ω作为控制变量。基于构造的5种不同Poincaré映射,分析啮合频率变化对齿轮系统在弹流润滑下的多状态啮合行为的振动特性。图9(a)深灰色部分为在频闪映射截面Σn下系统随啮合频率逐渐增大的分岔图。图9(b)中深灰色为系统在单齿齿面映射截面Σp的分岔图,浅色为系统在单齿齿背映射截面Σq的分岔图。图9(c)浅灰色部分为双齿齿面映射截面Σr的分岔图,深灰色为双齿齿背映射截面Σs的输出图。 图9 随着ω增加不同Poincaré映射截面的分岔图Fig.9 Bifurcation diagrams in different Poincareé mapping sections with the increase in ω 由图9可知,当啮合频率ω较小时(A点左侧),系统表现为1-0-0-0-0运动,图10(a)和图10(b)分别为ω=0.3的相图和动态啮合力时间历程图。此时系统的动态啮合力始终大于零,表明齿面啮合状态持续存在,且不存在脱啮和齿背啮合。由于振动幅度较小,齿轮系统的轮齿相对位移和相对速度在单齿和双齿之间跳跃更为明显。 图10 相图与动态啮合力时间历程图(1)Fig.10 Phase portraits and time histories of dynamic meshing force (1) 随啮合频率ω逐渐增大(A点和B点之间),系统表现为1-1-0-0-0运动。图11(a)和图11(b)分别为ω=0.6的相图和动态啮合力时间历程图,“·”为Poincaré映射点。在图11(a)中相轨迹跨越了单齿隙值的一半,其中Γ1为单齿和双齿齿面啮合区域,Γ2为单齿脱离和双齿齿面啮合区域。图11(b)为相应的动态啮合力,动态啮合力在单齿区域为零,而双齿区域的动态啮合力始终大于零,表明单齿脱离行为发生存在周期性。 图11 相图与动态啮合力时间历程图(2)Fig.11 Phase portraits and time histories of dynamic meshing force (2) 经过C点后,系统转变为稳定的1-1-0-1-0运动,相轨迹较之前更为平滑但仍然存在单齿和双齿脱离。其中,Γ1为单齿和双齿齿面啮合区域,Γ2为单齿齿背和双齿齿面啮合区域,Γ3为单、双齿脱啮状态,如图12(a)所示。系统的动态啮合力周期性地出现在大于零与等于零之间,如图12(b)所示。 图12 图与动态啮合力时间历程图(3)Fig.12 Phase portraits and time histories of dynamic meshing force (3) 当啮合频率继续增加,齿轮系统由1-1-0-1-0运动通过倍化分岔进入短混沌运动。随后系统转变为周期2运动,主动轮与被动轮的啮合次数增加一倍,表现为2-2-0-2-0运动,其相图和动态啮合力时间历程图如图13所示。 图13 相图与动态啮合力时间历程图(4)Fig.13 Phase portraits and time histories of dynamic meshing force (4) 在D点,齿面啮合、齿背接触以及脱啮的次数发生改变,系统过渡到2-1-1-1-1运动。在E点,经周期倍化分岔再次进入混沌运动,即n-p-q-r-s运动。此时,相轨迹变得杂乱无章且穿过Ds,-Ds,Dd和-Dd,如图14(a)所示;动态啮合力出现小于零和等于零(Fm>0,Fm=0和Fm<0)的情况,如图14(b)所示。表明系统出现单齿齿面啮合、双齿齿面啮合、脱啮、单齿齿背啮合和双齿齿背啮合5种状态啮合行为。 图14 相图与动态啮合力时间历程图(5)Fig.14 Phase portraits and time histories of dynamic meshing force (5) 随着啮合频率进一步增加,系统由混沌运动变为3-1-1-1-1运动。在F点,系统经逆倍化分岔由3-1-1-1-1运动退化为稳定的1-1-0-1-0运动,即系统经F点后发生齿面啮合、单双齿的脱啮等行为。 由以上分析结果可知,当啮合频率ω较小时,系统保持稳定的齿面啮合状态。随着啮合频率ω持续增大,系统逐渐出现单双齿的脱啮、单齿齿背啮合和双齿齿背啮合等多状态啮合行为。在B点和F点(0.5 (1) 基于Johnson接触力模型,提出了一种计及时变齿侧间隙和啮合过程中能量耗散的渐开线内啮合直齿轮传动系统动态啮合力计算模型,考虑齿面摩擦、齿隙和综合传动误差的情况下,建立内啮合齿轮系统的五种不同的啮合状态及其对应的边界条件,推导考虑齿轮系统5态啮合行为以及时变齿隙的无量纲归一化非线性动力学模型。并克服传统啮合力模型的缺点,提出一个新型动态啮合力计算方式并代入上述动力学方程。 (2) 通过构造5种Poincaré映射,研究了在5种啮合行为下的相轨迹和动态啮合力演化规律,发现当啮合频率ω=0.3时,系统表现为稳定的周期运动。随着啮合频率增加,分岔、混沌运动相继发生。啮合频率的变化对齿轮系统的稳定性及啮合力的影响较大。此外,分岔和混沌可改变多态啮合行为的类型和啮合力方向上的突变。 (3) 啮合频率、负载等系统参数对五态啮合行为有很大影响。随着参数的不断变化,逐渐出现单、双齿齿面啮合以及单、双齿齿背啮合,啮合行为逐渐变得复杂。合理地选择啮合频率,可以避免轮齿冲击行为,以改善其动态性能和应用的可靠性。本文也为进一步研究内啮合齿轮系统的动力学特性分析奠定了基础。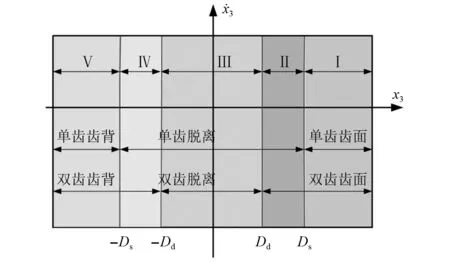
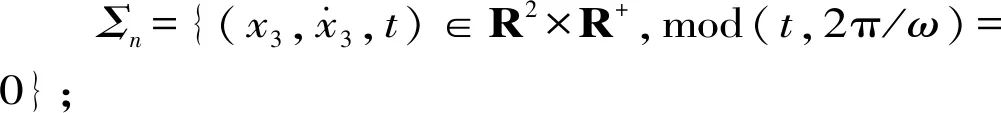
4 结 论

