面向差分隐私保护的自适应谱聚类优化新算法

金亦乔 章永祺 王 博 王鑫轲 李昭祥*

1(上海师范大学数理学院 上海 200234)

2(上海师范大学信息与机电工程学院 上海 200234)

0 引 言

近年来,大数据是互联网时代应运而生的信息技术产物,其背后所蕴含的商业价值正是网络安全问题日趋严峻的主要因素,这使得防止用户隐私信息泄露的隐私保护技术应运而生。聚类分析是数据挖掘和机器学习领域常用手段,但在聚类过程中依然存在着不可忽视的隐私泄露等安全隐患,如何在聚类过程中维持数据隐私安全和聚类可用性的平衡愈发成为近年来的研究热点之一。

由Samarati等[1]提出的传统隐私保护技术k-anonymity模型,要求数据表中的每一条记录至少与其他k-1条记录在准标识符QID上完全一致来达到隐私保护的目的,但当查询结果中所有返回值拥有同一个敏感属性值时,攻击者就可以轻易获得隐私信息[2],尤其是当今大数据平台的数据开放性,合成攻击和背景知识攻击的安全问题日渐不容小觑。基于此,l-diversity[3]、t-closeness[4]等隐私保护技术应运而生,但仍然不能完全解决该问题。

Dwork[5]2006年第一次提出了差分隐私保护模型的概念。其原理与传统隐私保护算法大相径庭,从统计分析的角度提供理论上的量化边界来约束敏感信息的泄露[6],通过为数据添加Laplace噪声干扰的方式,将确定的输出结果以概率的方式呈现出来从而达到保护隐私的目的,使得攻击者无法通过观察查询结果来获取准确的用户信息,由此引发了国内外十几年来的差分隐私保护热潮。Dwork等[7]基于Blum等[8]关于差分隐私保护和k-means结合的思想,进一步得出DPk-means算法中查询函数和查询序列敏感度的计算方法。李杨等[9]以传统DPk-means算法初始簇中心点选取的随机性为出发点提出了IDP k-means算法,在聚类可用性上取得了更好的效果;吴伟民等[10]在基于密度的聚类方法中提出了DP-DBScan聚类算法,解决了对不同规模和不同维度的数据集的有效处理;郑孝遥等[11]根据传统的聚类算法可能存在的隐私风险,以保护数据彼此间的相似度为出发点,在相似性矩阵中加上满足Lapace分布的随机噪声,切实可行地提出了一种基于差分隐私保护的谱聚类算法(简称DP-SC),改善了传统差分隐私保护处理高维稀疏数据的局限性和不理想聚类效果,但对最优聚类簇数、初始点选择的盲目性、离群点高度敏感和聚类效率、聚类可用性不理想等弊端没有开展进一步处理。

目前,面向差分隐私保护的谱聚类算法研究并不多。因此,本文针对传统差分隐私保护的谱聚类算法(DP-SC)存在的不足,提出一种基于差分隐私保护的自适应谱聚类优化新算法(IDP-SC)。仿真实验结果表明,与DP-SC算法相比较,IDP-SC算法在添加多处优化处理的情况下能保持差分隐私的安全性并有效改善聚类效率和提高聚类可用性。

1 相关工作

1.1 差分隐私保护

定义1[12]假设两个相邻数据集H与H′,它们至多只有一个元组有差异,Range(A)表示一个随机算法A的取值范围,Pr(E)表示事件E的披露风险。若随机算法A能够提供ε-差分隐私保护,则对于数据集的所有输出结果S,均满足:

Pr[A(H)∈S]≤exp(ε)×Pr[A(H′)∈S]

(1)

式中:披露风险取决于随机算法A;ε表示隐私保护参数(隐私预算),ε越小,隐私保护水平越高,但数据可用性越低,当ε=0时,随机函数A对H和H′输出结果的概率分布是完全一致的。

定义2[12]对于查询函数G:H→Rh的敏感度定义如下:

(2)

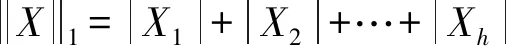
定义3[13]假设尺度参数b=ΔG/ε,则Laplace噪声函数为:

Laplace(b)=exp(-|x|/b)

(3)

概率密度函数为:

f(x|b)=exp(-x/b)/(2b)

(4)

累积分布函数为:

F(x)=0.5×[1+sgn(x)×(1-exp(-|x|/b))]

(5)

定义4[13](ε-差分隐私保护)假设数据集为H,查询函数为G,查询函数返回的结果是G(H),尺度参数b=ΔG/ε,在G(H)上添加合适Laplace随机噪声以实现保护隐私的目的,则函数T的响应值为:

T(H)=G(H)+Laplace(b)

(6)

满足ε-差分隐私保护。

1.2 差分隐私保护的谱聚类算法

谱聚类算法的原理是基于图论的思想方法[10],将数据集中的所有数据视作空间中的数据点,点与点之间的连线就构成了边,用相似度(权重)来衡量两点之间的距离,对数据点构成的图进行切图,再根据数据的Laplace矩阵的特征向量进行聚类。因此,在谱聚类算法中实现数据隐私安全的保护关键就在于样本数据集中各数据之间的相似性关系[11]。满足ε-差分隐私保护的谱聚类算法(DP-SC)的主要步骤如下:

输入:数据集data1。

输出:标签label。

Step1定义聚类种类k,根据给定的label计算出k的值。

Step2初始化k_near=10和σ=0.9,根据KNN和高斯核函数的距离公式计算各个数据间的权重值nij。

Step3为邻接矩阵N添加噪声得到加噪邻接矩阵N′。

Step4根据加噪后的邻接矩阵N′得到度矩阵K,求出Laplace矩阵L=K1/2NK1/2。

Step5求Laplace矩阵L的前k个最大的特征值和对应的特征向量。

Step6标准化特征向量,将样本数据点映射到基于一个或多个确定的降维空间中去。

Step7利用k-means聚类方法,得到聚类后的label值。

与传统的k-means聚类算法相比,基于图论的谱聚类算法能够将高维凸形的任意形状的稀疏数据进行聚类,而且不容易陷入局部最优解,适用性更强[14]。由此,谱聚类算法结合差分隐私保护的思想,在相似性矩阵中加上满足Laplace分布的随机噪声,在一定的信息损失度范围内实现了有效的聚类结果[15]。但它无法保证降维幅度和聚类簇数的选取是最优的,而且对于初始点选择的盲目性、离群点的高敏感度和聚类可用性有待改善等弊端缺乏更进一步的处理。基于此,为有效解决上述问题,在保证数据隐私的同时改善聚类效率并显著提高聚类可用性的要求下,本文提出一种面向差分隐私保护的自适应谱聚类优化新算法。

2 差分隐私保护的谱聚类算法改进

设H=[hij]是一个n×h的数据集,其中每一个数据点(每一行元组)的维度是h维,矩阵W=[wij]是稀疏邻接矩阵,矩阵D=[dij]是度矩阵,矩阵L是该数据集经过W和D计算得到的n×nLaplace矩阵,映射矩阵M是前Ke个特征值所对应的特征向量组合后得到的n×Ke矩阵。

2.1 互邻高斯核函数

高斯核函数能够利用高维向量之间的内积得出两个高维向量之间的距离,有效减少计算的复杂程度。为了得到稀疏邻接矩阵W,提出互邻高斯核函数的概念如下,实现高斯核函数和KNN算法的有机结合。

定义5(互邻高斯核函数)假设vi和vj是两个数据点,如果vi在vj的k_near领域中并且vj也在vi的k_near领域中,则权重wij=wji为vi与vj之间的距离,否则权重取值为0,其中wij为高斯核函数的计算值,k_near为KNN算法的参数[16-17]。

2.2 自适应聚类簇数

IDP-SC可以分解为如下2个阶段:

(1) 降维阶段:通过处理矩阵L的数据特征,将原始的高维数据点映射到一个低维的映射空间,即得到映射矩阵M,具体见算法1。

算法1求解降维最优簇数Ke

输入:矩阵L。

输出:降维最优簇数Ke和映射矩阵M。

Step1归一化矩阵L,计算特征值及对应的特征向量。

Step2从小到大排列这n个特征值E(1),E(2),…,E(n)。

Step3初始化特征值阈值εe=average(ΔE(i)),其中i=0,1,…,n-1。

Step4按照次序比较ΔE(i),首次满足ΔE(i)>εe时,得到降维最优簇数Ke。

Step5依次排序前Ke个特征值所对应的特征向量,得到映射矩阵M。

(2) 聚类阶段:在低维的特征空间中,对映射矩阵M的特征向量进行聚类[14],具体见算法2。

算法2求解聚类最优簇数Ks

输入:映射矩阵M。

输出:聚类最优簇数Ks。

Step1建立以聚类簇数为X和误差平方和为Y的直角坐标系。

Step2根据映射矩阵M,计算每一个X=S点对应的SSES以及相邻两点之间的斜率绝对值|Slope|。

Step3初始化斜率阈值εs=SSE1/Kmax。

Step4从大到小比较|Slope|,首次满足|Slope|<εs时,得到聚类最优簇数Ks。

定义6(降维最优簇数Ke)在降维阶段中,从小到大排列矩阵L的n个特征值E(1),E(2),…,E(n),第一次出现第Ke个次序特征值与第Ke+1个次序特征值的差距ΔE(i)=E(i+1)-E(i)大于特征值阈值εs(Epsilon Eigenvalue)的情况,即两相邻次序特征值差的绝对值首次满足ΔE(i)>εe时,降维最优簇数的取值Ke。

事实上,(低维映射空间)映射矩阵M的列向量就是这前Ke个特征值所对应的特征向量。

定义7(聚类最优簇数Ks)在聚类阶段中,根据映射矩阵M中的降维数据,建立以聚类簇数为X轴和误差平方和为Y轴的直角坐标系,记录下X轴相邻两点之间的斜率Slopes。第一次出现Slopes的绝对值小于斜率阈值εs(Epsilon Slope)的情况,即相邻两点斜率的绝对值首次满足时|Slopes|<εs,聚类最优簇数的取值为Ks。

其中,Ke、Ks为正整数且2≤Ke,Ks≤Kmax,为保准IDP-SC的降维幅度和聚类有效性,一般取Kmax=8。

定义8(Sum of Squared Errors,SSE)其是K-means聚类算法中最常用的评价指标。它是所有数据点到其所属簇质心的距离平方和。SSE越小,表示聚类结果越好。计算公式如下:

(7)

式中:K为聚类数;mi为第i个聚类中心;j是第i类簇的第i个数据点。

定义9对于面向差分隐私保护的谱聚类算法的自适应最优聚类簇数AOC的定义如下:

AOC=min{Ke,Ks}

(8)

式中:Ke是降维阶段的降维最优簇数;Ks是聚类阶段的聚类最优簇数。

2.3 中间信息向量

TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)法是一种有效的多指标评价方法,能够充分利用原始数据的内在特征,其结果可以精确反映数据之间的差距,是一种逼近于理想解的排序法[18]。本文利用TOPSIS法的思想计算中间信息向量的目的是为了有效处理谱聚类算法中聚类阶段第一个初始簇中心选择的盲目性,即选取各数据特征的信息最为折中且最有价值的VII以得到更优的第一个初始簇中心来优化算法。

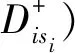
(9)

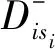
(10)

式中:wij为邻接矩阵W中第i行第j列的权重值。

定义11(中间信息向量VII)将数据集H中n个h维的向量根据数据特征的不同分别进行排名,根据这个数据特征的排名综合评分,分数处于排名中间项的那个向量就叫做中间信息向量。

由于VII是数据集H中各个数据特征综合排名的中间项,因此它具有良好的中间性(Intermediateness),在代表全体向量各个维度上的信息是最有价值的唯一向量;它也具有低敏感度(Low-Sensitivity),即对任一数据特征的离群点敏感度较低。

2.4 差分隐私保护的自适应谱聚类优化新算法

算法3IDP-SC算法

输入:数据集H。

输出:IDP-SC蔟类CIDP={C1,C2,…,CAOC}。

Step1根据数据集H,运用互邻高斯核函数的概念得到稀疏邻接矩阵W。

Step2为稀疏邻接矩阵添加Laplace随机噪声得到加噪邻接矩阵W′,并计算求得度矩阵D。

Step3求出标准化Laplace矩阵L=D1/2W′D1/2。

Step4根据Laplace矩阵L,采用算法1和算法2依次求得降维最优簇数Ke、映射矩阵M和聚类最优簇数Ks,结合式(8)得到IDP-SC的自适应最优聚类簇数AOC。

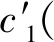
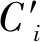
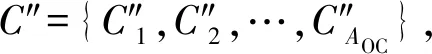
Step8后续迭代采用传统k-means++算法,直至算法收敛或蔟中心不再变动,输出最优蔟类CIDP={C1,C2,…,CAOC}。

3 实验与结果分析

3.1 实验环境与数据集

本文涉及的算法均使用Visual Studio 2019集成开发环境的Python 3.8语言仿真实现。实验环境为Windows 10 x64,CPU 2.30 GHz,内存16.0 GB。算法所涉及的数据集均来自于:UCI Knowledge Discovery Archive database。

各数据集信息如表1所示。

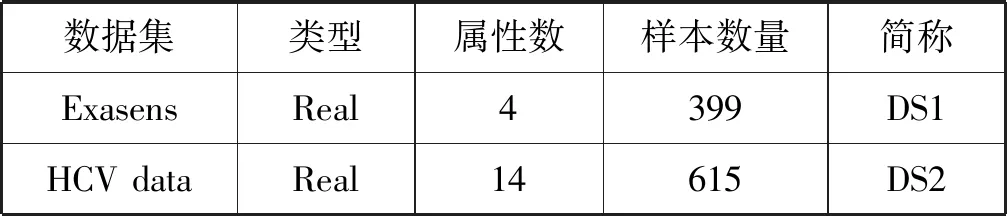
表1 UCI数据集信息

首先对数据集DS1和DS2进行归一化处理[19],使其所有数据点的各个属性值都映射至区间[0,1]之间,消除量纲并提升模型精度。

(11)

式中:maxX和minX分别代表数据集中属性X的最大值和最小值;x表示数据集中的数据点;x′表示经过归一化处理之后的数据点。

3.2 实验评价指标

差分隐私数据挖掘类算法取决于差分隐私保护下的保护强度和数据挖掘聚类算法下的聚类效果。隐私保护程度可以通过隐私预算ε来评估,其值越小,添加的Laplace随机噪声越大,隐私保护水平越高,但聚类可用性越低;聚类效果可以从两方面进行评价,即聚类算法的聚类效率和聚类可用性。

3.2.1聚类效率

差分隐私保护模型下的聚类效率可以采用聚类过程中算法收敛或簇中心不再变动时的迭代次数来评价,同时它也是衡量聚类算法初始簇中心选取合理性的有效指标。迭代次数越小表示初始簇中心点的选择越合理,算法聚类效率越高。

3.2.2聚类可用性

差分隐私保护模型下的聚类可用性可以使用兰德系数RI指标和修正兰德系数ARI指标评价。对于数据集H,假设用C表示实际类别信息,K表示最终聚类结果,a表示C和K中属于同一类别的元素数量,b表示C和K中属于不同类别的元素数量,则RI指标[20]如式(12)所示。

(12)

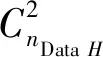
但在仿真实验中,算法实现计算得到的RI值普遍偏高导致区分度不明显,由此ARI指标[20]被提出,如式(13)所示。

(13)

式中:E(RI)表示RI的数学期望,ARI取值范围[0,1],ARI值越大表示聚类结果和真实情况越吻合,聚类可用性越好。

3.3 结果分析

对数据集DS1和DS2分别采用DP-SC算法和IDP-SC算法进行对比实验,在评价聚类效率指标时将隐私预算ε的值逐步从0.1调至2.0,在评价聚类可用性指标时将隐私预算ε的值逐步从0.1调至1.0。为了避免算法随机性而导致的实验结果存在偶然性,根据每个隐私预算ε值,对DS1和DS2分别采用DP-SC和IDP-SC算法聚类20次,并将其评价指标结果的平均值作为最终的实验结果。

在数据集DS1和DS2上运行的聚类效率评价结果分别如图1和图2所示。

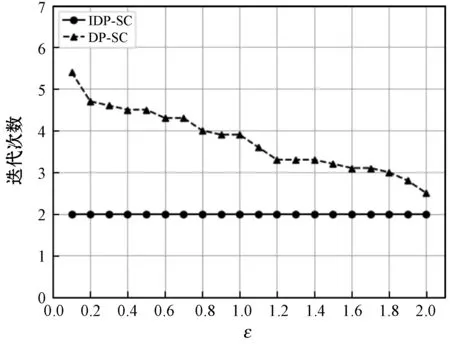
图1 数据集DS1的聚类效率评价结果

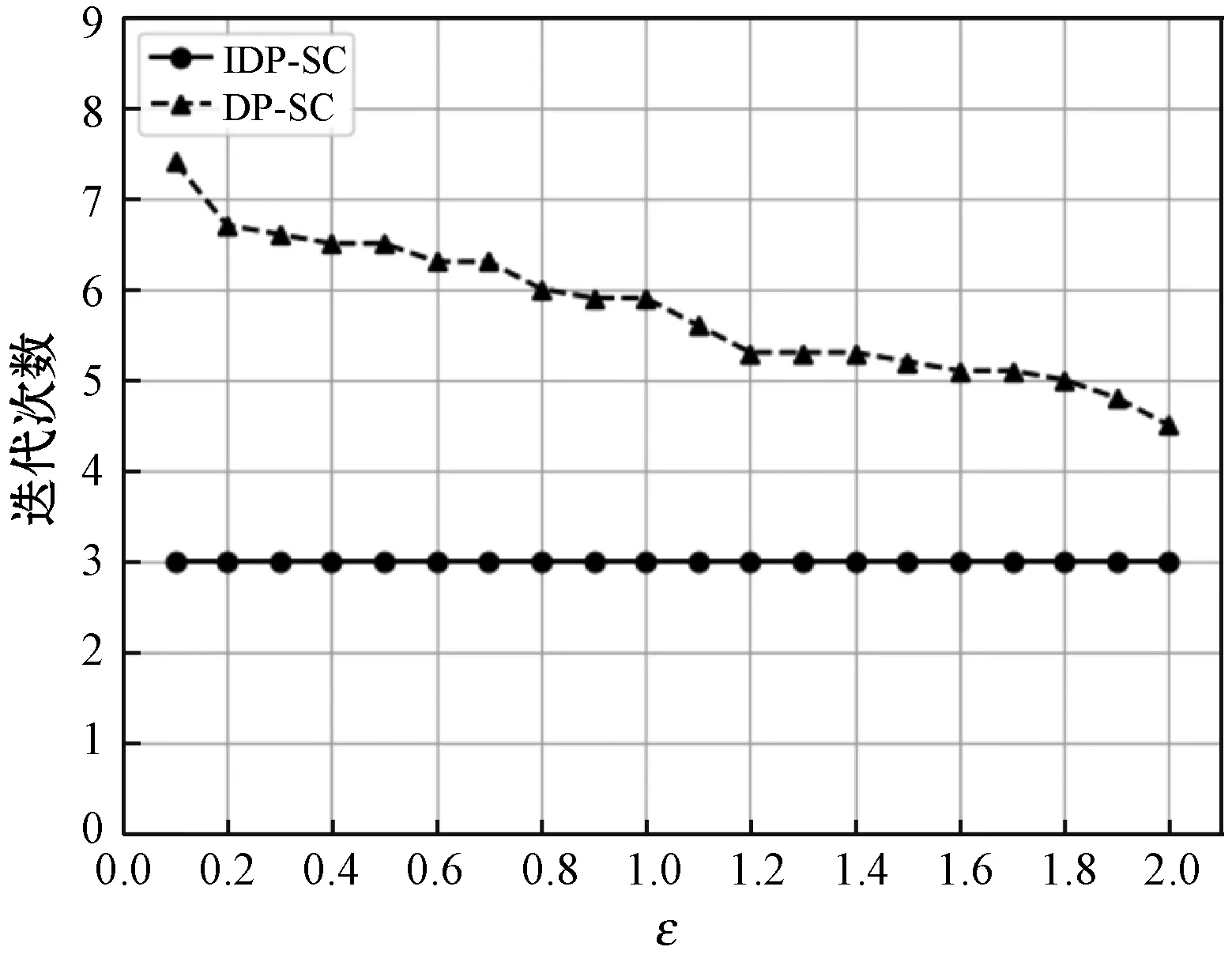
图2 数据集DS2的聚类效率评价结果

结合图1和图2可以发现,对于数据集DS1和DS2的实验结果来说,在同一隐私预算ε下,本文提出的IDP-SC算法与传统的DP-SC算法相比,IDP-SC算法的平均迭代次数明显小于DP-SC算法且具有稳健性,意味着IDP-SC采用中间信息向量的概念挑选第一个初始簇中心的方法可以有效提高聚类效率,并且随着隐私预算ε的增加,DP-SC算法的平均迭代次数逐渐减少,聚类效率越来越高,趋近于IDP-SC的平均迭代次数。这说明新算法在保证数据隐私的同时可以有效提高聚类效率。值得一提的是,对于高维数据集,新算法在聚类效率上的改进效果尤其显著。

在数据集DS1和DS2上运行的聚类可用性评价结果分别如图3和图4所示。

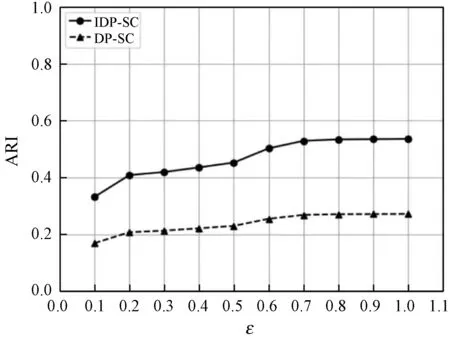
图3 数据集DS1的聚类可用性评价结果

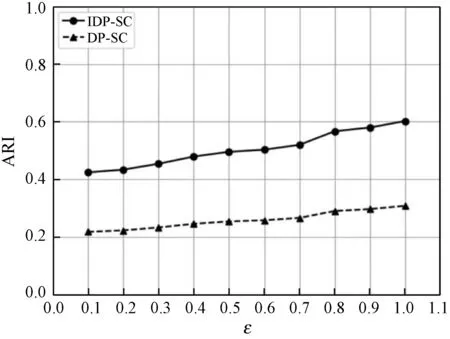
图4 数据集DS2的聚类可用性评价结果

结合图3和图4可以发现,对于数据集DS1和DS2的实验结果来说,在同一隐私预算ε下,本文提出的IDP-SC算法与传统的DP-SC算法相比,显然具有更高的ARI评价结果,这说明新算法在保证数据隐私的同时可以显著提高聚类可用性。不难看出,对于高低纬数据集,本文算法在聚类可用性上的改进效果都比较显著。

图3和图4分别展示的是在DS1和DS2数据集上,针对不同的隐私预算ε值分别调用DP-SC算法和IDP-SC算法进行聚类20次后得到的ARI的平均值折线图。可以看出,IDP-SC算法的聚类可用性明显要高于DP-SC,同时随着隐私预算的增大,添加的噪声量减小,使得聚类可用性也越高。不难得出,对于高低纬数据集,本文算法在聚类可用性上的改进效果都比较显著。

4 结 语

本文针对传统的差分隐私保护的谱聚类算法(DP-SC),提出基于差分隐私保护的自适应谱聚类优化新算法(IDP-SC),有效解决了降维幅度和聚类簇数的不确定性、初始簇中心选取的随机性和离群点高敏感度等问题而可能导致出现聚类效果不理想的情况。

首先本文算法结合KNN思想和高斯核函数的概念提出互邻高斯核函数,有效处理了高维大样本场合数据集的计算压力;通过分析高维数据点的数据特征与聚类簇数的关系自适应地得到IDP-SC的最优聚类簇数,再利用TOPSIS思想引入中间信息向量和中间性的概念处理聚类阶段第一个初始簇中心选取的随机性,最后根据多维高斯分布离群点检验后的结果采用插补法解决离群点问题。仿真实验结果表明,IDP-SC在高维大样本场合数据集下,能够在保证差分隐私安全性的同时改善聚类效率并显著提高聚类可用性,切实把握住数据隐私和聚类效果两者的平衡。在以后的研究中,将继续深入研究如何有效减少算法的复杂程度,在保证差分隐私技术的安全性下进一步提高运行效率和聚类可用性,特别是如何显著提高维数据集的聚类可用性。