基于支持向量机的高速铁路曲线状态评价方法

郝丽楠 刘金朝 李忠艳

1.华北电力大学 数理学院， 北京 102206； 2.中国铁道科学研究院集团有限公司 基础设施检测研究所， 北京 100081

高速铁路运行速度快、行车密度高、车辆线路之间作用力大，容易导致线路线形不同程度地偏离理想状态［1］。曲线地段病害较多，是线路薄弱环节及质量优劣重要控制区段，对曲线状态进行科学评价，智能化快速检测曲线轨道状态是掌握线路技术状态的重要手段［2］。

部分学者对高速铁路轨道状态进行了相关研究，余宁等［3］针对现役轨道检测系统中曲线特征点检测算法参数难以适应实际线路中曲线半径范围较大，以及由于参数设置不当导致检测的曲线特征点位置与实际位置偏差较大的问题，结合机器学习算法，提出了一种基于卷积神经网络的曲线特征点检测算法。严录录等［4］提出了基于轨道检查车动态正矢的曲线状态评价方法，提高了正矢检查效率。但尚没有一套完整的基于车辆动态响应智能化快速检测曲线状态的方法。

本文应用支持向量机（Support Vector Machine，SVM）模型，提出模型最优参数搜索方法，进而提出一套基于车体横向加速度的曲线状态综合评价方法，并对高速铁路曲线状态进行检测。

1 基于SVM的曲线状态分类模型

1.1 完全经验模态分解与自适应噪声抑制算法（CEEMDAN）简介

CEEMDAN（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise）算法［5］主要思想是在分解过程中加入特定频带内的白噪声。对于待处理信号X[t]，CEEMDAN 使用相同的经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）算法先计算第一模态C1（t），再计算第一残差r1(t) =X[t]-C1(t)。然后，计算给定噪声的集合r1(t)的不同实现上的EMD 模式，通过平均得到第二模态C2(t)，随后计算r2(t) =r1(t) -C2(t)，重复这一步骤直到残差余量不能被分解时停止。

1.2 支持向量机（SVM）简介

SVM［6］的核心思想是构造一个超平面将两种状态类型的样本分开并使超平面两侧的样本到该平面的距离最大。这样才能使分隔具有更高的可信度，对新样本也具有很好的分类预测能力。

对于线性可分性问题，用于分类的超平面为

式中：X为输入向量；W为权值向量；b为偏移量。

在SVM 模型中，多个样本点分布在分类超平面周围，称为支持向量。分类超平面与超平面两侧的支持向量之间的距离之和称为边距。根据输入数据是否线性，可将最优分类超平面的解分为两种情况。当训练集中的样本线性可分时，求解可以转化为一个二次凸优化问题，当样本线性不可分时，对应的二次凸优化问题需要引入惩罚系数和松弛变量。当输入模型的数据为非线性时，需要引入核函数K(x∙xi)，将样本x映射到高维空间，并对样本进行线性分割。

1.3 支持向量机模型参数选择方法

SVM 模型参数是影响其性能的重要因素，本文在穷举法基础上提出可程序化最优参数搜索方法。

1）量级选择。根据经验对其惩罚系数和核函数固有参数进行初始化量级（i）赋值，形成量级序列{10-i，101-i，…，10i-1，10i}，然后通过试验测试结果选择量级。

2）等距选择。根据所选量级，在其左右两侧分别以等距的形式排列若干个参数值。若已选择量级为i，可设置{ 10i-1，4 × 10i-1，7 × 10i-1，10i，4 × 10i，7 × 10i，10i+1}这样的等距参数序列，然后通过试验测试结果选择最优参数的大致位置。

3）两侧折中逼近。根据等距选择出最优参数的大致位置，在其左右分别进行折中以找到最优参数。如果等距选择出的最优参数为4.0 × 10i，则可设置{1.0 × 10i， 2.5 × 10i， 4.0 × 10i， 5.5 × 10i， 7.0 × 10i}这样的参数序列，然后通过试验测试结果以逼近最优参数，循环两侧折中逼近，直至模型不再提升。

支持向量机模型参数选择方法避免了传统穷举法搜索参数时较大程度受到操作者经验的影响，泛化能力强，适用于支持向量机惩罚因子和核函数固有参数搜索，且可程序化。

1.4 曲线状态评价模型

基于车体横向加速度数据，建立基于SVM 的曲线状态评价模型，主要包含里程信息提取、特征提取、模型训练、曲线状态分类等步骤。

1）对车体横向加速度数据集作傅里叶变换，提取数据趋势，并用单一阈值法提取曲线区间里程信息。

2）根据曲线区间里程信息划分样本，对车体横向加速度数据集做CEEMDAN 分解，获取曲线区间内车体横向加速度高频分量。

3）根据曲线区间内车体横向加速度高频分量，提取样本数据特征［7-8］。

4）训练SVM 模型，寻找最优参数，实现两类曲线状态的分类。

2 曲线区间里程信息提取

本文采用车体横向加速度数据提取曲线区间里程信息，并进行曲线状态评价。图1 为某高速铁路线路前50 km车体横向加速度原始波形。

图1 车体横向加速度原始数据

由图1 可知：车体横向加速度数据受到高速铁路轨道状态及白噪声影响，波形复杂，不易于提取曲线区间里程信息。

考虑到数据特征、定位精度以及应用需求，本文采用傅里叶变换和逆傅里叶变换方法对原始数据预处理以提取数据趋势项，提取频率为0 ～ 0.002 Hz 的信息，见图2。其中“△”表示曲线区间起始里程，“○”表示曲线区间终止里程。可知，该方法较好地提取了车体横向加速度数据的趋势。

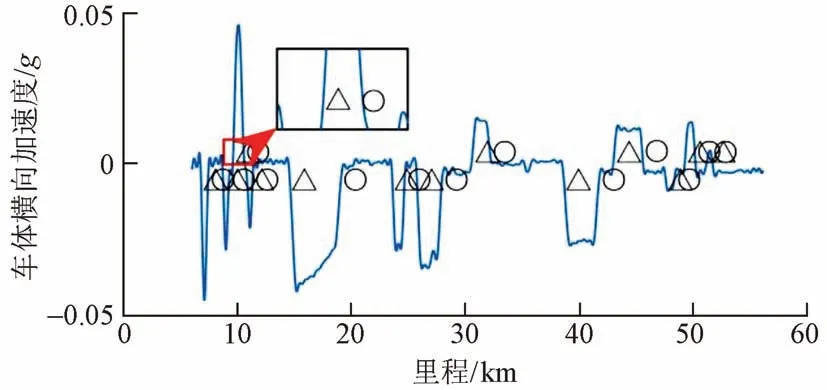
图2 基于车体横向加速度曲线里程信息

实际上，高速列车在直线区段行驶时，车体横向加速度理论上应在0附近受轨道平顺度影响和白噪声干扰呈现微小波动，而在曲线区间行驶时，车体横向加速度由于受到离心力作用波形呈现剧烈变化。基于上述数据特征，在傅里叶分析基础上，运用单一阈值法提取曲线区间里程信息。加速度传感器在该线路前50 km 检测出13段曲线。全线共检测出129段曲线，考虑里程信息存在一定偏差，本文对单一阈值法提取的各个曲线区间向前向后各延伸200 m，以保证曲线区间位于所提取的里程之间。

3 特征提取

3.1 基于CEEMDAN算法的去趋势项

本文将对各曲线的车体横向加速度数据依次做CEEMDAN 分解，迭代次数为500，加入了0.002 正负高斯白噪声。以K25 + 506.25—K28 + 100.50 曲线区间为例，通过CEEMDAN 分解得到从高频到低频依次排列的12个分量，见图3。图4为相应分量的功率谱，可知分量1—分量8 为含噪分量，分量9—分量11 和残差为该信号的趋势项。

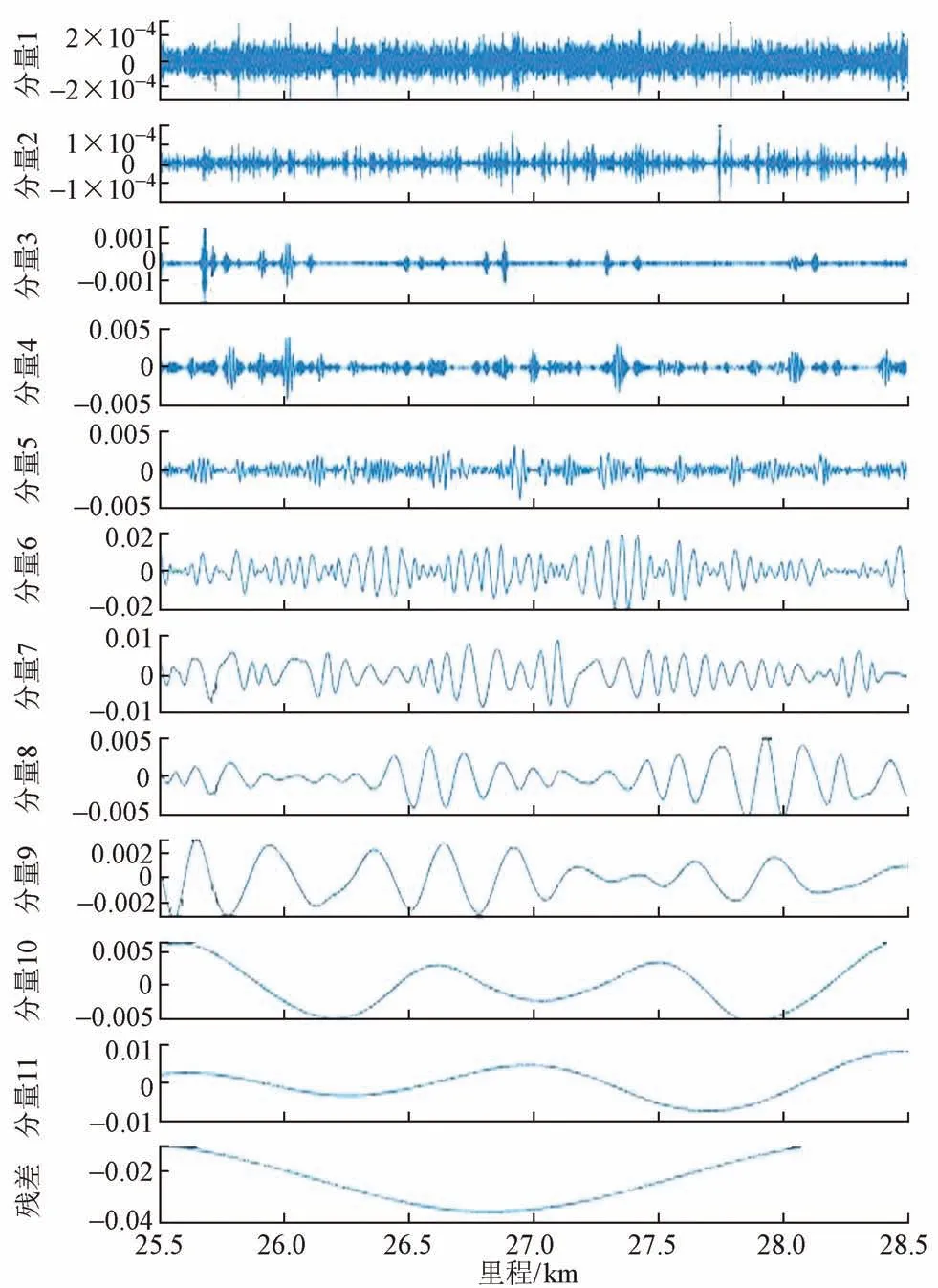
图3 曲线CEEMDAN分解各分量

由于CEEMDAN 分解具有完备性，因此以分量4—分量8 的高频分量作为线路高频分量进行分析评价，见图5。可知，该方法有效滤除了白噪声干扰，并较好地分离了趋势项和高频分量，这为曲线状态特征提取奠定了基础。

3.2 基于高频分量的特征提取

基于高频分量，依次提取了各曲线的峰值、峰峰值和有效值。其中，峰值指变化的车体横向加速度数据的最大瞬间值，本文所取峰值为峰值的绝对值；峰峰值指车体横向加速度数据最大值和最小值之间的差值，描述信号值变化范围的大小；有效值指车体横向加速度数据的均方根值，描述该曲线信号值的能量大小，反映综合情况［9］。

本文共提取了全线129 段曲线区间的特征向量数据，见表1。其中，峰值的最大值为0.086、最小值为0.008，峰峰值的最大值为0.151、最小值为0.014，有效值的最大值为0.013、最小值为0.002。峰值、峰峰值和有效值的数值越大，曲线状态越差。

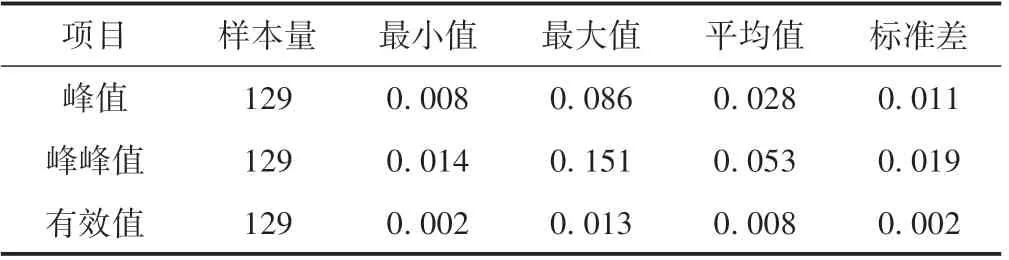
表1 特征向量数据

4 试验验证

曲线状态分为状态良好和状态不良两类，两种状态下高频车体横向加速度信号数据集的波形、特征见图6 和表2。曲线状态正常的高频车体横向加速度信号数据集的波形具有较小的振幅和较小的特征值，而曲线状态异常的波形具有较大的振幅和较大的特征值，说明可能存在病害，威胁列车运行安全。为了快速检测出异常状态曲线，选择一个曲线区间的车体横向加速度信号数据集作为样本，使用前述方法实现两种状态的分类。

表2 两种状态本体横向加速度高频分量特征对比

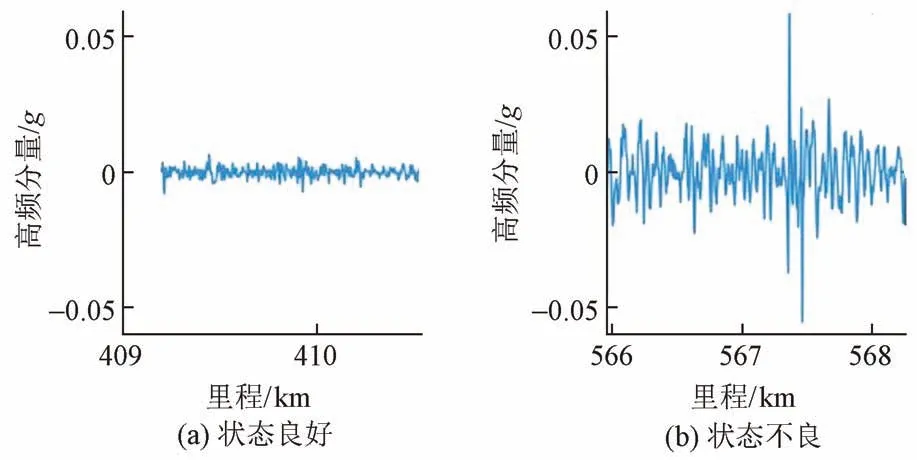
图6 两种状态车体横向加速度高频分量波形对比

将前文得到的样本特征数据输入支持向量机训练与预测，取该线路前60 条曲线作为训练样本，剩余的69个曲线作为测试样本。在测试样本中，曲线状态良好的样本为56 个，曲线状态不良的样本为13 个。本试验使用的样本集是不平衡的，状态良好和状态不良的样本量之比约为4∶1，无约束的SVM 训练会使分类超平面偏向状态不良，因此通过改变样本类别的权重来增加模型对少量样本重视程度，以防止出现过拟合现象。

通过试验，该模型选用线性超平面，采用支持向量机模型参数方法搜索最优参数。最终得到的模型参数惩罚系数为0.5，核函数系数为0.08。

选择准确率（A）、精确率（P）、召回率（R）及F1分数四个指标评价基于SVM 曲线状态预测模型的分类效果。各指标定义为

式中：QTP为正确分类的正样本数；QTN为正确分类的负样本数；QFP为错误分类的负样本数；QFN为错误分类的正样本数。

基于SVM 的曲线状态预测模型的分类效果见表3。可见，准确率为98.55%，精确率为98.58%，召回率为98.55%，F1分数为98.53%，表明基于SVM 的曲线状态预测模型是有效可行的。

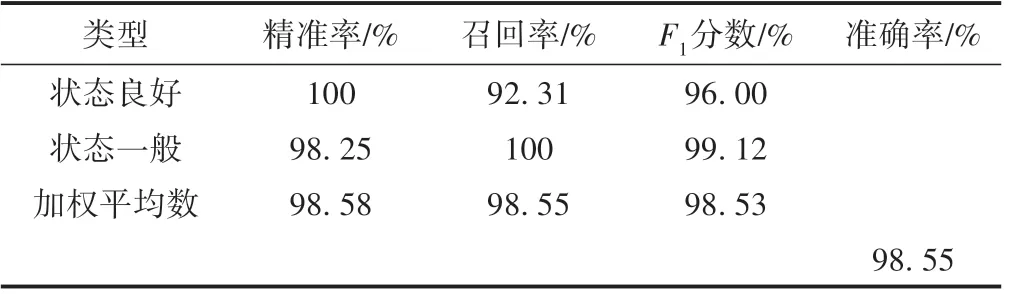
表3 模型分类效果

5 结论

本文提出一套基于车体横向加速度数据集的曲线状态综合评价方法，并结合SVM 实现对高速铁路曲线状态的评价与检测。主要方法与结论如下：

1）运用傅里叶分析对车体横向加速度数据集预处理提取数据趋势项，在此基础上运用单一阈值法提取了曲线的里程信息，全线共提取129段曲线。

2）基于车体横向加速度数据特点，对各曲线数据依次实施CEEMDAN分解；针对高频分量，依次提取各曲线区间高频分量的峰值、峰峰值和有效值作为特征向量。

3）为达到曲线状态检测分类的目的，选用线性超平面，并采用支持向量机模型参数方法搜索最优参数方法进行最优参数的选择，实验表明，模型的准确率为98.55%，精确率为98.58%，召回率为98.55%，F1分数为98.53%，基于SVM 曲线状态预测模型是有效可行的。