求解时变非线性方程的离散时间ZNN算法

刘巧莲，孙肖丽，孙 敏

(枣庄学院 a.信息科学与工程学院；b.数学与统计学院，山东 枣庄 277160)

0 引言

方程是数学学科一个重要研究对象，其可以描述科学领域的许多问题，如测量学中的勾股定理、量子力学中的薛定谔方程、金融学中的布莱克-斯科尔斯期权定价公式等。另外，还有很多问题可以通过等价变形转化成方程形式，如可微约束优化问题的一阶必要条件是一个变分不等式，而该不等式可以通过投影算子转化成一个非线性方程[1]。因此，学者们对各类方程的解析解与数值解进行了深入的研究，与方程相关的研究成果浩如烟海。

本文考虑一类代数方程，即时变非线性方程。与微分方程类似，时变非线性方程中也含有时间参数t。二者的不同之处在于，微分方程描述的是一个变量随时间变化所满足的规律或定律，比如描述放射性元素镭衰变的微分方程

M′(t)=-KM(t)，K>0，

其中M(t)表示时刻t镭的留存量。该方程是“镭的衰变速度与留存量成正比”这一规律的数学描述或建模。而时变非线性方程(time-varying nonlinear equation，TVNE)具有如下数学结构：求x(t)∈Rn满足

F(x，t)=0，t∈[0，tf]，

其中映射F：Rn+1→Rn关于变量x，t可导，tf>0表示所研究对象的最终时间节点。在每个固定时刻，TVNE退化成一个代数方程，因此可以将TVNE看成一个代数方程流。TVNE可以描述很多的实际问题，比如在冗余机械臂路径规划中，在一个规划周期内，希望每个时刻点机械臂末端执行器与目标路径都是一致的，因而可以将该问题描述成一个时变非线性方程[2]。

零化神经网络(zeroing neural network，ZNN)是解决各种时变问题的基准求解器[3-4]，其可分为两类：(1)连续时间ZNN，往往是一个微分方程；(2)离散时间ZNN，往往是一个差分方程。相比于连续时间ZNN，离散时间ZNN在结构上更简单，操作更方便，应用更灵活。目前，对离散时间ZNN的研究主要是基于一步前向差商(分)的显式线性(单)多步长方法，如Euler格式、Adams格式等。2019年，Sun等[5-6]研究了离散时间ZNN，先后提出了一种通用的两步到六步的离散时间ZNN。比如，文献[6]借助于Routh稳定性分析理论，给出了一般六步离散连续时间ZNN，并给出了精确描述其自由参数值的范围；借助于Jury稳定性理论，给出了步长的精确范围。传统的ZNN在无噪声环境下是有效的，然而在现实生活中噪声是一种常见的现象，信息采集系统采集的数据往往受到各种噪声的污染。JIN等[7]设计了一个带积分项的ZNN公式，用于解决具有加性常数噪声的实时变矩阵求逆问题。ZNN公式可以看作是一种比例积分微分控制律，即控制理论中的PID控制。与以往经典的零化神经网络(实际上是PD控制)相比，该模型对噪声的敏感性大大降低，因此积分项的引入增强了系统的鲁棒性。在线性噪声和任意有界噪声下，文献[7]证明了所提ZNN的残差有上界，且上界与模型的设计参数成反比。

1 连续时间ZNN

文章将F(x，t)简记为F，类似将偏导数F1(x，t)、F2(x，t)、F11(x，t)、F12(x，t)、F22(x，t)简记为F1、F2、F11、F12、F22。

为了获取具有更高阶截断误差的算法，考虑如下的二阶微分方程：

e"(t)=-γe(t)-λe′(t)，

(1)

式中：γ>0，λ>0是设计参数。在式(1)中，令e(t)=F(x，t)，得

(2)

令x1(t)=x(t)，x2(t)=x′(t)，则得到一个新的连续时间ZNN

(3)

假设1二阶微分方程(1)中的参数γ，λ使得二次多项式s2+λs+γ=0的两个根全在左半平面。

定理1连续时间ZNN(3)产生的残量误差F(x，t)收敛于0。

证明根据上面的分析，式(3)等价于式(1)。显然式(1)可以分解成

(4)

在(4)式两端做拉普拉斯变换得

式中：εi(s)是ei(t)的象函数。对上式整理得

根据假设1，上式右端的传递函数的两个极点都位于左半平面，因此二阶系统(4)是稳定的并且终止定理成立，于是有

因此命题成立。

2 离散时间ZNN

令tk=kτ，其中τ>0是采样周期。将e(tk)简记为ek。下面利用具有二阶截断误差的中心差商来近似导数[7]

则有

将上面的中心差商代入(1)式得

整理得

(5)

H(z)=(2+λτ)z2+(-4+2γτ2)z+(2-λτ)。

(6)

γ>0，4-γτ2>0，λτ>0.

(7)

证明根据Jury稳定判据，只需要保证特征方程(6)的根全落在单位圆内即可。于是根据Jury稳定表格，只需要保证

式中：ai是(6)式中zi(i=0，1，2)的系数。对上面的不等式整理得本命题的结论。

注1满足不等式组(7)的参数是存在的，比如γ=λ=1，τ=0.1。

下面中心差商公式应用到(2)式，得到如下的离散时间ZNN

(8)

注2当F11，k≠0时，公式(8)是一个非线性差分方程，其求解难度较大。当(1)是一个时变线性方程组时，有F11，k=0，此时可以比较方便的使用式(8)。

下面利用具有四阶截断误差的中心差商来近似导数[7]

则有

将上面的中心差商代入(1)式得

整理得

(9)

H(z)=(1+λτ)z4-(16+8λτ)z3+(30-12γτ2)z2-(16-8λτ)z+(1-λτ)。

(10)

为了避免(8)式的隐式结构，再考虑利用两步前向差商来离散化(2)式。

引理1令两步前向差商

(11)

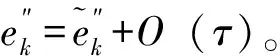
证明考虑如下的泰勒展开式

于是有

因此命题成立。

将一步前向差商与两步前向差商(11)代入连续时间ZNN(2)得

整理得

(12)

H(z)=z2+(-2+λτ)z+(1+2γτ2-λτ)。

(13)

γ>0，γτ2-λτ+2>0，λ>2γτ.

(14)

证明利用与定理2一样的证明过程可以得到本命题的结论。

注3满足式(14)的参数是存在的，比如γ=λ=1，τ=0.1。

下面将两步前向差商公式(11)应用到(2)式，得到如下的离散时间ZNN

整理可得

(15)

注4利用上面的设计思路，可以设计更多的离散时间ZNN。

注5离散时间ZNN(15)中的F11，k(xk+1-xk)2涉及张量运算，其具体的计算方法可以参考文献[9]。

3 数值实验

问题1考虑时变非线性超越方程问题

F(x，t)=2x+sinx-t，t∈[0，10].

图1 CTZNN求解问题1的结果

由图1可以看出，CTZNN比较好的解决了这个时变非线性超越方程，最终的误差稳定在10-5。

问题2考虑时变线性方程组问题

根据前面的分析，式(8)(记为DTZNN(8))可以求解这个问题，参数γ=λ=1，τ=0.01，两个初始值取为x0=[-1，0]T，x1=[-1，0.02]T，求解的结果显示在图2中，其中纵坐标表示误差，定义是

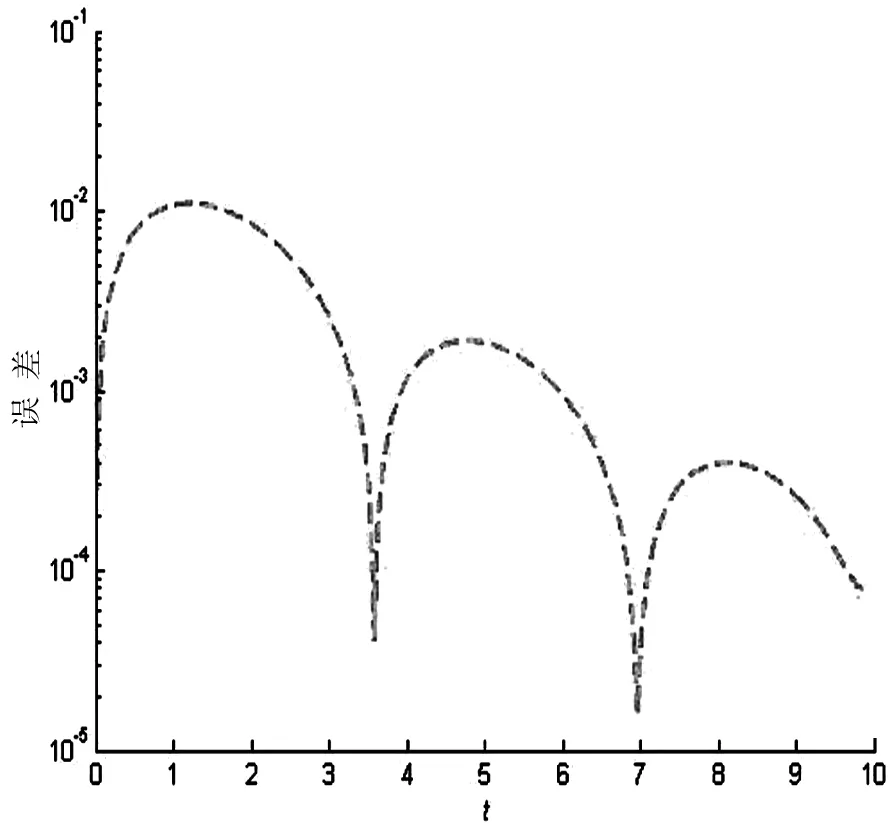
图2 DTZNN(8)求解问题2的结果

(Error)k=Fk。

由图2可以看出，DTZNN(8)比较成功的解决了这个时变线性方程组问题，在前10s内，误差一直在呈现周期性的下降趋势，第10s时的误差在10-4数量级。

问题3考虑时变非线性方程组问题

根据前面的分析，式(15)(记为DTZNN(15))可以求解这个问题，参数γ=λ=1，τ=0.01，两个初始值取为x0=[0，0]T，x1=[0.01，0.01]T，求解的结果显示在图3中。

图3 DTZNN(15)求解问题3的结果

由图3可以看出，DTZNN(15)比较成功的解决了这个时变非线性方程组问题，在前10s内，误差几乎一直在呈现下降的趋势，第10s时的误差在10-3数量级。