基于多视点和条纹的高反射表面面形测量技术

王志卓，卢荣胜

（合肥工业大学 光电工程学院，合肥 230009）

0 引言

高反射表面三维测量是工业测量的重要组成部分，且随着汽车组装、精密抛光、自由曲面加工等行业的不断发展，对于飞机尾翼、液晶显示器面板、汽车车身外壳以及挡风玻璃等大尺寸、大曲率工业零件的测量需求愈发强烈［1-4］。但由于其与漫反射物体表面光学特性存在较大差异，传统的三维测量手段［5-6］难以达到理想的效果。

现阶段，高反射表面三维形貌测量手段按照其数据获取方式不同可分为接触式测量［5-6］和非接触式测量［7-8］两大类。其中接触式测量方法虽然不受被测物表面光学性质的影响，但往往只能实现单点测量，尤其是对大尺寸三维形貌的测量，测量速度慢、耗时时间长。因此从20 世纪50 年代开始，研究人员开发出一系列非接触式表面形貌测量方法，其中光学三维测量方法由于其精度高、速度快、无接触的特点受到众多科研工作者的推崇。其中，相干法［9-10］利用被测物体表面的形貌变化调制测量光与参考光，令两者之间产生相位差，形成干涉条纹，解算干涉条纹的相位信息，进而获取物体表面三维形貌。该方法虽然测量精度高，但是量程小，仅适用于微小尺寸的测量，且测量自由曲面和结构化曲面困难。相位轮廓法［11-12］测量技术成熟，应用范围广泛。其主要由投影装置、被测物体以及CCD 相机组成，采用在被测高反面喷涂显影剂的方式，将高反射表面转化为漫反射表面。然而，喷涂的显影剂使零件表面粗糙度发生了变化并且掩盖了微小形貌，这无疑降低了精度。而相位偏折法［13-16］作为一种近年来发展起来的高反表面光学测量手段，由于其精度高、敏感性强的优点受到众多研究人员的青睐。该方法通常使用显示屏显示正弦光栅条纹，用相机采集受高反表面反射调制的变形条纹图像，通过解码获得包含被测面形貌信息的像素匹配关系，进而建立测面特征点坐标的数学关系，从而重建轮廓。XIAO Y L［13］利用相移偏折法建立像素匹配与被测面特征点法向量的数学关系，进行了基于单视点的光学反射镜表面的缺陷检测。YUAN T［14］、ZHOU T 等［15］采用相关迭代补偿算法对高反射表面面形进行了恢复。NGUYEN M［16］通过改进标定算法进一步提高了测量速度。然而，传统对相位偏折法的研究大多局限在小尺寸、小曲率测量的实验室场景下，在面对大尺寸、大曲率的工业高反表面测量场景时显得捉襟见肘。

其主要问题在于：一方面，相位偏折测量系统对结构参数的标定精度有着很高的要求，随着待测表面尺寸的增加，相机的视场与参考屏幕的尺寸也不可避免地增大，各类误差对最终标定精度的影响也会随之增加。对于单视点系统而言，由于镜面测量是一种离轴配置系统，对几何校准误差非常敏感。因此对于高精度测量需要一种高精度且鲁棒性好的标定过程，包括相机内参标定和几何标定，以精确确定屏幕、摄像机和被测表面的相对位置。虽然常规相机标定技术已经较为成熟，但用于识别屏幕和相机之间相对位置的几何校准仍在研究中。其中KUMAR R K［17］提出利用旋转矩阵的列向量与物体和镜像对应点连线所在方向向量的正交性约束，列出线性方程进行求解，每组方程需至少5 幅标定图像。但是计算的位置参数与真实值有较大误差，不利于后续的参数优化。TAKAHASHI K［18］基于正交约束从三个镜像图像中返回三个三点透视问题（Perspective-three-point Problem，P3P）的唯一解。但是若观察到参考物体小于某一尺寸，则会得到错误解。HESCH J A［19］提出的方法也是从三个镜像图像中返回三个P3P 问题的解，但只能通过重新投影误差评估后，从64 个候选解中选择一个最优解。XIN L I［20］通过镜像相机旋转矩阵之和的SVD 分解来直接估计相机旋转矩阵，并通过求解一个超定的线性方程组来计算相机平移向量，以最小化物体空间共线性误差，但是对噪声较为敏感，算法稳定性差。对此，本文使用一种改进的标定方法：首先通过多次平移液晶显示器（Liquid Crystal Display，LCD）屏幕上棋盘格图像以及改变光学平台上平面镜倾斜角获得多组棋盘格图像，利用张正友标定法［21］获得镜像相机内参与外参；其次利用文献［17］中提出的基于棋盘格图像间的正交性约束，来确定LCD 屏幕到真实相机的外部参数；最后，针对LCD 屏幕上棋盘格靶点的共平面性添加约束，利用列文伯格-马尔夸特（Levenberg-marquardt，LM）优化方法获得真实相机与LCD 屏幕之间外部参数的最优解。

另一方面，由于被测高反表面每一点的法线方向不同，反射方向也不相同，传统的偏折法测量系统［13-16］很难在一个位置捕捉到受待测物体调制的整体反射光线，尤其对大尺寸、大曲率高反表面进行测量时由于存在投影编码盲点或视觉盲区，导致测量系统无法一次获得大范围的测量结果，从而降低了测量效率。一些研究利用相机间较大的重叠视场，并通过点云配准，也可以基于以上方法达到多视点的效果，但是通过重叠视场扩大的重建范围有限，且拼接过程耗费时间［22］。TARINI M［23］通过迭代估计某一点的法线和该法线附近点的深度来恢复曲面特征点的绝对坐标，但是需要给定初始深度和法向量。LIU M［24］则提出一种通过投影单幅棋盘格图像进行镜面重建的方法，建立参考平面棋盘格靶点三维坐标与棋盘格靶点二维像素坐标的反射对应，参数化镜面深度，利用多项式拟合镜面，迭代估计镜面深度。但是受棋盘格靶点疏密程度限制，无法得到完整连续的点云。本文方法与文献［23-24］相关，利用相移条纹，在参考平面位姿已知的情况下，通过相位解包裹建立归一化像平面二维特征点、参考平面三维特征点以及光亮表面反射点之间的密集反射对应，再通过将密集折反射对应关系建模为关于被测面深度的二次多项式，将深度信息作为方程组的解求出，获得被测面相对于相机的绝对位置坐标初值，最后利用反投影模型建立代价函数并使用LM 算法对其进行约束，获得精确结果。并通过设置相机阵列，同时从多角度对被侧面进行基于绝对坐标的重建，可以有效地在保证局部测量准确度的同时，通过坐标系统一，更快地实现对大尺寸、大曲率高反射面的精确测量。

要组成多视点系统，并统一所有视点的坐标系，还需完成全局标定。通常工业上大部分相机全局标定依赖于相机之间具有较大的公共视场，并通过在重叠视场放置靶标对多相机之间的外参系数进行计算［25］。然而这就制约了系统的整体测量范围，并限制了多视点系统的灵活性。并且相机的焦点由于镜面性质在被测面所成的虚像上而不在被测面上，这也为放置靶标带来了不便。也有学者［26］借助经纬仪等高精度设备构建全局坐标系，确定相机与高精密设备之间的位置关系实现全局标定。这种方法测量精度高，但是高精度设备价格昂贵且操作复杂。文中，由于在各视点进行几何标定时，各相机均分别通过镜子间接观察到唯一的参考平面，并采集图像，因而通过调整镜子角度，并保持参考平面静止，即可利用参考平面的唯一性，在完成各视点几何标定之后，获得多视点系统的全局参数初值。同时提出一种优化方法，在完成初步全局标定之后，利用多视点系统拍摄用于标定的标准平面镜进行重建并拼接，然后利用平面镜的平面性优化全局参数。

本文利用多视点系统扩大对高反射表面的测量范围并解决大曲率零件测量的死角问题。提出了一种多视点组合测量的方法，基于绝对点云坐标，将各视点的偏折测量结果拼接起来。同时为了约束系统误差，提出了改进的单视点系统标定与系统全局标定方法，通过利用一块标准平面镜即可完成全部标定，使多视点系统得到精确的测量结果。

1 系统测量原理

将多视点系统中的每一个视点看作一个独立的测量系统，其原理如图1（a）。使用LCD 显示屏作为参考平面，并向被测面投射相移条纹，然后采集反射后的调制图案，使用倍频多步相移法求取绝对相位，建立参考平面（屏幕）特征点空间坐标与归一化成像平面上图像点之间的密集折返对应关系。根据LIU M 的研究［24］，可以将镜面上的特征点深度s参数化，通过多项式求解获得初值。然后把镜面面型测量转化为一个优化问题：通过使参考平面上三维特征点与通过镜面反投影的对应点之间的三维误差最小，迭代地求解特征点精确深度。

图1 镜面点深度测量原理Fig.1 Mirror point depth measurement

图1（a）中，o为相机坐标系原点，m为LCD 屏幕上棋盘格靶点坐标，p为镜面反射点坐标，v=(x，y，1)为归一化像平面坐标，m和v称为反射对应。l为p处的反射光线，i为入射光线，n为p点处的法向量。设屏幕坐标系到相机坐标系的旋转矩阵和平移向量分别为R和T。

根据文献［24］，可以将被测面特征点p相对于相机坐标系原点o的深度s建模为一个偏微分方程组，并通过在已知的图像平面每一点(x，y)求解该方程组，获得关于深度s的多项式。

式中，系数D、E和F取决于标定获得的反射对应关系。一般该方程的两个解中只存在一个真值，可以将其作为初值。由此即可得到镜面反射点p与归一化像平面上点v的关系为

相应地，p点所在的法向量n可表示为

设归一化图像点坐标{v1，v1，…，vm}和参考平面上的点坐标{m1，m2，…，mm}已知，反投影原理如图1（b）。设镜面上3D 反射点对应于归一化像平面坐标(xi，yi)T可表述为pi=si(xi，yi，1)T。入射光线方向单位向量为。 反射光线方向单位向量为͂，其中令，易知r3表示屏幕坐标系Z轴方向的单位向量（屏幕所在平面的法向量）在相机坐标系中的坐标。T表示相机坐标系相对于屏幕坐标系的平移向量。设反射光线li与LCD 屏幕平面交于点，则可表示为

对于最小化问题式（5），使用LM 优化算法进行迭代计算，获得精确的镜面的深度s。将结果带入式（1），即可获得被测面在相机坐标系下的局部绝对点云坐标。

为了足够密集的获取屏幕像素点与成像平面图像点之间的对应关系。如图2 所示，采用具有四步相移的正弦条纹，并通过在屏幕上分别显示水平和竖直两个方向相互正交的条纹，实现对屏幕上每个像素点编码。其同方向上相邻两幅条纹图相位相差为，其数学表达式为

图2 相位偏折法原理Fig.2 Principle of phase deflection method

式中，n为条纹幅数，分别取1、2、…、4，由式（6）可联立方程组求解得到

式（7）求解出的相位值被包裹在[ -π，π)之间，称为相位主值，通过主值相位恢复其绝对相位称为相位解包裹过程。由于多频时间相位展开可提高绝对相位解包裹的精度且易于实现［27-28］，因此采用该方法以实现对显示器像素的编码。

2 测量系统标定

2.1 单视点标定原理

要达到测量目的，还需先对各单视点相机的内外参进行标定，目前相机内参标定已有较成熟的工业现场标定手段，如张正友标定法［21］，因此本文默认内参已知。外参标定则需要考虑到镜面测量时，相机往往不能直接观察到参考平面的问题，作者在之前的工作中［29］，通过使用平面镜作为辅助器材，使相机间接观察屏幕上靶点从而完成了相机和LCD 屏的位姿标定。

如图3，在相机坐标系中，设光学平台平面为Π，平面镜表面单位法向量为n，相机坐标系原点C到平面镜的距离为d，镜像特征点到平面镜的距离为t。则基于镜面反射，实际物点P和虚拟像点P'之间的关系可表示为

图3 LCD 屏幕标定原理Fig.3 LCD screen calibration principle diagram

式中，R′、T′为镜像靶点到相机坐标系的旋转矩阵和平移向量，可通过张正友标定法获得，R和T分别为屏幕坐标系到相机坐标系的旋转矩阵和平移向量。一般针孔相机模型为

式中，v=[xy1]T为归一化像平面坐标，I为三阶单位矩阵，PS为屏幕靶点坐标。将式（8）、（9）结合可以得到LCD 屏幕到相机的姿态转换关系。

根据式（10），至少需采集3 个镜面反射图像计算屏幕坐标系到相机坐标系的旋转矩阵R和平移向量T以及平面镜参数n、d。通过改变平面镜倾斜角度，便可以获得不同位置的镜面反射图像。每一组镜面反射图像（至少三幅），令j，j'∈{1，2，3}，R'j表示第j个平面镜位置反射图像的旋转矩阵，定义单位矢量mjj'与单位法向量nj和nj'垂直，即可得

式中，α为比例系数。进一步可列出

式中，R'j⋅R'j′T是一个特殊的正交矩阵，它有2 个复共轭特征值，且其中1 个特征值等于1。所以R'j⋅R'j'T的特征值为1 对应的特征向量，即mjj'。根据特征向量的叉积性质，可以计算三个平面镜位置分别对应的单位法向量。

求出对应3 个平面镜位置的单位法向量后，根据式（8）求解屏幕坐标系到相机坐标系的旋转矩阵Rj。在无噪声的理想情况下，分别计算得到的三个旋转矩阵Rj应该是相等的。但是实际上由于噪声的影响，三者并不相等。所以需要对旋转矩阵求平均。

旋转矩阵平均为

剩余参数[T，d1，d2，d3]T可以根据式（10）构建线性方程组求解，即

式（17）等价于

式中，D为大小9×6 的已知矩阵，c是一个大小9×1 的已知向量。这个线性系统中x的最小二乘解为x=D-1⋅c。其中D-1为D的广义逆矩阵。至此，屏幕坐标系到相机坐标系的旋转矩阵R和平移向量T以及平面镜参数n、d全部求出。

观察式（18）易知，线性解通常对噪声敏感。根据课题组之前的工作［30］，通过同时调整旋转矩阵R、平移向量T、平面镜法向量n和相机坐标系原点到平面镜的距离d，并添加共平面约束，使反投影的重投影误差最小。如图4，将LCD 屏幕上棋盘格图像移动W次，每个棋盘格位置所对应的平面镜转动M次（至少3 次）。每个棋盘格共N个特征角点。令R'ji表示第j个位置的棋盘格在第i个平面镜位置中所成镜像到相机坐标系的旋转矩阵。同理，为平移向量，nji表示镜面法向量，Rj表示第j个棋盘格坐标系到相机坐标系的旋转矩阵，Tj表示平移向量。dji表示相机坐标系原点到平面镜的距离。PSk表示棋盘格中第k个特征角点在屏幕坐标系中的坐标，Z轴方向坐标为0。qjik表示相机拍摄第j个位置棋盘格在第i个平面镜位置中所成镜像的第k个角点像素坐标，为反投影点坐标。反投影过程可表示为

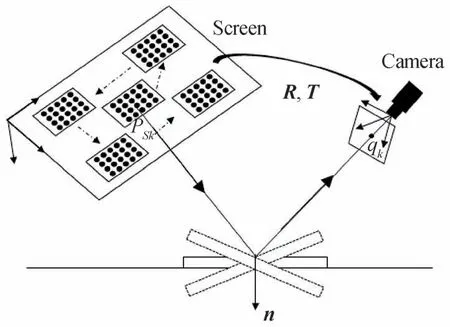
图4 标定流程Fig.4 Calibration process

式中，λji表示第j个位置棋盘格在第i个平面镜位置处的棋盘格镜像特征点从相机坐标系归一化到像平面坐标系的非零缩放因子。

式中，z为棋盘格镜像特征点在相机坐标系下的Z方向坐标，A表示相机内参数矩阵。所以反投影的重投影误差函数可表示为

由于棋盘格在LCD 屏幕上移动W次，该屏幕可视为标准平面。因此还需添加W个棋盘格图像之间的共平面约束。Pjk表示第j个位置棋盘格中第k个特征角点在相机坐标系中坐标。

设Perr为MATLAB 平面拟合函数：[fitresult，Perr] = createFit(dx， dy， dz) 的拟合效果评价值，即为平均最小距离误差。Perr值越小，共平面效果越好。该函数输入为Pjk。此外，由于棋盘格坐标系与LCD 屏幕坐标系的共平面特性，Rj，j∈{1，...，W}理论上是相等的。所以由式（15）和（16）可计算出平均旋转矩阵Rav。计算Rj与Rav的误差Rerr为

Rerr越小，共平面效果越好。同理，在光学平台上W个倾斜角为零的平面镜位置之间也具有共平面特性，所以对应的法向量nj1理论上也是相等的。同样可以计算出平均法向量nav，有

理想情况下Perr=0，Rerr=0，Nerr=0。所以代价函数可视为两部分组成：重投影误差项Errpro和共平面约束项(Perr、Rerr、Nerr)。因此，根据拉格朗日乘子法，最后建立等式约束情况下的单视点外参优化目标函数

式中，qjik表示相机拍摄第j个位置棋盘格在第i个平面镜位置中所成镜像的第k个角点像素坐标。PSk表示棋盘格中第k个特征角点在屏幕坐标系中的坐标。Rj、Tj、nji、dji为待优化参数。λre、λp、λr、λn分别为Erepro项、Perr项、Rerr项和Nerr项的拉格朗日乘子，也叫罚函数因子。LM 迭代优化求解该最小化问题，获取最佳外参，确定参考平面与相机间位姿关系。

2.2 全局标定原理

为了使测量范围更广，从而引入一个以上的视点时，需进行全局标定，将多个视点统一到一个坐标系下。如图5（a），使参考平面（LCD 屏幕）靶标保持静止，在光学平台上放置一块镜子并调整角度，使各无视场重叠相机通过镜子间接观察到唯一的参考平面，则可达到与在重叠视场放置靶标同样的效果。

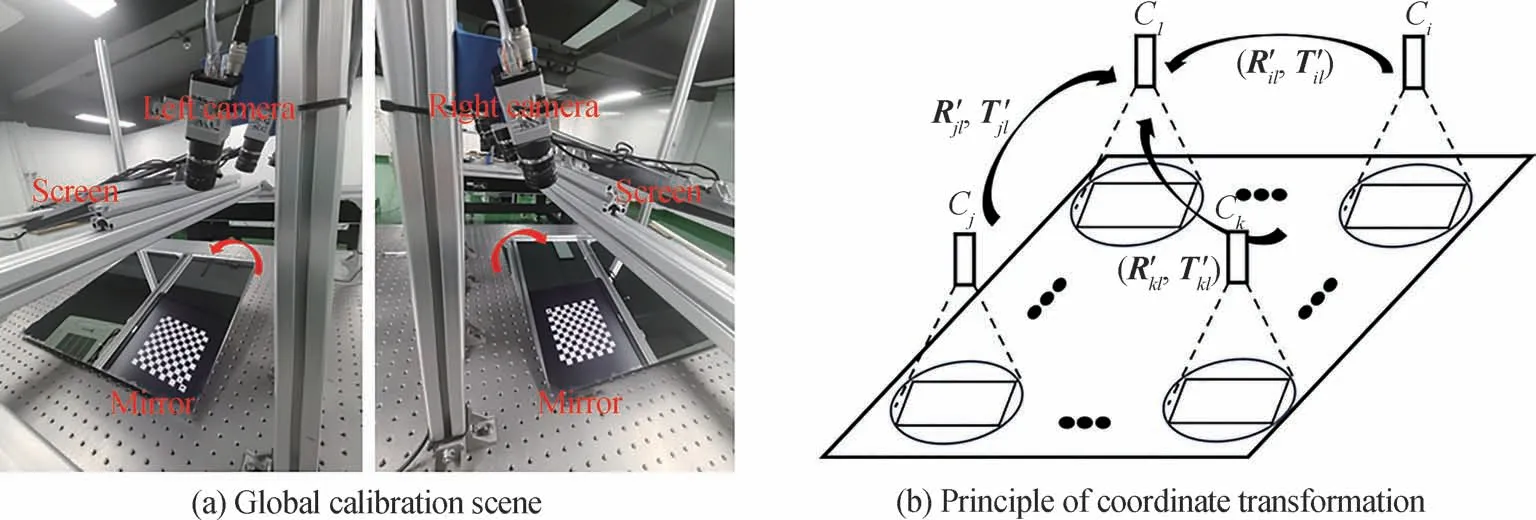
图5 全局标定原理Fig.5 Global calibration principle

式中，Pi、Pj分别为屏幕上靶点PS在相机i、j坐标系下坐标，利用2.1 节标定LCD 屏幕的方法，可通过采集不同角度镜子反射的屏幕靶点图像获得。由于参考平面靶标的唯一性，可以利用式（26）求得两个无视场重叠相机之间的姿态转换关系Rji和Tji。

以此类推，如图5（b），多视点系统可分解为若干组双镜头系统，只要保证各视点标定时的屏幕靶标一致，即可逐步完成全局标定。

由于受到噪声影响，全局标定得到的参数并不能直接使用。以双相机系统为例，假设Pki、Pkj分别表示棋盘格第个k靶点在i、j号相机坐标系下的坐标，分别表示相机i坐标系向相机j坐标系转换的旋转平移矩阵，则基于式（26），Pkj通过相机可以构造误差函数

利用标准平面镜的平面性质，使用多视点系统对放置在光学平台上的标准平面镜进行测量，理论上任意双相机系统统一坐标系之后，对拼接后的重建结果使用平面拟合函数，拟合误差应该为0。据此可以利用该先验性质建立约束进一步优化全局标定参数，使用MATLAB 平面拟合函数拟合效果评价值作为约束，即

式中，输入为点云坐标。最后根据拉格朗日乘子法，建立等式约束情况下的全局参数优化目标函数

同理，λt、λc为罚函数因子，LM 法迭代优化求解该最小化问题，获取最佳全局外参，确定相机间位姿关系。

整个标定过程如图6。通过利用镜像靶点进行标定，获得各视点在镜像下的外参R′，T′；利用式（13）计算特殊正交矩阵R'j⋅R'j′T（j=1，…，3）特征值1 对应的特征向量mjj'，然后利用式（14）计算每个棋盘格位置对应的三个平面镜位置的法向量nj，再通过求解式（8）、（17）得到各视点的真实外参R，T与镜面参数T，dj；将得到的外参与镜面参数作为式（15）优化函数的初值，并添加共平面约束进行迭代之后，便能得到精确的外参，从而完成真实相机标定；最后，利用式（26）得到全局外参初值，将各视点统一在唯一坐标系下，并对标准平面镜进行测量，利用优化函数（29）得到精确的全局参数；在每个视点，重复上述过程，利用式（26）将各视点重建结果统一在某一个主视点下，达成多视点测量的效果。

图6 标定与测量流程Fig.6 Flowchart of the calibration and measurement

3 实验结果与分析

为了验证所提出的标定及测量方法的准确性，设计了多视点视觉系统测量实验。图7 展示了整个测量系统的基本结构：光学平台、标准平面镜、LCD 显示屏以及4 组相机。其中LCD 显示屏的型号为戴尔P1917S，屏幕分辨率为1 280 pixel×1 024 pixel，像元尺寸为0.293 mm×0.293 mm，四个相机的型号为大华A5201MG50，相机的分辨率为1 920 pixel×1 200 pixel，像元尺寸为4.8 μm×4.8 μm。配合Computar 工业镜头使用，镜头型号为M1620-MPW2。

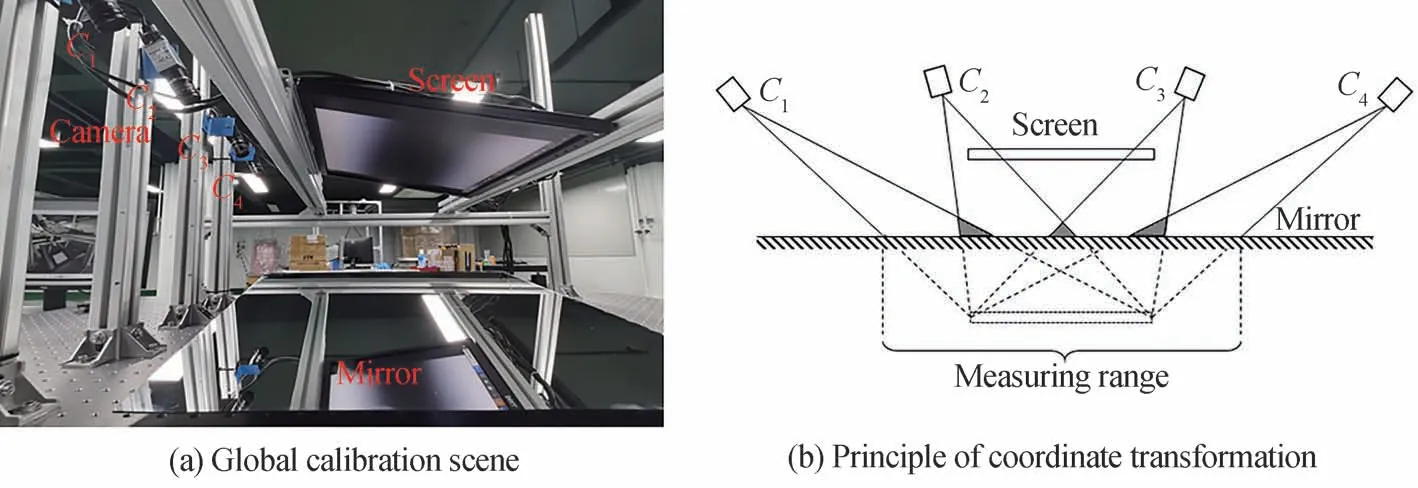
图7 多视点测量系统Fig.7 Multi-view measurement system

首先，使用任意相邻两组相机对一块球面半径为467.5 mm 的球面透镜进行测量并进行拼接。图8（a）为无约束的重建结果，可以观察到明显的缝隙，这是由于视点几何标定和全局标定过程中产生的系统误差引起的，如图6 所示，该测量系统为线性系统，前期标定过程中的误差在测量中会成倍放大。图8（b）为添加约束的重建效果观察到缝隙消失，重建表面光滑，证明了所提出共面约束的有效性。因此后续试验均采用添加约束的标定参数。

图8 平面约束对重建的影响Fig.8 The influence of plane constraint on reconstruction

如图9，将一块500 mm×500 mm 尺寸的标准平面镜和球面半径为467.5 mm 的球面透镜分别放在光学平台上，利用多视点系统对其进行测量，以验证本方案在大尺寸、大曲率测量场景下的有效性。其中，平面镜制造工艺为前镀膜浮法玻璃，面型误差小于0.002 mm，可视为标准平面，实验中使用最多4 相机组成的阵列进行测量。与之相比，具有更大曲率的球面透镜面型精度为四分之一波长（587.6 nm），可视为标准球面镜，实验中使用左右相机组成的双相机阵列进行测量。相机测量视角与结果点云分别如图9（a）、（c）和（b）、（d）。将获得的点云数据与理想模型进行拟合，求得均方根误差（Root Mean Square Error，RMSE）作为测量误差，其中，4 视点系统平面镜测量误差为0.086 mm，双视点系统球面镜测量误差为0.064 mm。

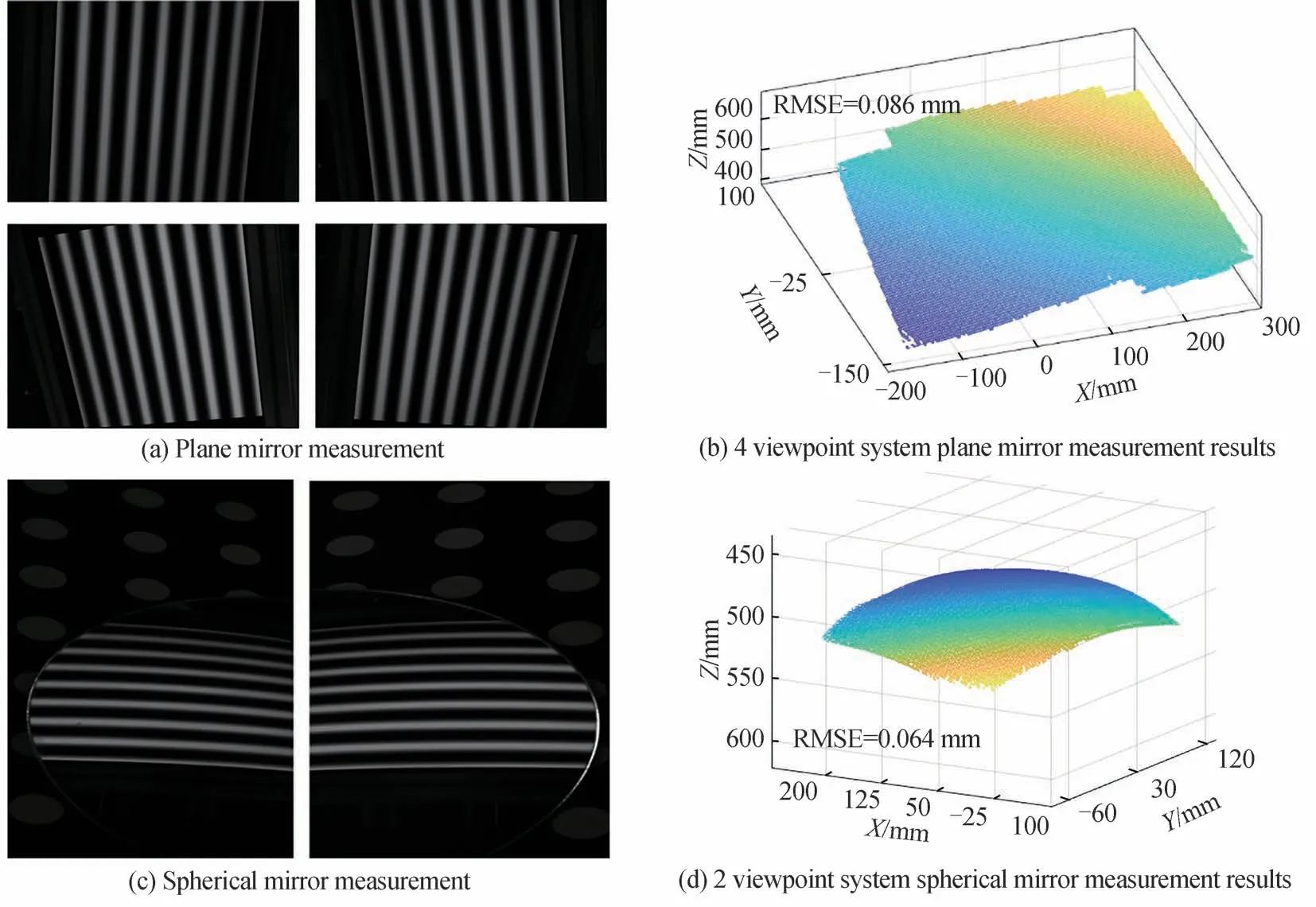
图9 多视点系统测量结果Fig.9 Measurement results of multi-view system

同时，通过点云处理软件的表面积量算功能可获得不同数量视点测量下重建结果的点云表面积。以平面镜多视点测量为例，其统计结果如表1。

表1 多视点系统平面镜测量结果Table 1 Plane mirror measurement results of multi-view system

测量结果表明，在大尺寸场景，所提方法通过增加视点数量，使测量范围相比单视点测量范围大幅增加，而误差递增平缓，在0.1 mm 以内。而在大曲率场景下，整体测量难度提高，但通过视点拼接，本文方法依然达到了较高的精度。

考虑到测量范围与误差的均衡，将视点数量固定为4，然后将一块高度为8.89 mm 的标准量块放置于光学平台和被测标准平面之间，使镜面位置较之前升高。再对升高的镜面进行测量并拟合，接着利用点到平面距离公式计算两个拟合镜面间的平均距离，将其与标准件高度进行比较。两个镜面位置的镜面恢复点云如图10（b）。

图10 台阶面测量结果Fig.10 Step surface measurement results

最后，如图11，经过重复试验并取平均值，测量量块高度与实际高度误差小于0.1 mm，间接验证了本文测量方法的准确性。

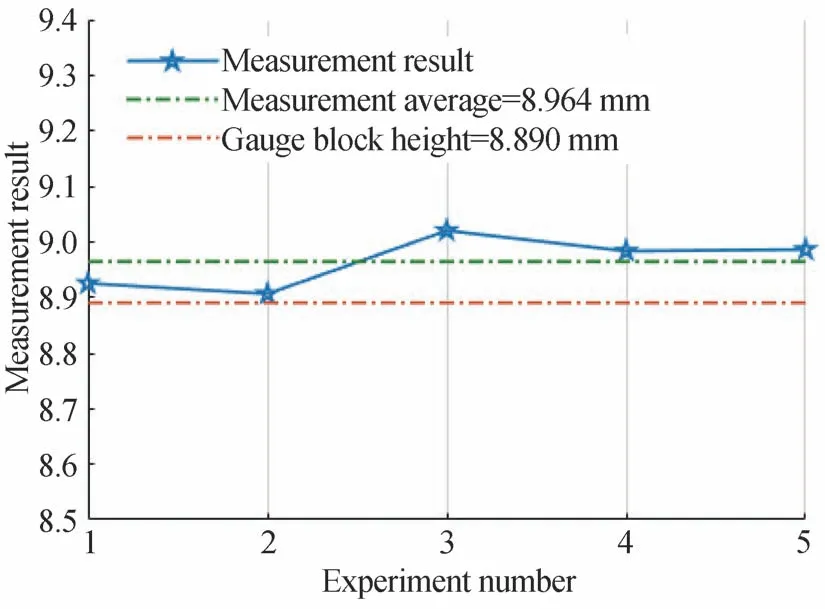
图11 台阶面测量结果统计Fig.11 Statistics of step surface measurement results

4 结论

本文利用多个相机阵列组合实现了对高反射面面形的便捷性检测。相对于单相机测量系统，该多视点系统可根据实际情况，灵活设计相机数量和排列方式，尤其在大尺寸、大曲率高反表面测量时，可有效规避盲点并扩大测量范围。采用了改进的显示器屏幕标定方法和全局标定方法，利用显示屏和平面镜的平面性抑制标定误差，仅需标定一次，且所需器材仅有一块标准平面镜。在所提出的方法中，重建结果精度主要取决于显示器编码和系统标定精度，为此可以使用更高分辨率的显示器和相机系统或更高精度的相移解包裹算法提高测量结果精度。对于透明光学镜面，非连续性镜面等特殊测量场景，如何使用所提方法完成高精度的便捷性测量是进一步研究的方向。