非局域超表面微分器的逆向设计

秦浩然，寇君龙，朱家荣，周子昕，王军转，陈召宪，陆延青

（1 四川大学 物理学院，成都 610065）

（2 南京大学 集成电路学院，苏州 215163）

（3 南京大学 电子科学与工程学院，南京 210093）

（4 苏州大学 机电工程学院，苏州 215021）

（5 南京大学 现代工程与应用科学学院，南京 210093）

0 引言

微分器可以视为高通滤波器，能够滤除信号中的直流分量与低次谐波分量，提取并增强其中的高次谐波分量。空间微分器提取和增强的信息对应的是入射图像的边缘［1］。边缘提取与增强技术在数据压缩、缺陷检测等应用中有着不可或缺的作用［2］，在过去几十年，一直是热门的研究课题［1-6］。

与电路相比，用光作为传输载体的空间微分器在速度、功耗与可靠性方面具有很大的优势［7］。然而，用传统的光学介电透镜构成的空间微分器在准确性与边缘识别效果方面仍然不尽如意，归根到底是因为它们庞大的体型使得光在反射过程中产生的损耗和球型表面引起的像差不可忽略，此外，光还存在着衍射极限［8］。亚波长尺度的光学超表面能够突破传统光学透镜的上述限制。通过定制光在传播过程中的路径与振幅和相位等参数的变化［9］，研究人员设计了大量能够精确实现空间微分运算的结构［1-6，10-13］。通过有意地扰动一个过调制的随机散射系统，SOL J 等［4］设计了一种超表面解码矩阵来执行可编程的高阶微分，该系统表现出高保真度和灵活性。此外，ZHOU J 等［13］提出了一种基于几何相位超表面实现空间微分的机制，通过实验验证了所设计结构的高光学效率和高带宽。

上述成果具有开创性，特别是在一些性能指标上令人振奋。但这些设计策略往往只关注于某个特定的应用场景，而忽略了其通用性。为了弥补这一缺点，我们将优化算法与光学非局域超表面的逆向设计相结合［14-16］。通过确认目标、优化结构、验证功能等设计步骤［17］，充分利用超表面各个像素间的相互作用［16］，可以实现各种运算逻辑［16，18-23］。EGOROV V 等［19］利用遗传算法优化圆柱体磁盘的半径，实现了一个带宽大，效率高的光偏转器。此外，CAI H 等［16］利用遗传算法，优化圆柱体元透镜的半径分布使其相互耦合，拟合对应结构的相位轮廓，实现了一个效果好且厚度薄的非局域聚焦透镜。

受以上研究的启发，本文利用遗传算法完成了两个超表面光学器件的逆向设计，使其分别能够实现一维二阶空间微分和拉普拉斯变换。设计中，对非局域超表面的材料分布进行优化，使其传递函数接近设计目标，即入射角和透过率之间满足二次函数关系，进而实现二维空间微分运算［8］。

一维二阶微分器的优化效果很显著，最优解与理论解传递函数之间的误差随着迭代的进行逐渐下降（从1.16×10-1下降到6.18×10-5）。当入射角小于10°时，两者高度吻合。在拉普拉斯变换器优化过程中，最优解的传递函数与理论解之间存在一定的差距。由于算法本身收敛速度快，得到的解可能是局部的最优解。验证发现该结构仍具有空间微分与边缘识别的功能，因此，本文提出的逆向设计方法具有很强的通用性与容错率。

1 一维二阶微分器

1.1 基本原理

在一维情况下，假设光沿x方向进行空间微分运算，f（x）表示入射波沿x轴的电场分布，g（x）表示光通过超表面后透射波的电场分布。g（x）与f（x）之间的关系为

式中，（I）FT 代表（逆）傅里叶变换，H（kx）代表超表面的传递函数，即以波矢量（kx）为自变量的透过率。当H（kx）与kx2成正比时，根据式（1）可知g（x）等于f（x）的二阶导数乘以一个负系数。考虑到入射角和波矢量在数值上相等，传递函数等价于入射角和透过率之间的关系。因此当传递函数接近二次函数时，就可以实现二阶微分运算［8］。由于此时透过率与波矢有关，该结构必然要利用超表面各像素间的电磁耦合，因而是非局域超表面［24］。

1.2 建模

整个微分器模型由方形排列的周期性晶胞单元组成，每个晶胞单元如图1（a）所示，其中蓝色代表二氧化硅，红色代表硅，灰色代表空气，周期D=400 nm。晶胞单元包括二氧化硅衬底和其上厚度h=160 nm 的超表面。每个超表面包含10×10 个独立像素，其中每个像素都由空气或硅构成。为提高优化效率，我们将超表面的材料分布设置为关于y轴对称，在这样的约束下得到的传递函数也是对称的。值得注意的是，仿真时为提高运算速度，将x和y方向的网格尺寸都设置为10 nm，小于像素的边长（40 nm）。因此，实际的材料分布需由折射率检测器确认。将波长为730 nm 的平面波入射到超表面上，功率探测器放置在超表面下方以监测透射率。

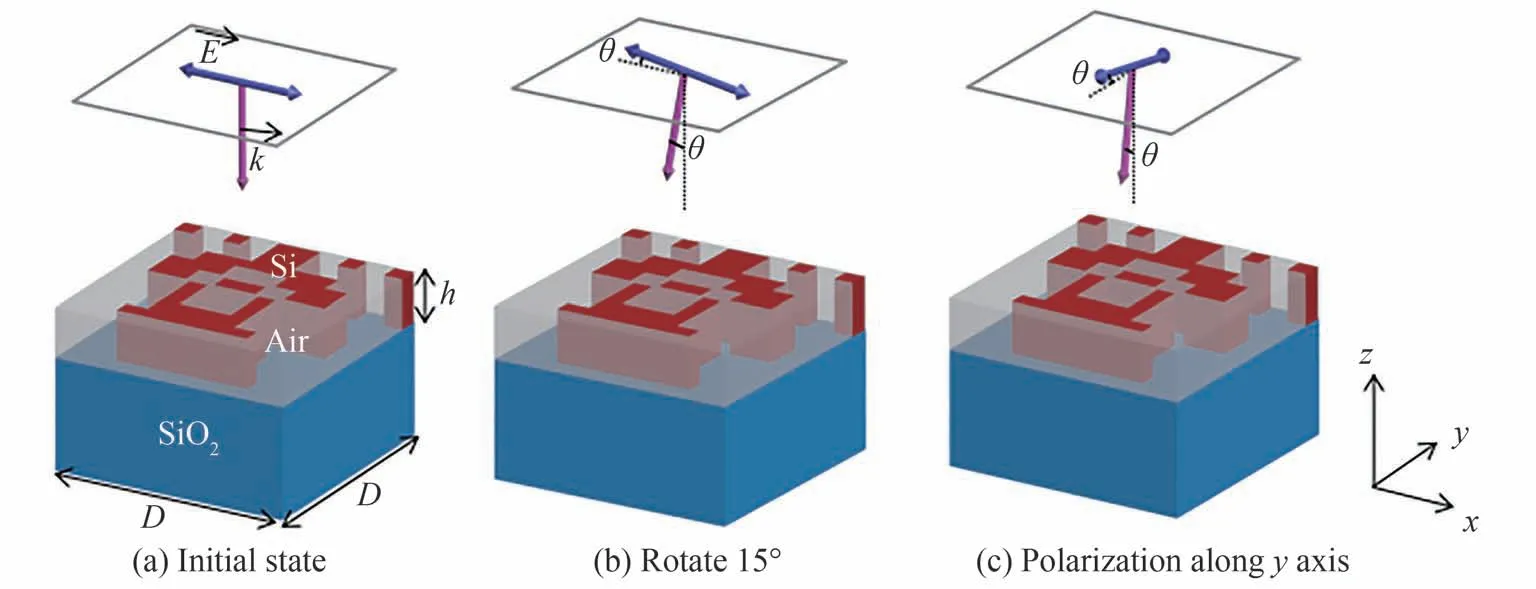
图1 不同运算状态下的模型Fig.1 Models in different operating states

在初始状态下，入射波的偏振方向沿x轴，入射方向沿z轴反方向。然后在xoz平面上以入射波中央为中心顺时针旋转θ，使入射角等于θ，如图1（b）所示，其中θ等于15°。此外，对于在y方向上进行微分的场景，我们只需要将入射平面波的初始偏振方向更改为沿y轴，旋转平面更改为yoz平面，如图1（c）所示。为了实现二阶微分，传递函数应接近二次函数。为了在保证优化效果的同时尽可能减少计算时间，我们将目标函数（用FOM 表示）设置为

式中，T（θ）是当入射角等于θ时的透过率。FOM 的设置在简便性与准确性之间取得了平衡：首先，模型只会有三种状态（对应θ等于0、5°和10°），相当于在所优化的结构对应的传递函数和理论曲线上拟合了三个点；其次，为了让T（0），即垂直入射时的透过率优先趋近于0，将其乘以10 作为权重。只要入射角不是太大，就可以满足入射角与透过率之间的二次函数关系，进而实现入射波和透射波场强分布之间的二阶微分关系。对于入射角超过10°的情况，由于其不满足傍轴近似的条件，通常不予考虑。此外，改变式（2）中0.1 和0.4 的值，可以拟合出具有不同前置系数的二次函数。

1.3 算法与迭代

为了减少迭代次数，本文选择收敛速度更快的遗传算法［25］。其基本流程［17］包括：1）编码并生成初始种群：每个个体的超表面材料选择对应10×10 的二值化矩阵（其中0 代表空气，1 代表硅），随机生成10×10×20 的二值化矩阵作为初始种群（即第一次迭代的父代，其中20 为个体数）；2）交配：将20 个父代个体两两配对，交换其部分取值，生成子代；3）淘汰：计算每个个体的FOM，记录其中的最小值，将父代和子代中一半适应性更强（即FOM 更小）的个体筛选出来，作为下一次迭代的父代。4）结束：重复2）和3）两步，直到迭代次数达到预设值或最优解的FOM 小于FOM 的预设值。

该算法连续性好，但多样性较差，也就是说容易算出局部最优解。为了加快迭代速度，这样的牺牲是值得的。事实上，入射角和透过率之间并不一定要严格满足二次函数关系，只要垂直入射时的透过率小于10-2，得到的器件结构就具有一定的微分功能。由于该方法的高容错率，并不需要算法本身具有很高的智能性。

使用此算法迭代至多50 代，每代包含20 个父代和20 个子代（通过代码可以记录下已经计算过的结构，避免没有必要的重复运算）。每个个体的FOM 是使用时域有限差分法计算得到的。随着迭代的进行，每个个体的FOM（以10 为底取对数以提高对比度，用lg（FOM）表示）及每次迭代的最优个体的FOM（以10 为底取对数，用min［lg（FOM）］表示）分别如图2（a）和图2（b）所示，其中图2（a）中每个色块代表一个个体。

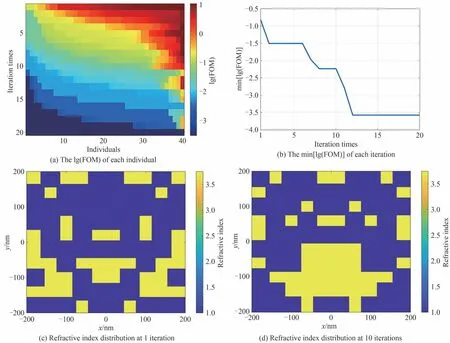
图2 最优解的折射率分布及其传递函数随迭代次数增加的演化Fig.2 Evolution of refractive index distribution and transfer function of optimal solution as the iterations increase

在优化过程中，某一次优化所得最优解的FOM 及其对应的折射率分布如图2（c）～（f）和表1 所示。可以看到，随着迭代的进行，最优解的FOM 从1.16×10-1逐渐下降到6.18×10-5。特别是入射角小于10°时，优化后的传递函数更接近理论上的二次函数。

表1 最优解随迭代次数增加的演化Table 1 Evolution of optimal solution as the iterations increase

1.4 可靠性评估

实际制造中的误差不可避免，特别是在周围材料均与之不同的像素（又称孤立像素）上，因此可靠性评估是必要的。在进行可靠性评估时，对上节中迭代次数为30 次时得到的最优解对应的材料分布进行适当更改后计算其目标函数或传递函数，并比较更改前后的结果。

设计了两个可靠性评估。更改后的材料分布（其中更改的部分用红框标出）及其对应的传递函数如图3所示。从中可以推断出，在第一种更改下，传递函数仍然有二次函数的形状，FOM 上升到了5.29×10-3；在第二种更改下，FOM 上升到了3.23×10-2，此时仍可以实现边缘检测的功能。

图3 一维二阶微分器的可靠性评估结果Fig.3 Reliability assessment of one-dimensional second-order differentiator

图3（d）是超表面的切换图分析结果［20］，其中每个色块代表对应像素单独发生转换（从空气变成硅或反之）时，用转换后的目标函数（用FOM_tog 表示）减去最优解对应的FOM（均以10 为底的对数）。从中可以看出所得结果均为正数，这说明转换后的结构均不如本文方法得出的最优解。

1.5 功能验证

为验证得到的最优解能否实现一维二阶的空间微分，首先周期性地排列30×30个晶胞单元，并入射沿x方向偏振、沿z轴反方向入射的高斯波。图4（a）和图4（b）分别是入射波与透射波电场x分量的分布，图4（c）是图4（b）在y=0 处的截线。作为第二个验证示例，用平面波替换高斯波，入射到30×15 个晶胞单元周期排列的器件结构中间（四周没有光波入射）。所得透射波的电场x分量分布如图4（d）所示。

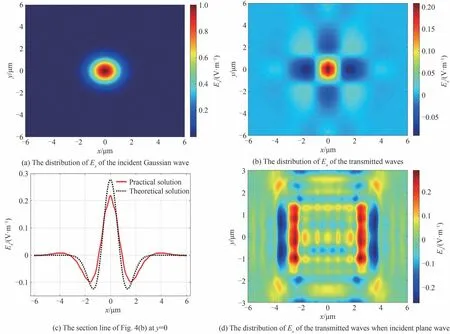
图4 一维二阶微分器的功能验证Fig.4 Functional verification of one-dimensional second-order differentiator

从图4（c）中可以看出，仿真得到的实际波形与理论波形，即高斯波的二阶导数乘以一个负系数（-0.166 3）相似。可以推断出，该超表面的能量转换率略小于16.63%。此外，从图4（d）可以看出，透射波在x方向上反映了入射波的轮廓，且一个轮廓对应两个峰值。因此，该结构在x方向上实现了二阶空间微分。

2 拉普拉斯变换器

为了证明本文提出的方法具有很强的通用性，本节采用类似的方式设计了一个拉普拉斯变换器。迭代时，需要计算入射波沿x轴和y轴极化时的透过率，分别对应图1（b）和图1（c）中的模型。为了简化运算，将超表面的材料分布设置为同时相对于x轴和y轴对称。与式（2）类似，此时的目标函数（用FOM_xy表示）设置为

式中，Ti（θ）表示入射波的偏振方向沿i轴（i=x或y）且入射角等于θ时的透过率。在确定FOM_xy时，我们提高了垂直入射时透过率的优先级，同时降低非垂直入射时透过率的目标取值以提高目标曲线的平滑度。我们使用与先前设计一维二阶空间微分器相同的算法和参数来进行优化。所得最优解的材料折射率分布和传递函数分别如图5（a）和图5（c）所示，其中Tx（0）、Ty（0）和FOM_xy分别等于2.74×10-3、1.05×10-2和8.84×10-3。

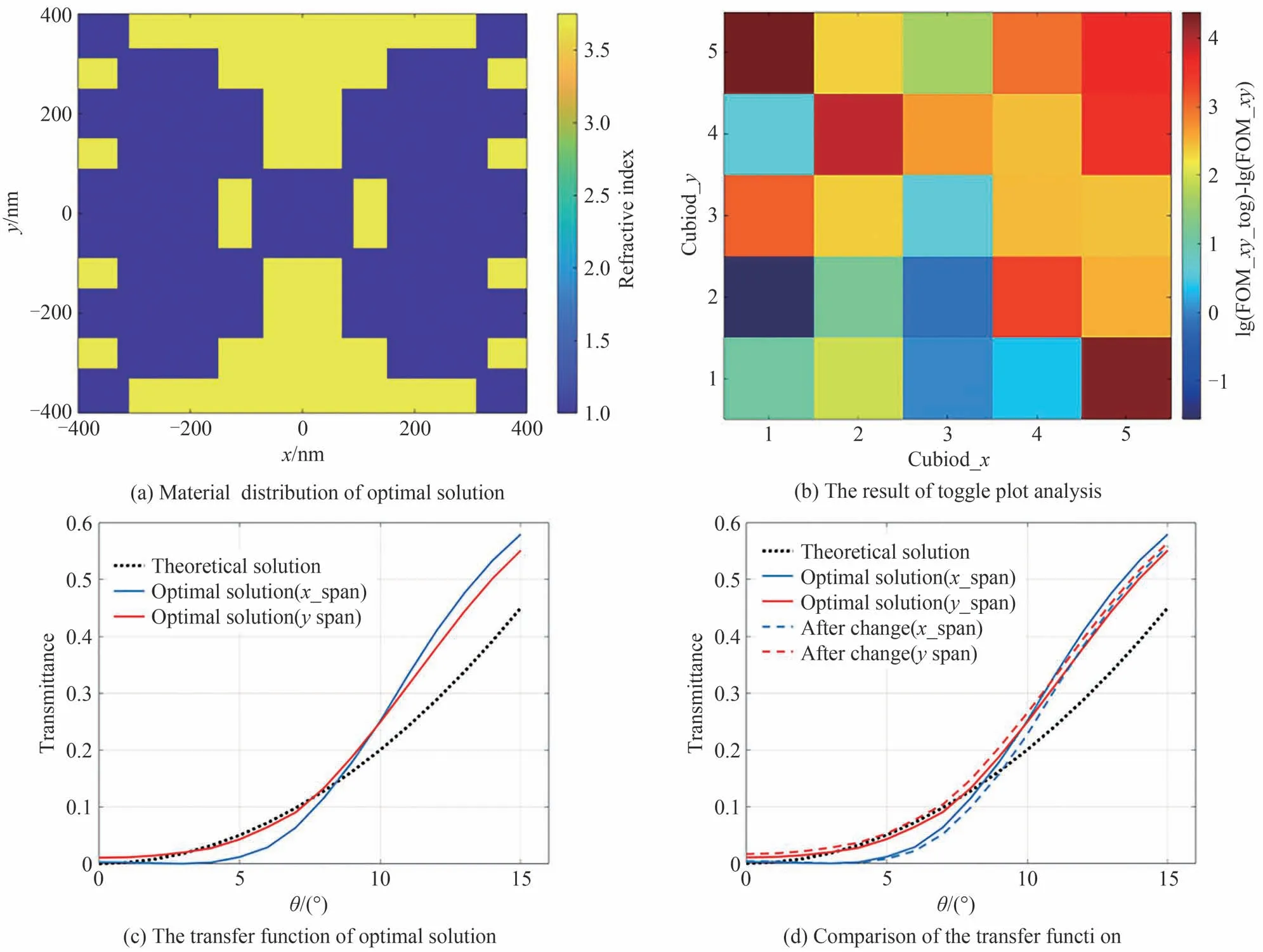
图5 拉普拉斯变换器的最优解Fig.5 Optimal solution of Laplace transformer

对该最优解进行可靠性评估。将x方向边界处的孤立像素适当扩大（对应工艺中没有刻蚀完全），并比较更改前后的结果，如图5（d）所示。更改后，FOM_xy上升到1.24×10-2，仍能实现边缘检测。需要注意的是，这种结构只是一次优化得到的最优解，而不是算法的极限解。在图5（b）所示的切换图中，可以很容易地找到更好的解，其中FOM_xy_tog 表示转换后的目标函数。

为验证本文设计结构确实具有识别图像轮廓的功能，进行两个仿真测试。首先，周期排列30×30 个晶胞单元，在整个器件结构的中间入射偏振方向与x轴成45°角的平面波（四周没有光波入射）。然后，使用镂空的金属银作为入射平面波与50×40 个晶胞单元周期排列成的器件结构之间的阻挡层，阻挡层仅允许一个“N”形状空间分布的平面波通过。

第一个测试中得到的透射波电场的x和y分量分布分别如图6（a）和图6（b）所示，从中可以看出，透射波在入射波边缘沿偏振方向出现尖峰，且一个边缘对应最大和最小两个峰值。因此，该结构可以实现拉普拉斯变换。两个测试的电场强度的分布分别如图6（c）和图6（d）所示，从图6（d）中可以很清晰地看出字母“N”的轮廓，且每一个边缘对应场强中的两个峰值，其中斜线部分的轮廓是x和y方向上场强的重叠而成的。

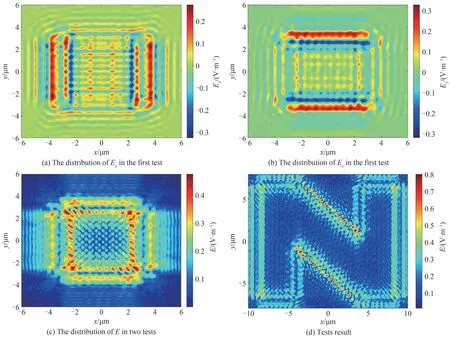
图6 拉普拉斯变换器的可靠性分析与功能验证Fig. 6 The reliability assessment and functional verification of Laplace transformer

3 结论

利用遗传算法优化非局部超表面的材料分布，设计并验证了一维二阶微分器和拉普拉斯变换器。本文设计的结构可用于识别和增强图像轮廓，具有小型化和高速化的特点。该方法可以扩展到其他空间运算的设计，例如积分或空间滤波。考虑到该方法对算法本身和制造过程有着较低的要求和较高的容错率，该方法在设计光学计算单元方面具有巨大的潜力。此外，可以将迭代过程中得到的所有材料分布及其传递函数一一对应起来，形成一个数据库，结合深度学习研究结构参数与其电磁响应之间的映射关系，进而代替时域有限差分法来完成逆向设计，进一步提高优化效率。