基于改进狮群算法的最大功率跟踪控制研究

潘海鹏, 吴小峰, 雷美珍

(浙江理工大学信息科学与工程学院, 浙江 杭州 310000)

0 引言(Introduction)

全球能源供应的不断减少和环境污染问题日益严峻,人类更加积极地寻找可持续发展的新型能源。波浪能是一种储存量丰富且开发前景乐观的可再生能源[1]。因此,合理地开发波浪能,能够有效地缓解人类的能源危机。

最大功率点跟踪(Maximum Power Point Tracking,MPPT)是当今新能源领域的研究热点,已成为提高光伏发电[2]和风力发电[3]系统效率的一种有效方法。WANG等[4]提出了一种变步长扰动观察法,通过对步长的自适应调节,减小了系统在最大功率点的振荡,提高了能量的转换效率,但仅考虑了规则海浪波的情况,在实际的非规则海浪波中可能无法达到仿真的效果。潘海鹏等[5]将遗传算法引入波浪发电最大功率点跟踪控制中,采用遗传算法计算发电系统最大功率点对应的参数,实现发电系统在非规则波浪情况下的最大功率跟踪控制,但发电系统最大功率点对应的参数易陷入局部最优。

通过智能优化算法求解发电系统的最优参数,是实现波浪发电最大功率输出的有效途径之一。本文采用了基于改进狮群算法的最大功率点跟踪算法,引入Tent混沌初始化、差分进化算法和灰狼优化算法后,仿真结果表明在非规则海浪的情况下,该方法能提高直驱式波浪发电系统的最大功率输出。

1 直驱式波浪发电系统数学模型(Mathematical model of direct drive wave power generation system)

图1为直驱式波浪发电系统的结构示意图,该发电系统主要由浮子、永磁同步发电机和变流器等部分组成。浮子和永磁同步发电机的动子直接相连,动子通过浮子的运动进行垂直方向的运动,动子切割磁场,生成电能,产生的交流电再通过变流器转换直流电,并与负载连接。

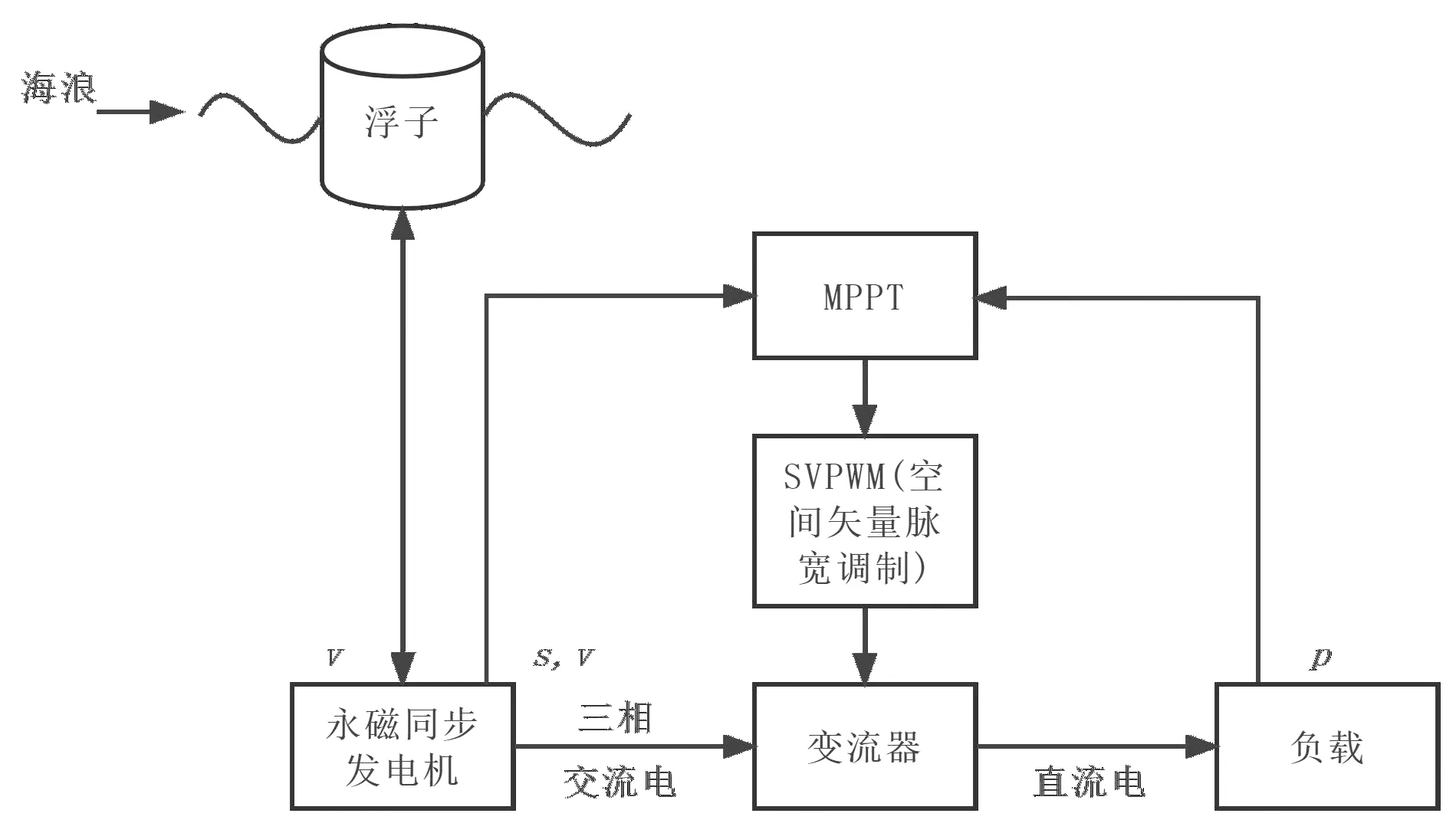
图1 直驱式波浪发电系统结构图Fig.1 Structure diagram of direct drive wave power system

浮子在海浪中受到多个方向力的作用,但永磁同步发电机的动子只在竖直方向上运动,所以只分析浮子在垂直方向上的运动,根据牛顿第二定理可得[6]:

(1)

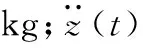
假如浮子是圆柱状,则浮子所受到的浮力正比于其偏移的距离,假设浮子在未受到海浪作用力时的位置为平衡位置,则:

Fb(t)=-ρgz(t)+mg=-Kz(t)+mg

(2)

公式(2)中,ρ表示海水密度,单位为kg/m3;z(t)表示浮子的位移,单位为m;K表示静浮力系数。

在规则海浪波驱动的直驱式波浪发电系统中,永磁同步发电机的电磁力与速度、位移之间的关系可以表示如下[7]:

(3)

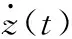
结合公式(1)至公式(3),可得到系统的动力学方程:

(4)

公式(4)中,ma表示海浪频率趋于无穷时的附加质量,单位为kg;Ra表示阻尼系数。

忽略永磁同步发电机的电磁损耗,系统的瞬时功率可以表示如下:

(5)

波浪发电输出的功率并不恒定,会随着浮子运动不断发生变化,系统的瞬时功率无法反映波浪发电的特点,因此有必要对一段时间内系统输出的平均功率进行研究。为此,从频域上分析系统可以得到更好的效果,公式(4)在频域上的表达式如下:

(6)

直驱式波浪发电系统输出的复功率的实部可以表示为从海浪中提取的平均功率[8]:

(7)

发电系统输出的平均功率:

(8)

从公式(8)中可以看出,直驱式波浪发电系统的理论最大功率:

(9)

公式(8)中的最大功率是在规则海浪波的情况下得出的直驱式波浪发电系统的最大功率,从中可以看出要实现最大功率跟踪控制,可以通过计算解出最大功率点所对应的rg和kg,而在实际海域中的海浪状况是不断变化的,根据线性叠加的原理,实际海域中的海浪可以等效成为无数个不同的正弦波组合。文献[9]和文献[10]中提出可以将实际海域中的不规则海浪波分解成若干个正弦波,并建立海浪频谱表征海浪的状态。

根据海浪波谱和线性叠加原理可得到海浪波高和海浪激励力之间的公式[11]:

(10)

公式(10)中,δ(t)表示海浪波高,单位为m;Ai表示第i个海浪波的幅值,单位为m;ω表示海浪的频率,单位为rad/s;εi表示分布在[0,2π]的随机偏差角。频率等分法是将所取得的频率平均划分为n个区间。

通过对非规则海浪和规则海浪波之间关系的分析,可以得到系统在非规则海浪情况下的平均输出功率:

(11)

从公式(11)中可以看出,非规则海浪驱动下的波浪发电系统也是通过计算出最大功率点所对应的rg和kg,达到发电系统的最大功率输出。

2 基于改进LSO的MPPT控制算法(MPPT control algorithm based on improved LSO)

2.1 基础的LSO

LSO是将问题的最优解视为猎物所在的位置,将各头狮子的位置作为可行解。狮群算法分为成年狮和幼狮,成年狮中包括1头狮王(公狮)和若干头母狮,狮王的位置是每代狮群中适应度最好的位置。狮群算法的步骤如下。

(1)初始化参数:随机生成N头狮子的位置,成年狮的数量为NL,其中公狮的数量为1头,其余为母狮的数量,幼狮的数量为N-NL,其中NL取值范围如下:

(12)

(2)适应度计算:计算适应度,将个体历史最优位置设置为各狮子当前的位置,将适应度最好的位置设为狮王的位置。

(3)狮群位置更新:捕猎中不同狮子的位置移动方式不同,狮王围绕最佳位置进行小范围移动,位置更新公式如下:

(13)

母狮在捕食的过程中需要与另1头母狮协作,更新位置如下:

(14)

幼狮更新位置如下:

(15)

(16)

(17)

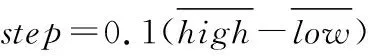
(18)

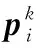
(19)

(4)适应度对比:通过迭代更新后的种群适应度与上一代适应度做对比,若本次种群的适应度更好,则将上一代中的自身历史最优位置和种群最优位置替换掉,使解向最优解靠近。

(5)判断终止条件:将当前的适应度与上一次的适应度做对比,若两者间的误差不大于当前适应度的5%,并算法的迭代次数为15次以上,则结束算法,输出最优解,否则返回“步骤(3)”,直至迭代次数为最大时,输出最优解。

2.2 LSO的改进

2.2.1 混沌映射的种群初始化

为了保证初始化种群的均匀分布且具备多样性,在算法的初始化群体中引入Tent混沌映射,混沌映射具有随机性、遍历性的特点,常被用作优化算法的一种改进方法,它有利于维持种群的多样性和提高算法的局部搜索能力,Tent混沌映射生成的序列如下:

(20)

公式(20)中,n表示种群个数;u表示均匀分布在[0,1]的随机数。结合Tent混沌映射,进一步生成搜索区域内狮群的初始群体位置:

xi=low+T(n)×(high-low)

(21)

2.2.2 母狮的位置更新机制改进

针对狮群活动范围较大时,狮群位置容易越界,在母狮的位置更新中引入差分进化算法,则母狮的位置更新如下:

(22)

F=Fc×2α

(23)

(24)

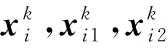
2.2.3 幼狮的位置更新机制改进

为了大部分幼狮能向最优位置和母狮靠近,其余幼狮随机游走,在幼狮的位置更新中引入灰狼优化算法中的狼群的捕猎机制,则幼狮的位置更新如下:

(25)

(26)

(27)

(28)

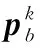
2.3 改进狮群算法在MPPT中的应用

改进狮群算法需要设置的参数少,性能良好,适用于求解直驱式波浪发电系统的最大功率跟踪控制优化问题。改进狮群算法在发电系统的具体应用如下。

(1)初始化参数:随机生成50头狮子的位置,其中狮王的数量为1头,母狮的数量为9头,幼狮的数量为40头,最大迭代次数设为100次。

(2)适应度计算:将公式(8)作为适应度函数,将适应度最好的位置设为狮王的位置。

(3)狮群位置更新:根据公式(13)、公式(24)和公式(28)更新狮王、母狮和幼狮的位置。

(4)适应度对比:通过迭代更新后种群的适应度与上一代适应度做对比,若本次种群的适应度更好,则将上一代中的自身历史最优的rg、kg和种群最优的rg、kg替换掉,使解向最优解靠近。

(5)判断终止条件:将当前的适应度与上一次的适应度做对比,若两者间的误差不大于当前适应度的5%,并且算法的迭代次数为15次以上,则结束算法,输出最优解,否则返回“步骤(3)”,直至迭代次数为最大时,输出最优解。

改进狮群算法的算法流程如图2所示。

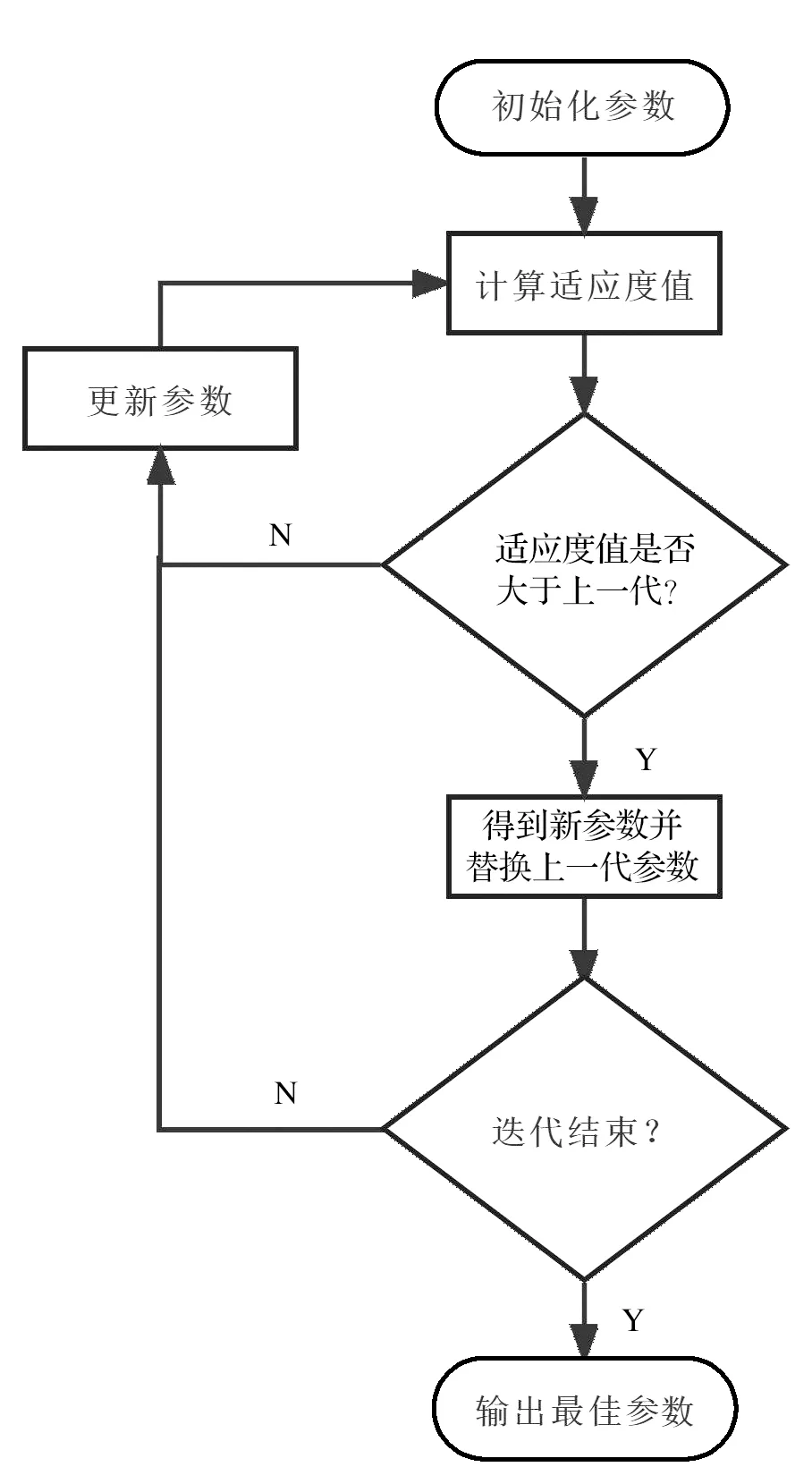
图2 算法流程图Fig.2 Algorithm flow chart

3 仿真分析(Simulation analysis)

在MATLAB的仿真工具Simulink中搭建直驱式波浪发电系统的仿真模型,将提出的改进狮群算法与基础狮群算法以及遗传算法进行对比,证明本文所提算法的可行性和有效性。其中,仿真模型的参数如表1所示。

表1 仿真系统参数Tab.1 Parameters of the simulation system

智能优化算法辨识最优参数的速度对于直驱式波浪发电系统至关重要,因此进行20次仿真对比改进狮群算法、遗传算法及基础狮群算法的运行时间(如图3所示),在20次仿真时间中,改进狮群算法的时间略长于遗传算法和基础狮群算法,运行时间集中于0.3～0.4 s,而本文研究中的海浪周期为4 s,海浪周期内可以实现最优参数的实时计算。

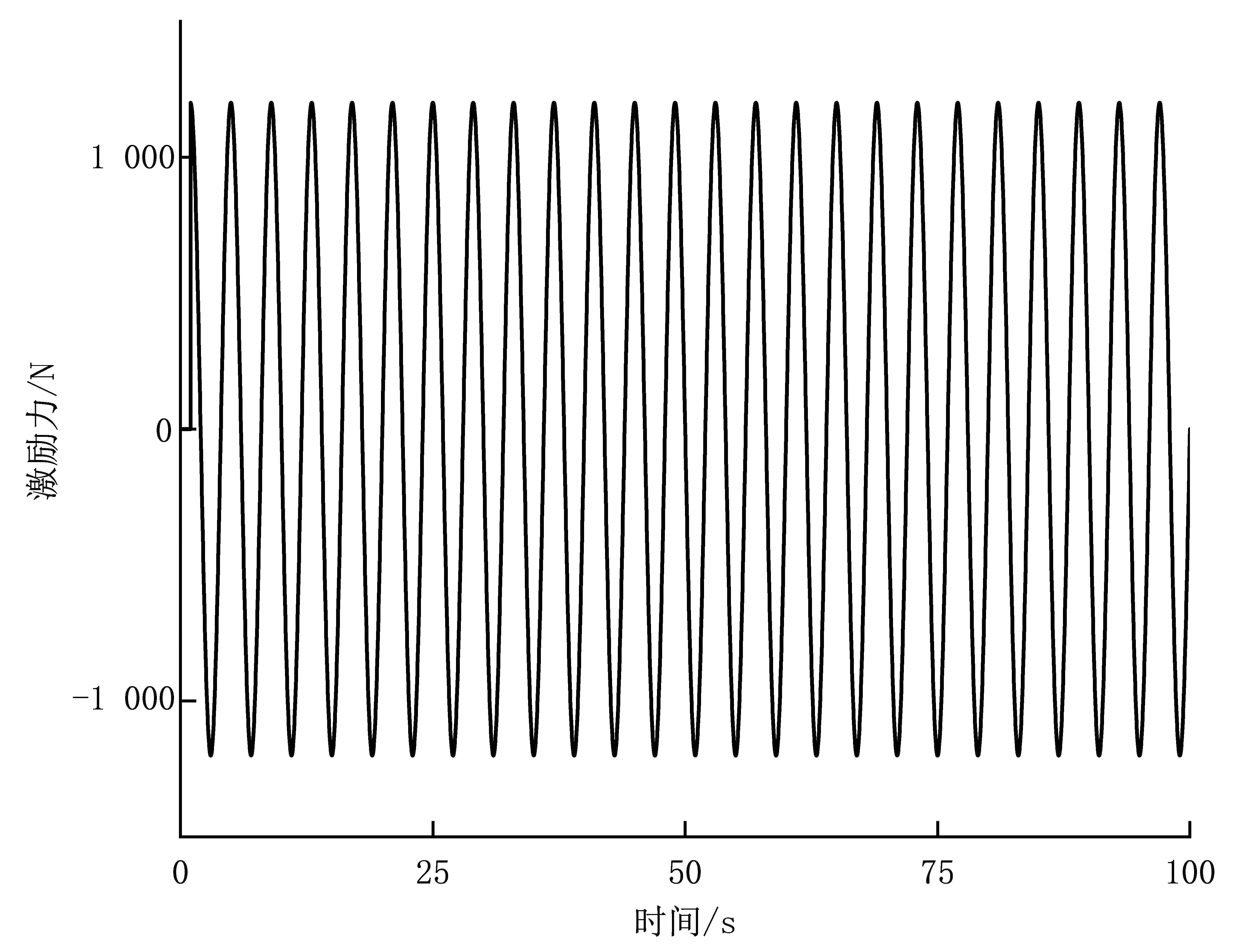
(a)海浪激励力曲线

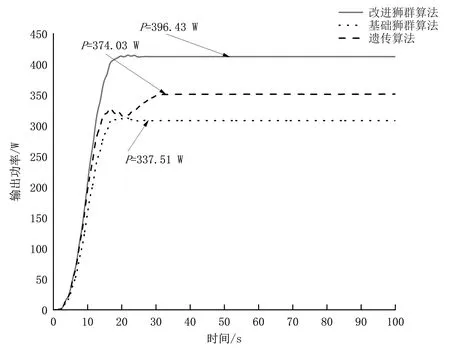
(b)输出功率曲线图4 规则海浪下的仿真Fig.4 Simulation under regular waves

由图4可知,在规则海浪的情况下,改进狮群算法、基础狮群算法和遗传算法分别在4个海浪周期、6个海浪周期和8个海浪周期时达到最大功率输出点,改进狮群算法的响应速度比基础狮群算法提高了0.5倍,比遗传算法提高了1倍。改进狮群算法、基础狮群算法和遗传算法的平均输出功率分别为396.43 W、337.51 W和374.03 W。由此可知,改进狮群算法的输出功率比基础狮群算法的输出功率高约17.46%,比遗传算法的输出功率高约5.99%。

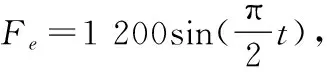
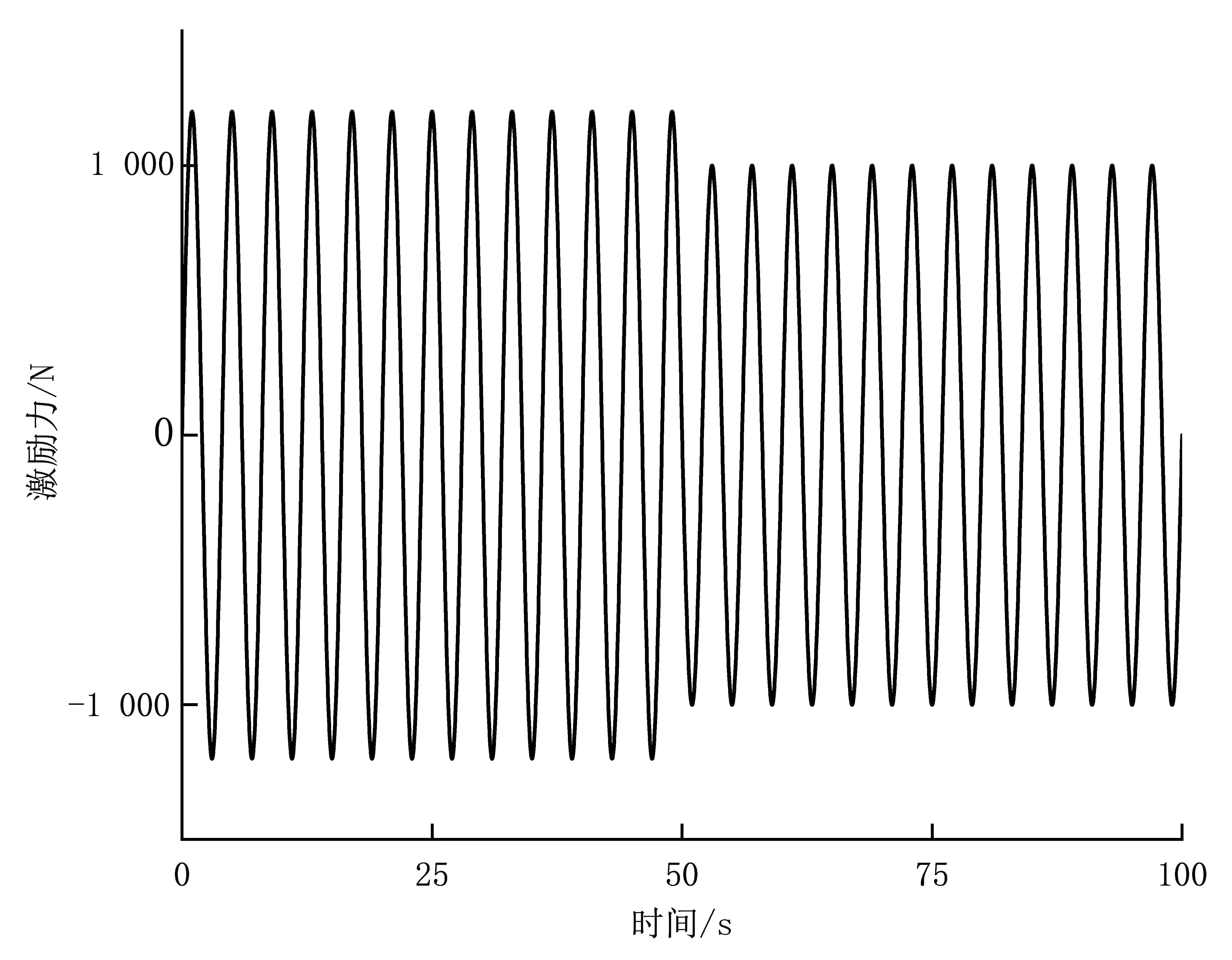
(a)海浪激励力变化曲线

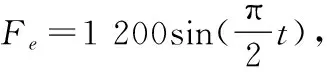
由图5和图6 可知,当模拟海浪条件发生变化后,改进狮群算法相比基础狮群算法和遗传算法,仍能够维持较高的功率输出。

根据非规则海浪的叠加原理,通过仿真得到非规则的海浪激励力,则发电系统在非规则海浪情况下的输出功率的仿真结果如图7所示。

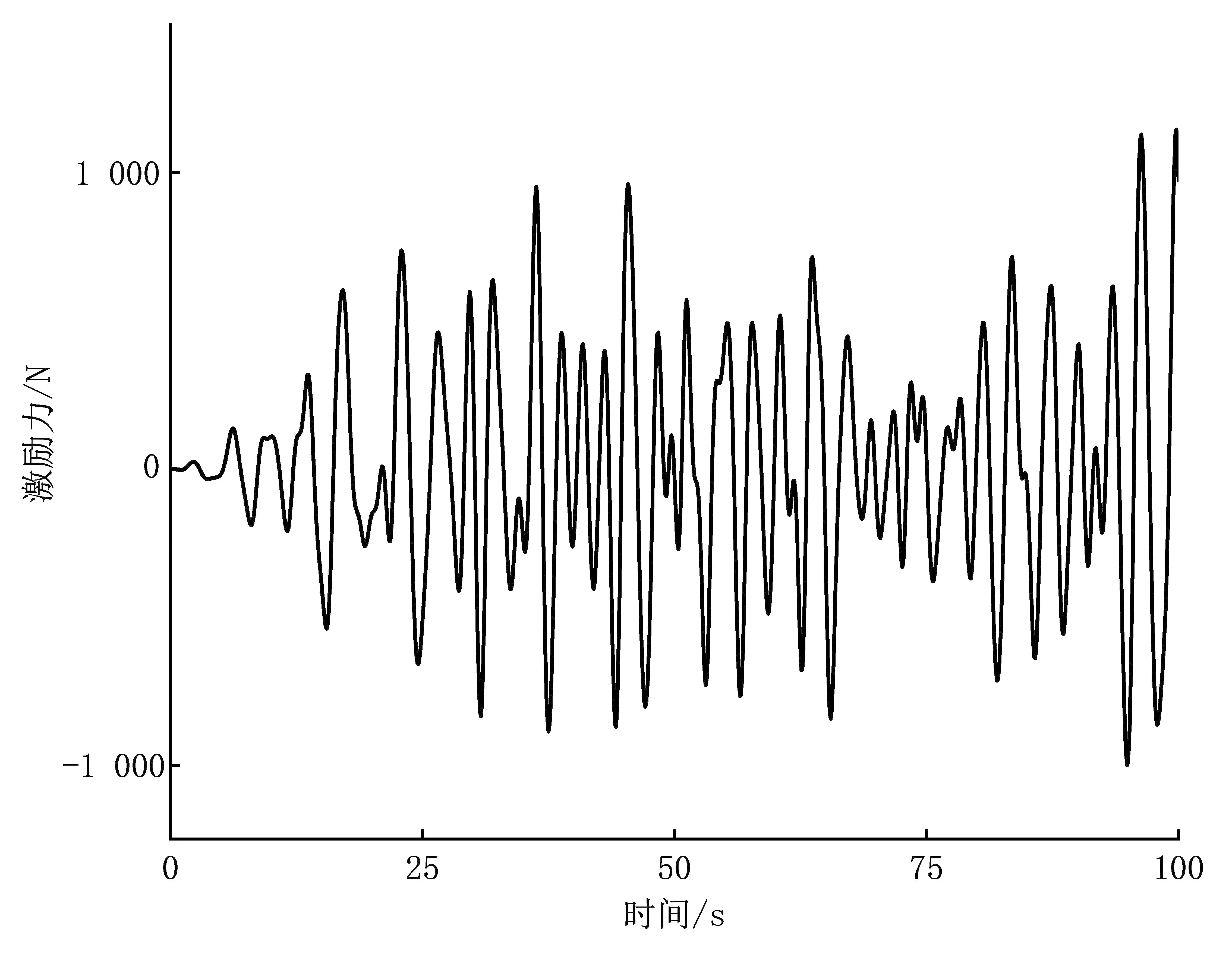
(a)非规则海浪激励力

由图7可知,采用改进狮群算法的最大功率跟踪点的跟踪效果明显要好于其他两种算法,采用改进狮群算法的平均输出功率为72.79 W,而采用遗传算法和基础狮群算法的平均功率分别为61.61 W和59.10 W。可以看出,改进狮群算法比遗传算法的能量捕获率提升了约18.15%,比基础狮群算法提升了约23.16%。

4 结论(Conclusion)

本文对直驱式波浪发电系统进行建模,针对直驱式波浪发电系统在实际海域中输出功率低的问题,提出引入Tent混沌映射、差分进化算法和灰狼优化算法的捕猎机制的改进狮群算法,并通过仿真和对比,得出以下结论:在规则海浪情况下,改进狮群算法的能量捕获率比遗传算法的能量捕获率高约5.99%,比基础狮群的能量捕获率高约17.46%。在非规则海浪的条件下,改进狮群算法比遗传算法的能量捕获率提高了约18.15%,比基础狮群算法的能量捕获率提高了约23.16%。结论证明提出的改进狮群算法可以有效地提高波浪发电系统在实际海浪中的输出功率。