采用功率同步控制的构网型换流器并网暂态同步稳定研究

项中明，倪秋龙，李振华，徐建平，李斯迅，张哲任，徐政

（1.国网浙江省电力有限公司，杭州 310007；2.国网浙江省电力有限公司金华供电公司，浙江 金华 321017；3.浙江大学 电气工程学院，杭州 310027）

0 引言

目前，电力系统正处于向“双高”（高比例可再生能源和高比例电力电子化）转型的关键阶段。非同步机电源的接入将打破传统同步发电机的主导地位，深刻影响电力系统的动态特性［1-6］。VSCHVDC（电压源换流器型高压直流输电）在大规模新能源并网中具有广泛的应用前景［7-12］。采用PSC（功率同步控制）的构网型换流器控制策略是VSC-HVDC的主要实现方式［7］，在弱电网下依然能与电网保持同步［13］，在“双高”系统中应用潜力巨大。

采用PSC的构网型换流器的控制结构与虚拟同步机本质相同［3］，其并入交流电网后的暂态同步稳定性近年来受到了学界的广泛关注。以往大量的文献采用在工作点线性化的小信号分析方法对构网型换流器的小干扰稳定性展开研究［11-15］，然而当电网发生严重故障时，构网型换流器的工作点将发生改变，此时小干扰分析方法对暂态稳定研究不再适用。因此，文献［16］采用相图曲线的方法研究了采用一阶PSC的构网型换流器在不同类型电网故障下的暂态行为；文献［17］与文献［18］分别基于李雅普诺夫方法与传统交流电力系统分析方法研究了采用PSC的构网型换流器的失稳机理，然而其未考虑电压变化对换流器暂态稳定性的耦合影响。针对此问题，文献［19-20］建立了考虑电压耦合后采用PSC的构网型换流器暂态稳定模型，文献［19］研究了换流器虚拟惯性与虚拟阻尼对暂态稳定性的影响，文献［20］研究了换流器电流限幅环节对暂态稳定性的影响。然而，文献［19-20］均没有考虑到故障切除的情景，而实际电网中故障通常在继电保护装置动作后得到切除。另外，已有文献所提出的暂态稳定性增强措施均存在一定缺陷，如文献［17-18］提出故障时直接改变有功功率给定值的增强方法，但没有提出能够准确识别故障的机制；文献［20］所提出的混合同步控制原理实际上引入了PLL（以锁相环）来改变PSC控制结构，使得控制结构复杂程度大大增加。

本文研究采用PSC的构网型换流器的并网暂态同步稳定机理。首先，建立了采用PSC的构网型换流器并网暂态稳定模型。随后，基于相图曲线研究了换流器在电网故障期间的暂态稳定性以及电压变化对换流器暂态稳定性的耦合影响。最后，基于电压的耦合作用，提出了通过改进PSC结构以改善换流器暂态稳定性的增强措施。

1 构网型换流器并网系统的数学模型

1.1 系统结构及控制策略

本文研究的换流器并网小系统模型如图1所示。其中VSC-HVDC接入电网的一端为采用PSC的构网型换流器，直流电压由远端换流器控制，可认为电网故障期间VSC（电压源换流器）的直流侧电压始终保持恒定［21］；is和us分别为换流站注入电网电流和PCC（公共连接点）交流母线电压，Ps+jQs表示构网型换流器向交流电网注入的功率。交流电网采用戴维南等效电路来模拟，ug为交流电网电压，Rs和Xs分别表示交流电网等值阻抗Zs的电阻、电抗分量。XT表示构网型换流器的连接变压器漏抗。

图1 VSC-HVDC并网系统模型Fig.1 VSC-HVDC grid-connected system model

本文采用的PSC控制策略与文献［13］相同。采用PSC的构网型换流器可以将换流器模拟成一台同步发电机，其控制目标是图1中的us，即对PCC点的交流电压幅值和相角进行控制。PSC是采用PSL（功率同步环）实现与电网电源同步。

PSL模拟了同步发电机的功角摇摆方程，其结构如图2所示［11］。图2中δs和ωs分别为换流器PCC点交流电压的功角和角速度，ω0为交流电网电压的角速度，一般取工频50 Hz；us，abc和is，abc分别为静止坐标系下PCC点交流电压和交流电流，us，dq和is，dq则是us，abc和is，abc在同步旋转坐标系下的分量（在d、q轴上的分量为usd、usq、isd、isq）；Ps*和Ps分别为换流器输出有功功率指令值与实际值，Jp和Dp分别为PSL仿照传统同步发电机设计的惯性系数与阻尼系数。Jp和Dp使得换流器能够更好地对交流系统起到惯性支撑的作用［22］。

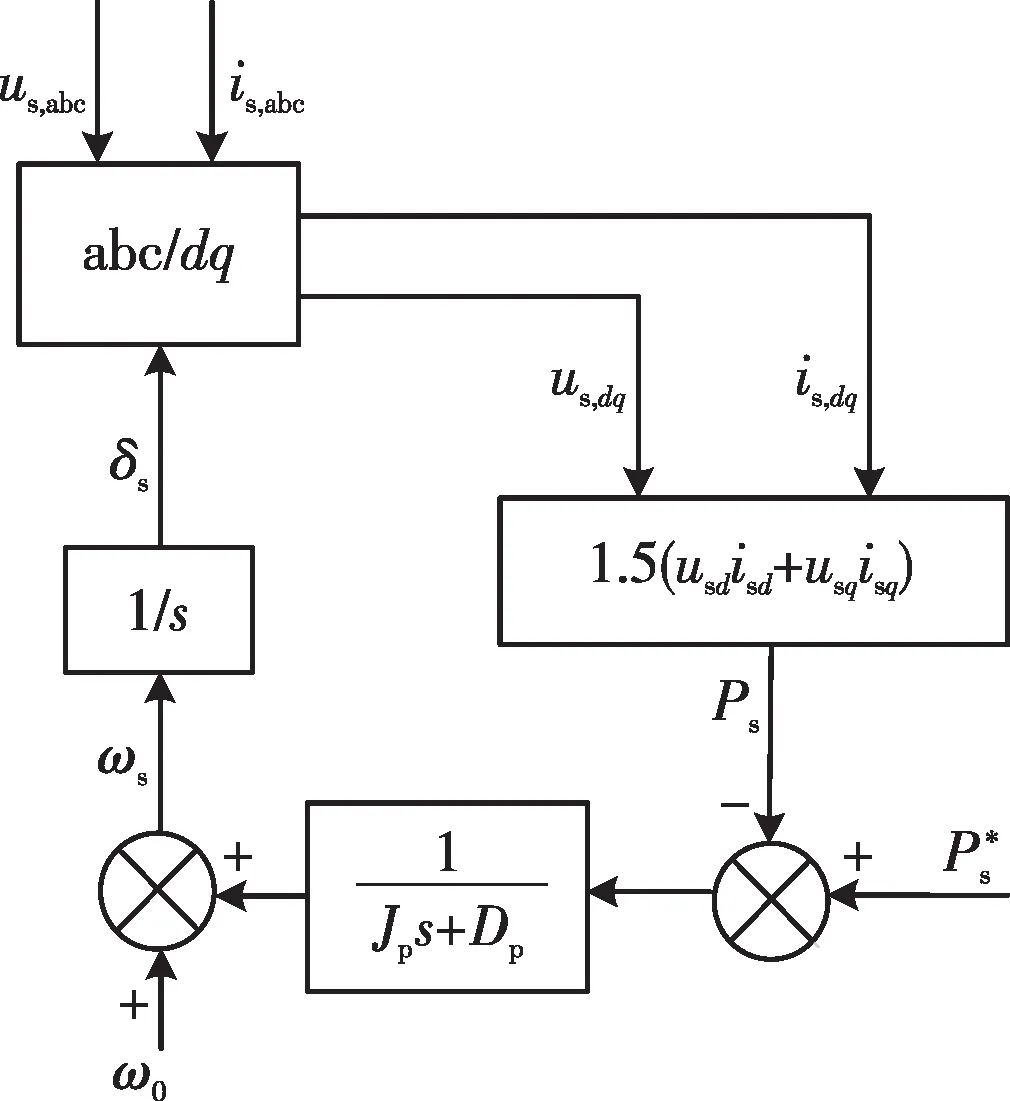
图2 PSL控制框图Fig.2 Block diagram of PSL control

根据图2，PSL的功角摇摆方程可用下式表示：

式中：ω为换流器PCC电压相对于交流电网电压的虚拟角速度。

结合式（1）与式（2），可知构网型换流器Ps与δs的关系可用下式表示：

电压外环控制器的结构如图3所示［13］，虚线框中的无功-电压环具有类似于同步电机励磁调节器的功能。图3中，Q*s和Qs分别为换流器输出无功功率指令值与实际值；V0和Vs分别为换流器PCC点电压有效值的指令值与实际值；u*sd、usd、、usq分别为PCC电压d轴分量与q轴分量的指令值与实际值；i*vd和i*vq分别为换流器d轴电流与q轴电流的指令值；Jq和Dq为无功电压环的控制参数［13］。

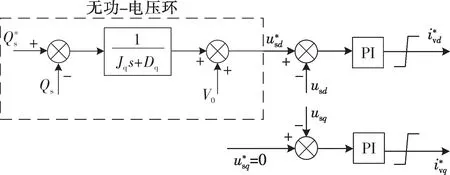
图3 电压外环控制器框图Fig.3 Block diagram of voltage outer loop controller

对于无功电压环，Vs与Qs的关系为可用下式表示：

1.2 构网型换流器并网暂态稳定模型

由于构网型换流器内环电流控制器的时间尺度（ms级）远小于控制外环的时间尺度［15］，因此在暂态稳定分析中忽略内环控制器动态特性，将构网型换流器视为可控电压源，其PCC点电压可用Vs∠δs描述。在此假设条件下，建立采用PSC的构网型换流器并网暂态稳定模型。交流系统的短路比ρSCR能够用来衡量系统强度［13］，其与系统阻抗的关系为：

式中：Zs为系统阻抗；φZ为系统阻抗角。

在高压电网中，系统阻抗角可近似认为是90°，即系统电阻Rs忽略不计。根据图1可计算出换流器注入交流系统的有功功率和无功功率分别为：

式中：Vg和δg分别为交流电网电压的幅值与功角。定义换流器PCC电压与交流电网电压间的角度差为虚拟功角δ=δs-δg，可以将式（7）、式（8）简化为：

将代表功率同步控制方程的式（3）、式（4）与代表构网型换流器并网功率方程的式（9）、式（10）联立，可以得出采用PSC的构网型换流器暂态稳定模型，如图4所示。

图4 构网型换流器暂态稳定模型Fig.4 Transient stability model of grid-forming converter

图4中功角-功率计算模块与电压幅值-无功计算模块分别由式（9）与式（10）计算得出，从图4可以看出，采用PSC的构网型换流器中P-δ功率同步环与Q-V无功电压控制之间通过换流器并网功率方程相互耦合。通过图4所示的暂态稳定模型可以定量研究采用PSC的构网型换流器并网系统暂态同步稳定性。

2 暂态稳定机理分析

2.1 PSL暂态稳定机理分析

为探究PSL暂态同步稳定机理，先不考虑电压变化的耦合作用，即认为换流器PCC点电压幅值Vs恒等于V0。此时换流器暂态稳定完全由有功功率-虚拟功角（P-δ）的暂态过程决定。将式（3）与式（7）联立，可以得到换流器有功功率-虚拟功角之间的动态关系如下式所示：

式中：令换流器的等效机械功率Pm=Ps*；换流器的等效电磁功率Pe=Ps=（VsVg/Xs）sinδ；换流器角速度Dp（dδ/dt）代表阻尼转矩［23］。

根据式（11）可知，PSL暂态同步稳定机理与传统同步发电机类似。在机理分析中，认为第一摇摆周期失稳即代表换流器发生暂态失稳。故障前，换流器并网系统稳定运行，此时δ=δ0，Pm=Pe，系统状态处于SEP（稳定平衡点）；故障期间，电网电压跌落，Pm＞Pe，虚拟功角前摆；当故障清除，电网电压恢复，Pm＜Pe，虚拟功角回摆。如果虚拟功角前摆越过UEP（不稳定平衡点），系统将暂态失稳。此外，换流器还受到阻尼作用的影响。

为了详细分析PSL的暂态稳定机理，采用相图曲线方法，根据式（11）绘制电网电压跌落故障下的换流器并网系统δ-ω相图曲线。通过相图曲线方法可以明显得出ω随δ变化关系，并且快速得出不同故障清除角下PSL暂态响应特性［19］。系统参数如表1所示，故障前δ=δ0=41°，ω=0，故障后Vg跌落至0.5 p.u.，故障持续时间不同时所得到的相图曲线如图5所示。

表1 系统参数Table 1 System parameters

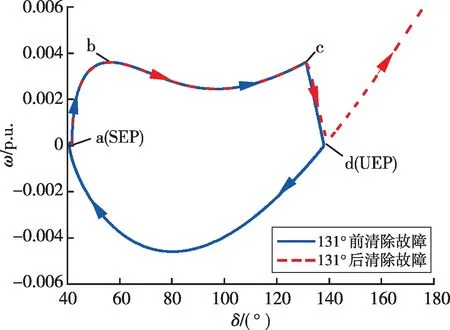
图5 PSL相图曲线Fig.5 Phase diagram curves of PSL

由图5可以看出，故障前系统工作在SEP点a，故障后电网电压跌落，换流器等效电磁功率大幅减小，Pe＜Pm，使得虚拟角速度快速上升，虚拟功角δ加速前摆，系统运行至点b。随后受阻尼作用影响，虚拟角速度适度减小。故障期间δ持续前摆，到达工作点c处故障清除，Pe＞Pm，换流器由于惯性作减速前摆，之后可以分为两种情况：

1）当δ前摆到CCA（故障极限清除角）［23］之后清除故障，故障清除时δ距离UEP较近。当电网电压恢复后，由于减速面积不足，δ越过UEP加速前摆，系统暂态失稳。

2）当δ前摆到CCA之前清除故障，故障清除时δ距离UEP较远。当电网电压恢复后，由于减速面积足够，δ在工作点d处角速度减为0并开始回摆。系统最终稳定在故障前SEP。

通过相图曲线方法快速得出不同故障清除角下系统的暂态响应特性，对于本算例系统，发现在功角前摆到131°前清除故障，系统恢复稳定；在功角前摆到131°后清除故障，系统失稳。因此确定CCA为131°。

根据上述分析，PSL的暂态稳定取决于系统在故障清除后是否具有充足的减速面积，也就是故障清除时的虚拟功角距离UEP是否有足够的裕度。而UEP对应的虚拟功角需要满足关系：

式中：最大功角δmax由换流器输出功率指令值P*s与实际值Ps的相对关系决定。

由式（12）可知，故障期间，如果Ps远小于P*s，δmax较小，虚拟功角将因减速面积不足而越过UEP，系统暂态失稳；如果Ps与P*s相差不大，δmax较大，虚拟功角将因减速面积充足而不会越过UEP，系统暂态稳定。通过式（12）计算得出，上例中UEP处δmax=141°。

2.2 电压变化耦合作用分析

故障发生后，换流器PCC电压Vs将快速跌落，换流器等效电磁功率可以表示为：

式中：Vs'为故障前PCC电压幅值；ΔVs为故障后PCC电压跌落值。

根据式（13），故障期间PCC电压跌落将进一步减小等效电磁功率。根据式（12），Vs减小使得δmax减小，进一步导致CCA减小，不利于系统暂态稳定性。

考虑电压变化的耦合作用后，换流器并网系统暂态稳定由功角-有功功率与电压幅值-无功功率共同决定。将式（4）与式（10）联立，PCC电压幅值-无功功率之间的动态关系如下式所示：

式（14）为描述并网系统无功平衡的微分方程，方程左侧主要由三部分构成：Vs变化率分量、无功分量Qs以及Vs偏离指令值的阻尼分量。当并网系统处于稳态时，Vs=V0且变化率为0，此时式（14）转化为式（10）。由式（14）可以看出，当其他条件不变时，δ前摆，cosδ减小，为满足式（14）平衡，Vs也应该减小；反之，δ回摆，cosδ增加，则Vs也应该上升。

式（11）与式（14）构成二阶微分方程组，利用MATLAB中的ode45函数可以求出其数值解，得到换流器并网系统的δ-ω相图曲线。系统参数如表1所示，换流器故障前虚拟功角初始值为41°，故障后电压跌落至0.5 p.u.。故障清除时间不同时得到相图曲线如图6所示。

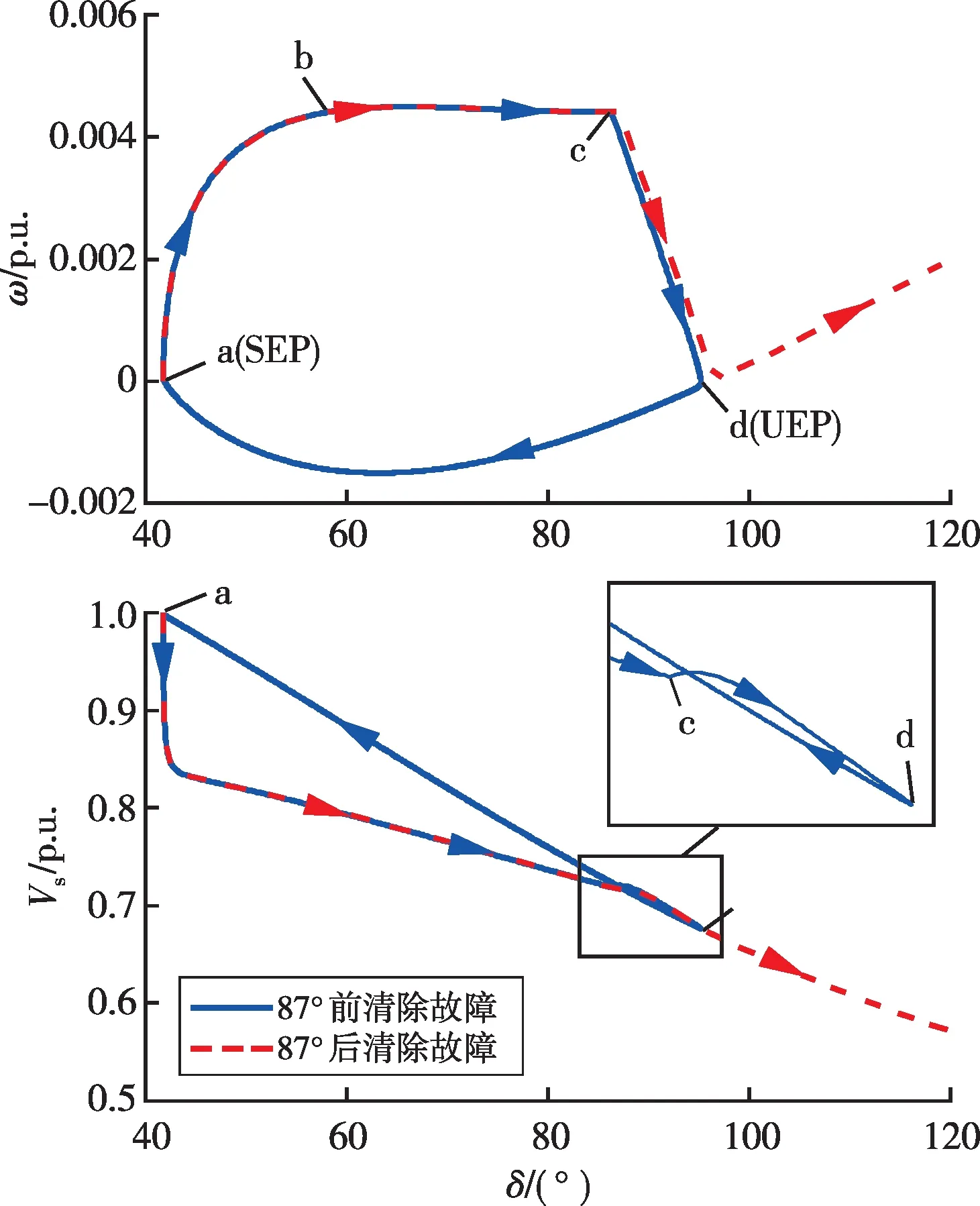
图6 考虑电压耦合后相图曲线Fig.6 Phase diagram curves with voltage coupling considered

图6展示了故障后Vs与虚拟功角的关系，可以看出，电网故障后PCC电压幅值Vs首先跟随Vg瞬时跌落，随后由于δ前摆，Vs逐渐跌落。故障清除时系统处于工作点c，Vs=0.7 p.u.。电网电压恢复后，Vs有一定程度的上升。随后δ由于惯性继续前摆，Vs出现短暂下跌。之后可以分为两种情况：

1）当虚拟功角前摆到CCA前清除故障，系统减速面积充足，δ到达工作点d时ω=0，之后Vs跟随δ回摆逐渐上升。并网系统最终恢复到故障前SEP。通过相图曲线方法得出该工况CCA为87°。

2）当虚拟功角前摆到CCA（87°）后清除故障，系统减速面积不足，δ越过UEP继续前摆，Vs跟随δ前摆继续减小。并网系统暂态失稳。

由图6可以看出，考虑无功电压耦合后，CCA明显减小。电网故障期间电网电压与PCC电压均会跌落，根据式（12），UEP处δmax大约在109°。CCA与UEP均明显减小，说明了无功电压耦合将会减小换流器并网系统的稳定裕度，不利于暂态同步稳定性。

3 暂态稳定增强控制策略

根据上文的分析可知：采用PSC的构网型换流器并网系统发生暂态失稳主要由于故障清除后减速面积相对不足，虚拟功角继续前摆越过UEP所导致。另外，故障期间PCC电压跌落与虚拟功角前摆基本同步。

对此提出相应的解决思路为：电网故障期间在PSL环节中引入电压幅值的负反馈镇定支路，以提高换流器暂态同步稳定性。具体的改进措施为：将PCC电压测量值低于指令值0.9倍作为电网故障判据。当Vs＜0.9V0时换流器认为电网故障，在PSL中接入负反馈镇定支路来调节功率给定值，其中反馈量为PCC电压指令值与测量值的偏差。当故障清除后，PCC电压恢复到正常水平，负反馈支路不再接入PSL，系统恢复到故障前的稳定工作点。改进后的PSL控制框图如图7所示。

图7 改进后的PSL控制框图Fig.7 Block diagram of improved PSL control

由图7可以看出，负反馈镇定支路只在电网故障期间接入PSL，因此采用本文提出的改进措施不会使得系统偏离正常工作点。改进后PSL的有功功率给定值P*s如下式所示：

式中：P*s，0为初始的功率给定值；Kq为电压偏差值反馈系数；V0和Vs分别为PCC电压额定值与实际测量值。

根据式（15），采用改进PSL后UEP处δmax需要满足的关系转换为：

由式（16）可以看出，引入电压偏差反馈量调节有功指令值，能够在电网故障期间有效减小换流器的等效机械功率，不仅能够在故障期间减小加速面积，还能在故障清除后增大UEP处的δmax，从而显著提升系统的暂态稳定裕度。

下面采用相图曲线的方法研究换流器并网系统的暂态同步稳定性。采用改进后PSL的构网型换流器的功角-有功功率可用下式表示：

将式（17）与式（14）联立，即可得到采用改进后PSL的构网型换流器的数学模型。分析当电网电压由1 p.u.跌落至0.5 p.u.时，Kq分别取0.5和0.8时暂态稳定增强的效果。系统参数如表1所示，换流器故障前功角初始值为41°，得到的相图曲线如图8所示。

图8 PSL改进后相图曲线Fig.8 Phase diagram curves of the improved PSL

由图8可以看出PSL改进后的并网系统UEP处δmax明显增大。Kq=0.5时，δmax=118.2°，CCA=112.9°；Kq=0.8时，δmax=135.6°，CCA=131.5°。PSL改进后的δmax与CCA均明显增大，说明故障期间引入电压偏差调节有功功率给定值能够有效增大并网系统的δmax与CCA，增强换流器并网系统的暂态稳定性。另外，Kq越大，故障期间加速面积越小，δmax越大，CCA越大。因此Kq越大，暂态稳定裕度越大，取Kq=0.8。

4 仿真分析

为了验证上述理论分析的正确性及暂态稳定增强控制策略的适用性，在时域仿真软件PSCAD/EMTDC中搭建采用PSC的构网型换流器并网小系统电磁暂态仿真模型，系统结构与图1一致。系统主回路参数及控制器参数如表1所示。改进后PSL中Kq=0.8。

4.1 电压跌落故障

当t=0.5 s时，电网电压幅值Vg由1 p.u.跌落至0.5 p.u.，故障分别持续0.1 s、0.2 s、0.3 s后清除，采用PSC的构网型换流器并网小系统暂态仿真结果如图9所示。

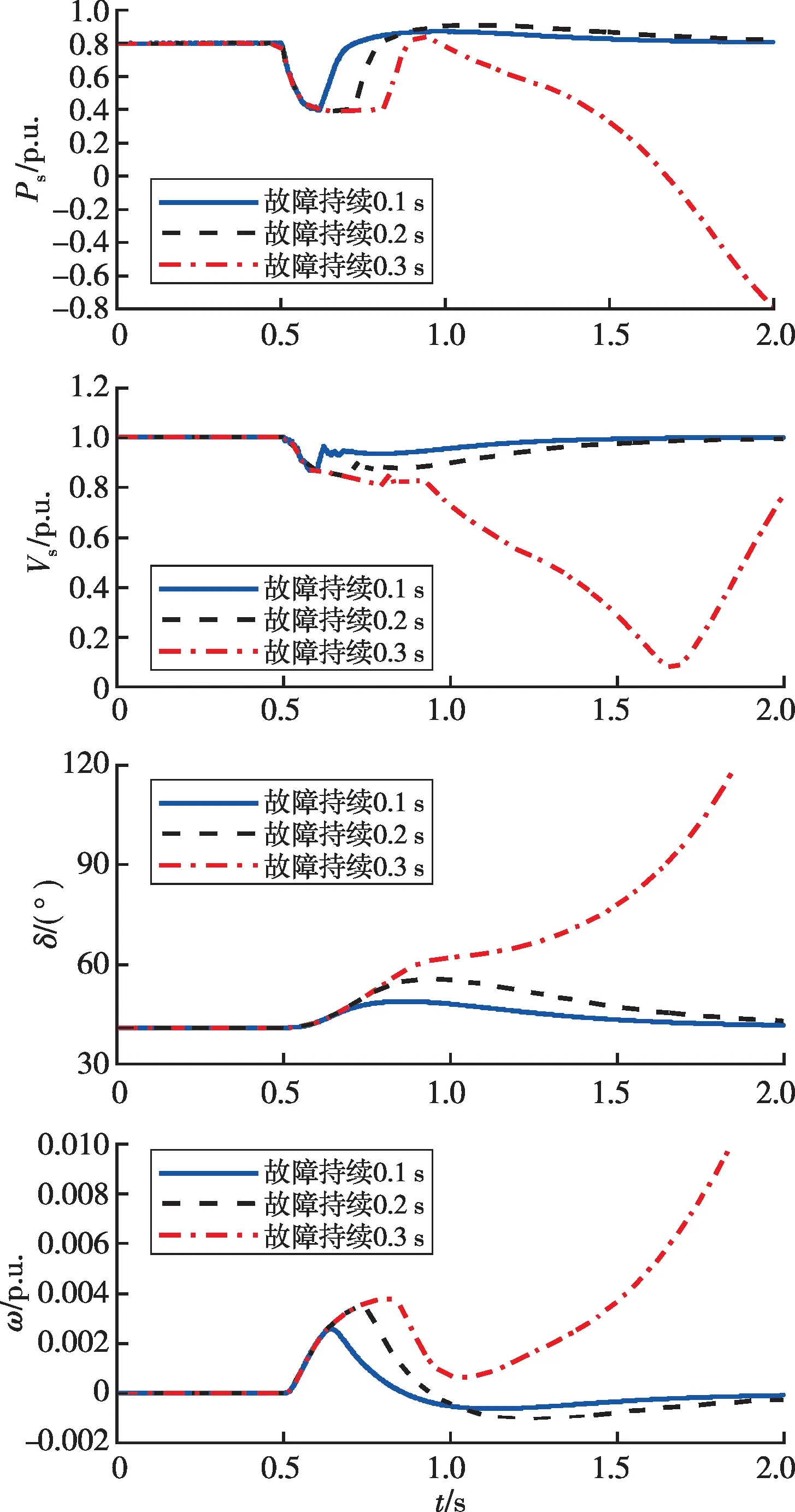
图9 换流器并网小系统电压跌落故障Fig.9 Voltage sag of the converter-connected small system

由图9可以看出，当电网电压Vg跌落至0.5 p.u.后，换流器输出Ps瞬时减小，换流器功角加速前摆，PCC电压持续下跌；故障清除后虚拟功角减速前摆，Vs跟随Vg有所恢复，随后Vs因为功角前摆继续下跌。若故障持续0.1 s、0.2 s后清除，角速度在到达UEP之前减为0，虚拟功角回摆，系统恢复暂态稳定；若故障持续0.3 s后清除，虚拟角速度在到达UEP时没有减为0，虚拟功角越过UEP继续前摆，系统暂态失稳。换流器暂态稳定仿真结果与第二章中根据相图曲线分析所得结果基本一致，证明了本文所提出的暂态稳定模型的准确性。

当t=0.5 s时，电网电压幅值Vg由1 p.u.跌落至0.5 p.u.，故障分别持续0.2 s、0.3 s、0.4 s后清除，PSL改进后的构网型换流器并网小系统暂态仿真结果如图10所示。由图10可以看出，PSL改进后系统故障响应特性与PSL改进前相似，但相同故障条件下PSL改进后换流器的角速度明显减小，故障分别持续0.3 s与0.4 s时换流器均能在故障清除后与电网恢复同步运行，说明本文所提出的PSL改进策略能够有效增强构网型换流器的暂态同步稳定性。

图10 PSL改进后换流器小并网系统电压跌落故障Fig.10 Voltage sag of the converter-connected small system with PSL improved

4.2 三相短路故障

为了进一步证明暂态稳定机理分析的正确性，仿真研究三相短路故障下换流器暂态失稳特性。当t=0.5 s时，换流器并网线路中点处发生三相短路故障，故障电阻为0.1 Ω，故障分别持续0.1 s、0.2 s后清除，采用PSC的构网型换流器并网系统暂态仿真结果如图11所示。

图11 换流器并网系统三相短路故障Fig.11 Three-phase short-circuit fault in converterconnected system

由图11可以看出，三相短路故障发生后，PCC电压瞬时跌落，换流器功角加速前摆。如果故障较早清除，角速度在到达UEP之前减为0，功角回摆，系统恢复稳定；如果故障持续时间为0.2 s，虚拟功角越过UEP继续前摆，电压持续跌落，系统暂态失稳。三相短路故障下构网型换流器并网系统暂态失稳特征与电压跌落故障下基本一致。

当t=0.5 s时，换流器并网线路中点处发生三相短路故障，故障电阻为0.1 Ω，故障分别持续0.2 s、0.3 s后清除，PSL改进后的构网型换流器并网系统暂态仿真结果如图12所示。

图12 PSL改进后换流器并网系统三相短路故障Fig.12 Three-phase short-circuit fault in converterconnected system with PSL improved

由图12可以看出，改进后PSL的并网系统暂态稳定性明显增强。当故障持续时间分别为0.2 s、0.3 s时，系统均能够在故障清除后恢复暂态稳定，说明本文提出的控制方法能够有效增强采用PSC的构网型换流器在三相短路故障下的暂态稳定性。

4.3 某市实际电网算例

为了进一步验证采用PSC的构网型换流器并网暂态同步稳定机理的正确性与适用性，在PSCAD/EMTDC中搭建如图13所示的某市实际电网的等值交流系统电磁暂态仿真模型，研究实际电网场景下换流器暂态失稳特性。其中主网架选取500 kV以上电压等级的节点。等值系统中同步机编号及参数见表2、表3，负荷参数见表4。一台构网型换流器通过WN站并网，构网型换流器采用功率同步控制策略，其参数见表5。

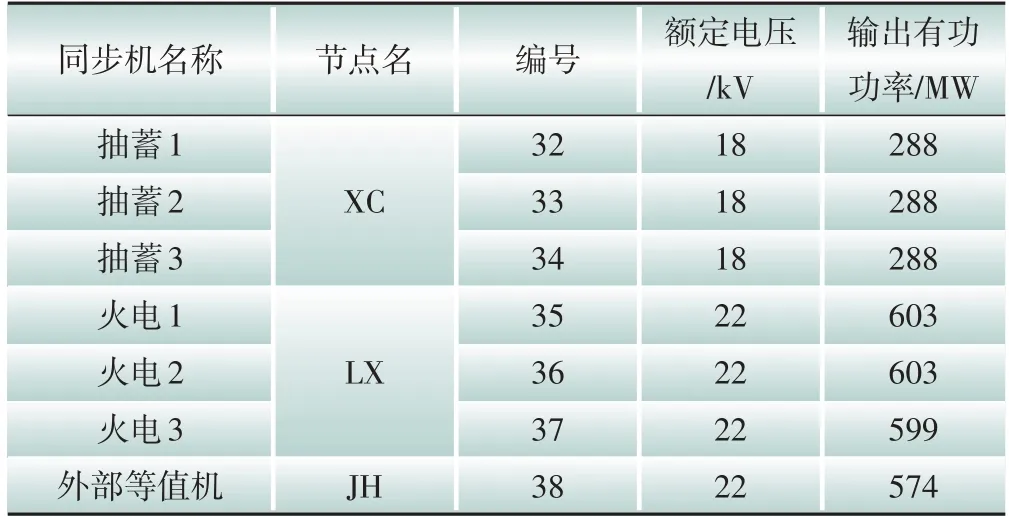
表2 同步机编号Table 2 Synchronizer number

表3 同步机参数Table 3 Synchronizer parameters

表4 负荷参数Table 4 Load parameters

表5 构网型换流器参数Table 5 Parameters of grid-forming converters

图13 某市电网等值拓扑Fig.13 Equivalent topology of a power grid in a city

当t=1 s时，换流器并网线路中点处发生三相短路故障，故障电阻为0.1 Ω，故障分别持续0.3 s、0.4 s后清除，实际电网场景下采用PSC的构网型。

换流器并网系统暂态仿真结果如图14所示，相同故障条件下，故障分别持续0.3 s、0.4 s、0.5 s后清除，PSL改进后的构网型换流器并网系统暂态仿真结果如图15所示。

图14 实际电网场景下三相短路故障Fig.14 Three-phase short-circuit fault in real grid scenario

图15 实际电网场景下PSL改进后三相短路故障Fig.15 Three-phase short-circuit fault with PSL improved in real grid scenario

由图14可以看出，在实际电网场景下，采用PSC的构网型换流器暂态失稳表现特征与之前的仿真结果保持一致。当故障持续时间为0.3 s时，虚拟角速度在到达UEP之前减为0，系统恢复暂态稳定；当故障持续时间为0.4 s时，虚拟功角前摆越过UEP，系统暂态失稳。

由图15可以看出，在实际电网场景下，本文提出的暂态稳定增强控制策略依然适用。当故障分别持续0.3 s、0.4 s、0.5 s后清除，PSL改进后的换流器并网系统均能够恢复暂态稳定。说明本文提出的PSL改进措施在实际电网场景下依然适用。

进一步地，用CCT（故障极限清除时间）表征暂态稳定性强弱［23］，仿真研究换流器并网小系统、换流器接入实际电网两种场景下发生三相短路故障，PSL改进前后对应的CCT仿真结果如表6所示。可以看出，两种场景下PSL改进后系统的CCT均明显增大，说明本文提出的控制方法能够有效增强构网型换流器的暂态同步稳定性。

表6 三相短路故障CCT仿真结果Table 6 CCT simulation results of three-phase shortcircuit fault

5 结论

本文研究了采用PSC的构网型换流器并网暂态同步稳定机理以及无功电压变化对暂态稳定性的影响，并提出了相应的暂态稳定增强控制策略，主要结论如下：

1）UEP可以通过δmax表示，电压变化的耦合作用将减小δmax，不利于换流器并网系统的暂态稳定，且故障后PCC电压跌落与功角前摆基本同步。

2）通过引入电压偏差反馈来调节PSL功率给定值，能够在故障期间减小等效机械功率，增大UEP处δmax，显著增强了换流器并网系统的暂态同步稳定性。