基于故障信息的风机并网系统暂态稳定分析方法

陈水耀，胡晨，马伟，王源涛，王嘉琦

（1.国网浙江省电力有限公司，杭州 310007；2.国网浙江省电力有限公司杭州供电公司，杭州 310009）

0 引言

随着风力发电技术的迅速发展，风电场并网规模日益增大。目前，我国风电场主要采用双馈异步电机，其物理特性及控制方式导致它的功角特性不同于传统同步发电机组，再加上风电场出力本身受天气影响具有随机性和波动性，大规模的风电并网势必给电力系统的暂态稳定运行带来更多不确定性［1-8］。因此，研究高比例、高密度风电接入下电力系统的暂态稳定分析方法具有非常重要的现实意义。

目前，国内外学者对含风电场电力系统的暂态稳定分析方法主要有时域仿真法［9-13］和直接法［14-17］。时域仿真法通常先对风电机组或风电场进行等值建模，再将模型融入电力系统中，通过仿真计算得到风电场容量、并网点位置以及控制类型等因素对系统暂态稳定性的影响。该方法精确考虑风电场的复杂动态模型，准确可靠，但对大电网而言，其计算时间长，仅能基于预想故障离线计算，不能给出稳定裕度的定量指标［18］。直接法通过用系统状态量表征的能量函数来评估系统是否失稳，可实现快速判断［19-22］，但该方法通常都只考虑了三相短路下系统的暂态稳定性，不适用于不对称短路。此外，现有方法在一定程度上忽视了继电保护在稳定性判断中的潜在作用。合理利用包含故障发生位置、故障接地阻抗等在内继电保护故障信息，可减少计算误差，提高稳定判断结果的准确性，为控制系统采取后续措施提供更可靠的依据。

针对上述问题，本文提出了一种基于故障信息的风机并网系统暂态稳定分析方法。首先，分析了故障后双馈风电场的对外特性以及负序、零序阻抗模型。然后，推导了包含故障信息的系统导纳收缩矩阵，并在此基础上利用EEAC（扩展等面积定则）提出一种暂态稳定裕度指标，作为系统是否发生暂态失稳的判断依据。最后，通过对含双馈风电场的3机9节点系统进行仿真，验证了所提方法的正确性和有效性。

1 双馈风电场对外特性及故障信息

1.1 双馈风电场等效外特性

以图1所示含双馈风电场的简单系统为例，对不对称短路故障下影响系统暂态稳定性的因素进行分析。

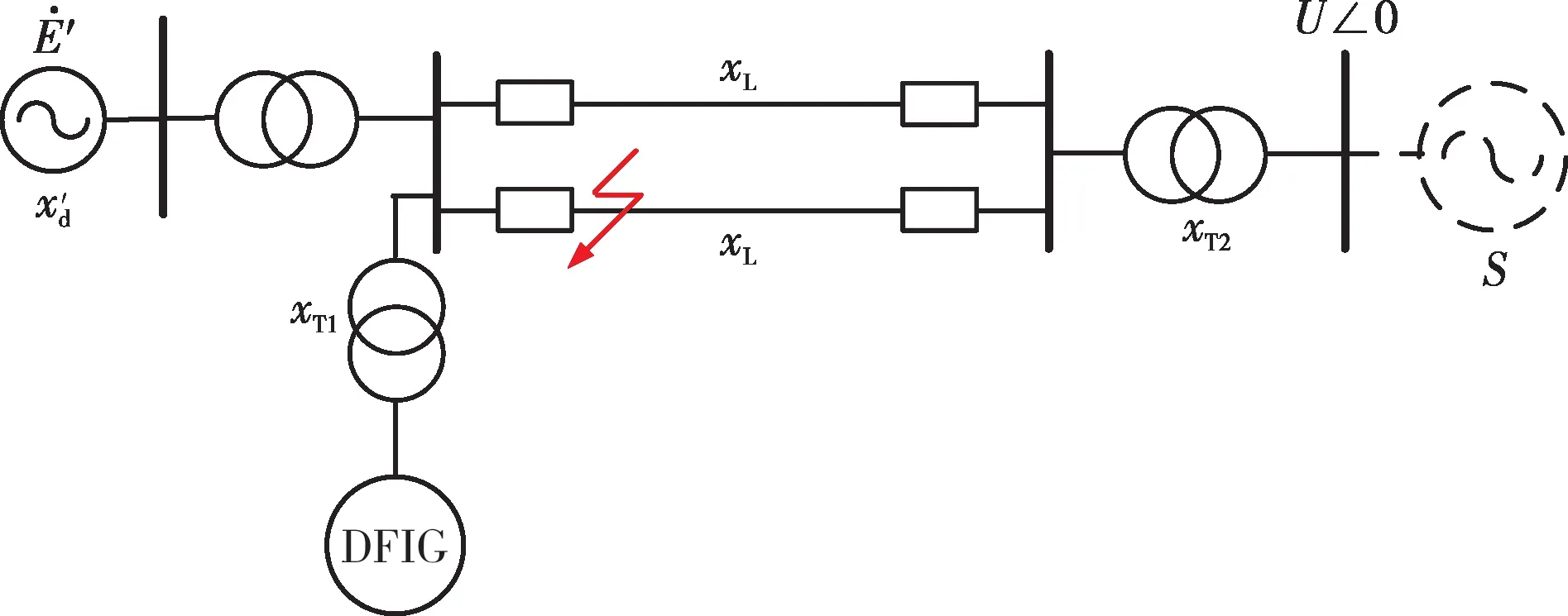
图1 含双馈风电场系统模型Fig.1 Model of a power sytem with doubly-fed wind farm

与同步发电机不同，DFIG（双馈感应发电机）依靠双变流器结构与矢量控制，使机械部分与电气部分的联系近似于解耦，因此双馈风电场本身不存在功角稳定问题，其对系统暂态稳定性的影响主要在于风电场接入后将引起系统的潮流发生变化，各同步机相连节点的节点电压幅值、相位以及电磁功率随之改变，进而改变整个系统内同步机功角之间的互同步性。

正常运行情况下，风电场一般运行在恒功率因数下，与电网间不存在无功交换。但当系统中发生短路故障导致风电场出口母线电压降落后，风电场按规定需向系统输出无功以提供电压支持，直至故障消除后，风电场又恢复恒功率因数运行。因此考虑风电场的功率特性，其在故障前及故障切除后可等效为一个负的接地电导g，在故障期间可等效为接地导纳y=g+jb。

式中：Pdfig、Qdfig、Udfig分别为DFIG输出的有功功率、无功功率和DFIG出口节点电压。

假设系统在母线出口处发生两相接地短路故障，故障期间系统等值电路如图2所示。其中，Zdfig.2为DFIG的负序阻抗，ZΔ为短路故障导致的网络附加阻抗，其在不同短路类型下的取值如表1所示。可知不对称短路故障下，ZΔ取值与短路点处的负序等值阻抗Z（2）、零序等值阻抗Z（0）以及故障接地阻抗（对两相相间短路故障为故障点短路阻抗）Zf有关。

表1 不同故障类型下ZΔ取值Table 1 Values of ZΔ under different faults

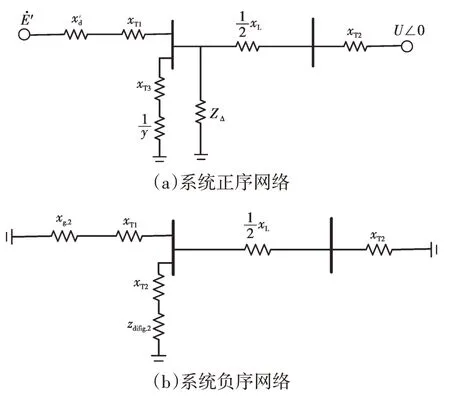
图2 不对称故障下系统等值电路Fig.2 Equivalent circuit of the system under an asymmetric fault

对于双馈风电场，其负序阻抗与故障后双馈风电机组采取的低电压穿越策略等有关，且随时间不断变化，难以给出定量的表达式。为解决该问题，可由风电场出口处的继电保护装置提取本地的负序电压Um.2和负序电流Im.2，按式（2）实时计算风电场的负序阻抗。

由于风电场主变高压侧中性点一般直接接地，其零序阻抗可视为零。

1.2 继电保护装置提供的故障信息

以图1所示系统为例，对影响系统暂态稳定性的因素进行分析。为简化分析过程，忽略双馈风电场支路，仅对常规单机无穷大系统进行分析。系统的功角摇摆方程如下：

式中：δ和ω分别为发电机的转子角和角频率；M为发电机惯量；Pm和Pemi分别为发电机的机械功率和电磁功率，i=1、2、3分别代表故障前、故障中和故障后三个阶段；xL.k为故障发生在位置k时的等效电抗。

利用等面积定则求得系统极限切除角δcm：

故障后系统保持暂态稳定的判断条件为：

式中：δc为系统实际切除角。

可知，影响系统暂态稳定的因素除了风电场等效导纳和负序阻抗以外，还包括故障发生位置k以及故障接地阻抗Zf。然而现有系统暂态稳定性分析方法往往忽略了后两者的影响，容易造成计算误差，使得判断结果可能保守或冒进。因此，将包含风电场等效导纳、风电场负序阻抗、故障发生位置以及故障接地阻抗在内的故障信息引入暂态稳定性判断中，对于提升判断结果的准确性有着重要作用，而这些信息恰好可以由继电保护装置提供。

自20世纪初至今，继电保护装置完成了从机电式保护、晶体管式保护到微机保护的过渡，目前微机保护己经成为静态继电保护装置的唯一形式［23］。微机保护不仅能精确地实现复杂的保护功能，还具有故障分析、故障定位和与调度计算机进行信息交换等功能，这为事故分析和利用故障信息进行调度控制提供了便利。凭借先进的故障分析和判别技术，微机保护处可提供的故障信息除直接测量得到的电气量如电压、电流和功率外还包括故障持续时间、故障类型、故障位置及接地电阻等重要信息［24］。

同时，随着智能电网建设不断推向深入，调度中心与变电站间的信息共享需求剧增，建立高速、双向、实时、集成的信息通道已成为必然趋势［25］。随着基于IEC 61850通信标准的智能化变电站的推广应用，同样为故障信息的传递提供了可能。以图3所示智能变电站架构为例，故障发生后，位于间隔层的继电保护装置通过接收合并单元处传递过来的电压和电流信息，经过计算分析，判断是否发生区内故障，并向智能终端发出断路器开、合闸指令，并将分析得到的故障持续时间和故障类型等故障信息通过交换机经由光纤网络传送至站内主机和调度中心，从而实现故障信息的共享。

图3 智能变电站架构Fig.3 Intelligent substation architecture

由于故障信息全程采用光纤作为信息通道，信息传输速度极快。故障发生后，继电保护装置动作时间约为20 ms，断路器动作时间约40 ms［26］，假设故障信息从继电保护装置到调度中心共经过4台交换机，光纤路径长度为1 000 km，则在网络无阻塞的情况下整个通信网络延时为：t=（每字节传输时间×最大报文长度+交换机结构延时）×交换机数＋光纤路径长度/光速［27］，得到t≈3.84 ms。则故障发生后各环节的时间节点如图4所示，可以看到从故障发生到继电保护装置将故障信息传递至调度中心仅需不到70 ms，这为调度中心利用故障信息进行电力系统稳定分析和紧急控制提供了可能。

图4 故障信息传递时间轴Fig.4 Timeline of fault information transfer

2 基于故障信息的系统暂态稳定性分析

多机系统中第i台发电机遭受扰动后的运动方程为：

式中：δi和ωi分别为发电机i的转子角和角频率；Mi为发电机i的惯量；Pmi和Pei分别为发电机i的机械功率和电磁功率。

式中：Ei和Ej分别为i、j点的电势；Gij、Bij、δij分别为节点i与j间等效电导、电纳和转子角。

由式（10）、式（11）可知，影响δi及ωi变化的变量为Pei和Pmi，其中与故障发生位置及故障接地阻抗等故障信息相关的只有Pei。

2.1 含故障信息的导纳收缩矩阵

为分析含双馈风电场电力系统的暂态稳定情况，先将网络节点导纳矩阵收缩至只含发电机节点、双馈风电场出口节点以及故障线路两端的两个节点。以图5所示系统为例，该系统节点总数为N，其中包含n个发电机节点、m个风电场节点，将故障线路两端节点设为n+1和n+2，Z为线路阻抗，则系统原始导纳阵可表示为：

图5 含双馈风电场系统网络示意图Fig.5 Schematic diagram of the power system with doublyfed wind farms

式中：g为发电机内节点，为方便后续分析，将故障线路两端节点也并入这一部分，w为风电场出口节点，e为上述节点以外的其他节点。

由前文分析，风电场在故障期间可等效为接地导纳，因此仅需将导纳阵中Yw，w部分的对角线元素yi，i按式（13）进行修改即可将风电场出口节点变为普通节点。

式中：yi为双馈风电场i的等效接地导纳。

按式（14）对导纳阵进行第一次收缩，仅留下发电机内节点及故障线路两端节点。

为便于分析，将Y'分割为以下形式：

不对称短路发生期间，相当于在故障点处增加一个接地的附加阻抗ZΔ，如图6（a）所示。为求ZΔ需要根据双馈风电场出口处继电保护装置测得的风电场负序阻抗信息，建立整个系统的负序网络和零序网络，从而求得短路点处的负序等值阻抗Z2及零序等值阻抗Z0，再根据故障线路上继电保护装置测得的接地阻抗Zf，即可按表1得到不同短路类型下对应的ZΔ。

图6 短路期间故障线路等值电路Fig.6 Equivalent circuit of a fault line during short circuit

短路发生后，导纳阵Y'中仅YD中的元素会发生变化，经过图6（b）所示的Y-Δ变换，故障前后YD中元素变化量如下：

式中：Z为线路阻抗。

故障后YD部分变为：

此时将导纳阵Y'进一步收缩至只含n个发电机节点，得到最终导纳阵。

其中：

此时Pei可改写为

式中：Pei.0的取值与k和ZΔ均无关，仅ΔPei部分随k和ZΔ变化。

2.2 基于故障信息的暂态稳定裕度算法

根据EEAC，将多机系统分解为临界机群Sg和其余机群Ag，先将两个机群等值为两机系统：

再将两机系统等值为单机无穷大系统：

式中：δg、Pmg、Peg分别为两机系统等值转子角、发电机的机械功率、发电机惯量和电磁功率；MT为所有的发电机的惯量之和；Mk为第k台发电机的惯量，属于等值过程的中间变量。

当得到各发电机功角轨迹后，对式（22）右端积分可求得加速面积Sac和减速面积Sde，需要注意Sac和Sdc分别是针对故障期间和故障线路切除后不平衡功率的积分，二者在计算Pei时使用的导纳阵不同，后者对应的导纳阵与k和Zf不再相关。

定义暂态稳定裕度V：

则针对某一故障切除时刻tc，V随变量k和Zf的变化情况可表示为图7所示的三维曲面，而曲面与平面V=0的交线即系统临界稳定所对应的（k，Zf）取值集合，相应的曲面在平面V=0上方和下方部分对应的（k，Zf）点分别为稳定点和非稳定点。

图7 V随k和Zf变化的三维曲面Fig.7 3D surface of V varying with k and Zf

3 算例仿真

为验证本文所提方法的有效性，对IEEE 3机9节点系统进行了改进，如图8所示。在原有系统的节点7处并入双馈风电场，风电场额定容量为50 MW。设置故障线路为L1，故障位置k的取值范围0～1，代表故障发生地点从母线5到母线7之间变化。

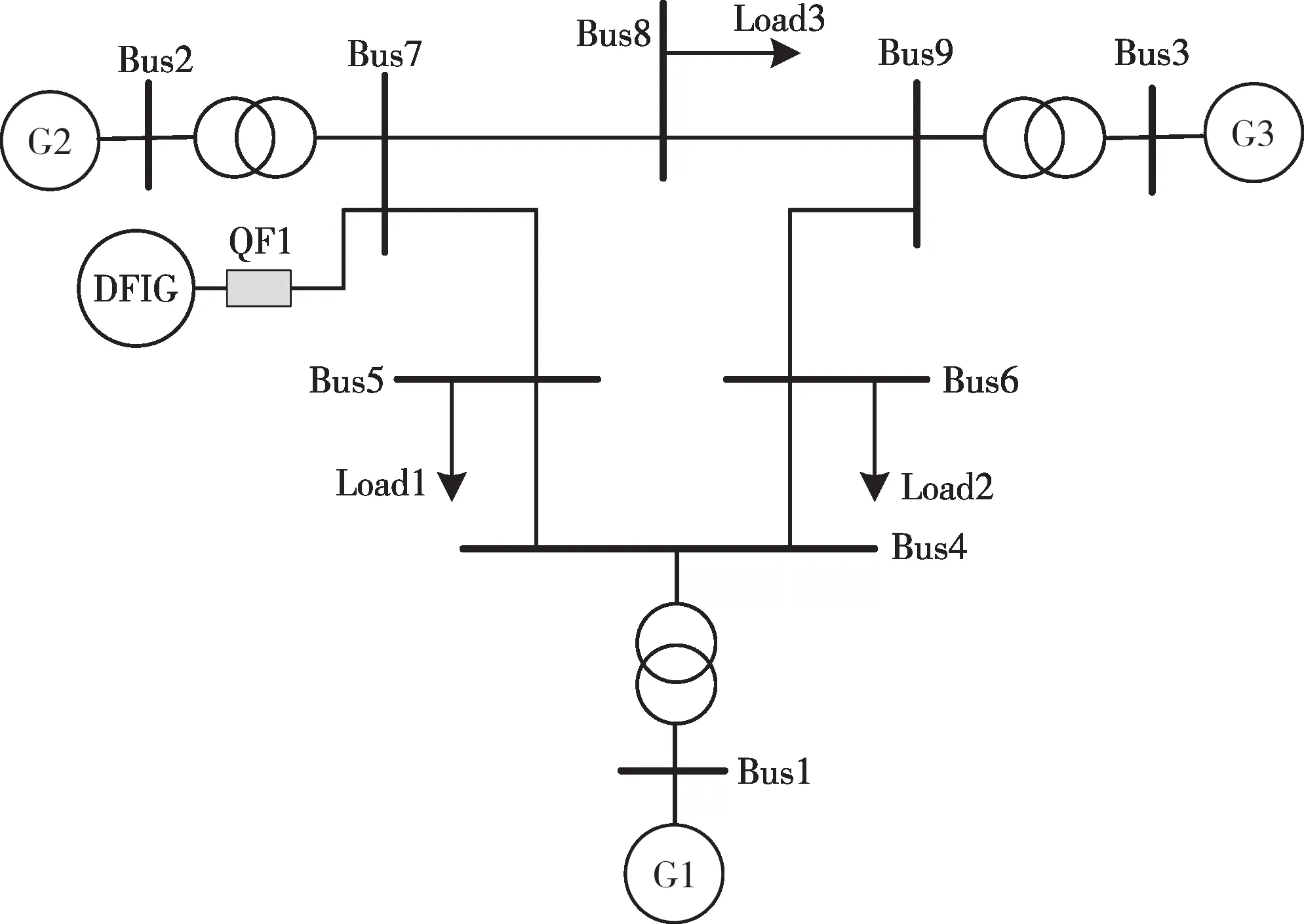
图8 含双馈风电场的3机9节点系统Fig.8 3-machine 9-node system with doubly-fed wind farms

为模拟双馈风电场出口处继电保护装置在故障期间测得的风电场负序阻抗。利用PSCAD软件对系统进行了建模仿真，通过对风电场出口处三相电压和电流的检测，得到不同故障类型下风电场负序阻抗如图9所示。可以看到，双馈风电场等效负序阻抗不仅随故障类型而变化，还与故障发生位置k有关。

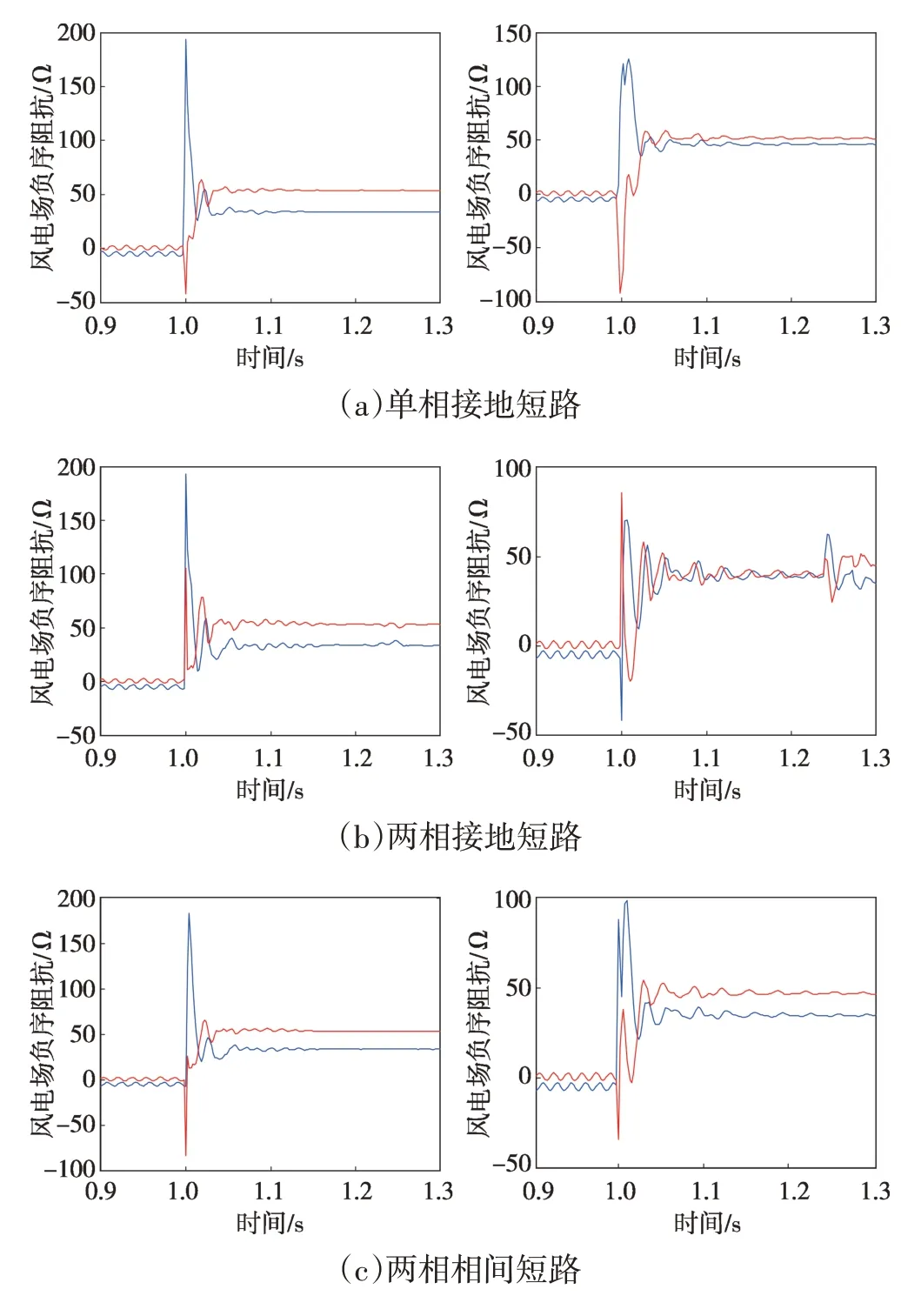
图9 不同故障类型下双馈风电场负序阻抗Fig.9 Negative-sequence impedance of a doubly-fed wind farm under different faults

根据得到的双馈风电场负序阻抗信息计算出网络附加阻抗XΔ，按上文方法求得不同短路类型下系统的导纳收缩矩阵，最终得到故障切除时间tc下的系统暂态稳定裕度V随故障位置k及接地阻抗Zf变化的二维曲面，如图10所示。可以发现在三种不对称短路故障下加入双馈风电场后系统的暂态稳定裕度均有不同程度的下降。此外，对于故障位置k，暂态稳定裕度随k的增大而逐渐减小，说明故障位置越靠近母线7，系统的暂态稳定性越差；而对于接地阻抗Zf，暂态稳定裕度随Zf的增大而增大，说明接地阻抗越大，对系统暂态稳定的威胁越小。

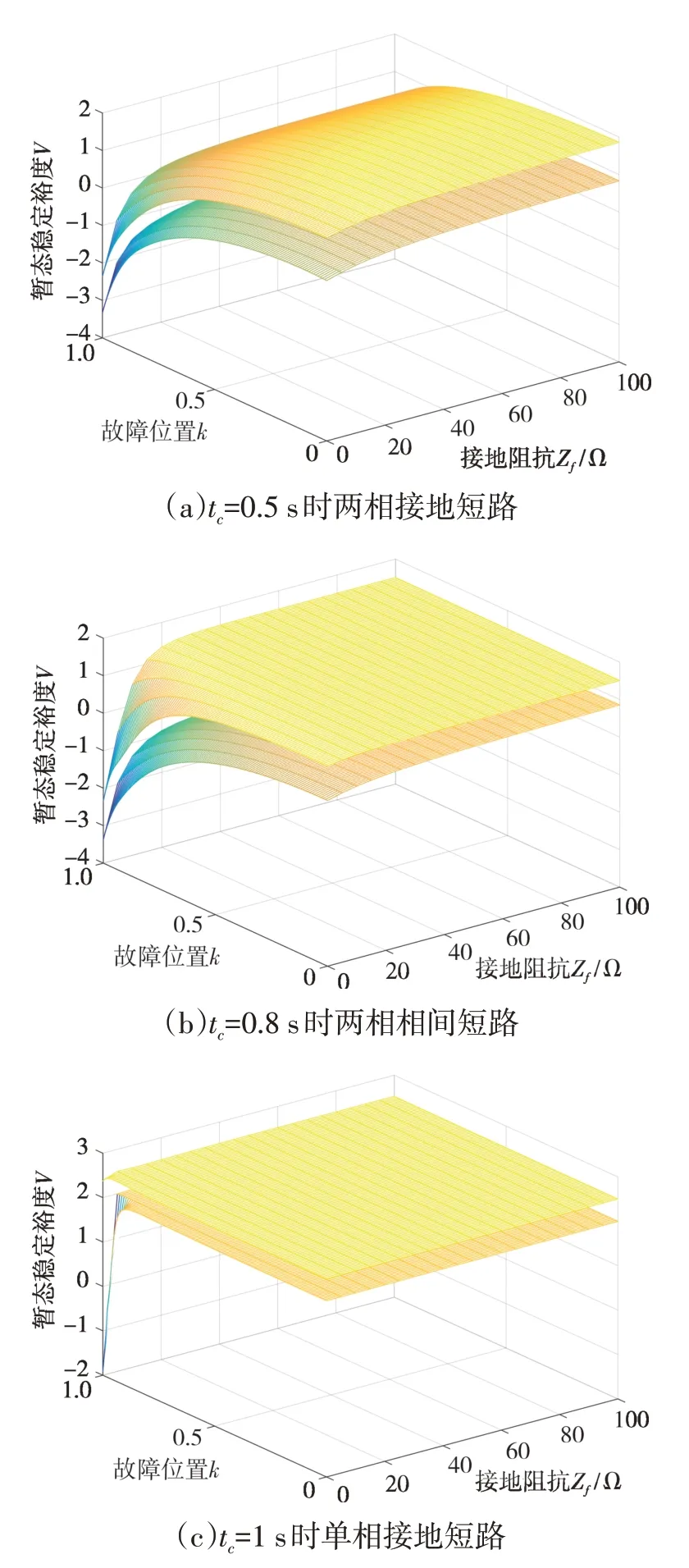
图10 不同故障类型下V与k和Zf关系曲面Fig.10 Relationship surface of V varying with k and Zf under different faults

提取图10中暂态稳定裕度曲面与平面V=0的交线，即可得到不同故障类型下原始系统与含双馈风电场系统的暂态稳定边界，如图11所示，其中蓝线和红线分别为原始系统和含双馈风电场系统的稳定边界，边界左侧和右侧分别是系统的稳定区域和失稳区域。可以看到，接入双馈风电场后三种不对称短路类型下（k，Zf）坐标平面上的失稳区域均有不同程度增大，在两相接地短路下尤为明显。值得注意的是在单相接地短路下，故障持续时间为1 s时对于任意（k，Zf）组合原始系统均不会失稳，而加入风电场后坐标点（1，0）附近区域开始出现失稳。

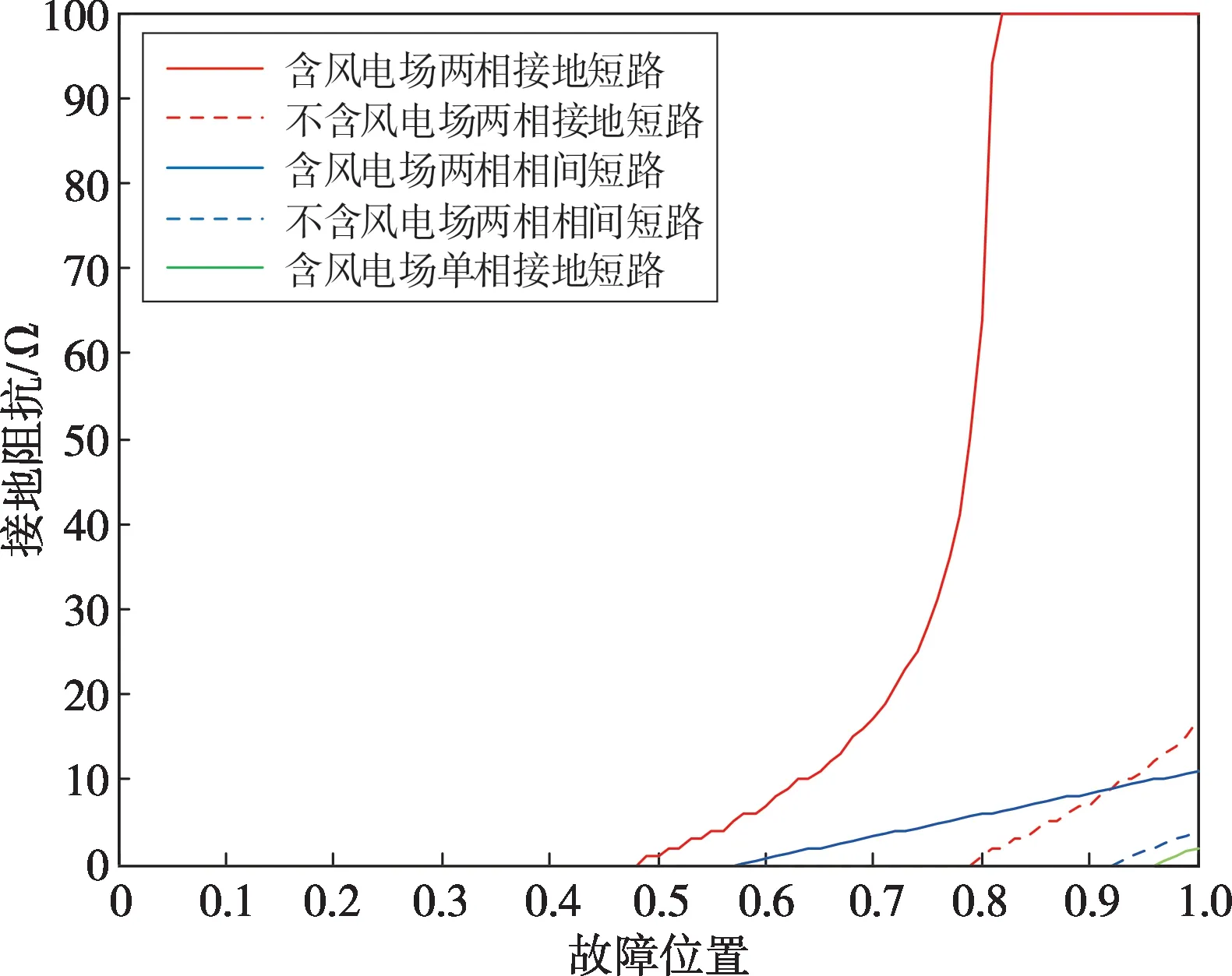
图11 不同故障类型下系统暂态稳定边界Fig.11 Transient stability boundary of the system under different fault types

为分析风电场负序阻抗对系统暂态稳定裕度影响，对不计风电场负序阻抗下系统稳定裕度V'进行了计算并与本文方法得到的稳定裕度V进行对比，令ΔV=V'-V，得到ΔV二维曲面如图12所示，可以看到除两相故障下的小部分区域外，ΔV取值均大于0，说明在大多数情况下忽略风电场负序阻抗的影响会造成系统暂态稳定性增大，使得判断结果过于乐观，甚至导致某些失稳的（k，Zf）区域被误判为稳定，从而给系统稳定性带来隐患。

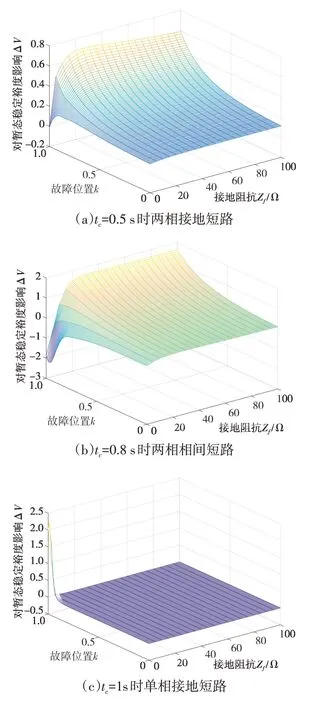
图12 不同故障类型下ΔV与k和Zf关系曲面Fig.12 Relationship surface of ΔV varying with k and Zf under different faults

4 结论

本文根据双馈风电场在故障期间以及故障切除后的等效外特性，将包含风电场等效导纳、风电场负序阻抗、故障发生位置以及故障接地阻抗在内的故障信息引入暂态稳定性判断中，通过对含双馈风电场的3机9节点系统进行仿真验证，得出以下结论：

1）不对称故障下，双馈风电场负序阻抗的幅值和相角均随故障类型和故障发生位置的变化而改变。

2）加入双馈风电场后系统的暂态稳定裕度曲面及暂态稳定边界较不含风电场时将发生变化，且不同故障类型下其变化程度不同。如忽略风电场负序阻抗的影响，通常会造成系统暂态稳定性增大，使得判断结果过于乐观。

3）针对同一故障类型，系统暂态稳定裕度受故障发生位置、接地阻抗以及风电场负序阻抗等因素共同影响，忽略上述因素会导致系统暂态稳定判断结果出现误差，甚至可能会发生误判。

本文以双馈风机为研究对象，对故障期间风机的负序阻抗变化情况及对系统暂态稳定裕度的影响进行了探究，下阶段将进一步对直驱风机等其他类型风机开展研究。