影响圆柱度检测精度的因素探究

柯昌全，张 蕊，岳文兵，徐文祥

影响圆柱度检测精度的因素探究

柯昌全，张 蕊，岳文兵，徐文祥

（陕西法士特齿轮有限责任公司，陕西 西安 710117）

在机械加工过程中，为进一步提高圆柱度检验精度，标准化规范化检验，通过对影响圆柱度检测精度的因素进行研究，得出高斯滤波范围选取对测量结果的影响，针对不同圆柱直径选取适合的高斯滤波范围；同时对测量选取截面数以及轴向有效测量长度进行探究，得出了合理的选取数量及轴向有效测量长度。通过对上述影响圆柱度检测精度的因素进行优化，提供一套规范合理的检验方法，提升生产过程中圆柱度检测精度，保障检测结果的可靠性，对产品的质量控制具有重要意义。

内孔圆柱度；高斯滤波；圆柱度检测；截面数；有效检测长度

随着科学技术的不断进步，各行业对机械产品加工精度的要求越来越高，检测技术作为机械制造业的重要组成部分，在其中发挥着重要作用。在制造水平不断提升的同时，测量技术的改进提升也势在必行。

汽车零部件涉及各零部件之间的装配配合，由于人们对汽车零部件的精度要求越来越高，汽车零部件行业逐渐标准化、规范化。当下，市场对于汽车零部件精度的要求大幅提升，加工手段也在不断革新，对应的检测规范若仍然沿用以前的惯例，高精度的检测要求势必造成检测结果与真实值有较大偏差，无法满足客户需求，故研究影响检测各类特征精度的因素对于提升产品质量有重要意义。

1 影响圆柱度检测精度的主要因素

圆柱度误差是指实际被测圆柱面对其理想圆柱面的变动量。圆柱度误差的测量大多采用坐标测量法，多使用圆柱度仪和三坐标测量机等。圆柱度公差最能体现对圆上因素的横截层面、轴横截面轮廊线和中轴线的样式误差值综合性操控规定，因此，它能最直接反映出零部件的相互配合精密度和性能指标规定。汽车零部件生产制造中零部件圆上因素诸多，且多见关键的相互配合位置，其精密度直接反应着设备的性能指标。

影响圆柱度检测精度的因素很多，包括检测设备差异、检测人员差异、检测环境、评定方法等，除这些固定因素外，从技术层面，影响圆柱度检测精度的因素主要包括高斯滤波范围、选取截面数和轴向有效取样长度三个方面。本文就以上三个因素对圆柱度检测精度可能造成的影响进行分析研究。

1.1 高斯滤波范围

1.1.1高斯滤波的本质

在评价圆柱度的过程中，为了减少或者消除不必要的因素影响，对所获得的轮廓通常要进行滤波处理。

高斯滤波是一种信号平滑处理的技术方法，是一种线性滤波，坐标测量技术中的标准滤波算法，使用高斯曲线加权计算测量点得到新的轮廓使用的范围比较广泛，一般用于封闭元素，其对信号的处理过程实质上是一种对数据加权平均的过程，即处理后每一个点位上的数据，是由其本身和领域内其他点位的数据加权平均后得出，理论简易模型如图1所示[1]。

由图1可见，中心点位的原始数据为2，经过高斯滤波（模式加权系数为1）后，变为图2。实际应用中的高斯滤波远比图示复杂，但基本原理是一样的。

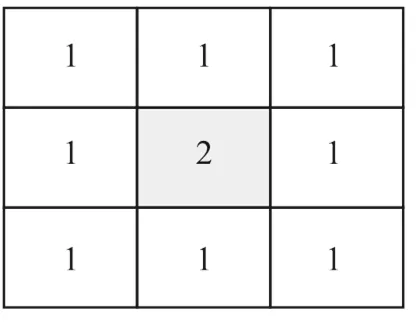
图1 原始数据

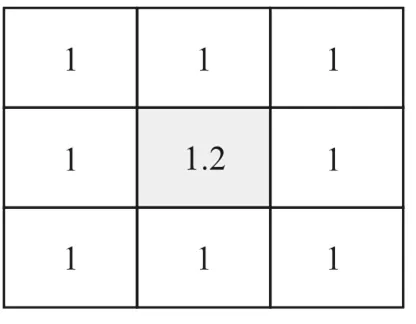
图2 高斯滤波后

1.1.2高斯滤波在圆柱度检测中的应用

探针在工件表面扫描时能够提取到很多表面信息，如表面现状、波纹度、部分粗糙度等，这些特征是叠加的，通过滤波将从工件表面测量出来的数据，分解成多个单独的数据波。滤除波纹度和粗糙度对形状偏差的测量影响是本文进行滤波的重要意义。

高斯滤波主要是通过影响各检测截面上的圆度来间接影响圆柱度的。要用高斯滤波分析一个截面的圆度，首先要消除圆度检测中的边界效应。

所谓边界效应，是指在测量要素的边界位置上，因为各种因素的影响，测量误差会比其他区域大。

高斯滤波中，为了消除边界效应，采用切补的方式，对边界进行处理。将整个测量长度看成一个首尾相接的圆，然后在整圆的基础上，掐头去尾，再将去除的部分用其他部分补回来。

以圆周的测量为例，如图3所示。假如该圆周采用逆时针采样，将采样区域分为等份，其中，起始区域标记为区域1；终止区域标记为区域2；紧邻起始区域和终止区域的两个区域分别标记为区域3和区域4。对边界进行处理时，先将区域1和区域2移除，再将相邻的区域3和区域4各自复制，补到原来区域1和区域2的位置，重新形成一个整圆。

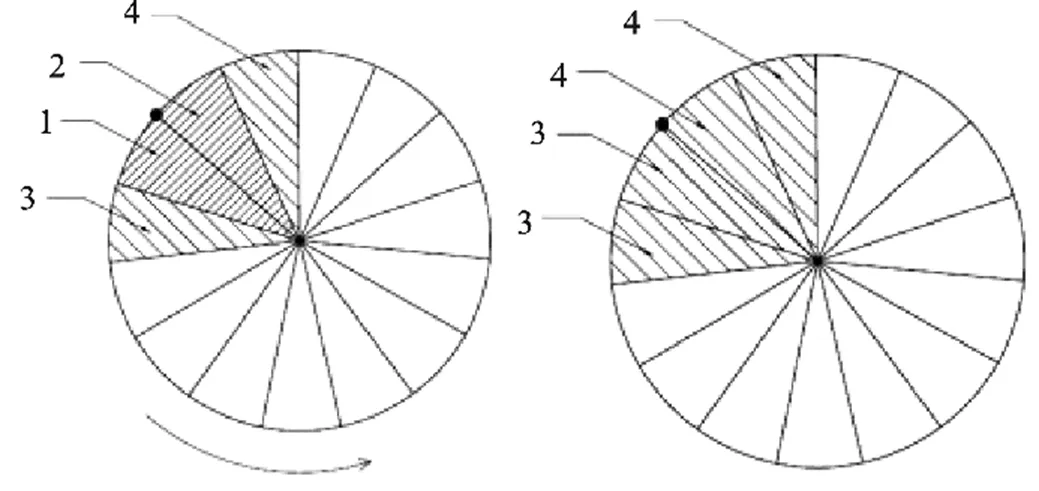
图3 切补法消除边界效应

通过图3可以看出，圆周被等分的份数越多，起始区域和终止区域所占的比例越少，分析时整个圆周的还原度越高，测量结果越趋近于真实值，即测量结果越精确。但是，过分追求等分份数的增多，会导致起始区域和终止区域的过分减少，从而失去消除边界效应的意义。

1.1.3高斯滤波范围的选取

上述等分的份数在高斯滤波中是非常重要的一个参数，因为这里的等分份数也将是最终圆度分析图形上呈现的波动数。简单来说，如果取15，那么高斯滤波后整个图形将有15个波动点；如果取50，那么高斯滤波后整个图形上将有50个波动点。各个波动点的形成用的就是文章开头的加权平均法。

等分份数的学名为截止波数，在实际检测中作为滤波范围的指标，单位为upr。upr是undulation per revolution 的简写，即每个圆周上的波动数。滤波的过程就是将从工件表面测量出来的数据，分解成很多个单独的数据波，每个单独的波就是一个upr[2-6]。

通过图4、图5可以直观看到，对于同一内孔同一个圆周，等分成50份（=50 upr）进行高斯滤波后，各分区内加权平均后的图形比较圆润，形状更规则；等分成150份（=150 upr）进行高斯滤波后，各分区内加权平均后的图形比较尖锐，形状比较杂乱。对应的，两者检测出来的圆度值也有明显差异，前者为0.007 3 mm，后者为0.011 8 mm。

理论上分析，在检测总点数相同的情况下，截止波数的大小，直接决定了每个区域内点数的大小。的数值大，表示同一区域内的点数多，加权平均之后数值趋近理论圆，形状平缓，圆度数值小；的数值小，表示同一区域内的点数少，加权平均之后偏离理论圆，形状尖锐，圆度数值大。

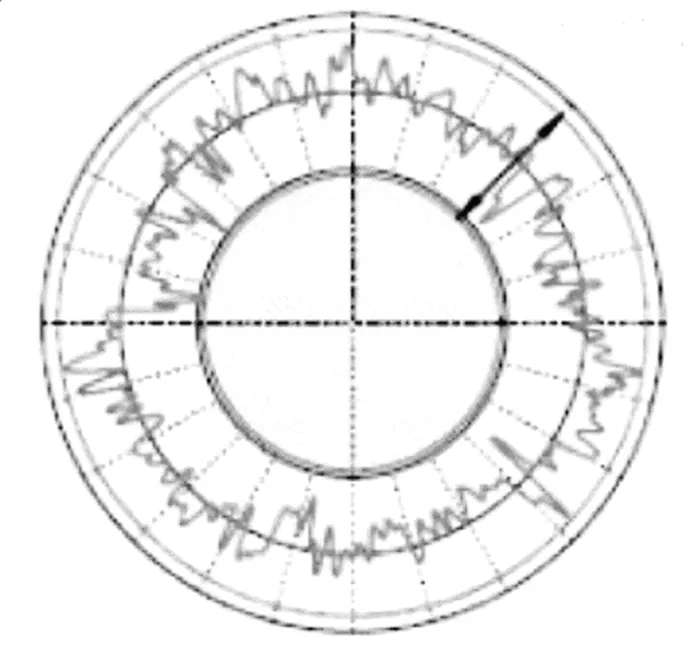
图5 150 upr滤波轮廓

但是，盲目追求截止波数的增大，会造成每个区域内测量点数的急剧减少，加权平均后与原来各点位基本一致，也就失去了高斯滤波的意义，因此，高斯滤波范围的选取应该在一个合适的范围内。

针对该问题，国际产品几何量技术规范《产品几何技术规范（GPS）圆柱度第2部分：规范操作集》（ISO/TS 12180-2:2003）给出了建议取值范围，可以作为圆柱度检测规范中的参考，如表1所示。针对不同直径的零件，一直选用=50 upr的滤波范围，显然是不科学的，参照国际方法后在圆度和圆柱度的检测精度上会有提升。

表1 高斯滤波取值范围

圆柱直径/mm滤波范围/upr D≤88＜D≤251～151～50 25＜D≤8080＜D≤250250＜D1～1501～5001～1 500

1.2 选取截面数

截面数是指在圆柱度检测时，选取的截面数量。针对同一个圆柱，选取的截面数不同，测量出的圆柱度值也会有一定差异。关于截面数的选取，目前国际和国内均无相关标准。

理论上，两个截面即能定义一个圆柱，但两个截面之间的真实情况无法被反映。笔者公司长期选用三个截面，国外的一些齿轮公司则建议选用四个截面。为此，本文针对同一个内圆柱面（直径46.6 mm，长度35 mm），进行了三个截面和四个截面的多次检测对比分析，发现两者的圆柱度差值在0.000 8 mm左右。而且通过图6三截面检测轮廓和图7四截面检测轮廓对比，显然四个截面更能反映圆柱的真实情况。

图6 三截面检测轮廓

图7 四截面检测轮廓

考虑到笔者公司零件圆柱面的涵盖范围很广，始终选用固定的截面数无法反映柱面的真实情况，本文参考卡特彼勒公司对于花键锥度的测量方案，对不同长度圆柱面的选取截面数区别对待。同时，考虑到不同精度要求的圆柱面，其选取的截面数也应该不同。综合这两方面的因素，针对不同长度和不同公差要求的圆柱度检测截面数做如表2所示的规定，方便现场执行。

表2 检测截面数k 单位：个

长度/mmλ≤0.008 mm0.008 mm＜λ≤0.02 mmλ＞0.02 mm L≤50L＞50343333 L＞75L＞100L＞125L＞150567744453445

检测截面数的取值遵循以下几个基本原则：

1）考虑到检测结果的可靠性，的取值不能小于3；考虑到实际检测过程中的工作强度和工作效率，的取值不大于7。

2）各检测截面在圆柱面的轴线方向应该均匀分布。当圆柱面的轴向长度超过50 mm时，相邻检测截面之间的距离维持在25 mm是理想选择。

3）各检测截面上的检测状态应该保持一致。

1.3 轴向有效检测长度

轴向有效检测长度是一个容易被忽略的要素，尤其是在一些细长的柱面中，检测长度直接影响最终的圆柱度检测结果。以实际检测为例：一个直径83 mm、长度80 mm的内孔，当有效检测长度为30 mm时，圆柱度值为0.003 7 mm；有效检测长度延伸值为64 mm时，圆柱度值为0.005 4 mm。

在实际检测中，因为零件结构、测头大小等因素的影响，很难检测整个圆柱面，但为了保证检测结果的精确性，经过现场论证，有效检测长度应该至少达到整个柱面长度的80%以上。

2 总结

通过多方论证和研究，高斯滤波范围、选取的截面数和轴向有效检测长度是影响圆柱度检测结果非常重要的三个方面。本文对以上三个因素做了梳理总结，整理出了满足现场和客户需求的圆柱度检测要素规范，即针对不同的零件直径选取合适的滤波范围；检测截面数不小于3不大于7时，截面在轴线方向应当均匀分布，各截面检测状态应当保持一致；有效检测长度应该至少达到整个柱面长度的80%以上。本研究对圆柱度检测精度的提升有重要作用。

[1] 许景波,袁怡宝,刘泊,等.圆度测量中高斯滤波的逼近实现办法[J].计量学报,2012,33(1):16-20.

[2] 许景波,袁怡宝.圆度测量中的高斯滤波快速算法[J].南京理工大学学报(自然科学版),2007(3):342-345.

[3] 高作昆,赵则祥,席建普,等.数字滤波在圆柱体要素提取中的应用[J].传感技术学报,2007(7):1568-1572.

[4] 温文炯,温英明.基于三坐标提取点数据的圆柱度误差的评定方法[J].机械工业标准化与质量,2021(7): 29-33.

[5] 史栩屹,李明,韦庆钥.二次插值鲸鱼优化算法在圆柱度误差评定中的应用[J].计量与测试技术,2019,46(2): 58-60.

[6] 周鑫,张琳娜,赵凤霞,等.基于GPS的圆柱度公差建模及其规范设计研究[J].机械设计与制造,2012(4): 29-31.

Research on the Factors Affecting the Accuracy of Cylindricity Measurement

KE Changquan, ZHANG Rui, YUE Wenbing, XU Wenxiang

( Shaanxi Fast Gear Company Limited, Xi'an 710117, China )

In the process of machining, in order to further improve the accuracy of cylindricity measurement and standardize the measurement, the factors affecting the accuracy of cylindricity measurement are studied,and the influence of the selection of Gaussian filter range on the measurement results is obtained. Suitable Gaussian filter range is selected for different cylindrical diameters. The tangent and complement method is used to eliminate the boundary effect in the process of Gaussian filtering. At the same time, the selected section number and axial effective measurement length are explored, and a reasonable selection number and axial effective measurement length are obtained. By optimizing the above factors affecting the cylindricity measurement accuracy, a set of standardized and reasonable inspection methods are provided to improve the cylindricity measurement accuracy in the production process and ensure the reliability of test results, which is of great significance to the quality control of products.

Inner hole cylindricity; Gaussian filter;Cylindricity measurement;Number of sections;Effective measuring length

TG835

A

1671-7988(2023)18-136-04

柯昌全（1989－），男，工程师，研究方向为齿轮加工工艺和智能制造，E-mail:00002805@fastgroup.cn。

国家科技重大专项资助项目（2015ZX04003006）。

10.16638/j.cnki.1671-7988.2023.018.026