基于Kullback-Leibler散度的多指标群体评价算法研究

杨 波, 方 杰

1.乐山市科学技术情报研究所,四川 乐山 614000 2.四川省计算机研究院,四川 成都 610041

0 引言

目前,科研管理中对科研人员的业绩和水平考核采用量化打分模式,存在着一定的主观性,导致诸多科研业绩评价和考核结果均存在重数量、轻质量的现象。随着科研改革的深入,许多高校引入了同行评议机制,邀请业内多位专家进行评价,但如何对评价指标和权重进行设置和调整成为实践中遇到的难题。

从数学模型看,此类问题属于多目标、多人、多因素评价问题(以下简称多指标群体评价),在计算机领域属于非确性多项式(nondeteministic polynominal,NP)问题,求解困难[1]。多目标多人多指标评价问题是当前处理社会经济系统规划与管理问题的最为有效的工具,在管理、经济、军事等领域有着广泛的应用,成为当今评价科学的热门研究方向[2]。

多指标群体评价着重研究评价指标中的权重问题,但当前学术界的研究成果均存在一定的局限性[3]。概括起来,可分为以下几类:客观赋权法中需要使用复杂数学模型求解,计算量大,且缺乏能代表专家偏好的决策因素;主观赋权法中受决策者的经验影响,决策结果具有较强的主观随意性;主客观赋权法需要将决策者的主观偏好和客观属性信息进行结合,但由于主观偏好和客观属性的量纲不一致,集成处理难度大,较难用于工程实践[4]。

本文首先分析了现有多指标群体评价研究中存在的问题,然后利用信息熵原理,求解出评价指标的客观权重。最后,基于Kullback-Leibler散度反映不同指标权重之间的距离,建立优化模型,求解出群体决策条件下指标的集成权重,为多指标群体评价问题提供新的解决思路。

1 现有评价算法及存在的问题

现有的多指标群体评价问题将建立评价对象、评价指标、评价者(专家)、指标权重之间的数学关系用集合和矩阵等进行描述。

一般地,设S={s1,s2,…,sn}为多指标群体评价问题的评价对象集合(科研工作者提供的科研业绩),F={f1,f2,…,fm}为工作业绩评价的指标集,权重向量W={ω1,ω2,…,ωm},专家对科研工作者的业绩si关于指标fj的评价值为xij,i∈N,j∈M,其中,N={1,2,…,n},M={1,2,…,m}。

首先,经标准化处理后X=(xij)n×m变成Z=(zij)n×m,然后,假定集成后的权重可表示为:

W={ω1,ω2,…,ωm}T

(1)

针对式(1)的求解,文献[5]给出了一种基于属性权重优化的多属性群评价专家权重调整算法,构造了等权的线性加权法单目标最优化模型:

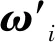
文献[6]考虑了评价矩阵的客观信息和评价者的主观偏好,提出了离差函数定义:

式中:ωj为集成后的权重,ukj为主观赋权法对指标确定的权重,类似可以定义客观权重与集成权重之间的离差函数。

依此可构造目标规划模型,使得总的离差最小,即:

式中:αk为主观赋权法和客观赋权法的权系数,μ为调节因子,调节主观权重和客观权重的占比。此规划模型存在的问题主要是求解较为复杂,且需要根据专家经验反复调整参数,实用性不强。

综上可知,现有的多指标群体评价算法需要人为调整参数,具有主观性,且计算过程较为复杂,计算机程序实现较为困难。

2 基于Kullback-Leibler散度的多指标群体评价算法

2.1 符号说明及相关定义

将科研业绩评价问题描述成为一个四元组:(A,C,D,X)。其中,A={ai|i=1,2,…,m}为科研工作者的业绩集合;C={cj|j=1,2,…,n}为评价指标集;D={dk|k=1,2,…,s}为同行评议专家集,k大于等于2;第i个科研业绩的第j个指标的评分值为xij。

通过组织同行专家对科研工作者的科研业绩进行打分,可构建专家评价矩阵X,即:

多指标群体评价是指专家数不能少于2个,群体评价模型中需要考虑专家之间的差异以及对群体决策意见的影响程度。在群体决策条件下,指标的权重会发生变化,需要通过数学模型去刻画这种变化。

利用加权和公式即可计算出第k个专家对科研工作业绩i的打分:

式中:βj为指标cj的主观权重,且满足0≤βj≤1,j=1,2,…,n。假定群评价专家的集成权重为ωj,j=1,2,…,n,则专家群评价条件下,第i个业绩的评分为:

(2)

在群体评价中,专家的集成权重与评价指标的客观权重和专家之间的差异均有关系。因此,如何利用已知的决策信息求解集成权重为ωj尤为重要。

2.2 基于熵权法确定评价指标的客观权重

根据信息熵的原理,第j个指标出现的概率为:

经过近几年产业结构调整，公司内部治理的完善，公司产品早已走出国门，向缅甸、越南、马来西亚、印度、沙特阿拉伯、保加利亚、德国、俄罗斯等国家出口。2018年6月份，子公司云天化联合商务再创佳绩，7.25万吨磷酸二铵的巴拿马型化肥船在辽宁营口港成功出运，再次刷新今年5月中旬由联合商务创造的6.9万吨中国磷肥行业最大单船出口量纪录。

若某个指标的信息熵越小,表明在专家决策中所起作用越大。因此,第j个指标的熵为:

定义信息效用值θ=1-Ej,熵越小,信息效用值越大,已有信息量越多。将信息效用值进行归一化处理,就可以得到每个指标的熵权,即可视为评价指标的客观权重,令其为μj,可知:

(3)

2.3 基于Kullback-Leibler散度确定群体评价的集成权重

Kullback-Leibler散度(KL散度)来源于概率论和信息论中的概念。KL散度的定义是建立在熵(Entropy)的基础上的,在统计学意义上来说,KL散度可以用来衡量2个分布之间的差异程度。若两者差异越小,KL散度越小。

假定p(x)=(p1,p2,…,pn)和q(x)=(q1,q2,…,qn)为同一随机事件X的2个概率分布,p(x)分布的信息熵为:

q(x)分布的信息熵为:

则KL散度为:

KL散度越小,表示p(x)和q(x)2个概率分布更加接近。

假定群评价集成权重为ωj=(ω1,ω2,…,ωn),利用KL散度准则,建立如下优化模型。

式中:(λ-1)为拉格朗日乘子,分别对ωj和λ求偏导,得到如下方程组。

最终求解得到集成权重:

(4)

2.4 算法流程

步骤1:引入专家同行评议机制,根据评价指标,专家对科研业绩进行打分;构建科研业绩评价专家评分矩阵X,对评价指标集进行规范化处理。

步骤2:采用式(3),基于熵权法计算各评价指标的客观权重μj。

步骤3:利用KL散度准则,建立优化模型,求解出集成权重ωj,将集成权重ωj代入式(2),得到对科研业绩的评价值。

3 算例分析

某学院邀请业内5位专家对4位科研工作者的业绩从科研项目和平台、科研成果与奖励2个方面进行综合评价,构建的评价指标体系如表1所示。

表1 科研业绩评价指标体系

5位专家对4位科研工作者业绩评分后,参照算法流程中的步骤1,对指标做一致性处理并消除量纲,得到处理后的评分矩阵X;参照算法流程中步骤2,基于熵权法计算评价指标的客观权重;参照算法流程中的步骤3,利用KL散度准则,建立优化模型,求解出集成权重,如表2所示。

表2 权重表

由表2可知,客观权重的计算结果表明,现有的指标体系较重视奖励数量(A8)和奖励级别(A7);在专家群体评价中,集成权重的计算值表明专家更看重成果的水平(A5)和奖励的级别(A7),这个是引入同行评议机制带来的转变,更加看重学术成果的水平和奖励的质量,而不是盲目看重科研成果的数量。

将表2中获取的集成权重,代入式(2),可计算出科研工作者的业绩排序为:

X4>X2>X1>X3

本文提出的算法与文献[7]和文献[8]在计算时间上进行比较,结果如下。

表3 算法效率比较

由表3可知,本文提出的算法在计算时间上比另外2种算法快。究其原因,是因为本文提出的算法通过KL散度准则确定集成权重时,能从概率上逼近评价指标的先验分布概率,无需反复迭代和人为调整参数。

4 结束语

本文研究多指标群体评价问题,针对主客观赋权法存在数学模型复杂、计算量大和反复调整等问题,提出了一种基于信息熵理论的权重集成方法,通过引入同行评价机制,可较好地应用于科研业绩评价。

在日常实践中,对科研工作者的科研业绩进行考核时使用的评价体系不一致,评价指标较为繁杂,指标集规范化处理难度较大。在应用本文模型和算法时,除了引入同行评价机制,还需要根据实际对指标体系进行优化,使其更加符合科研业绩评价的实际需求。