改进滑模控制双降压式逆变器的动力学特性
陶 慧,艾朋伟
(河南理工大学电气工程与自动化学院,焦作 454000)
电力电子变换器是一种强非线性时变系统,存在着倍周期分岔、Hopf 分岔及混沌等非线性行为[1-2],这些非线性行为会影响系统的稳定运行。近年来,DC-AC逆变器的非线性研究受到广大学者的关注。文献[3]首次研究了比例控制的H 桥逆变器的分岔和混沌现象。文献[4]研究了H 桥逆变器在比例积分控制下的非线性行为,采用快变稳定性定理进行了理论分析,给出了各电路参数的稳定工作范围。文献[5]研究了准比例谐振PR(proportional resonant)调节下一阶H 桥逆变器的非线性现象,建立了系统一阶离散数学模型,并运用雅可比矩阵进行了理论分析。文献[6]在文献[5]的基础上研究了三相并网逆变器的非线性现象,建立了三相逆变器的离散数学模型。但上述研究都是对线性控制下H桥逆变器的非线性行为进行分析。
滑模控制是一种典型的非线性控制方式,具有响应速度快、鲁棒性好、自适应性强等优点,其与改进指数趋近律结合还能够有效消弱抖振[7]。因此,改进指数趋近律滑模控制在逆变器控制中有广阔的应用前景。文献[8]结合分岔图和折叠图,研究了改进指数趋近律滑模控制下的H桥逆变器,发现其具有非常丰富的动力学行为。
上述线性控制与非线性控制逆变器研究都以传统的H 桥逆变器为研究对象。而随着电力电子技术的发展,对逆变器性能的要求也越来越高。传统的H 桥逆变器结构简单、应用广泛,但存在桥臂直通问题,在实际工程中,需要设置死区时间,但如果死区时间设置不当,会引起输出电压的严重畸变。为此,吴婷等[9]提出一种对称电感配置的双降压式逆变器,该电路结构在同一桥臂的两开关管之间放置滤波电感,解决了桥臂直通问题。双降压式逆变器具有无需设置死区时间、可靠性高、电能质量高和直流电压利用率高等优点,因此广泛应用于对电能质量和可靠性要求较高,以及高电压和高功率输出的场合。文献[10]研究了比例控制下双降压式逆变器的非线性行为,通过分岔图和折叠图分析了比例系数对系统稳定性的影响,但没有进行稳定性理论分析。
本文将改进指数趋近律滑模控制引入到双降压式逆变器中,并对其动力学特性进行研究。首先分析系统工作原理,利用频闪映射法建立系统的离散模型,然后结合数值仿真方法研究控制参数和外部参数对系统稳定性的影响,最后利用快变稳定性定理进行理论分析。本文研究将为双降压式逆变器的控制提供新思路,为改进指数趋近律滑模控制方式下逆变器的设计和调试提供一定的理论依据。
1 逆变器的工作原理及离散模型
1.1 工作原理
采用改进指数趋近律滑模控制具有抖振小、响应快、鲁棒性强等优点。改进指数趋近律滑模控制双降压式逆变器的电路原理如图1 所示。该逆变器由主电路和控制电路两部分组成:在主电路中,E为直流电压,VT1~VT4为4 个全控型开关,D1~D4为4 个续流二极管,逆变侧的滤波器由电感L1~L4和电容C组成,R为负载;在控制电路中,首先将参考电流iref=Imsin(ωt)与电感电流iL比较得到误差信号e,即e=iref-iL,然后将误差e输入至改进指数趋近律滑模控制器得到控制电压ucon,最后将控制电压ucon作为调制波与双极性三角波utri进行调制得到驱动VT1~VT4的脉宽调制PWM(pulse width modulation)信号,根据半周期工作方式驱动各开关管。
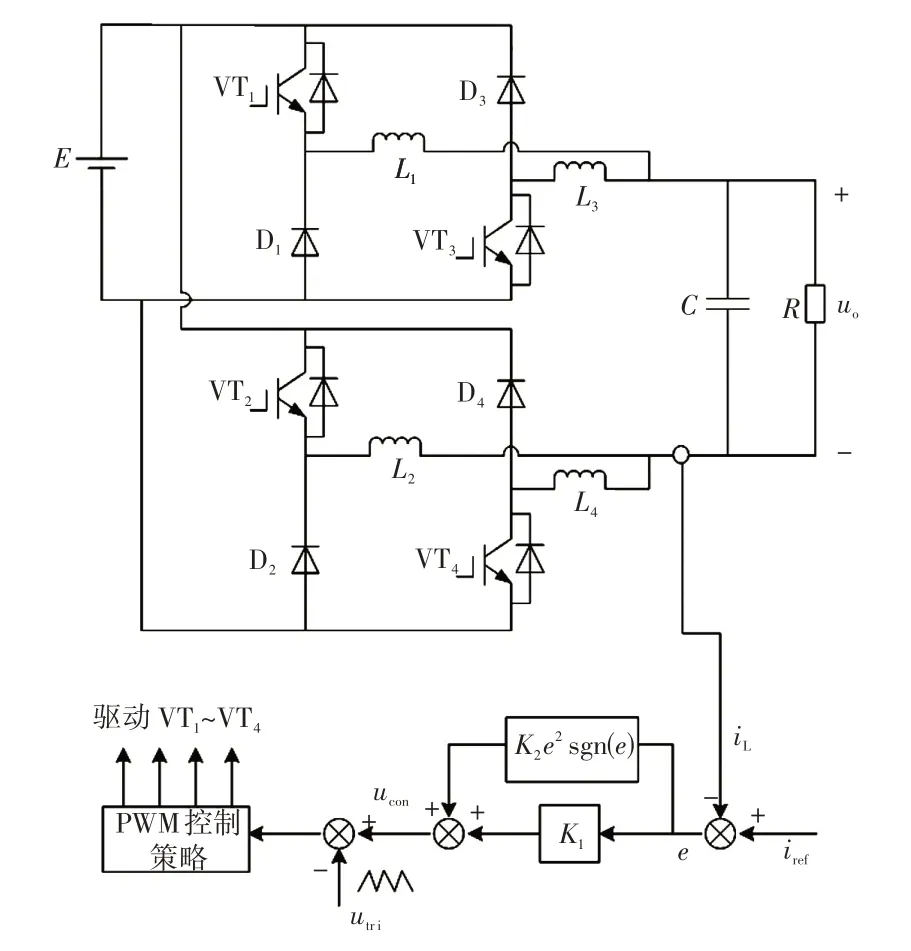
图1 改进指数趋近律滑模控制双降压式逆变器的电路原理Fig.1 Circuit principle of a double buck inverter with improved exponential approach law sliding mode control
采用半周期工作方式的PWM 控制策略如图2所示[10]。控制电压ucon与0 V 相比较可得到实现半周期工作的方波信号,将方波信号与PWM 信号相与可得到开关管VT1、VT4的驱动信号SVT1,VT4;然后将方波的反相信号与PWM的反相信号相与得到开关管VT2、VT3的驱动信号SVT2,VT3。此运行模式可以减小器件的开关损耗和导通损耗。

图2 PWM 控制策略Fig.2 PWM control strategy
为了方便分析,假设所有开关管、二极管及电感电容均为理想器件,且取L1=L2=L3=L4=L;S表示开关管的状态,当S=1时开关管导通,当S=0时开关管截止。根据iL的正负及开关管、二极管的状态,系统可分为以下4种工作状态。
(1)当iL>0 时,若ucon>utri,则S= 1,开关管VT1、VT4导通,VT2、VT3截止;若ucon 式中:iL为电感电流;uo为输出电压。 (2)当iL<0 时,若ucon 采用改进指数趋近律滑模控制,控制电压ucon可表示为[7] 式中:K1为比例系数,K1>0;K2为滑模控制系数,K2>0。 PWM控制下的占空比d为 式(3)和式(4)组成了控制电路的状态方程。 采用频闪映射方法进行建模,以开关周期T作为频闪采样的时间间隔。令Xn=[iL,n,uo,n]T,Xn为第nT时刻的状态变量矩阵,状态变量iL,n为第nT时刻的电感电流,uo,n为第nT时刻的输出电压。 由式(1)和式(2)可得 其中 式中:Ai为状态矩阵,i=1,2,3,4;Bi为输入矩阵;X为系统状态变量矩阵,X=[iL,uo]T。 主电路的离散数学模型为 式中,I为二阶单位矩阵。 对式(3)离散化可得第n个开关周期的控制电压为 式中,iref,n为第n个开关周期的参考电流。 根据准静态思想可得 由式(4)和式(10)可得第n个开关周期的占空比dn为 由于占空比具有饱和特性,需对dn进行限幅处理,即 整个系统的离散模型由式(6)~(13)组成。 常用的非线性动力学数值研究方法有分岔图、折叠图、时域波形和频谱图。分岔图通过对不同周期下状态变量输出波形的同一位置进行采样得到,可以反映出分岔临界点并分辨出系统出现的分岔类型。折叠图通过对稳定后的多个正弦周期进行采样并将采样点一一叠加得到,可以直观地反映系统整个输出周期的稳定状态。当折叠图是1 条正弦曲线时,系统稳定运行;当折叠图是2 条以上曲线或不规则的点分布整个区域时,系统工作在不稳定状态。时域波形通过在Matlab/Simulink 中搭建电路仿真得到,可以定量描述系统振荡周期与时钟周期的关系,进而判断系统的稳定性。频谱图通过对状态变量的时域波形进行快速傅里叶变换FFT(fast Fourier transform)分析得到,能够观察到对应时域波形中所含的谐波成分及总谐波失真THD(total harmonic distortion),进而判断系统稳定性与电能质量优劣。 本文分别采用分岔图、折叠图、时域波形及其频谱图等研究控制参数对系统稳定性的影响。电路参数分别设置为E=180 V,R=10 Ω,L=5 mH,C=50 μF,fs=5 kHz,f=50 Hz,iref=12 sin(100πt)。 令K2=0.1,其他电路参数保持不变,K1以0.003 的步长从0 变化到1,在电感电流波形峰值和谷值处分别采样,绘制出以K1为参数的分岔图如图3所示。将图3与文献[8]中相关分岔图4对比发现,本文系统没有出现H桥逆变器的多种倍周期同时存在的特殊分岔现象;状态变量在峰值处与谷值处采样的分岔特性相同,系统的非线性复杂度大大降低,这是因为系统的半周期工作方式减少了半个周期内开关管的开关个数,以及对称电感配置的双降压式逆变器具有较H 桥逆变器更加对称的电路结构。 图3 以K1 为参数在峰值与谷值处采样的分岔图Fig.3 Bifurcation diagrams sampling at peak and valley with K1 as parameter 图4 K1 分别取0.20、0.43、0.80 时的折叠图Fig.4 Folding diagrams when K1 takes 0.20,0.43 and 0.80 respectively 从图3 可看出,当0 K1分别取0.20、0.43、0.80 时的折叠图如图4 所示。图4(a)中呈现1条正弦曲线,且K1=0.20处于分岔图(见图3)的0~0.35 区间,说明此时系统处于稳定运行状态;图4(b)中呈现2 条正弦曲线,且K1=0.43 处于分岔图(见图3)的0.35~0.45 区间,说明此时系统处于周期2状态;图4(c)呈现出大量复杂无规律的点填充了大部分区域,且K1=0.80处于分岔图(见图3)的0.45~1.00区间,说明此时系统处于混沌状态。可见,折叠图(见图4)与分岔图(见图3)的分析结果一致,验证了系统离散模型和数值仿真的正确性。 K1分别取0.20、0.43、0.80 时的时域波形(含峰值附近局部放大图)和频谱图如图5~图7所示。在频谱图中,横坐标f表示频率,纵坐标Mag表示各频率下的谐波相对基波的百分比。由图5(a)可知,iL为正弦波形,振荡周期等于时钟周期;由图5(b)可知,iL中主要存在基波分量和开关频率及其附近谐波分量,此时THD 较小为6.36%,系统处于稳定运行状态。图6(a)中iL的振荡周期是时钟周期的2倍;图6(b)中iL主要存在基波分量、开关频率和0.5开关频率及其附近谐波分量,此时THD 为8.27%,系统处于倍周期状态。图7为K1=0.80 时的时域波形和频谱图。图7(a)中iL的时域波形失去周期性,变得混沌;图7(b)中存在大量多种非基波频率与开关频率的谐波分量,此时iL的THD较大为11.63%,系统处于混沌不稳定状态。可见,时域波形及频谱图的分析结果与折叠图及分岔图的分析结果一致。 图5 K1=0.20 时的时域波形和频谱图Fig.5 Time-domain waveform and frequency spectrum at K1=0.20 图6 K1=0.43 时的时域波形和频谱图Fig.6 Time-domain waveform and frequency spectrum at K1=0.43 图7 K1=0.80 时的时域波形和频谱图Fig.7 Time-domain waveform and frequency spectrum at K1=0.80 令K1=0.20,其他电路参数保持不变,K2以0.003的步长从0变化到1,在电感电流波形峰值处采样,绘制出以K2为参数的分岔图如图8 所示。可以看出,当0 图8 以K2 为参数的分岔图Fig.8 Bifurcation diagram with K2 as parameter 研究表明,当K2取不同值时系统的折叠图与图4类似,时域波形及其频谱图与图5~图7类似,这里不再赘述。 确定控制参数的稳定工作域对系统的设计至关重要。这里保持系统其他参数不变,图9给出了控制参数K1和K2构成的二维平面稳定性边界,曲线下方区域为系统稳定工作域,上方区域为系统不稳定区域。 图9 系统在K2 -K1 平面上的稳定性边界Fig.9 Stability boundary in the space of K2 versus K1 将改进滑模控制与传统滑模控制进行对比,分析改进滑模控制对系统性能的影响。在改进滑模控制下逆变器各参数的稳定区间取值,令K1=0.20、K2= 0.10,传统滑模控制的控制变量为ucon=ae+bsgn(e),a= 0.2,b= 0.1,其他电路参数取默认值。对系统稳定后输出电压的时域波形进行FFT分析可得输出电压uo的频谱图如图10所示。从图10(a)可以看出,传统滑模控制下逆变器输出电压基波分量幅值为97.76 V,THD为1.87%;从图10(b)可以看出,改进滑模控制下逆变器输出电压基波分量幅值为102 V,较传统滑模控制高4.24 V,THD为1.19%,较传统滑模控制低0.68%,奇数低次谐波明显减少。 图10 传统滑模控制和改进滑模控制下逆变器输出电压uo 的频谱图Fig.10 Frequency spectrum of the inverter output voltage uo under conventional and improving sliding mode control 传统滑模控制和改进滑模控制下逆变器输出的有功功率如图11所示,其中实线1、2、3、4分别为传统滑模控制下逆变器输出的基波分量有功功率、直流分量有功功率、2 次谐波有功功率及3 次谐波有功功率,虚线5、6、7、8分别为改进滑模控制下逆变器输出的基波分量、直流分量、2次谐波分量及3次谐波分量的有功功率。可以看出,实线2、3、4和虚线6、7、8 表示输出的有功功率在系统稳定后近似衰减到0,实线1 表示的基波分量有功功率稳定到478 W,虚线5 表示的基波分量有功功率稳定到520 W。通过对比可知,改进滑模控制比传统滑模控制提高了逆变器输出的有功功率,减小了逆变器的损耗。 图11 传统滑模控制和改进滑模控制下逆变器输出有功功率Fig.11 Active power output of inverter under conventional and improving sliding mode control 综上,改进指数趋近律滑模控制提高了系统输出电压的质量及输出功率,其在逆变器控制中有着广泛的应用前景。 令K1=0.20、K2=0.10,研究输入电压E、滤波电感L、开关周期T等外部参数对系统稳定性的影响。 令直流电压E以1 V 的步长从0 V 变化到600 V,其他参数保持不变,绘制出在电感电流峰值处采样的分岔图如图12(a)所示。可以看出,当0 V 图12 其他电路参数的分岔图Fig.12 Bifurcation diagrams of other circuit parameters 令电感L以0.03 mH 的步长从0.3 mH 变化到5.3 mH,其他参数保持不变,绘制出以电感L为分岔参数的分岔图如图12(b)所示。可以看出,随着L的减小,系统从稳定运行经倍周期进入混沌;随着L的进一步减小,系统回到倍周期状态,这一现象称为切分岔。因此,要使系统稳定运行,L的取值应大于4.2 mH。 令开关周期T以1 μs 的步长从100 μs 变化到500 μs,其他参数保持不变,绘制出以T为分岔参数的分岔图如图12(c)所示。可以看出,随着T的增大,系统从稳定运行经倍周期进入混沌,因此要使系统稳定运行,T的取值应小于228 μs。 由上述分析可知,除控制参数外,其他电路参数E、L和T对系统的稳定性也具有重要影响。在实际工程中,要选择合适的参数取值使系统工作在稳定状态。 常用的稳定性理论分析方法有李雅普诺夫指数法和雅可比矩阵法,两者都要求系统的离散数学方程可导。因为改进指数趋近律滑模控制双降压式逆变器的离散模型不可导,所以这两个方法对于本文不再适用。文献[11]提出一种快变稳定性定理,解决了离散数学模型不可导的稳定性判断问题,填补了非线性控制逆变器判断稳定性的空白。为此,本文采用快变稳定性定理进行理论分析。该定理的基本思想是取电流下降段M个开关周期,分别将每个开关周期的占空比和下一个周期的占空比相减后再除以两者差值的绝对值,把计算出的M个数相加即得到稳定系数Q,具体计算公式为 式中,N0为电感电流下降段的某个开关周期。本文取N0=1 825,M=15。 若在M个开关周期内占空比一直保持单调变化,即Q=M时,则系统处于稳定状态;若Q 图13 K1 与E 为参数的稳定性判断结果Fig.13 Results of stability judgment with K1 or E as parameter 本文从非线性动力学角度出发,以双降压式逆变器为研究对象,引入改进指数趋近律滑模控制,建立了系统的离散数学模型,对其进行数值仿真与理论分析,得到了如下结论。 (1)结合分岔图、折叠图、时域波形及其频谱图等分析了不同控制参数下逆变器的非线性行为,确定了控制参数K1和K2的二维稳定工作域。 (2)除控制参数外,给出了其他电路参数E、L、T的稳定工作范围。 (3)利用快变稳定性定理进行了稳定性理论分析。 本文研究结果表明,改进滑模控制提高了逆变器的输出电压质量及输出功率,揭示了改进指数趋近律滑模控制双降压式逆变器的非线性本质,为实际工程中提高逆变器工作稳定性的设计及调试提供了重要的理论依据。1.2 离散模型
2 控制参数对系统稳定性的影响
2.1 控制参数K1 对系统稳定性的影响
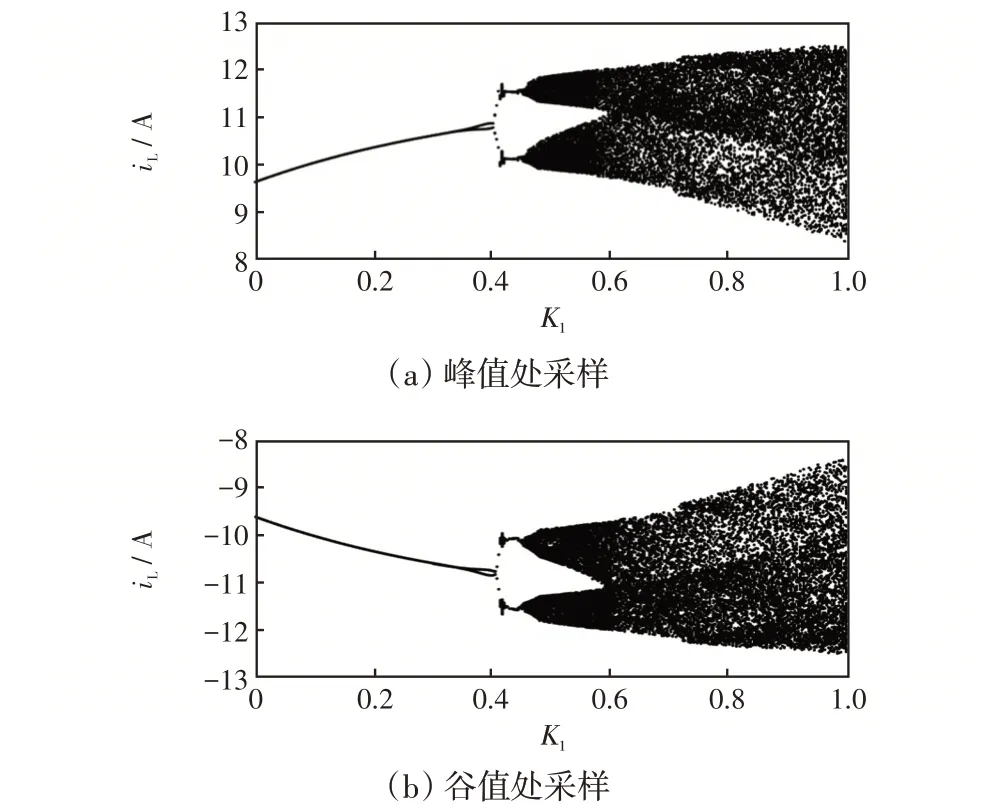
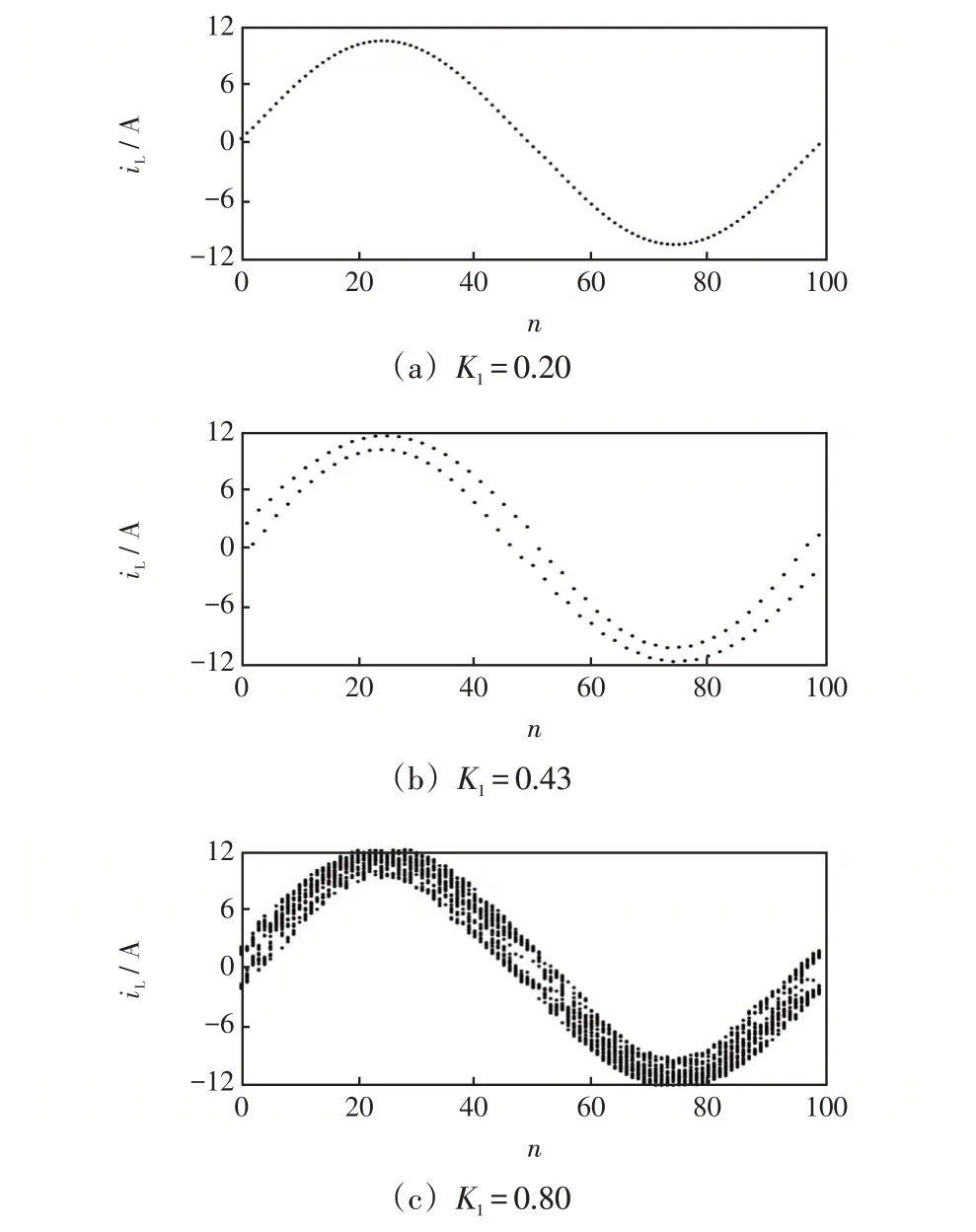
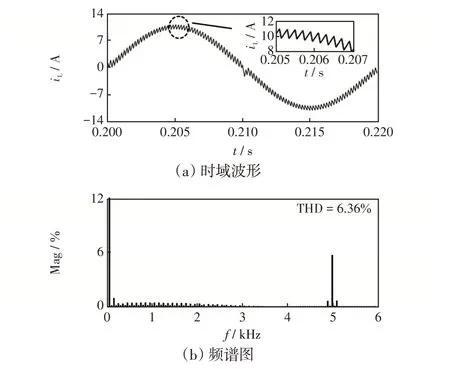
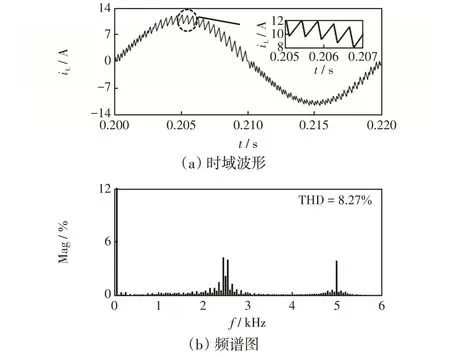

2.2 控制参数K2 对系统稳定性的影响
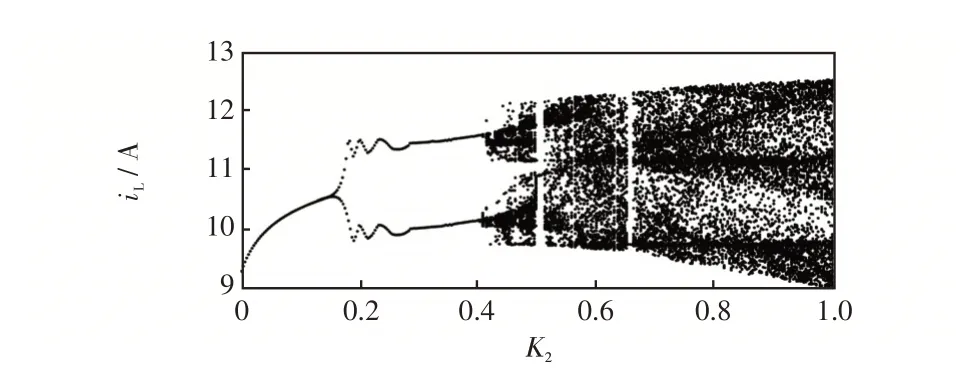
2.3 控制参数的稳定工作域
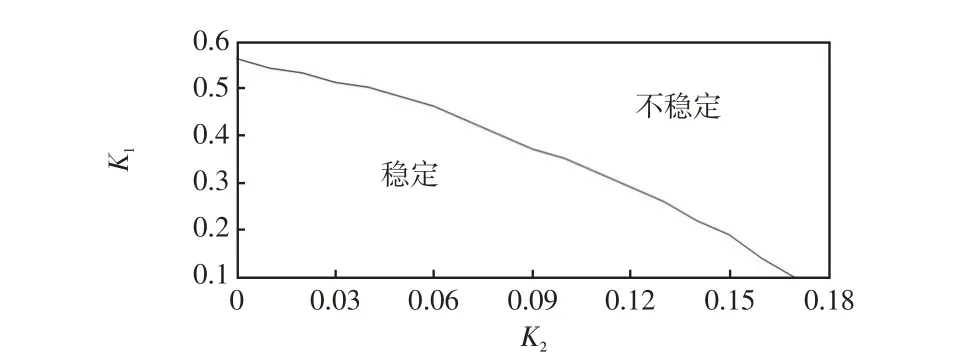
2.4 改进滑模控制对系统性能的影响


3 其他电路参数对系统稳定性的影响
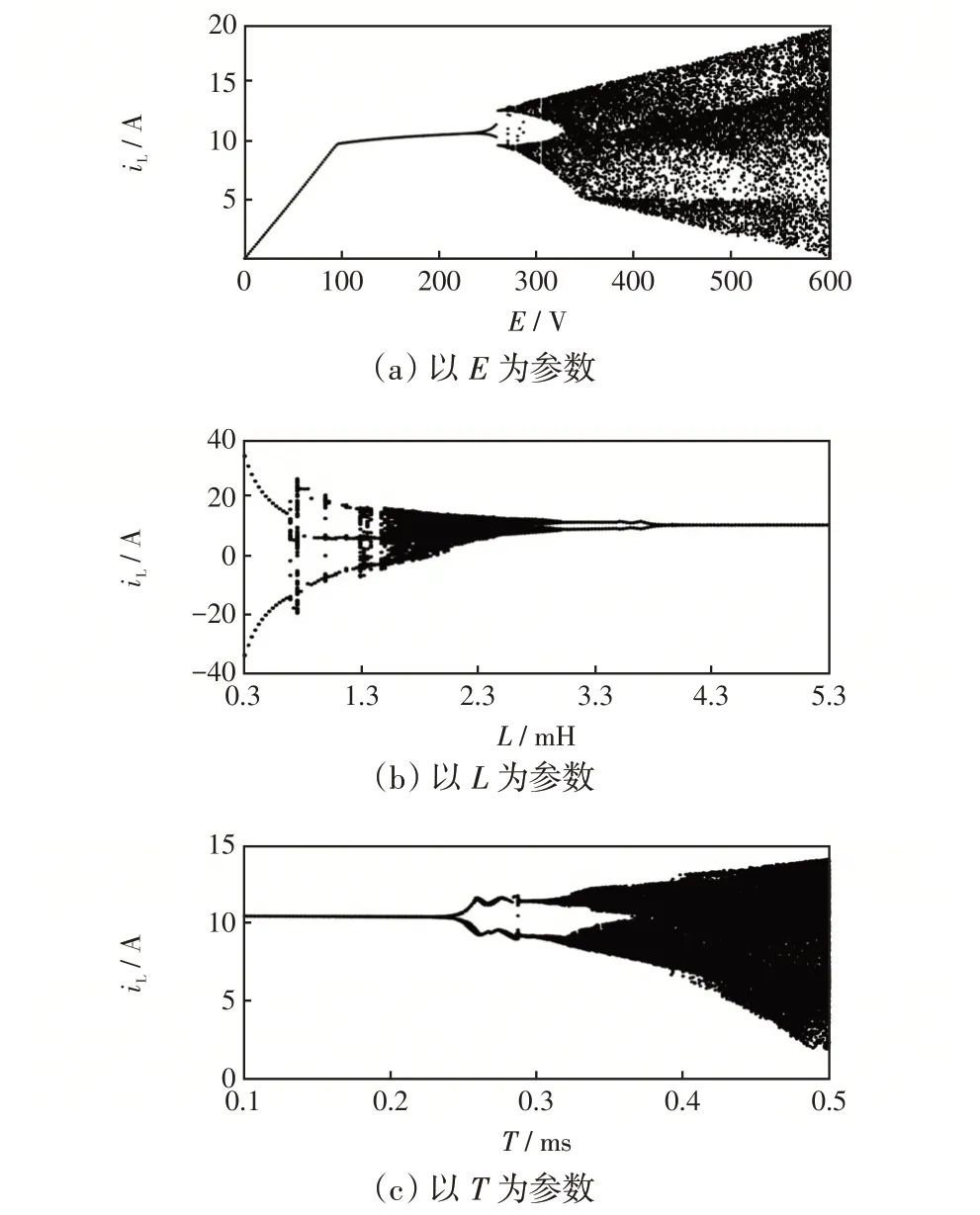
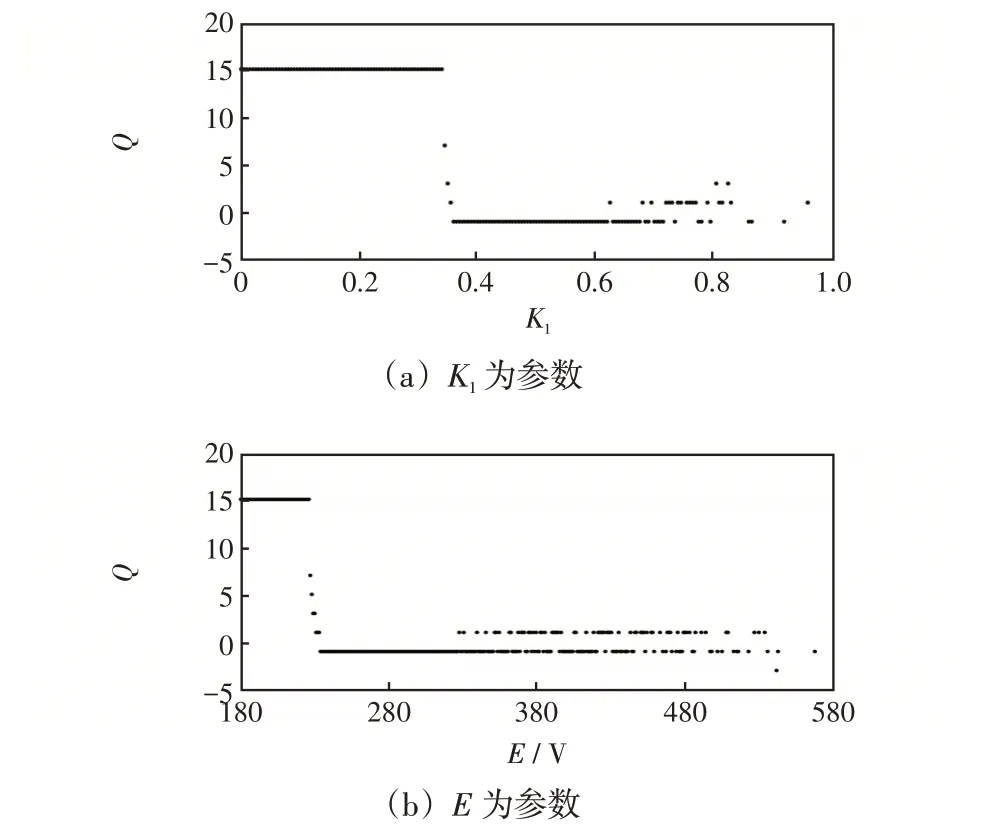
4 稳定性分析
5 结 论

