不平衡数据集异常检测和分类算法

樊 芮，陈湘媛，王冠男，崔艳辉

（1.国网湖南省电力有限公司供电服务中心（计量中心）智能电气量测与应用技术湖南省重点实验室，长沙 410004；2.国网征信有限公司，北京 100055）

异常检测是数据挖掘领域中的一个重要研究方向，目标是从数据集中自动检测和识别出有别于其中大部分数据的异常部分，在生物医学疾病诊断、金融财经欺诈检测、信息安全故障诊断和工业系统入侵检测等领域得到了广泛应用[1-2]。

目前国内外学者对异常检测的研究主要分为基于统计理论的方法、基于聚类的方法、基于分类的方法和基于神经网络的方法4大类。其中，基于统计理论的方法认为自然界中的数据集都可以用某种确定的概率分布模型进行建模，集合中与该模型概率分布不符的数据点即为异常数据[3-4]；基于聚类的方法根据数据集的相关程度将其划分为不同的簇，与簇中心相关程度较小的样本即判决为异常数据，作为一种无监督方法，该类方法不需要训练集，并且原理简单，容易实现[5-7]；基于分类的方法通过挖掘并提取带标签训练数据集内不同类别样本之间的差异性信息，并利用该信息学习得到最优分类函数，从而实现对测试数据类别属性的判断，由于带标签训练样本集的使用，该类方法得到的检测性能通常优于基于聚类的方法[8-12]；基于神经网络的方法是近年来随着人工智能和深度学习技术的发展而兴起的一种新方法，以卷积神经网络、多层感知机等方法为代表，由于具备自适应、自学习和非线性逼近能力，得到了广泛应用[13-14]。

上述研究大都采用单一模型，虽然在面对各自特定问题时获得了较好的结果，但是随着异常检测问题愈加复杂及数据规模愈加庞大，并且实际生产生活中异常检测算法面对的通常是不平衡数据集[15]，上述单一模型会带来许多问题。例如K-均值聚类（K-means）方法的聚类性能对聚类个数的选择依赖性较大[16]，支撑向量机SVM（Support Vector Machine）和神经网络方法在面对不平衡样本时性能会出现下降[17]。可见，单一模型应用存在局限性，将多个模型进行组合应用优势更加明显。

针对上述问题，本文提出一种SVDD-ImSMOTEMICD-K-means组合模型用于实现不平衡数据集条件下的异常数据检测和分类。首先利用正常类样本训练支撑向量数据描述SVDD（support vector data description）分类器构造闭合分类面，从而实现对“异常”数据的检测；然后对“异常”数据进行进一步分析，利用所提的改进少数类样本合成技术ImSMOTE（improved syntheticminority over- sampling technique）对少数类别进行过采样以构建平衡数据集；最后利用所提最大类间-类内距K-均值聚类MICD-K-means（maximization of inter-intra class distance K-means）对“异常”数据进行自动聚类，得到具体的异常数据类别属性。基于加州大学欧文分校UCI（University of California lrivine）公共数据集的实验结果表明，相比于传统方法，所提方法能够获得更高的异常检测和分类性能。

1 算法概述

图1 给出了利用所提组合模型进行异常检测的流程，包含训练和测试2个过程。训练过程的输入数据为正常类样本，利用主成分分析PCA（principal component analysis）进行特征提取和数据降维，进而对SVDD 分类器进行训练得到最优分类面。相对于传统SVM 等分类器，SVDD 只需要正常类样本即可构造闭合分类面，大大降低了训练数据集的构造难度。将测试过程的输入数据分为正常和异常类样本，同样利用PCA对输入数据进行特征提取和数据降维，然后将提取的特征向量作为输入，利用训练阶段得到的最优SVDD 分类面进行异常检测，从而将输入数据自动划分为正常和异常两类，至此完成了算法的第1 阶段，即基于SVDD 的异常数检测。第2 阶段为基于MICD-K-means 的异常数据分类，首先利用所提ImSMOTE 对样本集中少数类别进行过采样以获得均衡数据集；然后利用MICD-K-means 算法对异常数据进行聚类分析，自动将其聚集为K个类别，从而实现异常数据类别属性的区分。

图1 本文所提方法流程Fig.1 Flow chart of proposed method

2 基于SVDD 的异常数据检测

2.1 基于PCA 的数据降维

异常检测问题的多样性和复杂性决定了研究人员通常会面临高维、非线性和海量数据的处理需求，可能产生维数灾难问题。同时，数据中往往还存在着大量重复、冗余信息，不仅会降低算法运行效率，还会影响检测性能。因此，在进行异常检测前通常需要对高维数据进行降维处理。

PCA 是数据分析领域中一种经典的数据降维和特征提取方法，通过线性变换将原始数据中具有相关性的信息进行组合得到少量相互正交的综合性特征，这些综合性特征即为主分量。对于任意D维观测数据s=[s1,s2,…,sD]T，利用PCA 进行数据处理的主要步骤如下。

步骤1协方差矩阵计算，其计算公式为

式中：R为观测数据的协方差矩阵；E( )表示期望运算；u为观测数据s的均值；上标H 表示矩阵复共轭运算。

步骤2特征值分解。对协方差矩阵R进行特征值分解，从而得到特征值和特征向量，即

式中：λi和vi分别为协方差矩阵的特征值和特征向量，且λ1≥λ2≥…≥δ2=…=δ2，δ2为噪声方差；W为主分量个数。

步骤3根据能量占比大的特征值个数来确定主分量。将占特征值总能量90%的大特征值对应的特征向量作为主分量，其计算公式为

步骤4子空间投影实现数据降维。将原始数据投影到步骤3 得到的主分量张成的子空间中以实现数据降维，即

式中，为PCA降维后的数据。

2.2 基于SVDD 的异常检测

对于自然界的过程，正常是一种长期且稳定的状态，异常是暂时且随机的状态。在采用分类方法进行异常检测时，通常难以获得足够多的异常样本用于模型训练，而SVDD分类器只需要正常类样本即可构造闭合覆盖模型，从而实现对未知样本的判断。因此，本文选用SVDD分类器进行异常检测，实现对测试样本正常或异常的类别判决[18]。

设给定的正常类训练样本集Xti=[xt1,xt2,…,xtN]T，其中xtN为Xti中的第N个样本。SVDD基于闭环超球体的分类问题可以利用如下优化函数进行描述：

式中：c和r分别为超球体的球心和半径；ξi和C分别为松弛变量和惩罚因子。当训练样本集在原始空间中不符合球状分布时，SVDD 通过核函数将其映射到高维空间进行分析。目前常用的核函数为高斯核函数，可以表示为

式中：K(xti,xtj)为高斯核函数；σ为高斯核参数，σ的取值决定着超球体边界的紧密性。在高维空间中，结合拉格朗日乘子和核函数可以将式（5）转换为如下的对偶形式：

式中，α′i为xti对应的指示参数。当α′i>0 时，xti为最优超球体上的支撑向量，利用所有支撑向量可以计算得到最优超球体的球心c和半径r为

式中，‖ ‖2表示欧式距离算子。式（8）即为最优SVDD 分类面的表达式。在测试阶段，对于任意未知测试样本x*，SVDD的决策方程为

若f(x*)≤0，则表明x*处于超球体内部，将其判决为正常类样本；若f(x*)>0，则x*处于超球体外部，将其判决为异常类样本。

3 基于MICD-K-means 的异常数据聚类

3.1 ImSMOTE 过采样

根据图1 所示流程，在基于SVDD 分类器实现正常类和异常类样本分类后，需要进一步对异常类样本进行分析，将其划分为不同的聚类。由于异常数据通常呈现出典型的样本不平衡现象，如果直接对不平衡样本集进行分类，多数类样本会模糊少数类样本的边界，在类别重叠区域，分类器会将大部分少数类样本判决为多数类样本以得到较低的误分率。为了解决该问题，通常对少数类样本进行过采样以构建平衡数据集[19]，SMOTE是其中的经典方法。该算法通过随机选择少数类样本并在其与近邻样本之间插入多个合成样本的方式，生成无重复的新的少数类样本以实现数据集均衡。

SMOTE 算法具有原理简单、容易实现等优点。但是在实际应用中，只有分布在不同类别样本集合边界处的数据才会对分类结果产生影响，在样本集内部的数据不但对分类结果影响较小，反而会增加算法运算复杂度[20]。基于此，本文对SMOTE算法进行改进，只对少数分布在数据集边界的样本进行过采样操作，使得合成后的数据集兼顾分类性能和运算效率。本文所提的ImSMOTE算法步骤如下。

步骤1近邻样本计算。对少数类数据集中每个样本hi，根据欧式距离由近及远关系确定其k近邻样本集。

步骤2判断是否为边界点。对样本hi的k近邻样本集中的样本比例进行分析，若集合中多数类样本比例高于少数类样本比例，则将hi判定为边界样本，否则将其放回少数类样本集。

步骤3对边界样本集进行过采样。对步骤2得到的边界样本集进行过采样操作，合成新的样本hnew。过采样操作需满足如下关系式：

式中：hj为边界样本集中根据过采样倍数n随机选取的样本；rand( )1 表示[0,1]范围内的随机数。

步骤4重复步骤1～步骤3，直至构建满足数量要求的均衡样本集。

3.2 MICD-K-means 聚类

K-均值聚类作为一种经典的无监督聚类方法，用样本之间欧式距离的大小来衡量样本相似程度，从而将距离近的样本划分为同一子集实现数据聚类，具有简单高效的优点。采用K-均值聚类时首先需要确定聚类个数，常用方法是根据先验信息进行设置，但存在主观性强和适应性差的问题，并且实际中很多应用场景都无法获得先验信息。针对该问题，本文提出MICD-K-means方法，对异常数据进行自动聚类，提升算法的自动化程度和适应性。具体步骤如下。

步骤1设置类别数K=1。

步骤2从数据集中随机选择K个样本g1,g2,…,gK作为初始聚类中心。

步骤3计算每个样本到K个聚类中心的欧式距离，并将其划分至与其距离最近聚类中心对应的子类中。样本fi到聚类中心gj的欧式距离可以表示为

步骤4对K个子类的聚类中心进行更新，更新公式为

式中，nk为第k个子类的样本数。

步骤5按K个新聚类中心对样本进行重新划分，若连续两次得到的划分结果一致，则算法收敛，否则重复步骤3～步骤5。

步骤6计算算法收敛后的类间-内间距rK，其计算公式为

步骤7K=K+1，转至步骤2。

步骤8将K=1,2,…,n遍历，得到r1,r2,…,rn。选择最大类间-内间距对应的类别数K作为最终的聚类个数。

4 实验及结果分析

4.1 实验数据

为了验证所提异常检测算法在实际工程应用中的性能，采用KDD CUP’99入侵检测标准数据集开展验证实验。KDD CUP’99是MIT林肯实验室和美国国防高级研究计划局合作建立的入侵检测系统录取的tcpdump 数据，被广泛应用于工业系统异常入侵检测领域。该数据集包含1 类Normal（正常）数据及DoS（拒绝服务攻击）、R2L（远程非授权访问）、U2R（非法获得超级用户权限）、Probe（探测和扫描）4类攻击数据。，每条数据由41维网络包基本信息特征构成。表1 给出了每种数据类别对应的样本分布情况，可以看出，该数据集中样本分布极不均衡，DoS类异常数据占总数据的80%以上，而U2R和R2L两类数据分别只有52和126条记录。

表1 KDD CUP’99 数据集数据分布Tab.1 Data distribution of KDD CUP’99 data set

4.2 评估指标

目前，对异常检测算法进行评估通常采用异常检测结果混淆矩阵，如表2所示。根据异常检测结果混淆矩阵可以计算得到准确率和误检率等评估指标。

表2 异常检测结果混淆矩阵Tab.2 Confusion matrix of abnormal detection results

由于本文所提方法在常规异常检测基础上进一步具备了异常数据类别属性判断，即分类能力，异常检测结果混淆矩阵（见表2）已不能全面衡量多类分类时不同方法的性能，因此本文对异常检测结果混淆矩阵进行扩展得到异常检测及分类结果混淆矩阵，如表3 所示，其中TPi_P 为将实际第i类数据判决为第i类标签的样本数，TPi_N 为将实际第i类数据判决为其他K-1类标签的样本数。

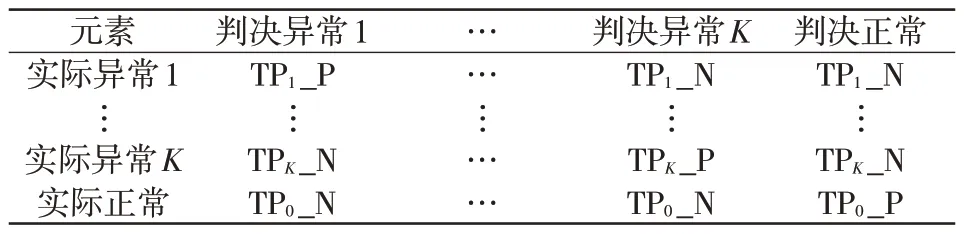
表3 异常检测及分类结果混淆矩阵Tab.3 Confusion matrix of anomaly detection and classification results

在异常检测及分类结果混淆矩阵的基础上，定义每种类别分类的正确率（ACC）和所有类别分类的平均正确率（ACC_MEAN）两项指标对所提方法的异常检测与分类性能进行定量评估。其中，每种类别分类正确率为该类别正确分类样本数除以该类别样本总数；所有类别分类的平均正确率为所有正确分类样本数除以总样本数，可分别表示为

4.3 数据降维

根据图1所示流程，首先采用PCA 方法对输入数据进行降维处理。图2 给出了PCA 分解后得到的输入数据特征值谱图，可以看出，从序号为8 的特征值开始，对应的归一化特征值已接近于0。根据式（3）可以计算得到能量占比大的特征值个数为3。表4 给出了3 个能量占比大的特征值对应主分量之间的相关系数，可以看出，3 个主分量（PC1～PC3）之间及3个主分量与剩余特征向量之间的相关系数均很小（小于10-6），这表明特征之间几乎不存在冗余重复信息，有效实现了数据降维。

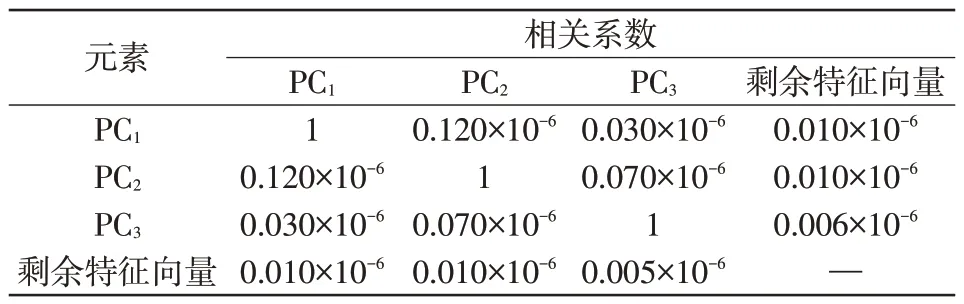
表4 不同主分量之间的相关系数Tab.4 Correlation coefficients between different principal components

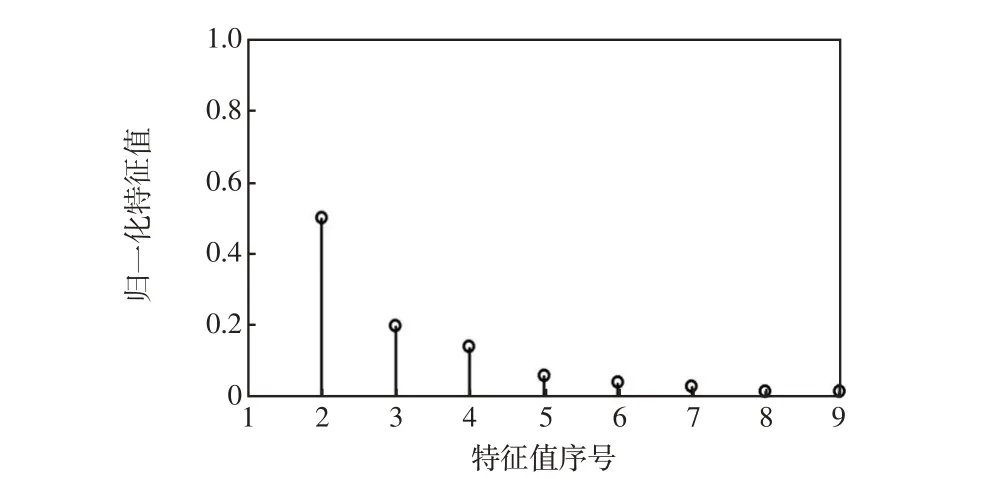
图2 特征值谱图Fig.2 Eigenvalue spectrum

4.4 样本均衡及MICD-K-means 聚类个数确定

利用所提ImSMOTE 方法对U2R 和R2L2 类异常数据进行过采样处理，以实现样本均衡。根据表1所示每种类别样本数量，对U2R类样本和R2L类样本进行50 倍过采样，使样本均衡后两类样本数据分别为2 600 和6 300。在完成样本均衡后，根据MICD-K-means 方法得到类内-类间距变化曲线如图3 所示，可以看出，当K=4 时类间-类内距最大，则将所提方法自动确定聚类个数K为4。

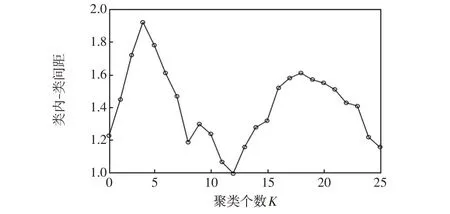
图3 类间-类内距随K 变化曲线Fig.3 Variation curve of inter-intra class distance with K

4.5 异常检测及分类结果

根据图1 所示流程，在完成PCA 降维后，首先需要利用SVDD 分类器进行正常或异常类列判决，因此实验中取70%的正常样本作为训练数据集建立最优SVDD 分类面，对剩余30%正常样本和所有异常数据（4 类异常数据被归为1 类）进行判决，SVDD 核参数采用五折交叉验证的方式进行寻优。表5给出了判决结果混淆矩阵，可以看出，SVDD在实现对所有异常样本正确判决的同时，仅仅将少量正常样本（13组）判决为异常，有效实现了异常检测。

表5 SVDD 异常检测结果混淆矩阵Tab.5 Confusion matrix of SVDD anomaly detection results

对表5 判决为异常的数据利用MICD-K-means得到的聚类结果如图4 所示。为了直观展示聚类结果，图4 给出了4 类类异常数据边界处部分数据的二维平面投影结果，可以看出，每类异常数据在二维平面均表现出了较高的聚集性，且4类异常数据之间又呈现出了较高的差异性。

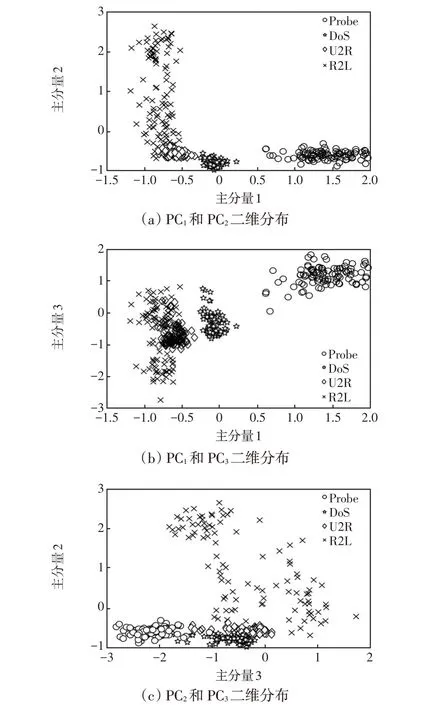
图4 MICD-K-means 聚类结果二维平面投影Fig.4 Two-dimensional plane projection of MICD-Kmeans clustering results

对图4 和表5 所示结果进行综合分析，得到本文所提异常数据检测及分类结果混淆矩阵，如表6所示。同时为了对比，表7 和表8 分别给出了在相同条件下采用多步多分类器MSMT（multi-step and multi-type classification）[13]和长短时记忆神经网络LSTM（long short term memory）[14]进行异常检测及分类得到结果混淆矩阵，其中MSMT 分别采用SVM、决策树和B-Bagging3 种分类器按步骤逐步实现对DoS、Probe、Normal、U2R和R2L的检测。图5给出了不同方法异常检测性能对比。对表5～表8及图5所示结果进行对比分析可知，3 种方法对Normal、Probe 和DoS3 类数据得到的分类正确率较为接近，其中LSTM 和MSMT 两种方法对3 类数据的正确分类率均高于97%，所提方法对3 类数据的正确分类率高于99%，但是由于LSTM没有进行样本均衡，对U2R 和R2L 两类数据的正确分类概率分别只有61.5%和60.3%。进一步对表7进行分析可知，为了获得更高的平均正确分类率，在模型训练过程中LSTM将大部分U2R类和R2L类数据判决为数据更多的DoS类和Probe类数据。由表8可知，MSMT对U2R 类数据的正确分类概率达到80.7%，对R2L 类数据的分类正确概率为76.2%，相比于LSTM 有一定提升，但是MSMT在对U2R和R2L两类数据的判决中出现了混淆，将大部分R2L类数据判决为U2R类数据，导致性能出现下降。由图5 可知，所提方法对U2R 和R2L 两类数据的平均正确分类率高于96%，相对于LSTM 和MSMT 方法分别提升了30%以上和15%以上，性能优势明显，验证了所提方法的有效性。

表6 所提异常检测及分类结果混淆矩阵Tab.6 Confusion matrix of the proposed anomaly detection and classification result

表7 LSTM 异常检测及分类结果混淆矩阵Tab.7 Confusion matrix of LSTM anomaly detection and classification results

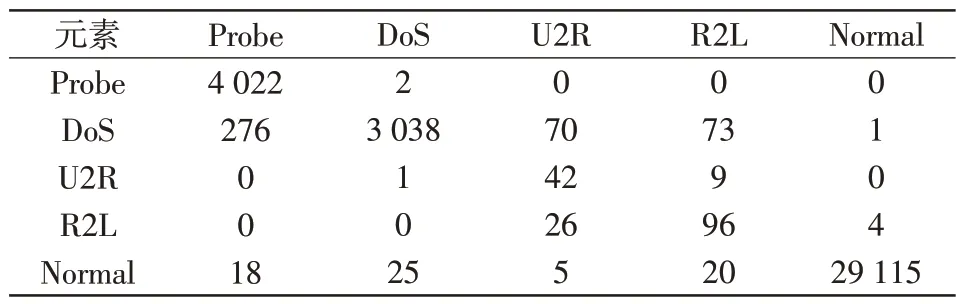
表8 MSMT 异常检测及分类结果混淆矩阵Tab.8 Confusion matrix of MSMT anomaly detection and classification results

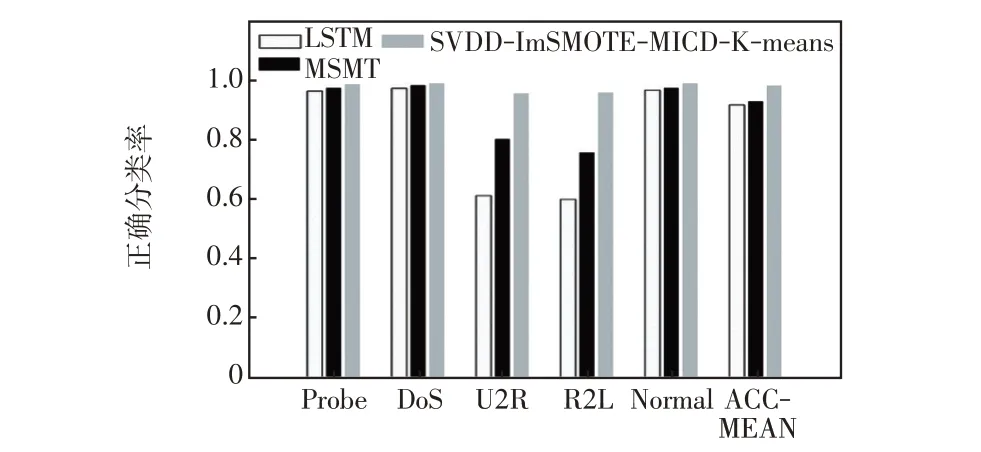
图5 不同方法异常检测性能对比Fig.5 Anomaly detection performance of different methods

接收机工作特性ROC（receiver operating characteristic）曲线及接收机工作特性曲线下面积AUC（area under ROC curve）被广泛应用于评估分类模型的性能。ROC曲线最初用于评估两类分类问题，对于多类分类问题，可以将其转化为多个两类分类问题，即除正类外其他都作为负类，然后分别构建多条ROC 曲线，最后通过对多条ROC 曲线取平均的方式得到最终的ROC曲线。

图6 给出了对不同方法进行评估得到的ROC曲线，其中横坐标为根据分类结果计算得到的虚警概率FPR，纵坐标为对应的检测概率TPR，可以看出，所提方法的ROC 曲线更靠近于平面的左上方，AUC 值（0.892 4）明显大于MSMT（0.824 7）和LSTM（0.802 5），这表明所提方法具有更好的分类性能。

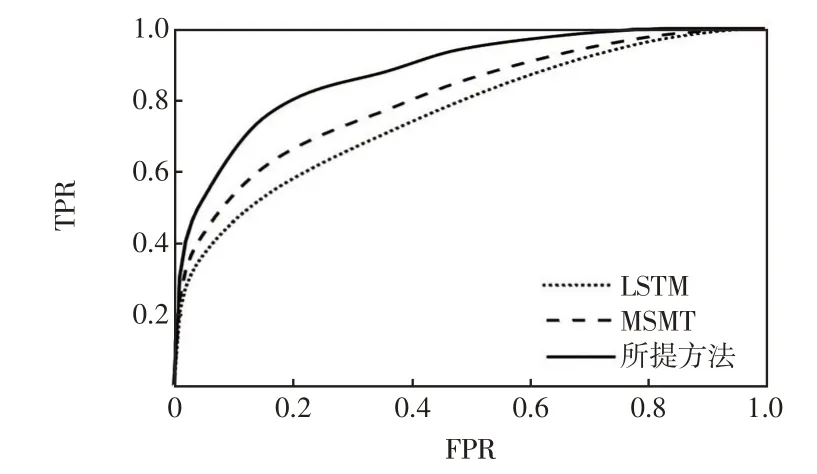
图6 不同方法的ROC 曲线Fig.6 ROC curves of different methods

数据采集和存取过程中通常会引入噪声分量，因此异常检测算法在低信噪比条件下仍能获得较好的性能。通过加入高斯白噪声构造低信噪比为0 dB的实验数据来验证所提方法的泛化能力。图7给出了低信噪比条件下不同方法的对比结果，可以看出，低信噪比条件下所提方法对每类数据的分类性能仍明显优于LSTM 和MSMT。对比图5 和图7可以看出，信噪比降低后LSTM 和MSTM 的ACC_MEAN 指标分别下降了17.7%和13.5%，而所提方法的ACC_MEAN 指标仅下降6.2%，这表明所提方法具有较高的噪声鲁棒性，对低信噪比数据具有较强的泛化能力。

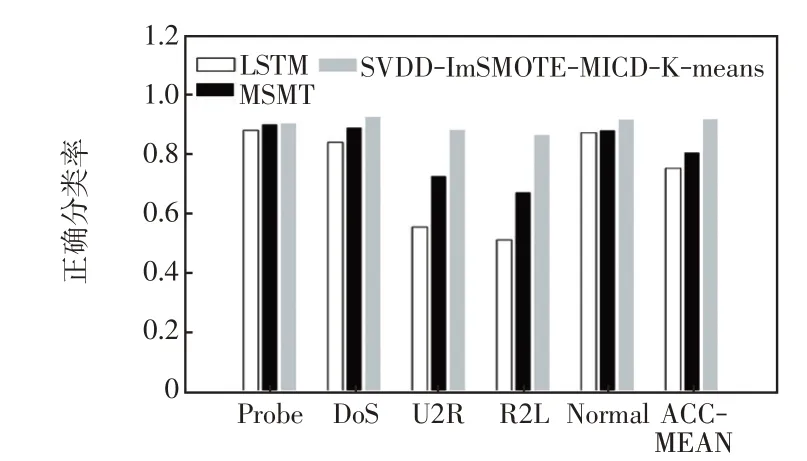
图7 低信噪比条件下不同方法异常检测性能Fig.7 Anomaly detection performance of different methods at low signal-to-noise ratio

为了进一步验证所提方法对不同数据的泛化能力，采用某地区异常用电实测数据集开展实验，该数据集包含正常用电、窃电、漏电和计量错误4类数据。图8 给出了不同方法异常用电实测数据检测性能，可以看出，与前述实验类似，所提方法对每类数据均能获得最优的分类性能，相比于LSTM和MSMT，所提方法的ACC_MEAN 分别提升了13.3%和8.5%，这表明所提方法比LSTM 和MSMT具有更强的数据适应性和泛化能力。

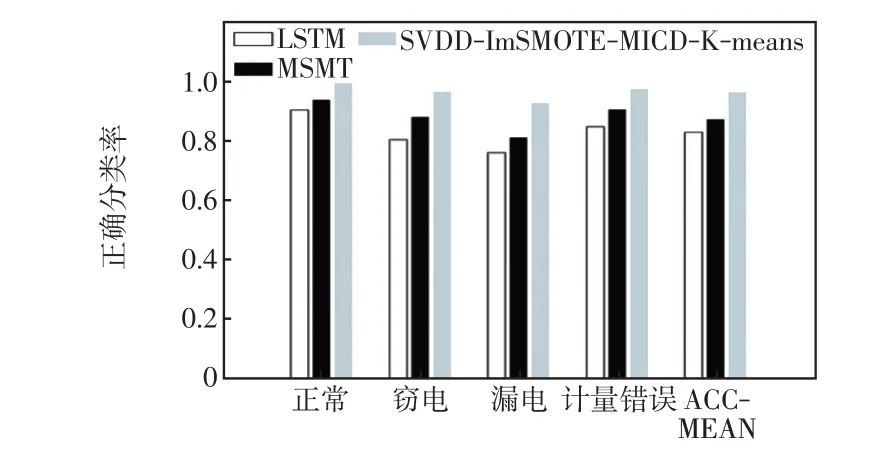
图8 异常用电实测数据检测性能Fig.8 Detection performance based on measured data of abnormal power consumption

5 结 论

针对单一模型进行异常检测的局限性及不平衡样本导致的检测性能下降问题，本文提出一种SVDD-ImSMOTE-MICD-K-means 组合模型用于实现不平衡样本集条件下的异常数据检测和分类。主要结论如下。

（1）提出了ImSMOTE 方法用于对少数类样本进行过采样以构建平衡数据集，ImSMOTE 有效解决了SMOTE重复采样和无效采样的问题。

（2）提出了MICD-K-means 方法对异常数据进行自适应聚类，相比于K-means 方法，MICD-Kmeans 方法能够自动确定聚类个数，提升算法的自动化程度并降低运算复杂度。

（3）提出了一种先分类后聚类的层次化异常检测方法，在有监督SVDD 分类器实现异常检测的基础上，利用无监督MICD-K-means 方法对异常数据进行聚类，得到异常属性，以达到数据的精细化管理。

（4）所提方法相比于传统方法能够获得更高的检测性能，特别是能够明显提升少数类样本的分类性能，可以更好地满足实际工程应用需求。