基于改进超螺旋算法的永磁同步电机快速积分终端滑模速度控制

南宇洋，朱其新，2，刘红俐，朱永红

(1.苏州科技大学机械工程学院，江苏苏州 215009；2.苏州科技大学江苏省建筑智慧节能重点实验室，江苏苏州 215009；3.景德镇陶瓷大学机电工程学院，江西景德镇 333001)

0 前言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)具有结构简单、运行可靠、体积小、质量轻等特点，随着近年来永磁材料的发展以及永磁电机技术的完善，永磁同步电机在各个领域用途广泛。不过永磁同步电机是一个强耦合、非线性的系统[1-3]，对内部参数扰动和外部干扰极其敏感，因此传统的线性控制方法很难取得满意的控制效果。

滑模控制(Sliding Mode Control，SMC)是一种变结构控制，不同于传统的线性控制，它拥有非线性、对扰动具有强鲁棒性的特点[4]，非常适合用在永磁同步电机的控制上，是当今的研究热点。滑模控制的设计中滑模面的设计通常为第一步。早期的线性滑模面[5]使得系统状态满足渐进收敛，之后ZAK[6]提出了终端因子，进而提出了终端滑模面，把渐进收敛发展到有限时间收敛，到后来的非奇异终端滑模面[7]对终端滑模面的奇异性进行修正，以及最近提出来的积分终端滑模面[8]，在保留了终端滑模面的特点后加入积分滑模面改善了稳态误差。此外全局鲁棒滑模面[9]使得系统状态从一开始就在滑模面上，使得全局鲁棒成为可能。

不过SMC控制最大的问题就是抖振问题[10]。为了解决这个问题，国内外学者进行了大量的研究，归纳起来，主要有以下几种方法：第一种方法是用边界层法去抖振，边界层方法抑制抖振主要是在滑模面设置一个边界从而减小抖振，但是却降低了鲁棒性[11]；第二种方法是用高阶滑模的控制方法进行抑抖，主要是通过把易造成抖振的切换项放进控制器的导数中[12]，最终求得的控制器是连续的从而减少了抖振。目前一般认为超螺旋算法是应用最广的高阶滑模。文献[13]将自适应控制与超螺旋算法结合，提高了系统的鲁棒性和静、动态性能；文献[14]采用非奇异快速终端滑模面与改进的超螺旋算法，设计出的自适应非奇异快速终端二阶滑模控制器削弱了抖振以及抵消了干扰；文献[15]设计改进快速终端二阶滑模控制器，使得系统的抖振得到进一步削弱，并且快速性得到增强。

本文作者受文献[16]的启发，在广义超螺旋控制的基础上，与积分滑模进行组合，设计出的控制器使得系统的动态、稳态特性得到进一步的提高，抖振的幅度也得到了进一步的减小。

1 PMSM数学模型

在建立永磁同步电机数学模型时，为了简化分析，做如下假设[17-19]：(1)忽略电机定子铁心饱和，电感参数恒定不变；(2)转子永磁材料电导率为0；(3)不计铁心涡流和磁滞损耗；(4)转子没有阻尼绕组；(5)电机定子中的电流为三相对称正弦波形；(6)不考虑电机周围环境温度对电机的影响。

基于以上假设，定子电压在dq轴可表示为

ud=Ldpid+Rsid-ωrLqiq

(1)

uq=Lqpiq+Rsiq+ωrLdid+ωrψf

(2)

转矩方程可表示为

Te=np[ψfiq+(Ld-Lq)idiq]

(3)

运动方程可表示为

(4)

其中：ud、uq分别为定子电压的交、直流分量；id、iq分别为定子电流的交、直流分量；p为微分算子；Ld、Lq分别为d、q轴的电感；Rs为定子电阻；ωr为电角速度；np为极对数；Te为电机转矩；TL为负载转矩；B为摩擦系数；ψf为转子永磁体磁链。

现取状态变量为

(5)

其中：

eω=ωref-ωr

(6)

2 基于广义超螺旋算法的积分终端滑模变结构控制器

选择传统积分终端滑动模切换函数：

(7)

式中：c、f>0为滑动模系数；λ为比1小的正分数。

(8)

考虑到Ld=Lq，采用id=0控制策略，式(3)可简化为

Te=npψfiq

(9)

由式(4)(5)(7)(9)得

(10)

(11)

设计滑模变结构控制律为

iq=iqeq+iqll

(12)

其中：

(13)

iqll设计为广义超螺旋型

(14)

则可得

(15)

为了减少抖振，可替换符号函数为sat函数[20]。

3 基于改进的广义超螺旋算法的积分终端滑模变结构控制器设计

对于滑动模切换函数(7)，重新设计如下

(16)

其中：c1、c2、θ为大于0的待设计常数。

对式(16)求导再结合(5)、(9)得

(17)

设计滑模变结构控制律为

iq2=iqeq2+iqll2

(18)

其中：

(19)

iqll2设计为改进广义超螺旋型：

(20)

则可得

(21)

下面证明该算法的稳定性。

设计李雅普诺夫函数

(22)

对式(22)进行求导，得

(23)

式(23)先不考虑d的影响可得

(24)

α4≥c1d

(25)

则有

(26)

则系统是渐进稳定的。为了减少抖振，可替换符号函数为sat函数[20]。

4 仿真分析

仿真工具选用MATLAB/Simulink，PMSM相应参数如表1所示，逆变器开关频率为15 kHz，控制周期为10 μs。

表1 PMSM参数

图1和图2分别为在iq和iq2控制作用下的电机转矩变化图。可以看出：改进的超螺旋算法对于抖振的抑制作用更加明显。

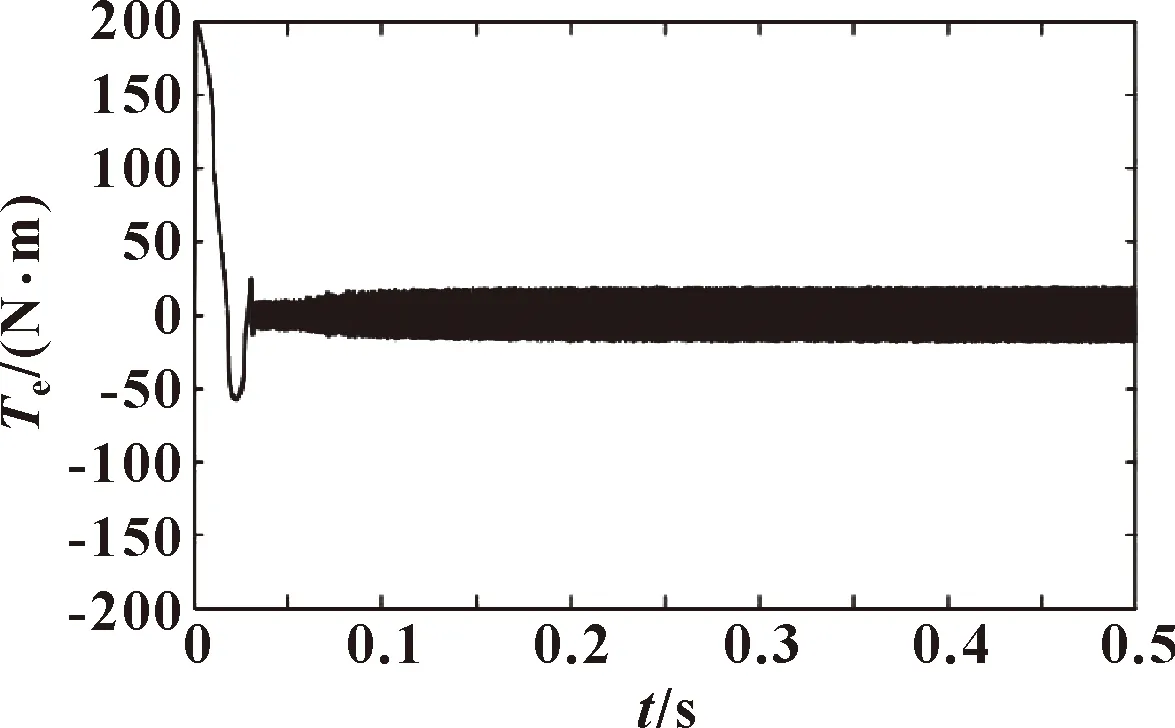
图1 iq作用下的Te变化曲线

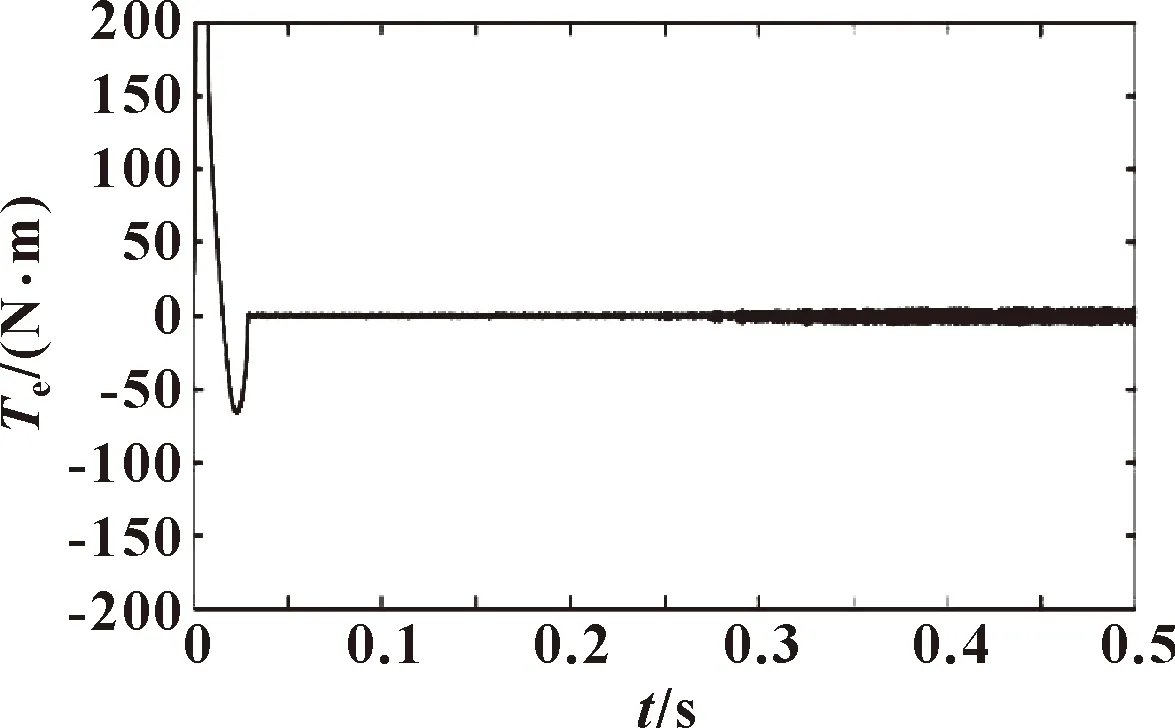
图2 iq2作用下的Te变化曲线

图3和图4为滑模面的变化曲线，可以看出新设计的滑模面抗抖振性能更好，且收敛速度和原来相当。

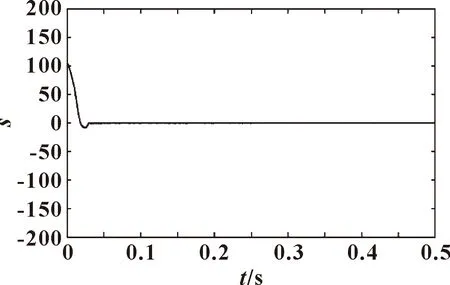
图3 iq作用下的s变化曲线

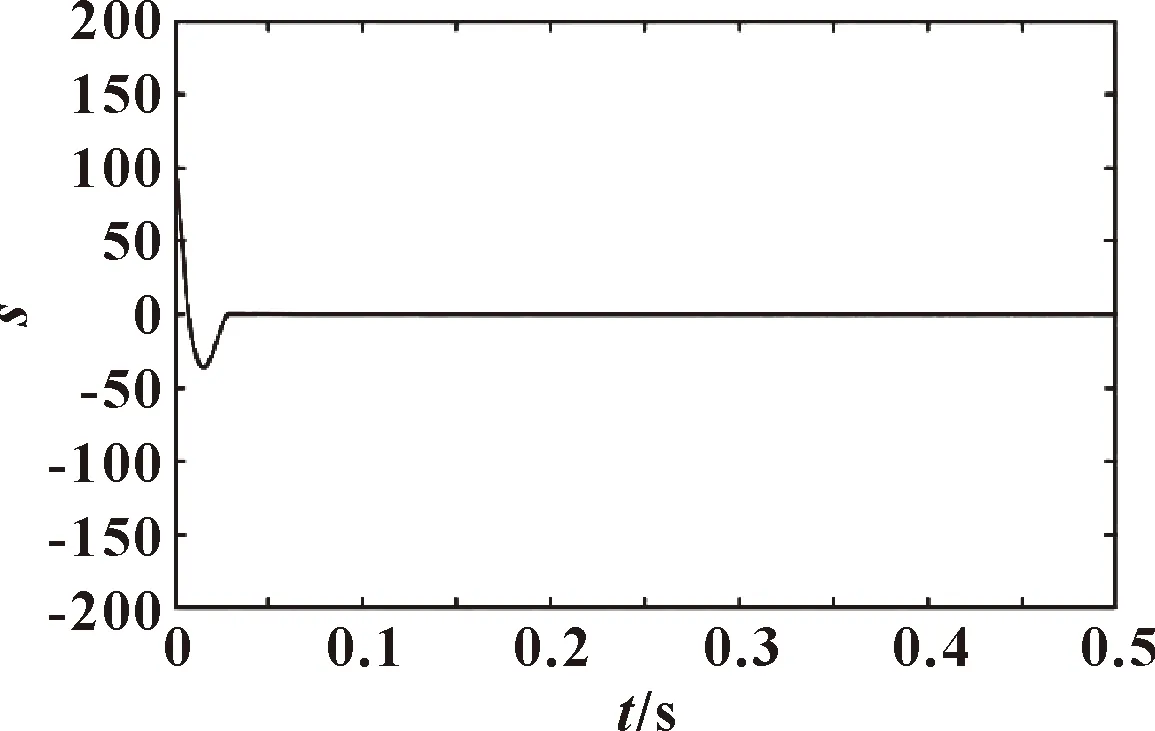
图4 iq2作用下的s变化曲线

在0.2 s加入5 N·m负载转矩TL，iq、iq2变化曲线分别如图5 、图6所示，设计的控制器相比于传统的控制器具有更好的抗抖振能力。

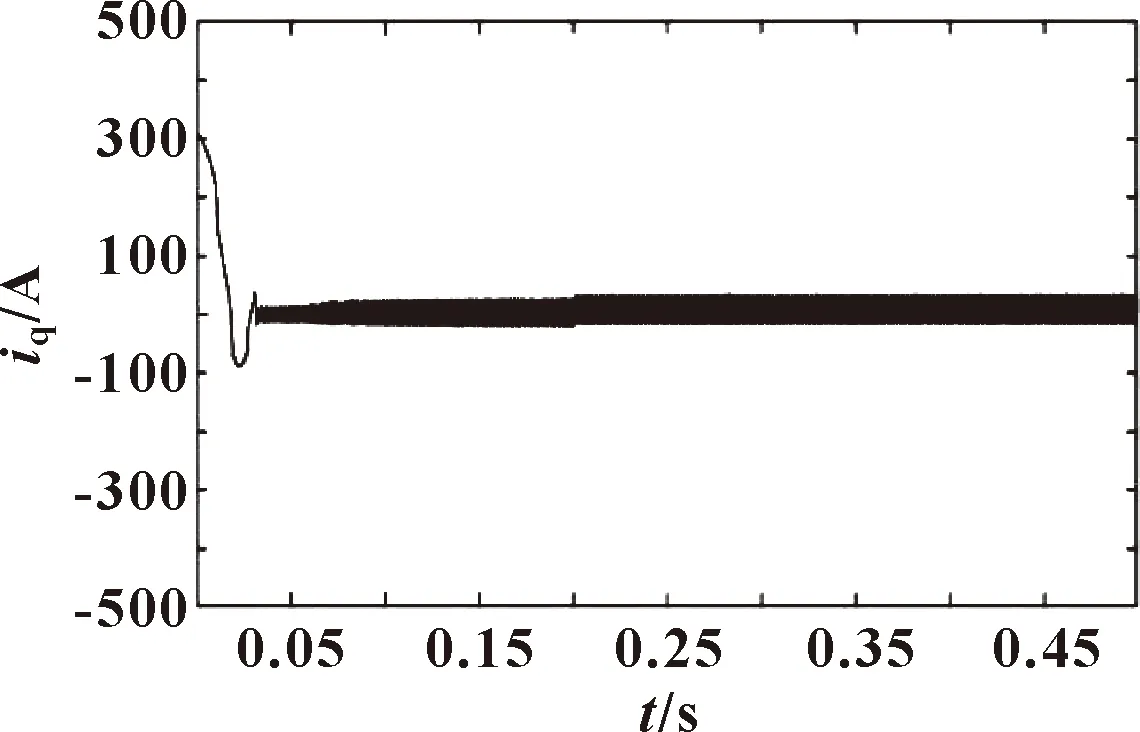
图5 加入负载扰动下iq变化曲线

图6 加入负载扰动下iq2变化曲线

如图7 、图8所示，加入扰动后，电机转矩在新控制器的作用下抖振依然较小，传统控制器下的电机转矩还是有较大的抖振。

图7 加入负载扰动下传统控制器的Te变化曲线

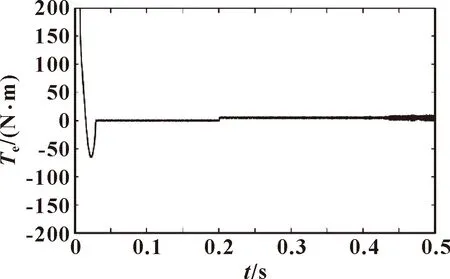
图8 加入负载扰动下新控制器的Te变化曲线

仿真结果表明：基于改进超螺旋算法的永磁同步电机系统运行正常，转矩和转速控制效果良好，电机平稳运行，与传统的广义超螺旋算法对比控制抖振和抗扰动能力都有提高。

5 结论

通过分析传统的基于超螺旋算法的永磁同步电机快速积分终端滑模速度控制易受扰动影响以及处理抖振能力较弱的特点，设计了改善的滑模面以及超螺旋控制器，通过分段滑模面的设计，使抖振得到明显的减小，超螺旋控制器的设计加入了线性项以及终端因子，使系统的动态特性得到进一步的提高。仿真结果表明：改进的滑模控制有着更强的鲁棒性和抗抖振能力，后续可以对扰动进行一个估计从而提高系统的抗扰动能力。