双金属温度计的测量不确定度评定
高旭辉 李姣姣 杨超 刘浩然 王艳

摘要:文中按照JJF1059.1-2012《测量不确定度评定与表示》的要求,对工作用双金属温度计100℃温度点校准结果的不确定度分量进行分析,对典型测量不确定度进行评定,并提出提高测量准确度的方法。
关键词:双金属温度计;校准;不确定度
Evaluation of Measurement Uncertainty for Bimetallic Thermometers
GAO Xuhui, LI Jiaojiao, YANG Chao, LIU Haoran, WANG Yan
(Shanxi Institute of Metrology Science, Xi?an 710100, Shanxi, China)
Abstract: According to the requirements of JJF1059.1-2012, the uncertainty components of the calibration result of the working bimetallic thermometer at 100℃temperature point are analyzed, the typical measurement uncertainty is evaluated, and the methods to improve the measurement accuracy are put forward.
Key Words: Bimetallic thermometer; Calibration; Uncertainty
0引言
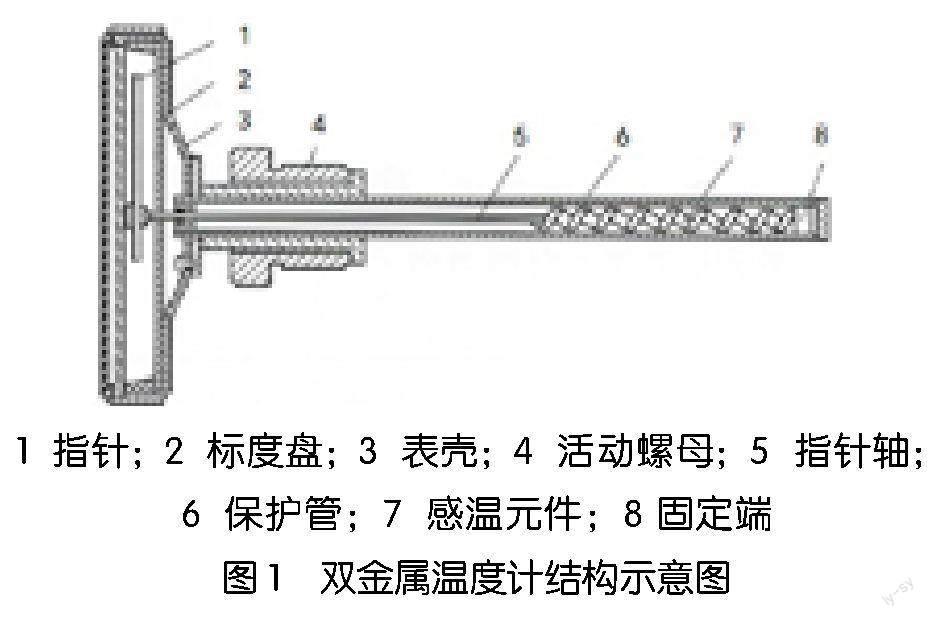
双金属温度计是一种适合中、低温测量的温度仪表,它是利用膨胀系数不同的两种纯金属片或合金片牢固结合在一起形成感温元件,一般绕制成螺旋形,其一端固定,另一端(自由端)装有指针。其结构如图1所示。
当温度变化时,感温元件曲率发生变化,自由端旋转,带动指针在度盘上指示出温度数值。双金属温度计结构简单,制造成本低,性能稳定耐振动,读数方便,如安装电接点装置还可以对温度进行现场控制,在能源化工、医药食品、轻工纺织、航空航海等行业部门得到了广泛应用。据统计,仅一套石油常压蒸馏装置,使用的双金属温度计就有数千支。双金属温度计按使用功能可分为指示型和带电接点型,按外形可分为角型(轴向型)、直型(径向型)、钝角型和可调角型。
2021年,市场监管总局发布了JJF1908-2021《双金属温度计校准规范》[1],并于2022年实施,代替JJG226-2001《双金属温度计》检定规程。新的校准规范对校准标准器进行了更新,对恒温设备的技术要求发生了变化,因此有必要对双金属温度计的测量不确定度进行重新评定。文中按照JJF 1059.1-2012《测量不确定度评定与表示》[2]的要求,对双金属温度计示值的不确定度分量进行分析,对典型测量不确定度进行评定,并提出提高测量准确度的方法。
1不确定度评定
1.1测量方法
双金属温度计的测量范围一般为-80℃~600℃,其校准采用比较法,即将标准水銀温度计(测量范围-60℃~300℃)或标准铂电阻温度计(测量范围-196℃~630.74℃)与被校双金属温度计同时置于恒温槽中,比较二者在同一温度点的差值。双金属温度计的量值溯源体系如图2所示。
在本例中,被校双金属温度计测量范围为0℃~100℃,表盘分度值2℃;校准用的标准水银温度计测量范围为50℃~100℃,校准点为100℃,标准水银温度计示值为99.92℃(分度值0.1℃,估读至0.01℃),其修正值+0.04℃;由于校准点为被校双金属温度计的示值上限,因此只进行正行程(升温)的校准,校准结果(双金属温度计的示值)为99.8℃(分度值2℃,估读至0.2℃);恒温槽采用恒温油槽,温度范围95℃~300℃。
1.2测量模型
双金属温度计在校准点的示值误差可以用式(1)表示:
Δt=t0-(ts+A)=99.8-(99.92+0.04)=-0.16℃ (1)
式(1)中,Δt为双金属温度计在100℃的示值误差,t0为双金属温度计示值,ts为标准水银温度计示值,A为标准水银温度计在100℃的修正值,单位均为℃。
1.3不确定度分量
1.3.1不确定度分量的A类评定
1.3.1.1标准水银温度计读数引入的不确定度
标准水银温度计的读数应估读至其分度值的1/10,即0.01℃,区间半宽为0.005℃,为均匀分布。标准水银温度计读数引入的不确定度分量为:
1.3.1.2被校双金属温度计的示值估读引入的标准不确定度
双金属温度计的示值估读到其分度值的1/10,即为0.2℃,区间半宽0.1℃,为均匀分布。则示值估读引入的标准不确定度为:
1.3.1.3被校双金属温度计测量重复性引入的
标准不确定度
对被校双金属温度计连续进行10次重复测量,结果如表1所示。
测量重复性引入的不确定度以单次测量的标准差表示:
对于示值估读引入的不确定度分量和测量重复性引入的不确定度分量,取二者中较大的,即:
u3=s=0.16℃(5)
1.3.2不确定度分量的B类评定
1.3.2.1标准水银温度计修正值引入的不确定度
根据标准水银温度计的不确定度评定报告,100℃时标准水银温度计示值修正值的扩展不确定度为=0.03℃,=2,则示值修正引入的不确定度分量为:
u4=0.03/2=0.015℃(6)
1.3.2.2标准水银温度计在检定周期内不做
零位修正引入的不确定度
水银温度计的玻璃外壳在升温和降温过程中,由于热胀冷缩和内部应力不均匀造成的影响,贮液泡的体积会发生变化,使得水银温度计的零位发生变化[3]。经检定合格的标准水银温度计,其在检定周期内零位的变化量不超过0.06℃,为均匀分布。其引入的不确定度分量为:
1.3.2.3恒温槽波动性引入的不确定度
按照双金属温度计校准规范的要求,选用的恒温油槽温度波动性不超过0.10℃/10min,区间半宽为0.05℃,为均匀分布。其引入的不确定度分量为:
1.3.2.4恒温槽温度均匀性引入的不确定度
恒温油槽的温度均匀性不超过0.20℃,区间半宽为0.10℃,为均匀分布。其引入的不确定度分量为:
1.4合成不确定度
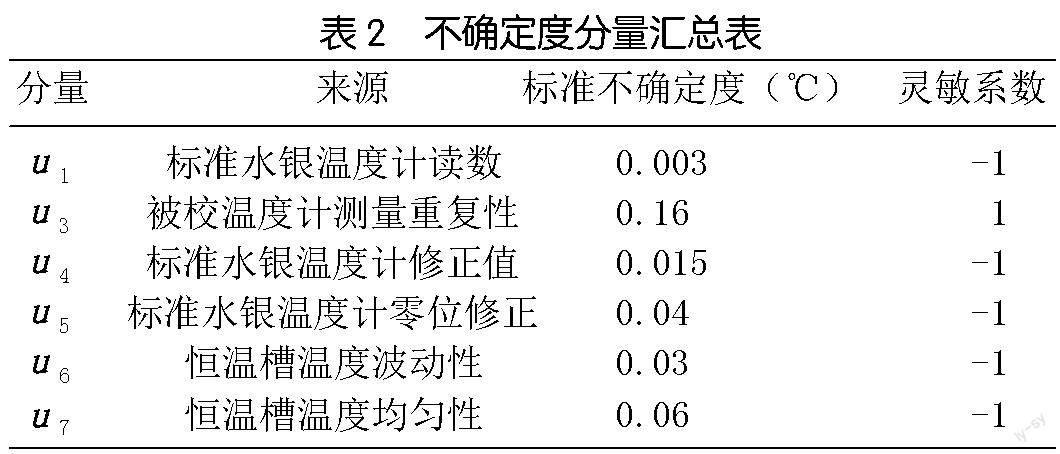
以上标准不确定度分量汇总见表2。
表中各不确定度分量互不相关,可采用方和根法合成,则有:
2测量结果不确定度表示和验证
2.1扩展不确定度
双金属温度计的测量不确定度可以用扩展不确定度表示,取=2,则有:
U=k·uc=2×0.18=0.4℃(11)
2.2测量结果的表示和测量不确定度的验证
以上测量结果可以表示为:被校双金属温度计在100℃的示值误差为-0.16℃,测量结果的扩展不确定度为0.4℃,扩展因子为2。
按照校准规范的要求,对5支2.0级的双金属温度计使用同一标准水银温度计在同一恒温槽中校准,根据JJF1094-2002《测量仪器特性评定》[4]的要求,示值误差的扩展不确定度应小于其最大允许误差绝对值的1/3,当被评定测量仪器的示值误差t的绝对值小于等于其最大允许误差的绝对值MPEV与示值误差的扩展不确定度之差时可判为合格,即:
丨Δt丨≤MPEV-U(12)
结果如表3所示。
可以看出,示值误差的扩展不确定度符合规范要求,说明不确定度评定过程合理。被校双金属温度计的示值误差均满足式(12),可以判定为合格。
3結语
对双金属温度计示值误差评定过程中的不确定度分量进行分析,可以看出,对其测量不确定度贡献较大的分量是被校双金属温度计测量重复性引入的不确定度。双金属温度计一般作为在线测量仪表安装在生产现场,因此不能通过增加测量次数的方式减小测量重复性,而应采用对多支温度计进行测量合并样本标准差的方式来进行[5]。
在使用双金属温度计时,其插入被测介质的深度应大于敏感元件的长度,对于插入长度小于300mm的双金属温度计,其插入深度应大于70mm,插入长度大于300mm的双金属温度计,其插入深度应大于100mm[6]。读取双金属温度计示值时应轻敲温度计外壳,以避免指针卡顿;双金属温度计在安装使用维修过程中,应避免使保护管弯曲变形;部分双金属温度计含有铁磁材料,在强磁场中工作时会产生较大测量误差,甚至发生不可逆改变,应尽量避免。
参考文献
[1]全国温度计量技术委员会.双金属温度计校准规范:JJF 1908-2021[S].北京:2021.
[2]全国法制计量管理计量技术委员会.测量不确定度评定与表示:JJF 1059.1-2012[S].北京:2012.
[3]金志军,刘薇,陈伟昕,曾永春,张军.标准水银温度计替代研究现状与发展分析[J].工业计量,2021,31(05):50-51.DOI:10.13228/j.boyuan.issn1002-1183.2021.0042.
[4]全国法制计量管理计量技术委员会.测量仪器特性评定:JJF 1094-2002[S].北京:2002.
[5]吴建英.温度计量 [M].北京,中国标准出版社:2021.
[6]于秀甲.双金属温度计检定方法及注意事项[J].石化技术,2018,25(09):265.

