城市群圈层结构下的协同创新与产业升级

陈丛波 叶阿忠 林壮

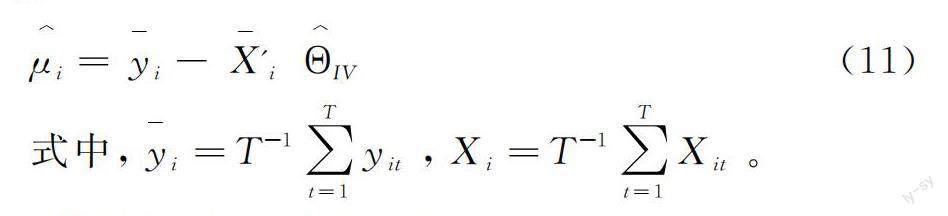
摘 要：采用2009—2019年长三角城市群面板数据，构建半参数二机制动态空间杜宾模型考察协同创新对产业升级的动态空间效应及其城市异质性。研究发现，长三角城市群产业升级具有显著动态性和空间相关性，邻近城市协同创新对产业升级的动态空间效应不可忽视；中心城市与外围城市产学合作专利均能在短期和长期推动邻近城市产业升级，但中心城市对协同创新的政府资助在长期内不利于外围城市产业升级；协同创新对本地城市产业升级的当期作用呈现边际递减趋势，维持中心城市产业升级优势更多需要来自邻近城市协同创新对中心城市的空间溢出，而不是中心城市自身协同创新优势。研究结果有助于全面认识协同创新对产业升级的动态空间效应，对推动圈层结构下的中心城市与外围城市创新一体化发展，进而实现城市群整体产业升级具有现实意义。

关键词：圈层结构；协同创新；产业升级；半参数二机制动态空间杜宾模型

DOI：10.6049/kjjbydc.2022100547

中图分类号：F290

文献标识码：A

文章编号：1001-7348（2023）11-0092-09

0 引言

中共二十大报告明确提出，建设现代化产业体系，坚持把发展经济的着力点放在实体经济上，推进新型工业化。创新是第一动力，当前中国迫切需要通过创新驱动产业升级实现经济增长动能转换，在全球竞争中脱颖而出，引领新一轮产业变革。中国产业升级涉及的人口最多、产业结构最完整，但呈现出显著的空间非均衡性，外围城市产业结构薄弱、城市内部创新主体协同能力不足，限制了协同创新对产业升级的驱动作用。伴随高铁等基础设施建设，空间知识溢出成为产业升级的催化剂（毛琦梁， 2019），外围城市与中心城市产业升级的非均衡性可以通过空间知识溢出得到弥补。因此，有必要研究圈层结构下协同创新对产业升级的空间溢出效应。

已有研究表明，技术创新^[1-2]和协同创新^[3]的空间溢出效应是地区产业升级的重要驱动因素。然而，城市群由多中心的异质城市组成^[4]，中心城市和外围城市通常具有圈层结构，对于圈层结构下协同创新空间溢出如何作用于邻近城市产业升级，现有研究并未给予过多关注。圈层结构的特点在于中心城市和外围城市既具有密切联系，又存在较大发展差距。一方面，圈層结构下的中心城市与外围城市产业联系紧密，产业升级和技术进步方向具有高度一致性，协同创新对产业升级的空间效应可能更加显著；另一方面，中心城市与外围城市的协同创新、产业升级水平存在明显差距，可能会阻碍协同创新对邻近城市产业升级的空间溢出效应。目前尚无文献研究城市群圈层结构下协同创新对产业升级的空间溢出效应。那么，中心城市协同创新空间溢出是否会对外围城市产业升级产生积极影响？外围城市协同创新能否反作用于中心城市，为中心城市产业升级提供备选技术路径？如何有效利用城市群一体化发展机遇，针对性制定城市群创新发展战略，推动城市群产业升级？

为回答上述问题，本文选择长三角城市群地级及以上城市为研究对象，分析中心城市和外围城市协同创新对产业升级动态空间效应的作用途径。然后，结合高铁通行数据与城市吸引力模型构建空间权重矩阵和半参数二机制动态空间杜宾模型，实证检验协同创新对产业升级的动态空间溢出效应及其城市异质性，并借助半参数技术检验协同创新对本地产业升级的非线性影响。最后，形成结论和政策启示。

1 文献综述

归纳和总结现有文献发现，学者们对创新或协同创新驱动本地产业升级，以及空间溢出驱动邻近地区产业升级进行了大量研究。

在创新驱动本地产业升级方面，已有研究主要聚焦创新对产业升级的驱动作用。学界普遍认为，创新是产业升级的驱动力^[5]。但是，并非所有创新都能驱动产业升级，中间还存在一个技术选择问题^[6]。只有当通过自主创新和学习活动选择的技术进步方向与区域条件相一致时，才能有效促进区域产业升级和经济发展^[7]；反之，当技术进步方向与区域条件不一致时，就会出现创新成果产出增加却难以引致产业升级的悖论^[8]。究其原因，我国高校和企业创新侧重方向分歧明显，高校对企业技术创新支持力度不够^[9]，导致技术进步方向出现偏差和创新的经济效应未能完全发挥。目前，关于协同创新驱动产业升级的研究相对缺乏。相比于其它类型的创新，协同创新将异质性创新主体组织为具有共同目标和价值观的创新共同体（王峥，龚秩， 2018），与产业升级匹配程度更高。孙大明和原毅军^[3]发现协同创新通过降低创新成本、提高劳动生产率、技术溢出效应和改造传统产业等途径推动本地产业升级。

在空间溢出驱动邻近地区产业升级方面，已有研究主要关注产业转移和空间知识溢出对产业升级的影响。有学者用“雁阵模式”解释我国发达地区向欠发达地区的产业转移，如张其仔^[10]认为我国东部地区将淘汰产业向中西部地区转移，地区间产业升级形成“雁阵模式”。也有学者对“雁阵模式”持批判态度，如李雯轩和李晓华^[11]认为中西部地区通过承接东部地区产业转移实现产业升级面临诸多困境。对于空间知识溢出驱动产业升级，金浩和刘肖^[12]认为产业协同集聚有利于知识溢出，并通过技术创新推动经济增长；纪玉俊和李超（2015）构建空间误差模型对我国省级数据进行实证研究，发现地区创新对产业升级的作用存在空间知识溢出效应；毛琦梁（2019）基于地级市的实证研究发现，空间知识溢出能够促进地区产业升级。考虑城市异质性和非线性作用后，李洪涛和王丽丽^[13]发现中心城市科技创新对城市群整体产业高级化和多样化具有先抑制后促进的U型作用；孙大明等^[3]基于省际层面数据检验协同创新对产业升级的空间溢出效应。

已有成果为本文研究奠定了良好基础，但仍存在可改进之处：一是未能深入分析不同类型城市协同创新对产业升级的空间溢出效应差异，特别是中心城市与外围城市协同创新对产业升级的异质性空间溢出效应尚待发现；二是未考虑协同创新空间溢出效应对产业升级的动态影响；三是实证方法多采用线性空间模型，若放松空间依赖关系的线性假设，可能使模型设定更符合实际，得到更准确的估计结果。为此，本文研究城市群圈层结构背景下，中心城市和外围城市协同创新对产业升级的动态空间溢出效应及其异质性，分析中心城市产业升级在圈层结构中处于优势地位的原因。在实证上，首次应用半参数动态门限空间杜宾模型检验中心城市和外围城市协同创新对产业升级的异质性空间溢出效应。

2 理论分析与研究假设

中心城市和外围城市是城市群系统圈层经济结构的两个组成部分，二者存在密切的空间联系。中心城市和外围城市协同创新对产业升级的动态空间溢出效应可以归纳为以下方面：

首先，中心城市协同创新通过空间知识溢出提高外围城市创新能力，为外围城市产业升级提供潜在技术机会窗口。中心城市具有创新资源集聚优势，外围城市通过从中心城市获得空间知识溢出，摆脱本地资源禀赋不足、创新人才集聚规模偏小、高端研发人员缺乏等创新困境，提高创新能力。圈层结构的外围城市更容易学习、模仿中心城市的先进技术，因而圈层结构的城市间空间知识溢出效应更加显著。近年来，以高铁为代表的运输基础设施逐渐完善，城市群一体化程度得以提高，有利于非中心城市获取空间知识溢出，提升自身创新能力^[14]。在地理邻近、文化邻近和技术邻近等多维度邻近影响下，空间知识溢出对邻近地区的产业升级起到正向作用（毛琦梁， 2019）。圈层结构下中心城市与外围城市的多维度邻近程度更高，使得中心城市协同创新成果容易与外围城市产业升级技术方向匹配，中心城市空间知识溢出对外围城市产业升级的作用更显著。基于此，本文提出以下假设：

H₁：城市群圈层结构下，中心城市协同创新通过空间知识溢出在短期内促进外围城市产业升级。

其次，中心城市协同创新推动本地产业趋向成熟，进而加速成熟产业向外围城市转移，带动外围城市产业升级。根据产业升级的生命周期理论，处于不同生命周期的产业从不同类型城市集聚中获得知识溢出^[15-16]。中心城市协同创新能够促进本地多样化知识溢出，新兴产业通过与外部创新主体协同创新突破产业发展的技术瓶颈，提高创新效率。产业进入成熟期后，导致低生产效率的主因由技术瓶颈转变为生产规模偏小，此时，中心城市多样化知识溢出对产业升级的重要性下降。受中心城市相对较高的拥挤成本影响，成熟产业被迫迁出中心城市，成熟产业迁出中心城市后，更倾向于向圈层结构的外围城市迁入，理由如下：

一是历史惯性说。企业选址决策会受到往期决策的影响，城市群圈层结构的形成具有历史积淀，中心城市对外围城市的辐射力长期以“圈”的形式扩散^[17]，形成产业迁移的历史惯性。中心城市产业向外围城市迁移的历史经验给当前产业选址决策提供了更多信息参考。在没有出现明显变动因素的情形下，决策者更倾向于“照旧”，以使决策更具确定性。二是多维度邻近说。Boschma^[18]以多维度邻近作为理论工具解释空间知识溢出。该理论工具也可用于揭示圈层结构下外围城市承接成熟产业的特殊优势。圈层结构的地理特征和历史演化特征使中心城市与外围城市形成紧密的地理邻近、制度邻近、文化邻近及技术邻近，从而降低信息交流和要素流动成本，为产业转移创造有利环境。三是政策导向说。地方政府在产业转移中扮演重要角色^[19]，产业迁出地和迁入地政府对共同利益达成高度认同是产业转移的基础。圈层结构下的中心城市与外围城市政府之间互信度高，容易在博弈中达成一致。组成圈层结构的城市常常处于同一个省级区域，上级政府更乐意产业在省内城市间转移，带动全省产业升级。考虑到协同创新促进本地产业成熟和产业转移具有时间滞后，本文提出如下假设：

H₂：城市群圈层结构下，中心城市协同创新通过产业迁移对外围城市产业升级存在长期推动作用。

上述分析回避了中心城市产业升级过程中的有限理性问题。更现实的假设是，中心城市和外围城市都不得不基于各自拥有的不完全知识，尽力构造和强化产业升级路径。从中心城市视角看，其在上一轮技术革命中构造了更优的产业升级路径，并在累积循环作用下形成知识元素多样化优势，使其在下一轮技术革命中有更大机会创造产业升级路径。然而，根据有限理性假设，即使是中心城市，其知识多样性和知识重组机会也是有限的，產业升级路径无法达到最优。因此，中心城市需要从外部城市获得知识元素和知识重组机会，使产业升级路径更接近最优。本文认为，圈层结构下外围城市与中心城市的知识元素构成具有异质性，同时二者的产业之间存在技术关联性。这种异质性和技术关联性使得外围城市与中心城市的认知距离不太远也不太近。太远的认知距离会增加知识吸收难度，太近的认知距离则不利于创新成果产生^[18]。因此，外围城市协同创新能够帮助中心城市在短期内获得产业升级所需的特定知识元素，也能在长期内不断通过重组知识元素创造产业升级的可能路径。基于此，本文提出如下假设：

H_3a：在产业升级的动态过程中，外围城市协同创新能够在短期内推动中心城市产业升级；

H_3b：在产业升级的动态过程中，外围城市协同创新能够在长期内推动中心城市产业升级。

3 实证研究设计

3.1 实证模型构建

协同创新对城市产业升级的影响具有空间性和动态性，即前期协同创新会促进当期本地城市和邻近城市的产业升级。同时，城市产业升级是一个动态过程，前期产业升级对当期产业升级施加惯性影响。因此，仅考虑协同创新等驱动因素的当期影响不符合产业升级的实际情况，需要在实证模型中引入被解释变量、解释变量和空间滞后项的时间滞后作为被解释变量，构建动态空间杜宾模型作为本文基准模型。

式中，Sop_it代表城市i第t年的产业升级水平；Coi_it代表城市i第t年的协同创新水平，包括校企协同创新成果Comp_it和政府研发资金资助Gov_it两个子变量；X_it代表控制变量向量。以被解释变量和协同创新的空间滞后项Sop^*_it=∑Nj=1W_ijSop_jt和Coi^*_it=∑Nj=1W_ijCoi_jt反映当期空间溢出对产业升级的影响， W_ij为空间权重矩阵第i行第j列的元素；用变量的时间滞后Sop_it－1和X_it－1衡量动态效应；采用空间滞后项的时间滞后Sop^*_i，t－1=∑Nj=1W_ijSop_j，t－1和Coi^*_i，t－1=∑Nj=1W_ijCoi_j，t－1反映动态空间效应；μ_i、ε_it分别是个体固定效应和随机误差项。

考虑到空间溢出来自城市间的经济互动，借鉴李治等^[20-21]构建的修正引力模型，以城市间经济联系紧密程度与施加引力城市对外辐射强度的比值作为空间权重矩阵元素W_ij，反映城市间经济互动的强弱。空间权重矩阵元素W_ij的计算公式为：

式中，CP_ij表示施加引力城市i与接受引力城市j的经济联系紧密程度，C_i表示施加引力城市i的对外施加引力总强度。CP_ij计算公式为：

式中，Y_i、Y_j分别表示城市i、j的地区生产总值，Y_iY_j表示两个城市地区生产总值的乘积，D_ij表示城市间的实际交通距离。随着高铁的普及，高铁成为城际运输的最主要方式，因而以城市i到城市j的高铁最短到达时间衡量实际交通距离。C_i计算公式为：

式中，r_i为城市i的城市半径，r²_i=S_i/π，S_i为城市i的行政区划面积。需要指出的是，由于式（2）中的分母与城市i相关，本文构建的空间权重矩阵是非对称的，即W_ij≠W_ji。

刻画圈层结构下城际关系的难点在于区分中心城市与外围城市之间的空间溢出，而模型（1）为经典动态空间杜宾模型，仅考察线性空间依赖关系。为验证本文理论假设，还需要区分城市群圈层结构下中心城市和外围城市产业升级受到邻近城市协同创新的异质性影响。为此，本文借鉴二机制空间计量模型构建方法^[22]，在模型（1）中协同创新空间滞后项后引入虚拟变量D_it和D-_it，构建二机制动态空间杜賓模型。

式中，若城市i为中心城市，则D_it=1；若城市i为外围城市，则D_it=0，D-_it=1－D_it。虚拟变量D_it和D-_it的引入使线性动态空间杜宾模型转变为二机制动态空间杜宾模型，γ₁、φ₁和γ₂、φ₂分别表示中心城市和外围城市产业升级对邻近城市协同创新空间溢出及动态空间溢出的反应系数。

协同创新具有多种创新主体，因而其对产业升级的作用比其它创新更为复杂，这可能使协同创新与产业升级之间呈现非线性关系。因此，本文在模型（5）基础上引入协同创新作为非参变量，构建半参数二机制动态空间杜宾模型。

式中，g（·）为未知函数，通过引入非参项gCoi_it，避免预设协同创新与产业升级间表现为线性关系可能引起的误差。模型（6）可通过偏导数图形式刻画协同创新与产业升级间的非线性关系，并且在二者存在非线性关系的情形下，参数部分可以得到更准确的估计。

3.2 模型估计方法

根据学者提出的门限动态空间模型估计方法^[23]，本文在二机制动态空间杜宾模型基础上进一步引入非参项，构建半参数二机制动态空间杜宾模型。非参项的引入导致模型估计难度大大提高，本文给出一般形式的半参数二机制动态空间杜宾模型及其估计方法，模型一般形式设定为：

式中，y_it是被解释变量，S_it=S_1it，…，S_dSit'为解释变量，将机制划分引入解释变量S_it的空间滞后项S^*_it及其时间滞后项S^*_i，t－1；非参变量使用更一般的P_it表示，P_it=P_1it，…，P_dPit'。若gP_it≠0，则可将其归入固定效应项，因此，假设gP_it=0。式（7）可改写为：

式中，X'_itΘ是模型的参数估计部分，解释变量X'_it=（y_it－1，y^*_it，y^*_i，t－1，S_itD_it，S^*_itD_it，S^*_i，t－1D_it，S_itD-_it，S^*_itD-_it，S^*_i，t－1D-_it）为内生变量，参数分量Θ=α，ρ，λ，δ₁，γ₁，φ₁，δ₂，γ₂，φ₂'，S_1t，P_1t，y_1t，…，S_Nt，P_Nt，y_Nt是在R^d_S+d_P+1上取值的随机变量向量序列；解释变量X_it为内生变量，与误差项相关。

设H_1t，…，H_Nt是在R^6d_S+3上与y^*_it相关的随机变量向量，且EH_itμ_it=0，EH_itμ_it|X_it，P_it=0，称H_it为工具变量向量。参考半参数动态空间杜宾模型估计方法，参数分量Θ的工具变量估计为：

式中，H_#it=H_1it，…，H_6dS+3，it'是工具变量向量，m︿₁（p）、m︿₂（p）分别是m₁（p）=EX_it|P_it=p和m₂（p）=Ey_it|P_it=p的局部线性估计。得到参数分量的工具变量估计后，非参数分量的工具变量估计为：

得到参数部分和非参数部分的具体参数值后，基于修正的最小二乘思想，个体固定效应μ_i的估计表达式为：

3.3 数据来源与变量说明

中国正在实施的长三角一体化发展战略涵盖江、浙、沪、皖的41个地级及以上城市，其中，上海、南京、杭州、合肥等中心城市拥有众多国内一流大学和研究所，产业升级水平也居于全国前列。长三角城市群拥有大量与中心城市经济联系紧密的外围城市，区域内的上海都市圈、南京都市圈、合肥都市圈、杭州都市圈等都表现出显著的圈层经济结构特征。长三角城市群是我国三大经济增长极之一，本文研究对其它具有圈层结构的城市群发展也具有借鉴意义。基于《中国城市统计年鉴》和国家知识产权局专利数据库检索数据，收集2009—2019年长三角地区地级及以上城市面板数据。

3.3.1 被解释变量

城市产业升级水平是本文被解释变量。学界对产业升级的研究包含两方面内容：一是产业结构升级，主要关注要素投入和产品产值在各产业间分布的变动；二是价值链升级，聚焦产出水平与要素投入量之间比例的提高。產业结构比例变迁本身并无高级化的空间，仅指劳动力由低生产率产业流向高生产率产业，引起人均产值提高。价值链升级以产业结构比例固定为前提，认为各产业处于交互供求的关联机制下，一个产业的扩张必须以其它关联产业同比例扩张为条件^[24]。然而，固化城市产业结构比例的前提假设与现实存在很大分歧，中国正在发生大规模产业区域转移现象，一大批城市产业结构比例处于变化状态。本文认为，衡量城市产业升级应包括产业结构比例变迁和要素—产出比例提高两部分内容，以城市各产业产值比重表征产业结构比例变迁，以劳动生产率表征要素—产出比例提高，使用二者的乘积表征城市产业升级水平。

式中，Y_kit表示第t年城市i产业k的产值，Y_it表示第t年城市i的地区总产值；LP_kit表示第t年城市i产业k的劳动生产率，用产业k的产值除以就业人数衡量。

3.3.2 核心解释变量

城市协同创新水平是本文核心解释变量。协同创新涉及企业、高校、政府等异质性创新主体，协同创新按合作对象可分为直接主体与间接主体间的协同创新、直接主体间的协同创新。协同创新合作表现为协同创新产出和协同创新投入两种形式。其中，协同创新产出主要是指各参与方共同的创新成果，本文使用协同创新成果近似表征城市协同创新水平。借鉴夏丽娟等（2017）的做法，使用高校和企业合作申请发明专利数（CoP_it）衡量直接主体间的产学创新合作成果。相对于实用新型专利和外观设计专利，发明专利技术含量更高，更能代表协同创新研发成果。本文数据来自国家知识产权局专利检索数据库，数据检索方式为将申请日设定为样本期内某一年份，在申请人地址栏输入城市名，在专利申请人检索栏输入大学、学院和公司、集团、企业、厂的两两组合。

协同创新投入包括人员、资金等创新要素投入，高校与企业、政府间的人员流动主要通过高校师生参与项目、学术创业的形式进行。由于高校学生在高校与企业、政府间流动是临时的，高校教师一般同时属于高校和企业，高校学生和教师的流动性较差，人员流动对协同创新的影响较小。政府通常不直接参与创新，是协同创新的重要间接主体，白俊红和蒋伏心^[25]使用政府对城市研发机构和企业的资金资助衡量间接主体与直接主体间的协同创新。考虑到政府资金资助与城市研发机构及企业数量相关，仅用政府资金资助金额不能准确衡量政府支持协同创新的强度，本文以政府资金资助除以研发机构和企业的几何平均数估算政府资金资助的协同创新，计算公式为：

式中，Fund为政府科学技术支出，N_Uni、N_com分别为高等学校数和规模以上工业企业数，使用几何平均数可以避免N_Uni和N_com差距过大，导致高等学校被忽视。

3.3.3 控制变量

本文选择信息化水平、外商投资水平和基础设施水平为控制变量。其中，信息化水平（pinter）采用每万人宽带互联网用户数表征，外商投资水平（pfdi）采用外商直接投资占城市经济产值的比重表征，基础设施水平（proad）采用城市道路人均面积表征。

4 实证分析

4.1 线性动态空间杜宾模型估计结果

考虑到协同创新的两个表征变量合作发明专利数量与政府对高校、企业研发资金投入可能存在相关关系，干扰最终估计结果，本文首先分别将两个变量及其时间滞后项、空间滞后项分别带入线性动态空间杜宾模型，再将两个变量同时带入模型，对比实证结果，以检验稳健性。表1给出了3个线性动态空间杜宾模型的估计结果。

被解释变量时间滞后项Sop_it－1的回归系数在3个线性动态空间杜宾模型中均显著为正，说明城市产业升级过程在时间维度上具有累积循环作用，往期产业升级对当期产业升级具有积极影响。历史上，圈层结构的中心城市始终占据产业升级的“头雁”位置，部分原因就在于产业升级的累积循环过程使前期取得产业升级成功的中心城市更容易在当期延续产业升级的惯性。被解释变量的空间滞后项WSop_it及其时间滞后项WSop_it－1的回归系数均显著为正，说明长三角城市群产业升级具有显著的空间相关性，某一城市的产业升级水平会受到其它城市当期和往期产业升级水平的影响。城市间密切的经济联系是圈层结构的主要特征，因此本文在圈层结构下分析协同创新与产业升级的空间关系具有一定合理性。

产学创新合作专利CoP_it的回归系数在模型1和模型3中均不显著，但其时间滞后项CoP_it－1的回归系数显著为正，说明协同创新专利成果转化为产业升级动力需要时间。相比之下，其空间滞后项WCoP_it的回归系数显著为正，说明协同创新专利成果能在当期促进邻近城市产业升级。原因在于，圈层结构城市间紧密的联系为创新成果空间溢出提供了高效扩散渠道，使外部城市的协同创新成果对本地产业升级起到“他山之石，可以攻玉”的效果。相近实证研究中，孙大明和原毅军^[3]以企业协同创新资本存量作为核心解释变量，构建静态空间杜宾模型，发现省际层面协同创新空间滞后项的回归系数显著为正，可与本文结果相互印证。本文进一步引入WCoP_it的时间滞后项WCoP_it－1，其回归系数依然显著为正，说明外部城市协同创新的产业升级效应存在时间上的延续性。

政府资助协同创新Gov_it的回归系数在模型2和模型3中为负，而其时间滞后项Gov_it－1的回归系数却显著为正。造成政府资助当期值回归系数为负的原因可能来自其对金融机构资助协同创新的挤出作用。金融机构更倾向于资助见效快的协同创新项目，而政府资助更关注创意，对协同创新过程更有耐心，因此，短期内政府资助协同创新反而不利于产业升级。然而，滞后一期的回归系数显著为正，说明经过一段时间磨合后，高校和企业能够有效利用政府资助资源进行联合研发，获得更具突破性的协同创新成果，形成对产业升级的推动力。相近研究中，白俊红和蒋伏心^[25]实证研究发现，政府资助对区域创新绩效的当期影响为负或显著性水平较低，而滞后一期的回归系数显著为正，且数值更大。值得注意的是，空间滞后项WGov_it的回归系数显著为正，其时间滞后项WGov_it－1的回归系数显著为负。主要原因可能是长期作用下，政府资助会对周围城市产生虹吸效应，促使周围城市的协同创新资源向中心城市集聚。后文二机制动态空间杜宾模型中，中心城市和外围城市空间滞后项的时间滞后系数正负差异也说明中心城市政府资助存在对外围城市的虹吸效应。

控制变量中，外商投资及其时间滞后项与产业升级表现出正相关关系。信息和交通基础设施当期值的回归系数为负，其时间滞后项与产业升级表现出正相关关系，这可能是因为基础设施建设占用了同期用于产业升级的资金，导致短期内基础设施建设不利于产业升级，对产业升级的正向作用需要经过一段时间的累积才能逐渐发挥出来。

4.2 协同创新对产业升级动态空间效应的城市异质性分析

为描述圈层结构下协同创新对中心城市和外围城市产业升级的异质性空间溢出效应，本文进一步将线性动态空间杜宾模型扩展为二机制动态空间杜宾模型。将协同创新的两个表征变量代入式（5）进行估计，模型4使用产学合作专利衡量协同创新，模型5使用政府资助衡量协同创新，结果如表2所示。本文重点关注协同创新对产业升级空间溢出效应的动态性和异质性影响，因而表2只列出了核心解释变量的空间滞后项及其时间滞后项在不同机制中的回归系数，D_it代表中心城市，D-_it代表外围城市。

模型4和模型5中，对于产学合作专利衡量的协同创新，中心城市与外围城市空间滞后项的回归系数分别为0.523和0.314，回归结果显著为正；对于政府资助衡量的协同创新，中心城市与外围城市空间滞后项的回归系数分别为1.660和1.060，回归结果在1%的水平下显著为正。由此可知，中心城市和外围城市都能够从邻近城市协同创新成果中获得产业升级的正向空间溢出，促进城市产业升级。该结果验证了H₁，即中心城市协同创新通过空间知识溢出促进当期外围城市的产业升级。同时，外围城市能够对当期中心城市的产业升级产生正向影响，即H_3a关于外围城市协同创新在短期内促进中心城市产业升级的判断符合现实。无论是产学合作专利还是政府资助，中心城市的回归系数均显著大于外围城市的回归系数，表明中心城市能够更为敏锐地察觉到邻近城市协同创新成果，更容易從中获取产业升级的驱动力。本文认为，圈层结构的中心城市之所以长期保持产业升级的“头雁”地位，不完全是因为城市内部的累积循环效应，中心城市获取空间溢出的长期优势也是导致圈层结构下城市产业升级水平始终存在差距的重要原因。

表2结果显示，中心城市产学合作专利与政府资助空间滞后项的时间滞后回归系数分别为0.431和0.602，均显著为正，说明外围城市协同创新对中心城市产业升级具有长期促进作用，H_3b得到验证。外围城市产学合作专利空间滞后项的时间滞后回归系数为0.142，在5%的水平下显著为正，说明中心城市协同创新成果能够长期推动外围城市产业升级，H₂得到验证。政府资助空间滞后项的时间滞后回归系数为-0.335，在5%的水平下显著，不符合H₂的判断，可能是因为中心城市的政府资助对外围城市产生虹吸效应，导致外围城市创新资源不断向中心城市集聚，不利于外围城市产业升级。

4.3 进一步讨论：本地协同创新还是空间溢出

由线性动态空间杜宾模型和二机制动态空间杜宾模型回归结果可知，本地城市产学合作专利当期值CoP_it对产业升级的回归系数均不显著，原因在于创新成果转化为产业升级驱动力需要过程和时间。为验证该解释是否可靠，本文将当期产学合作专利CoP_it作为非参项引入式（6），构建半参数二机制动态空间杜宾模型。图1报告了协同创新对产业升级的边际影响随协同创新变化的趋势，横轴为城市产学合作专利当期值，纵轴表示产学合作专利对本地产业升级的偏导数。偏导数整体趋势呈现出非常明显的非线性特征，当期协同创新成果越丰富，对本地产业升级的边际驱动作用反而越小。产业吸收效率越高，越能快速将新技术转化为新产品和新生产工艺。当产业对创新成果的吸收效率不足以快速将新技术转换为升级动力时，就会出现图1中协同创新成果丰富却对当期产业升级边际驱动作用不强的情况，需要延长对创新成果的吸收时间。也就是说，在吸收效率有限的情形下，协同创新成果越丰富，其对产业升级的促进作用就越滞后。

一般认为，中心城市的本地协同创新优势有助于维持其产业升级优势。然而，本文将图1中当期协同创新的回归系数与协同创新空间滞后项的回归系数进行对比却得到相反观点。圈层结构中，中心城市拥有更高的协同创新水平，但偏导图显示本地高水平协同创新在当期对产业升级的驱动作用较弱，说明中心城市产业升级的主要驱动力不是来自本地协同创新。对比协同创新空间滞后项在中心城市机制下的回归系数发现，中心城市产业升级的主要驱动力来自协同创新的空间溢出效应。这一发现的意义在于，考察城市产业升级分异的形成原因时，不仅要考虑产业升级推动因素的空间分布，更要考虑异质城市的空间溢出效应。

5 结论与政策启示

基于2009—2019年长三角城市群41个城市面板数据，构建非对称空间权重矩阵和半参数二机制动态空间杜宾模型，考察圈层结构下中心城市和外围城市协同创新对产业升级的异质性动态空间溢出效应，得到如下结论：首先，线性动态空间杜宾模型计量结果显示，长三角城市群产业升级具有显著动态性和空间相关性，往期产业升级水平和邻近城市产业升级水平对城市产业升级具有正向影响；邻近城市产学合作专利对本地产业升级存在长期正向空间溢出效应；政府资助协同创新短期内有利于邻近城市产业升级，但从长期看，由于存在虹吸效应，不利于邻近城市产业升级。上述结果表明，圈层结构下城市间协同创新的动态空间溢出效应对产业升级起到不可忽视的作用。其次，二机制动态空间杜宾模型计量结果显示，产学合作专利的动态空间溢出效应对中心城市和外围城市产业升级具有积极影响，表明无论在短期还是长期内，中心城市和外围城市产学合作专利均能够推动邻近城市产业升级。政府资助协同创新的基本结论与产学合作专利相同，但由于存在虹吸效应，中心城市对协同创新的政府资助可能在长期内不利于外围城市产业升级。最后，绘制协同创新非参项对本地城市产业升级的偏导图发现，产学合作专利对本地城市当期产业升级的边际驱动作用呈现随合作专利数增加而减弱的非线性特征。同时，产学合作专利对产业升级的空间溢出效应大于中心城市产学合作专利对自身产业升级的边际效应，说明协同创新对产业升级的空间溢出效应是中心城市维持产业升级优势的重要原因。

当前，中国正在积极推进区域协调发展战略和创新驱动发展战略，创新一体化是推动城市群产业升级的重要发展途径之一。在此背景下，根据上述研究结果，提出如下政策建议：第一，出台创新激励政策应充分考虑城市产业升级路径的特殊性，不能仅追求创新成果和创新投入的数量增长，还要发挥协同创新对城市产业升级的驱动作用。通过搭建跨城市的高校—企业、政府—企业协同创新平台，推出相关跨城市合作激励政策，促进城市群内创新要素的充分流动和高效共享，是城市群协同创新驱动产业升级的有效治理方式。第二，着力推动以中心城市为核心、外围城市为支撑的创新一体化发展，发挥中心城市协同创新在产业升级中的“头雁”作用，同时兼顾外围城市协同创新，为城市群产业升级提供多样化发展路径。既要发挥圈层结构城市间联系密切的“合之利”，又要注重探索圈层结构城市创新的多样化路径，形成不同城市产业升级的“分之利”，为城市群产业升级提供持久的动力源泉。第三，中心城市和外围城市要利用圈层结构城市间联系紧密的优势，发挥产业升级的空间溢出效应。推动中心城市和外围城市的创新主体建立创新同盟，使不同城市的创新主体间形成相互关联、相互支持的创新网络，奠定城市群协同创新推动产业升级的组织基础。

参考文献：

[1] 周璇， 陶长琪. 水平式知识溢出、技术嵌入式创新与产业结构协调化——以我国制造业为例[J]. 科研管理， 2021，42（7）：126-136.

[2] 周璇， 陶长琪. 技术融合式创新对产业结构高度化的驱动效应研究——基于垂直式知识溢出视角[J]. 管理評论， 2021，33（7）：130-142.

[3] 孙大明， 原毅军. 空间外溢视角下的协同创新与区域产业升级[J]. 统计研究， 2019，36（10）：100-114.

[4] 胡序威. 应厘清与城镇化有关的各种地域空间概念[J]. 城市发展研究， 2014，21（11）：1-4.

[5] 周叔莲，王伟光. 科技创新与产业结构优化升级[J]. 管理世界， 2001，17（5）：70-78.

[6] 黄茂兴， 李军军. 技术选择、产业结构升级与经济增长[J]. 经济研究， 2009，44（7）：143-151.

[7] YI L. The dynamics of local upgrading in globalizing latecomer regions： a geographical analysis[J]. Regional Studies， 2017，51（6）：880-893.

[8] 阳立高， 龚世豪， 王铂， 等. 人力资本、技术进步与制造业升级[J]. 中国软科学， 2018，33（1）：138-148.

[9] 王文静， 高敏雪. 中国产学合作模式下的知识存量研究[J]. 数量经济技术经济研究， 2019，36（4）：139-154.

[10] 张其仔. 中国能否成功地实现雁阵式产业升级[J]. 中国工业经济， 2014，31（6）：18-30.

[11] 李雯轩， 李晓华. 新发展格局下区域间产业转移与升级的路径研究——对“雁阵模式”的再探讨[J]. 经济学家， 2021，33（6）：81-90.

[12] 金浩，刘肖.产业协同集聚、技术创新与经济增长——一个中介效应模型[J].科技进步与对策，2021，38（11）：46-53.

[13] 李洪涛， 王丽丽. 中心城市科技创新与城市群产业高级化及多样化[J]. 科研管理， 2022，43（1）：41-48.

[14] 王雨飛， 倪鹏飞， 赵佳涵， 等. 交通距离、通勤频率与企业创新——高铁开通后与中心城市空间关联视角[J]. 财贸经济， 2021，42（12）：150-165.

[15] DURANTON G， PUGA D. Nursery cities： urban diversity， process innovation， and the life cycle of products[J]. American Economic Review， 2001，91（5）：1454-1477.

[16] POTTER A， WATTS H. Evolutionary agglomeration theory： increasing returns， diminishing returnsm and the industry life cycle[J]. Journal of Economic Geography， 2011，3（11）：417-455.

[17] 张亚斌， 黄吉林， 曾铮. 城市群、“圈层”经济与产业结构升级——基于经济地理学理论视角的分析[J]. 中国工业经济， 2006，23（12）：45-52.

[18] BOSCHMA R A. Proximity and innovation： a critical assessment[J]. Regional Studies， 2005，39（1）：61-74.

[19] 黄志基， 朱晟君， 石涛. 工业用地出让、技术关联与产业进入动态[J]. 经济地理， 2022，42（5）：144-155.

[20] 李治， 连玉君， 李培， 等. “圈层”结构、时空差异与能源强度——以十大城市群为例[J]. 城市发展研究， 2015，22（1）：56-65.

[21] 李治， 郭菊娥， 李培. 中国城市群“圈层”结构对能源强度影响实证[J]. 中国人口·资源与环境， 2014，24（11）：26-32.

[22] ELHORST J P， FRERET S. Evidence of political yardstick competition in France using a two-regime spatial Durbin model with fixed effects[J]. Journal of Regional Science， 2009，49（5）：931-951.

[23] 韩晓祎， 蔡争争， 朱艳丽. 门槛空间动态面板模型的贝叶斯估计及其应用研究[J]. 数量经济技术经济研究， 2021，38（10）：148-166.

[24] 阿林·杨格，贾根良. 报酬递增与经济进步[J]. 经济社会体制比较， 1996，12（2）：52-57.

[25] 白俊红， 蒋伏心. 协同创新、空间关联与区域创新绩效[J]. 经济研究， 2015，50（7）：174-187.

（责任编辑：陈 井）

Circling-layering Economy of Urban Agglomeration，

Co-innovation and Industrial Upgrading

Chen Congbo¹， Ye Azhong²， Lin Zhuang²

（1. School of Business Administration Anhui University of Finance and Economics， Bengbu 233030， China;

2. School of Economics and Management， Fuzhou University， Fuzhou 350108， China）

Abstract：China urgently needs to achieve economic transformation through innovation-driven industrial upgrading to stand out in global competition and lead a new round of industrial reform. China's industrial upgrading involves the largest population and the most comprehensive industrial structure， but the industrial upgrading presents a significant spatial imbalance. The industrial structure of peripheral cities is weak， and the collaborative ability of innovation subjects within cities is insufficient. With the construction of high-speed railway infrastructure， spatial knowledge spillover has become a catalyst for industrial upgrading. The imbalance of industrial upgrading between peripheral cities and central cities can be remedied by spatial knowledge spillover. Therefore， it is necessary to study the spatial spillover effect of co-innovation on industrial upgrading under the circle structure.

Academics generally believe that innovation is the driving force for industrial upgrading on the premise that the technological progress direction selected by independent innovation and learning activities is consistent with the regional conditions， and the regional industrial upgrading and economic development can be effectively promoted. Meanwhile when technological progress is inconsistent with regional conditions， the increase in the number of innovative achievements can not match the effect of industrial upgrading. In terms of spatial spillovers driving industrial upgrading in neighboring regions， existing studies mainly focus on the impact of industrial transfer and spatial knowledge spillovers on industrial upgrading. As for the spatial impact of industrial transfer， domestic scholars use the “flying-geese model" to explain the industrial transfer and upgrading from developed regions to less developed regions. Some scholars also hold a critical attitude towards the "flying-geese model"， for there are still some improvements. First， it has failed to deeply analyze the differences between the spatial spillover effects of co-innovation of heterogeneous cities on industrial upgrading. For the central cities with the status of “leader goose" and a large number of peripheral cities， the urban heterogeneity of the spatial effects of co-innovation on industrial upgrading remains to be found; second， the dynamic impact of co-innovation space spillover on industrial upgrading is not considered; third， the empirical method mostly adopts a linear spatial model. If the linear assumption of spatial dependency is relaxed， the model setting should be more realistic to obtain more accurate estimation results. Therefore， this paper studies the spatial-temporal effect and urban heterogeneity of industrial upgrading of co-innovation between central cities and peripheral cities in the urban agglomeration circling structure， and then explores why industrial upgrading of central cities is in a dominant position in the circling structure. In terms of demonstration， the dynamic threshold spatial Dubin model is applied for the first time to test the spatial spillover of the co-innovation of the center and peripheral cities on industrial upgrading.

This paper constructs an asymmetric spatial weight matrix based on the Yangtze River Delta Economic Zone panel data from 2009 to 2019 to characterize the spatial relationships of circling-layering economy， and then builds a semi-parametric two-mechanism dynamic spatial Durbin model to investigate the spatial and temporal effects of co-innovation on industrial upgrading and its urban heterogeneity. The findings are as follows： （1） the Yangtze River Delta Economic Zone industrial upgrading has significant dynamic and spatial correlation， and the spatial and temporal effects of co-innovation of neighboring cities on industrial upgrading cannot be ignored; （2） cooperative patents of central and peripheral cities can promote the industrial upgrading of neighboring cities in short and long run while the government funding of co-innovation by central cities is disadvantageous to the industrial upgrading of peripheral cities in long run; （3） the current effect of co-innovation on industrial upgrading of local cities shows a marginal decreasing trend， and the reason for maintaining the advantage of industrial upgrading of central cities is more likely to come from the spatial spillover of co-innovation from neighboring cities to central cities， rather than the advantages of the central city's own co-innovation. The results are helpful to understand the spatial and temporal effects of co-innovation on industrial upgrading and to promote the integrated development of innovation between central and peripheral cities， and provide practical significance to realize the industrial upgrading of urban agglomerations as a whole.

Key Words：Circling-layering Economy; Co-innovation; Industrial Upgrading; Semi-parametric Two-mechanism Dynamic Spatial Durbin Model