层叠分段傅里叶变换的数字Stretch实现新方法*

林钱强,秦正阳,2,莫璨瑜,2

(1. 国防科技大学 电子科学学院 ATR重点实验室, 湖南 长沙 410073; 2. 西安电子工程研究所, 陕西 西安 710100)

当前,在采用线性调频(linear frequency modulated, LFM)信号的雷达系统中,Stretch(又称Dechirping)处理技术被广泛应用于时延测量[1-2]、抗干扰处理[3-4]、参数估计[5]、宽带信号脉冲压缩[6-7]等领域,有效降低了雷达接收机的信号采样率和后端信号处理的数据率。然而模拟域的Stretch处理方法也存在诸多问题,如在宽带高分辨雷达中,模拟域的Stretch处理方法带来系统失真移变、高精度大带宽线性调频参考信号产生困难以及回波处理后蜕化为非相参信号等问题[8-12],使得Stretch处理的性能与应用受到限制。文献[13]提出的数字域Stretch处理方法,将中频直接采样得到的目标回波信号与数字化的参考信号作差频处理,再通过抗混叠低通滤波和数据抽取,最终得到Stretch处理结果。数字域的Stretch方法有效解决了模拟域Stretch存在的问题,得到了广泛的应用[14-15]。然而,在大抽取倍数情况下,特别是当抽取倍数无法分解为两个或多个正整数相乘时,采用数据滤波抽取实现数字Stretch处理的抗混叠低通滤波器将消耗大量硬件资源,这将提高数字Stretch工程应用的门槛。

文献[16]提出了一种将数据分段进行相关运算和抽取滤波以实现高效计算雷达模糊函数的方法。受其启发,本文通过分析数字Stretch处理的数字滤波与数据抽取原理,并结合快速傅里叶变换(fast Fourier transform, FFT)运算的特性,提出一种利用层叠分段FFT运算的数字Stretch处理工程实现新方法,并用实测数据对其有效性进行了验证。

1 FFT运算的等效滤波原理

雷达中频回波信号经过数字Stretch处理中的数字混频后,其带宽比原始发射信号的调频带宽要小得多,因此信号存在过采样。为了降低后续信号处理以及数据存储的压力,应当对数字混频后的数据进行抽取。为了避免数据抽取过程中产生频谱混叠,在对数据进行抽取之前,必须先用抗混叠滤波器对信号进行滤波。

以x(n)(n=0,1,…,N)表示回波信号与参考信号数字混频后的差频信号序列,h(m)(mK=0,1,…,K-1)表示K-1阶滤波器,则差频信号序列的滤波输出序列为:

构造由K个滤波器组成的复调制滤波器组[17]。

k=0,1,…,K-1

(2)

令

(3)

(4)

而对于复调制滤波器组hk(m),文献[18]分析了其中各个滤波器的频率响应特性:各滤波器具有线性相位,幅度特性为sinc(x)形状,而幅频响应的主瓣中心频率位于fc=kfs/K处,主瓣宽度为fs/K,第一旁瓣高度约为-13.2 dB。因此hk(m)可以看成是以K-1阶积分梳状滤波器(cascade integrator comb filter, CICF)为原型低通滤波器构造的复调制滤波器组,各滤波器的频率响应相当于CICF的频率响应以fs/K为步进长度沿频率轴滑动。显然,第0通道的滤波器即为通带频率为fs/(2K)、阻带衰减为13.2 dB的K-1阶低通滤波器。

2 序列抽取及层叠分段处理

为了减轻后续信号处理以及数据存储的压力,低通滤波后所得序列需要进行抽取。数据抽取的倍数记为D,若数据序列长度为N,D可以适当取值使得N/D为整数,记为I,则式(4)中的输出序列经D倍抽取后可表示为:

i=0,1,…,I-1

(5)

如果令K=D,则式(5)进一步化为:

(6)

通过上述分析可知,数字Stretch混频后的数据低通滤波与抽取处理可以用数据的分段FFT运算并对结果进行抽取来实现,数据分段的长度亦即FFT运算的点数等于数据的抽取倍数D。假设x(n)分为I段子序列xi(n)(i=0,1,…,I-1),每一段子序列的FFT运算所得的序列表示为:

Xi(k)=FFT[xi(n)]

(7)

则低通滤波再抽取后的数据序列y′0(i)表示为:

y′0(i)=Xi(k)|k=0

(8)

由第1节分析可知,复调制滤波器组hk(m)的旁瓣都比较高,即滤波器的阻带衰减一般情况下无法满足工程需求,同时对x(n)的分段FFT运算也会造成一定程度的频谱泄漏和混叠失真[18]。通常情况下可通过改变低通原型滤波器重新构造复调制滤波器组以提高利用FFT运算进行滤波的性能。假设低通原型滤波器的单位取样响应为h(m),则重新构造复调制滤波器组为:

(9)

将其代入式(6)并注意到式(1)中h(m)需经过序列反向操作,于是化简后可得:

令xi(m)=x(iD-D+1+m)h(D-1-m),式(10)可化为:

(11)

式(10)可以视为对子序列加窗后再进行FFT运算。可以看出,D点的FFT运算要求h(m)的阶数为D-1,当D较小时一般很难设计出通带阻带性能都比较好的低通原型滤波器。例如,中频回波信号的采样率为2.4 GS/s,数字Stretch混频后的数据抽取倍数为100,所需低通滤波器的通带截止频率为5 MHz,阻带起始频率为7 MHz,采用等纹波法与窗函数法设计的低通原型滤波器的幅频响应分别如图1中虚线与点划线所示。由图1可见,在阶数为99的约束下,等纹波法设计的低通原型滤波器的阻带衰减始终只有十几分贝,且无法保证平坦的通带特性;而采用窗函数法(图1中采用汉明窗进行设计)虽然可以得到较大的阻带衰减,但过渡带却远远无法满足设计要求,更容易造成带外信号的混叠,引起混叠失真。显然要想设计出性能较好的低通原型滤波器,必须适当增大滤波器的阶数。图1中实线所示的滤波器幅频特性即为采用汉明窗设计的1 999阶低通原型滤波器,具有较好的通带平坦度与阻带衰减性能。

图1 低通原型滤波器幅频响应对比Fig.1 Comparison of amplitude frequency response of low pass prototype filters

然而增加原型滤波器的阶数意味着式(11)中FFT运算点数也将增大,必将增加运算量,同时原先的数据序列分段FFT运算的方法也不再适用。由于FFT运算点数增加,新的调制滤波器组中的滤波器个数也相应增加,各滤波器的主瓣中心频率也相应改变,导致滤波器通带之间存在重叠,而由上一小节讨论的结论可知,对数据序列的低通滤波只需取第0通道的滤波结果即可。因此可在保证第0通道输出结果不变的情况下,对FFT运算结果进行频域抽取。仍然假设低通原型滤波器的阶数为K-1,FFT运算的点数为K。取K为D的整数倍,频域抽取的倍数设为L=K/D,代入式(11)可得:

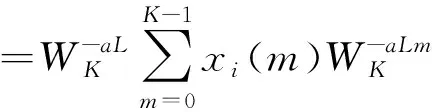
a=0,1,…,D-1

(12)

h(LD-1-pD-q)]

(13)

则式(12)可以看成序列x′i(q)的D点FFT运算,其结果记为X′i(k),而对于所求的第i时刻低通滤波器的输出则应取X′i(0),由此组成的新序列y″0(i)(i=0,1,…,I-1)即为数字Stretch混频后滤波抽取的结果。式(12)通过对输入数据序列加窗并重新组合,在不增加FFT运算点数的情况下,只增加了少量的加法运算,改善了低通原型滤波器的通带与阻带性能。对于整个数字混频后的数据序列,仍分成I段子序列,每一段子序列长度为K,各段数据序列之间存在重叠部分,第i段数据为x(iD+m)(m=0,1,…,K-1)。对于iD+m(i=0,1,…,I-1;m=0,1,…,K-1)取值超过输入序列长度时,可进行补零处理。图2给出数据序列x(n)的层叠分段示意图,式(12)的数据运算原理如图3所示。

图2 数据层叠分段示意图Fig.2 Schematic diagram of data cascading segmented

图3 序列层叠分段FFT实现信号的低通滤波与抽取(第i段)Fig.3 Low pass filtering and decimation of signals using sequential cascading segmented FFT (Segment ith)

采用层叠分段FFT运算实现信号的滤波与抽取之后,对所得的新序列再进行FFT运算,即可得到数字Stretch处理的最终结果。至此,可以总结得出层叠分段FFT运算实现数字Stretch处理的步骤如下:

1)根据数字混频后数据抽取与所需低通原型滤波器的通带阻带特性要求,选择合适的数据抽取倍数D与分段长度K,使数据点数N可以被D整除,且K为D的整数倍,记I=N/D;

2)以窗函数法设计K-1阶低通原型滤波器h(m),根据图2以及式(12),对输入序列x(n)分段并利用h(m)对其加窗;

3)根据式(11)依次对各段加窗后的数据重新组合并计算D点FFT,第i段FFT结果记为Xi(k)(k=0,1,…,D-1),取Xi(0)(i=0,1,…,I-1)组成新的数据序列记为y(i)(i=0,1,…,I-1);

4)对序列y(i)做I点的FFT运算,可得数字Stretch处理的结果。

3 算法验证与分析

3.1 算法验证

雷达目标回波信号经Stretch处理后,将目标的位置信息映射为频率信息。对于理想的点目标而言,其回波信号经Stretch处理后为单点频信号,对该点频信号进行FFT处理即可得目标一维距离像,测量其主瓣宽度和旁瓣高度是否满足雷达信号参数对应的点目标一维距离像特性,可作为衡量Stretch处理算法正确性的依据。

为了验证本文所提算法的有效性,本小节首先采用仿真的雷达点目标回波信号经过本文算法处理后,做FFT运算,测量其主瓣宽度和旁瓣高度。仿真的目标回波信号主要参数采用地基雷达实验平台的实际参数,如表1所示。

表1 地基雷达实验平台的系统参数Tab.1 Parameters of a ground-based radar experimental system

仿真所得点目标一维距离像如图4所示,其中主瓣宽度(-3 dB处)为0.15 m,旁瓣高度为-13.2 dB(FFT运算时加汉宁窗),可知本文算法处理结果是正确的,验证了算法的可行性。

图4 本文算法处理所得点目标一维距离像Fig.4 Range profile of a point target processed by this algorithm

为了进一步验证算法的有效性,采用匹配滤波与本文算法分别对外场实测数据处理后进行对比。实测数据录取于某地基雷达实验平台,系统主要参数已在表1给出。

目标的单次中频回波直接采样后经过数字正交解调得到I、Q两路复信号,其复采样率为1.2 GS/s,则可得数据点数为1.2 GS/s×202 μs=242 400。数字Stretch参考信号时宽与采样波门时宽保持一致,调频斜率与发射信号保持一致。经计算可知Stretch处理后信号的最大带宽为10 MHz,则理想的数据抽取倍数为120。考虑到实际低通滤波器的可实现性,这里选择抽取倍数为100。层叠分段FFT处理中每段子序列长度为2 000点,采用1 999阶汉明窗对带外信号进行抑制。层叠分段FFT处理中的FFT运算点数均等于数字抽取倍数即100点。图5显示的是采用多级滤波器级联与基于层叠分段FFT的数字Stretch处理方法所得到的某一帧数据的一维距离像(图中横坐标以观测窗口起始为0 m)。从图5中可以看出,基于层叠分段FFT算法的数字Stretch方法能够正确对回波信号进行脉冲压缩,得到与多级滤波器级联方法一样的一维距离像结果,验证了本文算法的可行性。

图5 分别采用多级滤波器级联抽取与层叠分段FFT处理得到的一维距离像Fig.5 Range profile obtained by cascading decimate with multistage filters and cascading segmented FFT

3.2 资源消耗分析

本小节进一步分析在满足相同数字Stretch处理性能的情况下,采用层叠分段FFT运算方法与采用多级滤波器级联方法的硬件资源消耗。对于表1信号参数,选取两种实现方法的抽取倍数均为100,综合滤波器参数均设定为:通带截止频率为5 MHz,阻带起始频率为7 MHz,通带纹波为0.000 25 dB,阻带衰减为75 dB。

多级滤波抽取处理方法实现数字Stretch处理一般采用级联CICF、半带滤波器(half band filter,HBF)与有限冲击响应(finite impulse response,FIR)滤波器的滤波抽取处理实现结构。抽取倍数分解为5×22×5,则CICF的抽取倍数为5,采用5级级联CICF来提高旁瓣抑制能力,HBF的抽取倍数再分解为两个2倍抽取,最后一级用FIR滤波器来实现5倍数据抽取的抗混叠滤波器,其阶数为150。上述抽取滤波器采用Xilinx IP核实现,利用该滤波器组对数字混频后的信号进行滤波抽取,再对抽取后的数据以汉明窗加权实现旁瓣抑制,并做FFT运算(抽取后数据序列长度为2 424点,采用Xilinx的FFT IP核来实现FFT运算,应选4 096点的FFT IP核),即完成数字Stretch脉冲压缩处理,可得一维距离像结果。采用上述方案实现数字混频后信号的滤波与抽取所需消耗的主要硬件资源估算如表2所示。

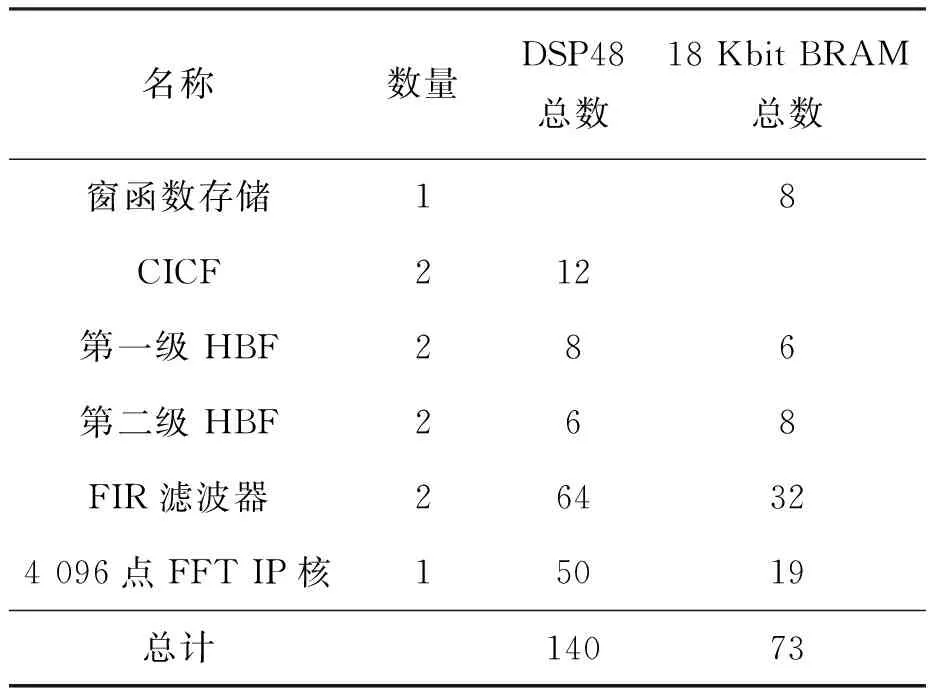
表2 多级滤波器级联实现时的主要硬件资源消耗估算Tab.2 Estimation of main hardware resource consumption in implementation by multistage filers cascading

当采用层叠分段FFT运算实现数字混频后信号的滤波与抽取时,根据第1节的分析可知,同时满足滤波器系数个数为抽取倍数整数倍的要求,选择原型滤波器的阶数为1 999,即分段数据长度为2 000点,窗函数系数即为原型滤波器系数,即2 000个。将解调后的数据序列分成2 424段,长度不足时补零代替。信号滤波抽取完成后,仍采用汉明窗进行旁瓣抑制。该方法完成数字Stretch处理需要进行100点与2 424点两种DFT运算单元,采用Xilinx IP核实现时,应分别选择128点与4 096点的FFT IP核。目标回波的基带数据根据式(10)重新组合后送入FFT IP核进行运算,由于每次只需FFT运算结果的第一个值,因此可在IP核输出第一个值后对IP核进行复位进入下一个128点FFT运算,以此提高运算效率,保证在雷达两个宽带采样波门之间的时间段内完成2 424次128点FFT运算。同样估算实现上述信号的滤波与抽取算法所需的主要硬件资源如表3所示。

表3 分段重叠FFT运算的主要硬件资源消耗估算Tab.3 Estimation of main hardware resource consumption in implementation by cascading segmented FFT algorithm

对比表2与表3的资源消耗并结合3.1节的分析可知,在满足相同数字Stretch处理性能的情况下,采用多级滤波抽取处理方法所消耗的硬件资源约为采用层叠分段FFT运算方法的两倍,由此可见层叠分段FFT运算方法实现数字Stretch处理可以有效降低硬件资源开销,进一步验证了本文算法的有效性。

4 结论

数字Stretch处理在大抽取倍数情况下,特别是当抽取倍数无法分解为两个或多个正整数相乘时,抗混叠滤波器将消耗较多的硬件资源,限制了该技术的工程应用。本文详细分析了数字Stretch处理的数字滤波与数据抽取原理,结合FFT运算的特性,提出了基于层叠分段FFT运算的数字Stretch处理新方法。该方法通过将数字混频后的数据序列层叠分段与重组,利用小点数的FFT运算来实现高性能的数据滤波与抽取。实测数据验证与资源消耗分析表明,本文算法是一种行之有效的数字Stretch实现算法,解决了数字Stretch处理在工程实现中硬件资源开销大的难题,可应用于采用宽带LFM信号的高分辨成像雷达接收机、宽带软件化雷达数字前端信号预处理等。

本文所提出的数字Stretch实现算法与传统方法相比可有效降低硬件资源开销,但因为需要对采样数据进行分段、层叠与补零处理,一定程度上增加了控制逻辑的复杂度;另外,数字Stretch处理相对传统模拟Stretch处理带来量化噪声,有待进一步分析其对目标一维距离像的影响。在下一步的工作中,将针对这些方面开展新的研究。