自旋载体中的超紧组合GNSS接收机跟踪环路设计*
谢郁辰,刘瀛翔,陈飞强,王飞雪
(国防科技大学 电子科学学院, 湖南 长沙 410073)
全球导航卫星系统(global navigation satellite system, GNSS)能够提供高精度且连续稳定的位置、导航和时间信息服务,相关应用已普及到各行各业。自旋载体的导航定位,是GNSS的一种典型应用,尤其常见于航空航天器和各类制导武器之中[1-3]。然而,当载体自旋时,随载体旋转的接收天线会在信号载波相位测量值中引入高阶动态,导致传统的卫星导航接收机环路无法进行长时间的相干积分,甚至造成环路失锁,影响定位性能[4-6]。
针对自旋载体接收机中的GNSS信号跟踪问题,学者们进行了许多相关的研究并提出了多种解决方案。文献[7]研究对比了三种用于炮弹中GNSS信号跟踪的方法,分别为射频前端求和方法、波束成形方法和最大增益方法,并且作者在文献[8]中提出了在旋转圆柱载体接收机中利用两个微带天线进行信号连续跟踪的方法,然而相关研究主要针对的是自旋载体引起天线方向图零陷旋转导致信号丢失的问题,而对自旋载体接收机中载波锁相环(phase lock loop,PLL)的动态应力误差论证较少。文献[9]中指出,当自旋载体的转速超过1.85 Hz时,周期性的多普勒频移对载波跟踪环的影响可以忽略,但是其研究的自旋载体的旋转半径较小(77.5 mm),引入的最大多普勒频移并没有超出环路的牵引范围。文献[10]提出了一种旋转解调模块结构,并使用四阶环路用于跟踪自旋载体的载波相位,但是高阶环路导致相应的PLL并不稳定,因此需要控制载体的转速在一个很小的范围之内。文献[11-12]提出并测试了一种简单有效的旋转跟踪环路,但是使用该环路的相位跟踪误差最大为22°,仍有很大的优化空间。同时,为了跟踪自旋载体接收机中高动态信号,上述研究中的信号相干积分时间都较短(1 ms),而延长相干积分时间则很可能导致环路失锁。相干积分时长和自旋载体转速之间的矛盾仍没有得到很好的解决。
另外,惯性导航系统(inertial navigation system,INS)能够提供高精度的载体速度、姿态信息,进而估计接收信号的多普勒频率,对GNSS环路进行辅助,有效减轻PLL的动态应力[13]。相关设计是一种超紧组合(ultra-tight coupling,UTC)结构,在高动态场景中已得到成功应用[14]。虽然文献[15]指出当自旋载体的转速很高时,惯性器件输出的速度、姿态信息的精度将有所下降,但是利用UTC能够为自旋载体接收机信号跟踪及导航定位提供怎样的性能改善仍然值得进行研究分析。
利用导流洞改建的龙抬头无压泄洪洞设计经历过较长时间的前期论证,至今应用已较普遍,当库水位至出口落差达100 m时其运用开启应较为谨慎,因为即便施工质量控制良好,出现局部损坏可能仍较大。以紫坪铺面板坝为例,排除震损情况,导泄结合段环氧砂浆损坏,经修复后,2013年汛期泄洪检查仍有局部空蚀破坏。目前看,高面板坝龙抬头无压泄洪洞设计已近极限状态。
因此,本文针对自旋载体接收机的信号跟踪和导航定位问题进行研究,通过理论分析推导了自旋载体的旋转运动会在载波信号相位中引入两种正弦动态,而传统的跟踪环路无法处理这种信号动态,当转速较高时PLL将失锁。同时,提出了一种用于自旋载体的UTC环路设计方法,能够在自旋载体接收机中保持环路较长相干积分时间(10 ms)的同时,维持信号的稳定跟踪。此外,还对UTC中INS信息辅助速率、自旋载体转速、相干积分时长和信号载波相位误差之间的关系进行了理论推导与仿真分析。
1 信号与卡尔曼滤波模型
1.1 自旋载体接收信号模型
在自旋载体中,旋转中心和接收机的天线相位中心可能并不重合,并且旋转中心也可能随载体运动。假设自旋载体从A地运动到B地,如图1所示,其中点划线为自旋载体质心的运动轨迹,虚线为天线相位中心的旋转轨迹。
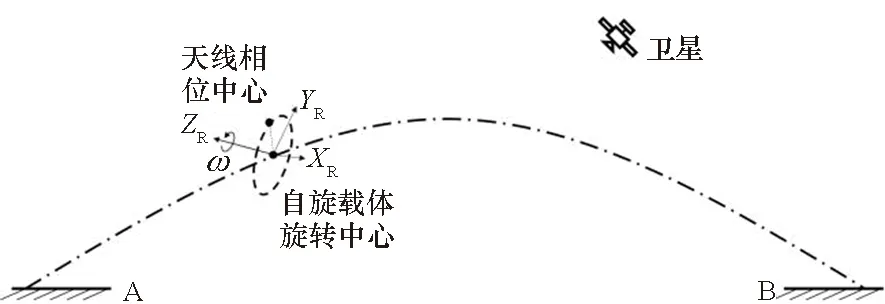
图1 自旋载体的运动轨迹Fig.1 Movement of spinning vehicle
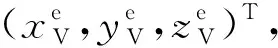
为确定天线相位中心的ECEF坐标,以旋转中心为坐标原点建立旋转坐标系R,其中R系的XOY平面为天线相位中心所在的旋转面,Z轴ZR垂直于其XOY平面,方向与天线旋转的角速度ω相同。R系的X轴与Y轴采用如下方式定义:将天线的旋转面延伸至与ECEF系的XOY平面相交于直线l,在R系的XOY平面中仅有一条直线经过坐标原点且平行于l,选取该直线为R系的X轴XR,并以右手准则确定其Y轴YR。R系三个方向的坐标轴XR、YR、ZR以及坐标原点的相对关系如图1所示。在R系中旋转的天线,其坐标可表示为:
(1)
式中,上标r表示R坐标系,ω为旋转的角速度,t为时间。
患者发现的总趋势是由普查向重点检查发展。进入70年代,美国、荷兰、瑞典、丹麦、加拿大等欧美国家由于反复多次普查,特别是化疗时代疫情明显下降,普查检出率下降,因而在许多国家或地区开始减少用普查,而代之以因症就诊者检查。1970年捷克、挪威、加拿大、荷兰四国得到WHO和IUAT的支持,开展了患者发现方法的研究。证明在一个国家或地区即使开展普查也只能发现新发患者的10%~15%,而绝大多数肺结核是因症就诊发现[1 1]。所以X线普查或集检每发现1例肺结核费用大为提高,同时印度报告,有症状者被动的患者发现极为有效。
由R系到ECEF系的坐标系变换可由两次旋转和一次平移得到,如图2所示。
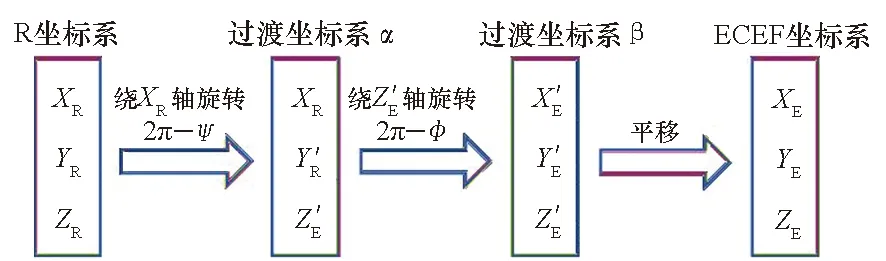
图2 R系到ECEF系的坐标系变换Fig.2 Transformation from R frame to ECEF frame
则旋转天线在ECEF系内的坐标可表示为:
(2)

(3)
(4)
式中:Vk为测量噪声矩阵;Hk为测量矩阵,包含了在测量与状态之间的非线性近似。它们的具体形式也在文献[17]中详细说明。
(5)
ECEF系中从天线指向卫星的向量为:
(6)

节点功能主要是进行CO2及温度的采集,节点是由微控制器模块MCU(Microcontroller Unit)、电源(source)、无线通信模块RF(Radio Freqency)和传感器模块(sensor)组成,其中MCU采用极低功耗的stm8系列单片机作为数据采集器处理单元的核心,并根据需求构建了外围电路;通信模块采用基于WIA-PA技术的无线模块,此模块由中国科学院沈阳自动化研究所自主研发。节点硬件结构图如图2所示。
例如,在教学《人民币的认识》时,掌握1元=10角是本节课的教学重点,为了让学生在情境中体验认识1元=10角,我设计了以下的活动:
(7)

由式(7)可得自旋载体接收机的载波多普勒频率为:
(8)
式中,fl为信号的载波频率,fdop为信号的多普勒频率,c为光速。接收信号的相位θ可以通过信号频率对时间积分得到:
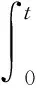
(9)
由式(7)到式(9)可以看出,自旋载体的旋转和运动在接收信号中引入了两种正弦动态,它们不仅与天线的旋转有关,同时还与载体旋转中心的运动有关。
传统的接收机PLL环路通常采用二阶或三阶环路的形式,其中二阶环能稳定无偏跟踪频率阶跃的动态,三阶环能稳定无偏跟踪频率斜升的动态[16]。N阶环路的稳态跟踪误差可以表示为:
(10)

1.2 组合导航卡尔曼滤波模型
GNSS与INS的组合导航,通常使用扩展卡尔曼滤波器(extended Kalman filter,EKF)融合来自两个不同系统的导航信息,并采用误差滤波的方式进行数据处理。
UTC中常用的状态模型为17×1维的向量,分别是3×1维的位置误差δr、速度误差δv、姿态误差δψ、加速度计偏差ba和陀螺仪偏差bg;2×1维的时钟误差bc,包括钟差和钟漂。状态向量可以表示为:
Xk=[δr,δv,δψ,ba,bg,bc]T
(11)
学生恋爱危机的潜伏性和预见性,说明危机可以提前进行预防。做好预防,能够有效地减少危机出现,或者降低危机带来的危害性。班级危机侦察小组要发挥眼睛和耳朵的作用,作为班级的“心理侦察员”,要及时准确的对恋爱征兆信息进行搜集、分析与上报。同时高校应该针对各类恋爱危机事件的发展规律和趋势,编写恋爱危机处理手册,以便发生危机时能更加有序高效地开展工作。有条件的高校还可以组建大学生情感心理工作室,工作室秉承尊重、保密的原则,为被情感困扰的学生排忧解难,降低恋爱危机事件发生的几率。
Xk+1=φkXk+ΓkWk
(12)
式中,Wk为状态的噪声向量,φk为状态转移矩阵,Γk为系统噪声驱动矩阵,其具体表达式较复杂,可参考文献[17]中的详细说明。
若采用误差滤波的方式,则UTC中的测量值为M颗可见卫星由GNSS测量的伪距和伪距率与由INS估计的伪距和伪距率的差值,以单颗卫星为例,有:
(13)
测量方程为:
Zk=HkXk+Vk
(14)
因此由R系到β系的坐标变换矩阵为:
在此次创新战略中,美国首次提出政府层面的服务创新策略,并采取人才、创新思维和技术的结合来提高政府的工作绩效。政府部门的具体创新措施主要包括以下4个方面:一是创建“创新工具包”,改进政府核心服务流程,提高政府解决问题的效率;二是建立政府创新实验室,激发政府部门工作人员的创新能力;三是创建数字服务团队,提升政府部门对美国民众和企业的在线服务质量;四是建立证据机制来推动社会创新。
因此,组合导航的EKF滤波过程可以由五个步骤循环进行[18]。
步骤1:预测先验的状态向量。
(15)
步骤2:计算先验的新息矩阵。
(16)
为简化分析,假设卫星、旋转天线和旋转中心三者共面,几何关系如图7所示,其中r为旋转半径。则LOS方向上的速度为:
对两组患者的护理后的护理总有效率、护理满意度、并发症发生率进行观察,在观察护理满意度这一指标时,主要应用的是百分制问卷调查法,满意:大于85分;较满意:在60~85分之间;不满意:小于85分。护理满意度等于满意与较满意的总人数除以例数。
从各种物性指标来看硬度值越低,嫩度越高[14]。说明犊牛肉的硬度比成年牛肉低,嫩度比成年牛肉高。其中里脊的嫩度最好。这与上面剪切力值的结果是一致的。
Qk-1=E[Γk-1Wk-1·(Γk-1Wk-1)T]
(17)
步骤3:计算EKF滤波增益。
2)市外电源方面,形成了2+X格局:(1)华东电网内的安徽煤电基地,(2)华东电网外的三峡和金沙江等西南水电,并在华东电网内参与建设核电、抽水蓄能等项目。
至臻天文台认证测试采用全自动设备,可24小时运作,对腕表的全面检测需经过283个步骤方可完成。METAS亦设有独立的办公室,以监督检测过程,确保每一枚拥有至臻天文台认证的腕表均达到行业高标准的精准度、防磁性和其它性能。
(18)
对自旋载体接收机的信号特性、UTC跟踪环路性能以及误差特性进行仿真。为简化分析,仿真中假设接收天线随载体在水平面内绕定轴逆时针旋转,载体的高度没有发生改变,则图1所示的三维空间内的运动退化为如图7所示的平面内运动。仿真中GNSS接收机环路采用二阶延迟锁定码环(delay lock loop,DLL)和三阶锁相环的方式,UTC接收机环路采用INS辅助二阶锁相环的方式,仿真中使用的主要参数在表1中列出,为对比不同精度等级的惯性测量单元(inertial measurement units,IMU)对性能的影响,选择为商业级和战术级的惯性器件,其误差特性分别在表2和表3中列出。
(19)
保持PLL环路锁定的典型条件为环路相位误差的3倍不超过45°:
(20)
步骤5:更新EKF新息矩阵,其中I为单位矩阵。
(21)
至此完成EKF滤波,得到各状态的估计值。UTC中使用这些状态量对位置、速度、姿态、加速度计、陀螺仪、时钟进行修正,可以求解并输出最终的导航信息。
2 UTC跟踪环路设计
传统GNSS单系统的接收机结构如图3所示。经射频前端采样后的数据与本地生成的两路正交载波相乘后,再与本地伪码相干积分,得到I、Q两路相干积分结果。经环路鉴相与滤波,接收机通过调整伪码和载波相位的数控振荡器(number controlled oscillator,NCO),控制本地码相位、载波相位与接收信号保持同步。

图3 GNSS单系统接收机结构Fig.3 Structure of GNSS single system receiver receiver
接收机保持相位锁定的关键在于环路NCO的控制。由式(10)可知,N阶环路可以稳定无偏地跟踪N阶的位移动态,但是高阶环路容易发散,工作并不稳定。因此通常接收机的环路不超过三阶,环路滤波器传递如图4所示[16]。

图4 三阶环路滤波器传递框图Fig.4 Transfer structure of 3-order loop filter
环路的系统函数为:
(22)
式中,ωn为环路特征频率,K为环路增益,s表示微分,a3、b3是环路系数。
INS有很高的数据输出率,通常为200~2 000 kHz,能够更及时感觉到载体的动态变化,提供更高精度的速度、姿态信息。因此,如果使用INS提供的动态信息辅助GNSS,则GNSS仅需要维持二阶环路,用于处理环路中INS残留的动态应力误差以及噪声误差。相应的接收机设计如图5所示。

图5 UTC接收机结构Fig.5 Structure of UTC receiver
在UTC跟踪环路中,NCO由INS估计的多普勒频率直接控制,在每次INS数据输出时进行更新。在每个相干积分周期结束进行环路滤波时,INS估计的多普勒频率和环路滤波的结果共同更新NCO,其中环路滤波结果用于修正残留的动态应力误差和噪声误差。UTC环路滤波器的传递框图如图6所示。
状态向量的转移矩阵为:

图6 UTC环路滤波器传递框图Fig.6 Transfer structure of UTC loop filter
由于INS有较高的数据输出速率对环路进行辅助,NCO能够快速更新适应自旋载体的动态。NCO在每次更新时刻到来之前保持不变,这段时间内的相位误差即INS辅助的残留动态应力误差,需要由GNSS环路在每次相干积分结束时由环路滤波进行补偿。当自旋载体转速很高时,残留动态应力误差也会随之增大,同样会造成环路失锁。因此,INS信息辅助速率、载体旋转速度和相干积分时长之间存在制约关系。
其中,Qk-1为状态噪声的协方差阵。

图7 旋转天线与卫星的几何关系Fig.7 Geometrical relationship of spinning antenna and satellite
vLOS=ω·r·sin(ωt)
(23)
因此接收信号的多普勒频率为:
“路”并不是在你脚下的可供行走的道路,而是指一切能够满足宝宝需求的具体做法。归纳起来,可以有以下4个问题:
(24)
假设相干积分的起始时刻为T0,相干积分时长为Tcoh,则一个相干积分周期内,由多普勒频率引起的信号相位变化量为:
(25)
假设INS信息辅助速率为1/Taid,且有Tcoh=NTaid,其中Taid为INS数据输出的周期。 INS在每次输出数据时估计的多普勒频率,在一个Taid周期内保持不变,则INS控制NCO产生的相位变化量为:
(26)
因此,残留的动态应力相位误差为:
θres=θdop-θaid
(27)
步骤4:更新状态向量的预测值。
80年代在中国东部沿海一带的玄武岩中,相继发现了许多蓝宝石矿床。其中以山东(昌乐)蓝宝石质量最佳。晶体呈六方桶状,粒径较大,一般在1cm以上,最大的可达数千克拉。蓝宝石因含铁量高,多呈近于炭黑色的靛蓝色、蓝色、绿色和黄色。以靛蓝色为主。宝石级蓝宝石中包裹体极少,除见黑色固态包体之外,尚可见指纹状包体。没有绢丝状金红石及弥漫状液体包体。蓝宝石中平直色带明显,聚片双晶不发育。大的晶体外缘可见平行六方柱面的生长线。山东蓝宝石因内部缺陷少,属优质蓝宝石。
3σPLL=3σi+θe<45°
(28)
式中,σi为热噪声误差、晶振误差和阿兰方差的均方和,其计算方法可参考文献[16],θe为动态应力误差。由此,可以分析在PLL环路不失锁的条件下,INS信息辅助速率、自旋载体转速以及相干积分时长之间的关系,详细的数值仿真分析在第3节中给出。
3 仿真与分析
其中,Rk为测量噪声的协方差阵。

表1 仿真参数Tab.1 Parameters for simulation

表2 商业级IMU误差特性Tab.2 Error characteristic of commercial IMU

表3 战术级IMU误差特性Tab.3 Error characteristic of tactical IMU
对比自旋接收机与非旋转接收机信号的多普勒频率差异,如图8所示。
从图8中可以看出,非旋转接收机的信号多普勒频率近似缓慢线性变化,这是由卫星运动引起的频率变化。而自旋载体接收机的信号多普勒频率在线性变化的基础上叠加了正弦变化,表现为正弦函数的最大值与最小值缓慢递增。由式(7)和式(8)可知,这种频率变化是由载体旋转引入的LOS方向上的正弦速度产生的,传统接收机的N阶环路设计无法跟踪快速变化的正弦动态,环路将会失锁。
对比传统三阶环路和UTC环路对自旋载体接收机信号的跟踪性能,分别如图9、图10和图11所示。

图9 码相位跟踪误差Fig.9 Code phase error of tracking loop

图10 载波相位跟踪误差Fig.10 Carrier phase error of tracking loop

图11 多普勒频率跟踪误差Fig.11 Frequency error of tracking loop
从图9~11可知,GNSS三阶环路无法跟踪自旋载体接收信号的载波相位,PLL环路失锁且载波相位误差发散,达到104量级;码环的稳健性优于载波环,虽然没有失锁,但是码相位误差较大(最大值约为0.06 chip),且旋转呈现出一定的周期性;由于载体定轴旋转,多普勒频率周期变化,虽然GNSS环路失锁,但是频率误差仍表现出周期性。
UTC环路能够稳定跟踪信号的码相位、载波相位和多普勒频率。使用商业级IMU时,码相位误差基本小于0.025 chip,载波相位误差小于50°,多普勒频率误差基本小于1 Hz;使用战术级IMU能取得更好的性能,码相位误差小于0.01 chip,载波相位误差小于10°,多普勒频率误差小于0.4 Hz。由于载体周期运动,载波相位误差和多普勒频率误差也呈现一定的周期性,但这种周期性在使用消费级IMU时不明显,因为IMU的误差水平较大,噪声误差成为主要成分。三种环路码相位误差、载波相位误差和多普勒频率误差的统计特性对比如表4所示,可以看出:UTC-商业级IMU环路虽然能够保持信号跟踪,但是误差较大,不能够保证高精度的定位;而UTC-战术级IMU对码相位误差的改善程度达到2个数量级,同时能解决载波相位跟踪发散的问题,且对载波相位、多普勒频率都取得了良好的跟踪性能。

表4 跟踪误差统计特性Tab.4 Statistic characteristic of tracking error
传统三阶环路和UTC环路对自旋载体的定位性能对比如图12、图13和图14所示。由于载体没有垂直方向上的运动,图中仅展示水平面内的运动轨迹。

图13 UTC-商业级IMU定位轨迹Fig.13 Position result of UTC-commercial IMU loop

图14 UTC-战术级IMU定位轨迹Fig.14 Position result of UTC-tactic IMU loop
由于GNSS三阶环路无法锁定信号,只能使用码相位跟踪结果定位,从图中可以看出其定位误差逐渐发散,10 s内最大误差超过5 m。UTC环路能够锁定信号载波相位,其定位精度很高,导航解算的轨迹与载体的真实运动轨迹基本重合;且使用战术级IMU的UTC环路定位性能显著优于使用商业级IMU的UTC环路,残留的误差主要来自IMU器件噪声引起的相位误差以及UTC环路更新间隔之内的载体旋转引入的相位误差。位置误差的统计特性如表5所示。
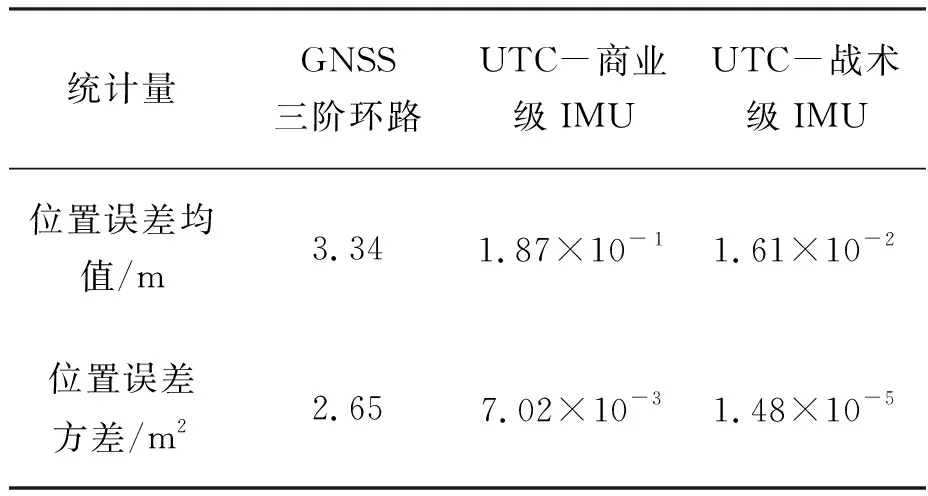
表5 位置误差统计特性Tab.5 Statistic characteristic of position error
通过数值仿真分析式(25)~(28)中INS信息辅助速率、自旋载体转速以及相干积分时长之间的关系。由于相干积分时长与环路输出的信噪比以及定位性能密切相关,在接收机设计时通常希望尽可能延长相干积分时长来提升性能。因此数值仿真中设置相干积分时长为10 ms,主要研究分析INS辅助信息速率与自旋载体转速之间的关系。仿真结果如图15所示。

图15 INS辅助周期与转速的关系Fig.15 Relationship of INS-aid period and angular rate
从图15中可以看出,由设置的仿真参数计算的残留动态应力误差门限约为29.2°。当自旋载体转速增大时,相同INS信息辅助周期Taid的残留动态应力误差有一定程度的振荡,且最大值有增大的趋势。残留动态应力误差的曲线与门限可能有多个交点,且相交后误差可能减小到0。但需要注意的是式(25)~(28)的推导中假设卫星与天线的旋转共面,实际中由于不同卫星与天线的旋转面存在一定夹角,其投影在旋转面上的速度比实际转速更小,且存在一些特殊信号入射角度使得引入的残留动态应力误差为0,但这并不是普遍的现象。因此不同Taid下可以承受的最大转速ωmax应当是曲线与门限的第一次交点,这样才能保证不同卫星在旋转面内的投影速度小于ωmax时残留动态应力误差都不会超过门限,ωmax的理论值如图中黑色标记与箭头所示。由此可以看出,随着Taid减小,INS信息辅助速率加快,UTC能够承受的最大转速逐渐增大,当Taid为1 ms时,理论的最大转速可以为8.31 Hz。
但需要注意的是,式(25)~(28)的理论推导中没有考虑INS的误差。当转速增大时,IMU的测量误差将增大,这部分误差也将作为残留动态应力误差由GNSS二阶环路处理,从而限制UTC环路能够承受的最大转速。更进一步的定量关系将作为下一步的研究内容。
旧学院入口处的建筑顶部,有一个巨大的穹顶,穹顶部分是1887年修建的,与原有的院落型建筑完美地结合在一起,可谓画龙点睛的一笔。穹顶上还有一座镀金雕像,名为“青春”,是苏格兰雕塑家约翰·哈奇森的作品。
4 结论
针对自旋载体中导航信号的跟踪问题展开研究。当载体自旋时,旋转的天线在接收信号的相位中引入高阶动态,导致传统卫星导航接收机环路无法进行长时间的相干积分,甚至造成环路失锁,影响定位性能。
针对此问题,通过建立信号模型,理论分析了载体自旋在信号相位中引入的两种正弦动态的形式,提出了一种用于自旋载体的UTC环路设计方法,对比了所提UTC环路结构与传统GNSS三阶环路的相位跟踪精度与定位性能,并分析了所提UTC环路中INS信息辅助速率、自旋载体转速以及相干积分时长之间的关系,通过数值仿真计算了不同INS信息辅助速率下UTC环路能够承担的最大转速。仿真结果表明,所提UTC环路能够解决自旋载体中的导航信号跟踪问题,显著提升相位跟踪精度和定位性能,并且能够适应较高的旋转速度。INS误差对所提UTC环路能够承受最大转速的定量影响将作为下一步的研究内容。

