适用于GPU处理的长更新周期卫星导航信号载波相位跟踪环路*
肖志斌,鲁祖坤,林红磊,黄 龙
(国防科技大学 电子科学学院, 湖南 长沙 410073)
为提升导航信号测量定位性能并考虑多兼容互操作、军民分离等因素,自1973年美国建设全球定位系统(global positioning system, GPS)以来,卫星导航信号体制就不断演进:最初GPS/北斗等导航系统均采用二进制相移健控/正交相移健控(binary phase shift keying/quadrature phase shift keying, BPSK/QPSK)的调制方式;后来随着导航系统现代化,大量现代化导航信号采用了二进制偏移调制(binary offset carrier, BOC)类[1]调制技术;近年来,随着低轨卫星星座的发展,低轨导航增强系统[2]及新型低轨导航信号[3]应运而生。可以预知,伴随导通融合需求牵引,高中低轨融合导航系统的建设和发展,卫星导航信号体制必然会快速演进,目前已有大量导航通信融合的信号体制设计[4]。
基于图形处理器(graphic processing unit, GPU)+中央处理器(central processing unit, CPU)的软件无线电的导航信号接收机硬件平台相对固定,软件采用开放式架构,非常适用于新体制导航信号接收开发验证、导航信号地面监测站等对功耗不敏感的场景。国内外有不少学者和机构开展了基于GPU的卫星导航信号软件接收机的研究[5-9],但相对而言处理效率较低,如Park[8]采用2块GTX-Titan仅支持16 MHz采样率70多通道GPS L1信号的实时计算,若需要实现对现有所有导航信号包括未来低轨导航信号的接收,其通道数大于300个,同时考虑到抗多径性能,采样率通常需大于20 MHz,这需要10块GTX-Titan才能实现,处理规模巨大。
GPU并行计算性能与线程并发度和数据交互频度相关,单次处理数据量越大,线程并发程度越高,与CPU之间数据交互频度也越低,并行计算效率越高。常规导航信号跟踪环路通常采用1 ms的环路更新间隔,并行计算效率相对较低。为进一步提高GPU处理效率,需要提高环路更新间隔,若环路更新间隔提升至100 ms量级,则GPU并行计算效率可大幅提升。而传统数字锁相环设计中,要求环路带宽B与环路更新周期T的乘积接近于0,T为100 ms量级时,环路基本无法稳定跟踪[10-11]。在弱信号跟踪场景中通常会通过频率辅助等方式提高积分时间,进而提升跟踪性能[12-13]。但上述方法很难适应高动态的场景,通常需要惯导辅助[14],若没有惯导加速度等辅助信息,大多普勒变化率会导致积分时间内输入信号与本地载波不匹配,造成较大损耗,导致跟踪出现较大误差甚至环路无法锁定。
针对上述背景,提出了一种可适应高动态场景的长更新周期载波相位跟踪环路,该环路从以下两个方面提高长更新周期下的动态适应性:在跟踪初始阶段研究设计一种低复杂度线性调频信号估计算法,实现对多普勒变化率初始精细估计进而压缩信号初始动态,估计性能接近克拉美罗下界(Cramer-Rao lower bound,CRLB),计算复杂度优于目前普遍采用的分数阶傅里叶变换搜索[15-16];在跟踪过程中,采用基于信号相位与频率开环估计+4阶卡尔曼闭环跟踪的方式实现对残余相位、多普勒、多普勒一次/二次变化率的跟踪。仿真表明,该环路可在100 ms量级更新周期下实现高动态导航信号载波相位的稳健跟踪,可适应飞机、低轨卫星等大部分高动态场景;另外,由于采用更长的积分时间,其载波相位测量精度要远优于传统3阶锁相环路(phase-locked loop, PLL),且GPU处理效率更高。
1 长更新间隔载波相位跟踪环路算法原理
1.1 跟踪环路架构
传统高动态导航信号载波相位跟踪环路通常采用二阶锁频环辅助三阶锁相环、三状态(相位、多普勒、多普勒变化率)卡尔曼跟踪环路,并采用很短的环路更新周期,通常为1 ms。上述两种传统跟踪方法将信号动态模型均建立为匀加速运动,即认为短时间内加速度恒定,其动态应力主要来自加速度变化。当采用100 ms量级的长更新间隔时,由于加加速度的存在,在环路更新过程中加速度会发生较大变化,传统载波相位跟踪环路会出现较大跟踪误差甚至无法收敛。
根据上述分析,当环路采用100 ms量级的长更新间隔时,信号动态模型需建立为四阶动态模型,跟踪状态包括相位、频率、频率变化率、频率二阶变化率四个参数,该系统模型假设信号的频率二阶变化率为常数。启动跟踪对多普勒、多普勒变化率进行精确估计确定跟踪初值加快跟踪收敛时间,同时跟踪过程中需要对信号相位、多普勒进行开环估计,具体的信号跟踪架构如图1所示(其中信号相位、多普勒、多普勒变化率均为环路更新间隔的中间时刻)。

图1 长更新周期的载波相位跟踪环路Fig.1 Carrier phase tracking loop with long update period
在信号跟踪初始阶段,在信号捕获得到的信号伪码相位和载波多普勒的基础上,对当前时刻信号的多普勒、多普勒变化率进行高精度估计并作为环路跟踪初值。在信号跟踪过程中,信号多普勒变化率已在牵引范围之内,考虑到多普勒变化率估计值会引入较大测量噪声,仅利用信号相位、多普勒估计值驱动卡尔曼滤波,随后利用卡尔曼滤波更新输出的信号相位、多普勒、多普勒变化率生成本地信号剥离伪码和载波相位。
1.2 跟踪初值精估计
在100 ms量级时间长度内,信号加加速度动态通常恒定,此时导航信号可建模成线性调频信号,跟踪初值估计实际上是估计线性调频信号在中间时刻的信号频率、频率变化率。在进行估计前,可根据捕获得到多普勒在更新间隔内的误差范围对导航信号进行短时间的相干累加积分提高信噪比,同时也降低后续估计的复杂度,相干积分时间可取0.25 ms,其可适应的多普勒误差范围高达2 kHz。
相干累加后导航信号模型如下
(1)
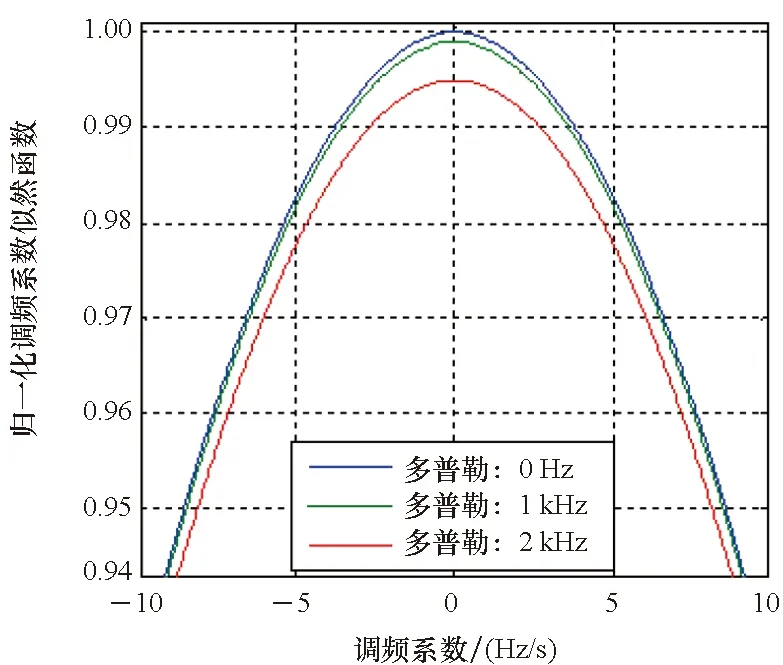
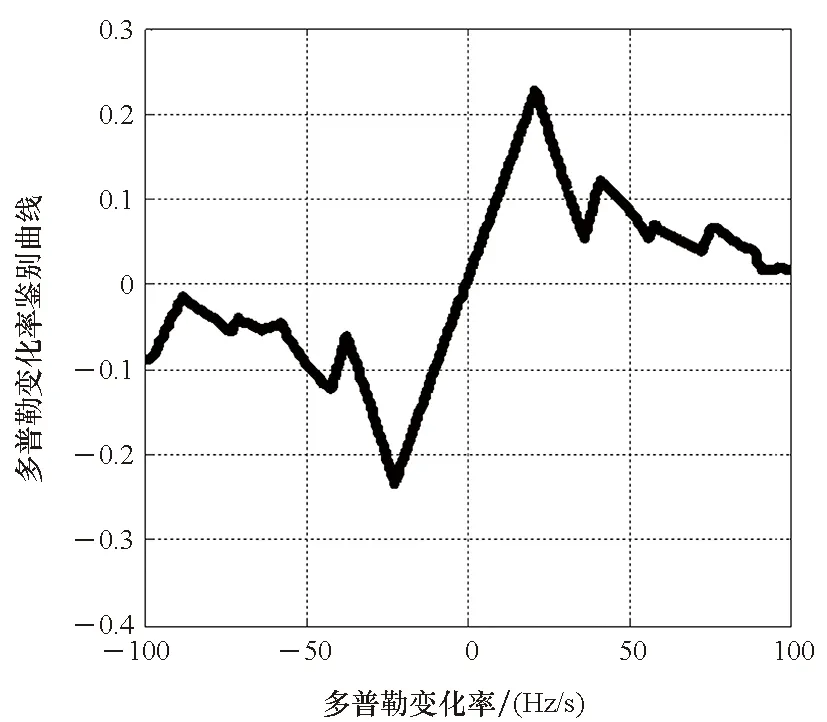
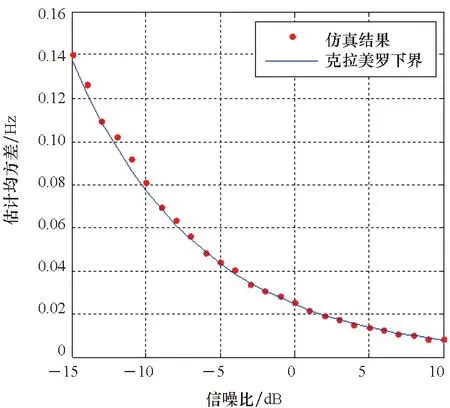
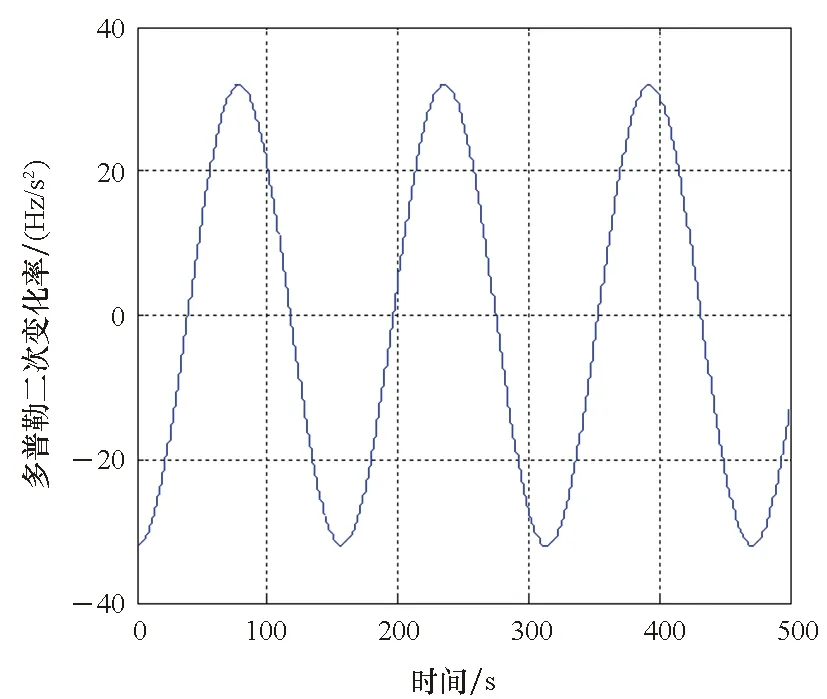
式中:T为信号持续时间,-T/2 s=sI+nI+j(sQ+nQ) (2) 其中:nI、nQ为高斯白噪声,其功率相同记为Pn,sI、sQ为正交信号,两者功率相同记为Ps,其信噪比为 SNRin=Ps/Pn (3) 平方后的信号为 S2=(S2I+jS2Q)+(NI+INQ) (4) (5) NQ=2nInQ+2nIsQ+2nQsI (6) (7) 式(1)所示模型的离散形式为 (8) 其中,Tc为相干积分时间, 0≤n (9) 其中 (10) 对多普勒变化率进行一维搜索,对于给定多普勒变化率搜索值a′,计算不同多普勒下的似然函数最大值 (11) 式(11)右边可以使用FFT近似等效实现,即 (12) 经分析,函数g(a′)表现为左右对称的近似三角函数,且三角峰主瓣宽度近似如式(13)所示(下述关系通过仿真得到)。 W=9.6/T2 (13) 图2~3为采样间隔为0.25 ms,数据点数为1 600,数据时长为400 ms,信号多普勒变化率a=0时,不同中心多普勒情况下归一化的g(a′)曲线(无量纲),显然不同多普勒情况下曲线形状一致,只是幅度有轻微差别,其主瓣宽度约为60 Hz/s。 图2 g(a′)曲线Fig.2 g(a′) curve 图3 g(a′)曲线图(中心局部放大)Fig.3 Partial magnified curve of g(a′) 参考早迟跟踪环,设计多普勒变化率鉴别器,即 (14) 其中:da为鉴别器早迟间隔,可取为g(a′)曲线主瓣宽度的1/4;D(a′,da)为无量纲,经分析D(a′,da)随a′的关系在中心部分近似呈线性。da=15 Hz/s时的鉴别曲线如图4所示。 图4 D(a′,da)与a′的关系Fig.4 Relationship between D(a′,da) and a′ 基于g(a′)及D(a′,da)的上述特性,可以通过多普勒变化率稀疏搜索及插值估计实现多普勒变化率的精确估计,具体方法如下: 1)对多普勒变化率进行间隔为da的稀疏搜索,得到g(n·da),⎣-amax/da」≤n≤「amax/da⎤; (15) (16) (17) 其中 6) 4套690 V 主DP辅助配电板,额定电压为690 V,汇流排额定电流2 929 A,额定短路分断电流54 kA。 (18) 该方法对多普勒变化率进行稀疏搜索,搜索次数少,主要进行FFT运算,FFT运算效率要优于分数阶傅里叶变换,传统线性调频信号参数估计方法通常基于分数阶傅里叶变换。 1.3.1 离散动态方程 信号载波卡尔曼模型的离散动态方程可以写为 δXk=Φ·δXk-1+wk (19) 信号载波状态转移矩阵为 (20) 其中,T为卡尔曼滤波更新间隔。 对于功率谱密度为q的白噪声,记其时域波形为w,则:q=E[w]2,对该白噪声分别进行1~3次积分得到的波形分别为 (21) (22) (23) (24) (25) (26) (27) (28) 接收机晶振的相位和频率噪声qb和qd可以通过h参数求得,具体为 qb=h0/2 (29) qd=2·π2·h-2 (30) 表1给出了接收机中常用的温补晶振(temperature compensate X′tal oscillator, TCXO)和恒温晶振(oven controlled X′tal oscillator, OCXO)的典型h参数。 表1 TCXO和OCXO晶振的h参数Tab.1 h parameter of TCXO and OCXO crystal oscillator 对于采用温补晶振的接收机,当环路更新间隔为100 ms时,可以算得晶振相位噪声对L1频点(fRf=1 575.42 MHz)引入的载波相位和多普勒抖动分别高达0.228周和0.086 Hz,误差太大。而对于采用恒温晶振的接收机,当环路更新间隔为100 ms时,可以算得晶振相位噪声对L1频点(fRf=1 575.42 MHz)引入的载波相位和多普勒抖动分别为0.000 2周和0.000 4 Hz,误差远低于热噪声。因此,长更新周期的跟踪环路主要应用于恒温晶振的高性能接收机,比如卫星导航信号参考站接收机,不适用于采用温补晶振的接收机,如普通导航型接收机。 1.3.2 量测方程 本算法的观测量为当前更新间隔中间时刻的信号残余载波相位Δθ和残余多普勒Δf,估计所采用的数据为更新间隔内的每1 ms相关累加值。在跟踪阶段多普勒变化率残余量较小,考虑到多普勒变化率本身有估计误差,不估计残余多普勒变化率,认为其为0。对于电文已知的导频信号,采用简单的搜索方法可剥离电文,此时每1 ms相关累加值为一单频信号;对于电文位置信号,对每1 ms相关累加值进行复平方即可得到一单频信号。因此,估计过程本质上是对单频信号的频率和相位进行估计,可采用成熟方法[16-17]进行估计。 卡尔曼模型的量测方程为 Yk=Hk·δXk+vk (31) 其中:Yk为观测量,即开环估计得到的当前更新间隔中间时刻的信号残余载波相位和残余多普勒;Hk为测量矩阵;vk为观测量噪声。Yk和Hk分别如下所示 Yk=[Δθ,Δf]T (32) (33) 观测量协方差矩阵为: (34) 其中,σθ,k、σf,k分别为载波相位和多普勒估计误差的方差,方差计算公式见文献[17-18]。 1.3.3 卡尔曼滤波 卡尔曼滤波过程如下: 1)状态向量预测 (35) 2)先验协方差矩阵计算 (36) 3)Kalman增益计算 (37) 4)状态向量修正 (38) 5)后验协方差矩阵计算 (39) 长更新周期面临的主要挑战是高动态条件下的稳健跟踪,主要通过下述三个方面改善动态信号跟踪性能: 1)采用一种低复杂度多普勒变化率估计方法实现对信号多普勒变化率的高精度初始估计,将跟踪初始残余多普勒变化率控制在较小的范围内。 2)采用4阶卡尔曼滤波实现对残余多普勒、多普勒变化率的跟踪。高动态条件下信号存在加加速度,由于跟踪估计的迟滞性,长更新周期下跟踪收敛过程中信号加速度会发生变化,因此传统3阶卡尔曼滤波环路跟踪会不稳定。 3)跟踪过程中采用成熟的单频信号参数估计方法实现对信号相位和多普勒的开环无偏估计,估计精度接近克拉美罗下界,相对于传统鉴频鉴相算法精度更高,跟踪牵引性能更好。传统鉴频鉴相方法线性区间有限,当高动态导致跟踪频率及相位误差较大时,其估计是有偏的,会影响环路收敛。 其具体的动态跟踪性能较难给出理论定量的分析结果,后续章节将通过仿真分析其动态跟踪性能。 2.1.1 估计精度 多普勒变化率的估计克拉美罗下界[19]为 (40) 数据中间时刻的多普勒估计等效于对多普勒变化率估计补偿后得到的单频信号进行估计,其估计可等效于传统的单频信号估计,估计精度的克拉美罗下界[17]可表示为 (41) 仿真时采用4 kHz的数据(相当于相干累加时间为0.25 ms),数据点数为1 600,数据总长度为400 ms,鉴别器早迟间隔为15 Hz/s。线性调频信号真实参数为f=100 Hz,a=100 Hz/s。通过蒙特卡罗仿真这组参数下不同信号信噪比下参数估计精度,每个信噪比场景下蒙特卡罗仿真次数为1 000次,仿真结果如图5、图6所示。显然估计性能接近克拉美罗下界。 图5 多普勒变化率估计精度仿真结果Fig.5 Simulation results of Doppler rate of change estimation accuracy 图6 多普勒估计精度仿真Fig.6 Simulation results of Doppler estimation accuracy 上述分析基于相关累加后的信号信噪比,导航信号通常用载噪比衡量,相关累加值为Ta=0.25 ms时,相关累加后的信噪比与载噪比的关系为 Snr=Cnr-36 (42) 另外,相关累加时由于有多普勒的存在会有额外损耗,损耗为20lg[sinc(πfdTa)],当估计时长内多普勒残余不超过600 Hz时,损耗很小,小于0.3 dB,分析时可不考虑其影响。 当信号存在未知电文时,需要对信号进行复平方,平方后信噪比与平方前信噪比关系如式(7)所示,平方后多普勒和多普勒变化率估计精度仿真结果如图7、图8所示。图中克拉美罗下界是根据平方后信噪比计算并换算为载噪比。 图7 多普勒变化率估计精度仿真结果(存在平方损耗)Fig.7 Simulation results of doppler rate of change estimation accuracy(exists square loss) 图8 多普勒估计精度仿真(存在平方损耗)Fig.8 Simulation results of Doppler estimation accuracy(exists square loss) 2.1.2 计算复杂度 算法对多普勒变化率搜索间隔为9.6/T2,当采样间隔为1/4 ms,数据点数为800(对应数据时长T=200 ms),多普勒变化率搜索间隔为240 Hz/s,最大多普勒变化率为1 000 Hz/s时,仅需要搜索9次,即仅需要做9次FFT运算,且估计精度可达克拉美罗下界。 而目前广泛采用的基于分数阶傅里叶变换的线性调频系数估计算法要达到接近克拉美罗下界的估计精度需要进行几百上千次的搜索(尤其是高信噪比时,调频系数搜索间隔要更小)[15],且分数阶傅里叶变换的计算复杂度要高于FFT,另外GPU中有高度优化的FFT运算库,计算效率更高。因此所提出的线性调频信号参数估计方法计算复杂度低,效率更高。 仿真环路更新间隔取200 ms,主要分析电文已知导频信号的跟踪性能,具体包括动态性能、收敛时间、跟踪灵敏度、测量精度,对于电文未知信号,会存在平方损耗导致信噪比下降,性能下降量可直接根据平方损耗计算得到,具体平方后信噪比如式(7)所示。 2.2.1 动态性能 算法跟踪状态包括相位、频率、频率变化率(加速度)、频率二次变化率(加加速度),其动态应力误差主要来自频率三次变化率的波动。动态场景设计为加速度最大值为800 Hz/s(可覆盖飞机、低轨卫星等大部分动态场景),加加速度可变的正弦运动场景,信号载噪比为40 dB-Hz,主要分析该场景下稳定跟踪所能容忍的最大加加速度。图9、图10为最大加加速度为32 Hz/s2时的多普勒和多普勒变化曲线。 图9 加加速度变化曲线Fig.9 Curve of the jerk change 图10 加速度变化曲线Fig.10 Curve of the acceleration change 分析结果表明,载波相位、多普勒动态应力误差随最大加加速度增大而增大,在当前正弦仿真场景下,稳定跟踪所能容忍的最大加加速度约为64 Hz/s2。图11、图12为不同最大加加速度下的多普勒和载波相位测量误差,其中载波相位测量结果可直接采用开环估计的结果,精度已比较高,动态应力较小,多普勒在大加加速度情况下会存在较大动态应力误差。 图11 不同加加速度下的多普勒测量误差Fig.11 Doppler measurement error under different jerk 2.2.2 收敛时间 采用提出的低复杂度线性调频信号参数估计方法对跟踪初值进行精确估计,可极大加速收敛时间。这里主要比较分析跟踪初值精确估计(使用200 ms数据)和未精确估计情况下的收敛时间,仿真场景与动态性能仿真场景一致,采用加速度为800 Hz/s,加加速度为8 Hz/s2的正弦场景。图13为其比对结果,显然经过跟踪初值精确估计后,初始跟踪载波相位立刻即可收敛,而跟踪初值未精确估计直接进入跟踪时载波相位需要约5 s才能收敛。 2.2.3 跟踪灵敏度及测量精度 仿真场景与动态性能仿真场景一致,采用下述两个场景: 场景一:加速度为800 Hz/s,加加速度为64 Hz/s2; 场景二:加速度为800 Hz/s,加加速度为8 Hz/s2。 分析上述两个动态场景下,不同信号载噪比下的跟踪性能与测量精度,经分析,场景一跟踪灵敏度可达23 dB-Hz,场景二跟踪灵敏度可达 21 dB-Hz,图14为两个场景下不同载噪比下的载波相位测量精度,加加速度为64 Hz/s2在低载噪比时精度稍差,是因为有额外的动态应力误差。 图14 不同载噪比下的载波相位测量精度Fig.14 Accuracy of carrier phase measurement under different carrier noise ratio 从上述仿真结果可看出,所提算法可在大更新周期下实现低信噪比高动态情况下的载波相位高精度稳健跟踪,可实现多普勒变化率及二次变化率分别达800 Hz/s2、64 Hz/s2正弦运动场景下载波相位的稳定跟踪,且跟踪灵敏度低至23 dB-Hz,当载噪比大于30 dB-Hz时,载波相位测量精度优于0.01周。另外,利用提出的低复杂度线性调频信号参数估计方法确定跟踪初值,可实现跟踪的快速收敛,只需要1次环路更新即可实现载波相位的跟踪收敛。 传统高动态跟踪算法通常采用3阶PLL环路或者3阶卡尔曼滤波实现,3阶PLL环路在最优带宽下性能与3阶卡尔曼滤波性能一致。本小节主要以3阶PLL环路的载波相位跟踪精度为参考进行比对分析。 3阶PLL环路主要的误差为热噪声、动态应力误差和相位噪声。根据前文分析采用恒温晶振时引入载波相位测量误差很小,这里对比分析暂不考虑相位噪声。 3阶PLL环路热噪声引入误差(单位为(°))[20]为 (43) 其中,T为环路更新时间,CN0为信号载噪比,Bn为环路带宽。 传统3阶PLL环路为保证跟踪稳定,要求BnT远小于1,在高动态场景下通常选用1 ms的更新间隔。 3阶PLL环路引入的动态应力误差(单位为(°))[20]为 (44) 其中,J为冲击动态。 在给定积分时间T与冲击动态J时,对环路带宽进行遍历,选择最优的环路带宽使得PLL测量误差最小,即可得到3阶PLL环路的最优估计精度。 当冲击动态为64 Hz/s2时,通过数值仿真可得到不同载噪比下的3阶PLL环路跟踪误差,与本文算法的仿真结果比对如图15所示。 图15 本文算法与3阶PLL环路载波相位跟踪精度对比Fig.15 Comparison of carrier phase tracking accuracy between the proposed algorithm and the third-order PLL loop 显然本文算法载波相位跟踪精度远优于传统3阶PLL环路(最优环路带宽下)。 GPU采用大规模线程进行并行计算,单次处理数据量越大,同时处理线程数越多,并行计算效率也就越高。传统3阶PLL环路采用短的环路更新间隔,通常为1 ms,本文算法可实现100 ms量级的环路更新间隔,单次处理数据量大,GPU并行计算效率更高。为分析算法在GPU平台的实现效率,采用Tesla V100高性能GPU平台实现了此算法和3阶PLL环路算法(数据采样率为25 MHz),并比对分析了两者的计算效率,表2给出了更新间隔分别为1 ms(3阶PLL环路)和200 ms(本文算法)时GPU所能实时处理的通道数,显然本文算法的处理通道数要远大于1 ms更新间隔下的3阶PLL环路。 表2 两种算法下所能实时处理的通道数Tab.2 Number of channels that can be processed in real time under two algorithms 针对短环路更新间隔下GPU处理效率受限而长更新间隔下传统跟踪环路在高动态场景下不稳健的这一矛盾,本文提出了一种长更新间隔的高动态载波相位跟踪算法。该算法采用载波相位和多普勒开环估计+4阶卡尔曼闭环跟踪的方式,可实现低信噪比高动态情况下载波相位的高精度跟踪。经仿真验证,在200 ms环路更新间隔下,该算法可实现多普勒变化率与二次变化率分别达800 Hz/s、64 Hz/s2正弦运动场景下载波相位的稳定跟踪,跟踪灵敏度低至23 dB-Hz,可适应飞机、低轨卫星等大部分高动态场景。同时为加快环路收敛,提出了一种低复杂度线性调频信号参数估计算法对信号多普勒及变化率进行精确估计,精度接近克拉美罗下界,且计算效率比传统基于分数傅里叶变换的方法高,利用该算法确定跟踪初值可实现跟踪快速收敛,只需要1次环路更新即可实现载波相位跟踪收敛。由于可以采用更长的相干积分时间、更长的更新周期,本算法载波相位跟踪精度要远优于传统3阶PLL环路,且在GPU中处理效率要更高,经评估采用1块Tesla V100即可支持25 MHz采样率1 800个通道的实时处理。因此,本算法非常适用于对测量精度要求高且导航信号接收通道规模大的应用场景,如应用于未来大规模高中低轨导航星座连续观测的地面高精度导航信号参考站接收机。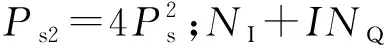



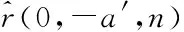




1.3 卡尔曼滤波模型

1.4 算法动态适应性设计分析
2 算法性能仿真验证
2.1 跟踪初值估计性能



2.2 环路跟踪性能



3 与传统3阶PLL环路性能对比
3.1 载波相位跟踪精度对比分析

3.2 GPU实现效率对比分析

4 结论

