挖掘教材资源，促进思维发展——运用一元二次方程解决动点问题

文／王国强

教材中的例习题是教材编写者根据学习目标与内容，反复斟酌，精心设置的，具有很强的代表性和示范性，也是我们学习的重要资源库。

一、原题思考与拓展

（苏科版数学教材九年级上册第28页问题6）如图1，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A出发沿AB以1cm/s 的速度向点B移动；同时，点Q从点B出发沿BC以2cm/s 的速度向点C移动。几秒钟后△DPQ的面积等于28cm2？

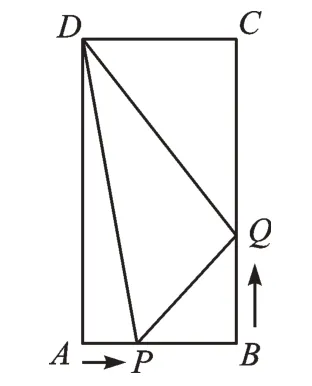
图1

思考1：△DPQ的面积能等于38cm2吗？

思考2：△DPQ的面积有最大值吗？有最小值吗？为什么？

思考3：几秒钟后，△DPQ的面积是△PBQ的面积的3倍？

【思路点拨】我们通过图形特征，发现△DPQ的面积可以用大矩形面积减去三个直角三角形的面积表示，再用面积为38 作为等量关系，列出方程，进而可以在图形的动态变化中思考△DPQ的面积随时间t的变化过程。

拓展：关于△DPQ，你还能提出哪些问题呢？

问题1：几秒钟后△DPQ是等腰三角形？

问题2：几秒钟后△DPQ是直角三角形？

问题3：几秒钟后线段PQ的长等于6cm？

问题4：线段PQ有最大值吗？有最小值吗？为什么？

【思路点拨】矩形ABCD的四个角都是直角，那么图形中存在直角三角形，我们便可在不同的直角三角形中运用勾股定理构造方程解决问题。

对于问题1，我们自然要分类讨论：①PD=PQ，即PD2=PQ2；②QP=QD，即QP2=QD2；③DP=DQ，即DP2=DQ2。

对于问题2，我们也要分类讨论：①∠PDQ=90°，②∠DPQ=90°，③∠PQD=90°。当然，我们通过观察图形特征可以发现，∠PDQ和∠DPQ不可能是直角。

对于问题3，我们要注意动点变化带来的线段变化，利用勾股定理建构一元二次方程求解。

对于问题4，我们要分类思考点P和点Q的动静关系。由速度的2 倍关系联想线段的2 倍长度，不难发现，当点P到B处，点Q到C处时，PQ有最大值。利用勾股定理建构一元二次方程可求出最小值。

【小结提升】化动为静，动的是点，静的是线段长度；数形结合，用含时间的代数式表示图中线段长度；分类讨论，关键是找到临界点。

二、中考链接与迁移

（2023·江苏徐州）如图2，正方形纸片ABCD的边长为4，将它剪去4 个全等的直角三角形，得到四边形EFGH。设AE的长为x，四边形EFGH的面积为y。

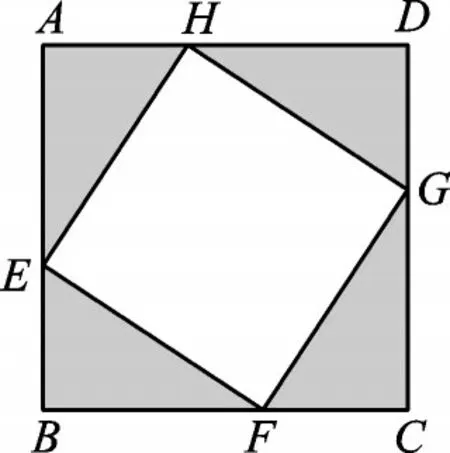
图2

（1）求y关于x的函数表达式；

（2）当AE取何值时，四边形EFGH的面积为10？

（3）四边形EFGH的面积是否存在最小值？若存在，求出最小值；若不存在，请说明理由。

这道中考题的实质和例题很像，只是一个是矩形，一个是勾股弦图。图形在变，不过解题方法却不变，两道题最终都化归为用一元二次方程来解决。

问题1：剪去4 个全等直角三角形，得到的四边形EFGH是什么图形？

问题2：四边形EFGH的面积为10，可否转换成一元二次方程？

问题3：可否用配方法转化四边形EFGH的面积函数表达式？

对于问题1，我们可以借助全等三角形说明图形形状是正方形。

对于问题2，我们先用勾股定理求出动线段长与面积的函数表达式，再化归为一元二次方程来解决。

对于问题3，我们通过配方法转换后，可以在数形结合中用式的特征来解决。